Applied Mathematics
Vol.3 No.12(2012), Article ID:25465,7 pages DOI:10.4236/am.2012.312264
One Common Solution to the Singularity and Perihelion Problems
1Department of Mathematics and Informatics, Faculty of Sciences, University of Novi Sad, Novi Sad, Serbia 2College of Technical Engineering Professional Studies, Čačak, Serbia
Email: saric.b@open.telekom.rs
Received September 18, 2012; revised October 18, 2012; accepted October 25, 2012
Keywords: Celestial Mechanics; Planets; Rings
ABSTRACT
With a view to surmounting the singularity problem on the one hand, as well as the moving perihelion problem of the planets on the other, as two acutely vexed questions within Newton’s gravity concept, the goal of this paper is a modification of Newton’s gravity concept itself.
1. Introduction
It would be difficult to exaggerate the influence of Newton’s theory of gravitation on the subsequent development of physics. As well as explaining Kepler’s laws of planetary motion, Newton’s theory was central to the successful mathematization of physics using the newly-invented calculus and it served as a paradigm for the later theories of electrostatics and magnetostatics. However, new insights into Milky Way satellite galaxies raise awkward questions for cosmologists: Do we have to modify Newton’s theory of gravitation as it fails to explain so many observations? In other words, although Newton’s theory does, in fact, describe the everyday effects of gravity on Earth, things we can see and measure, it is conceivable that we have completely failed to comprehend the actual physics underlying the Newton’s force of gravity. In addition, Newton’s theory does not fully explain the precession of the perihelion of the orbits of the Planets, especially of planet Mercury. Namely, it has been experimentally stated that the perihelion of Mercury’s orbits moves into the plane of its planetary motion around the Sun. In other words, all planetary motions of Sun’s planetary system depart from elliptical orbits obtained from Newton’s gravity theory, [1]. By the strict Schwarzshild-Droste’s solution to the static gravitational field with spherical symmetry, in the general Einstein’s relativity theory, the perihelion problem has been approximately solved, [1]. On the other hand, Einstein’s theory has some difficulties hard to be overcome such as the problem of singularity, that occurs in Newton’s theory too (all relevant physical variables, such as velocity, force, kinetic and potential energy, don’t exist at point of singularity). Accordingly, in order to solve simultaneously these two acutely vexed questions within Newton’s gravity theory, we present, in this research paper, an approximative modification of Newton’s gravity concept itself. The outline of this article is as follows: In the Preliminaries, the space-time continuum (the integral space), as an ambient space, is completely defined. In Section 1 we establish a causal connection between the expression for the kinetic energy of a material point and the Minkowski metric in the four-dimensional space-time continuum. In addition, in two separate subsections of this section we derive Newton’s equations of motion and the relativistic Hamilton-Jacobi equation for a free particle. Since the dynamic (Newton’s) equations of motion are formally derived from geodesic equations in Section 2, this section together with Appendix at the end of the paper provide a possibility of further work on the modification of Newton’s gravity theory in Section 3. In this last section we show that a comprehensive analysis of particle motion under the modified Newton’s gravity force leads to the perihelion motions of a Planet’s elliptical orbit.
2. Preliminaries
By a material point , introduced for the purpose of an useful idealization, one means a geometrical point, which is spatially no dimensional on the one hand and exactly fixed mass on the other. Closely related to the notion of a geometrical point is the set of values
, introduced for the purpose of an useful idealization, one means a geometrical point, which is spatially no dimensional on the one hand and exactly fixed mass on the other. Closely related to the notion of a geometrical point is the set of values 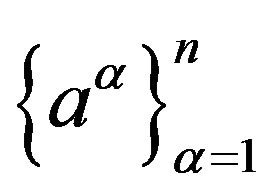 of some arbitrary
of some arbitrary ![]() variables
variables 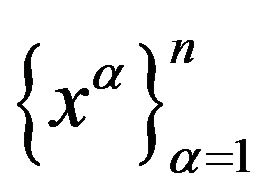 denoting the contravariant co-ordinates of the real
denoting the contravariant co-ordinates of the real ![]() -dimensional configurative space. The geometrical point, defined by a set of zero values
-dimensional configurative space. The geometrical point, defined by a set of zero values , is the zero co-ordinate point. If one of
, is the zero co-ordinate point. If one of ![]() arbitrary variables
arbitrary variables 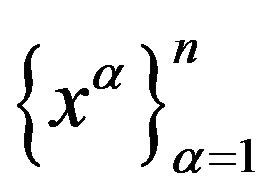 is the time variable
is the time variable , then the space aforementioned becomes the space-time continuum (shortly called the integral space), [2]. As it was noted in [3] the value of
, then the space aforementioned becomes the space-time continuum (shortly called the integral space), [2]. As it was noted in [3] the value of  is called moment or instant.
is called moment or instant.
The set of all geometrical points of the spatial subspace of the integral space, to which the mass ![]() can be joined in some strictly monotonous sequence of permitted instants of the time
can be joined in some strictly monotonous sequence of permitted instants of the time , makes an odograph usually referring to the a trajectory (motion path) of
, makes an odograph usually referring to the a trajectory (motion path) of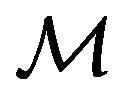 . The time variable
. The time variable  is taken for a unique independent variable, so that all remaining spatial variables
is taken for a unique independent variable, so that all remaining spatial variables 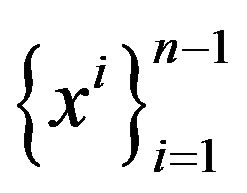 are functional variables. Across all the future text Greek indices take values
are functional variables. Across all the future text Greek indices take values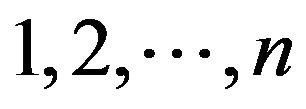 , and Latin ones
, and Latin ones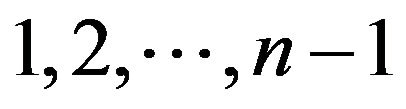 . In the space-time continuum the aforementioned trajectory of
. In the space-time continuum the aforementioned trajectory of 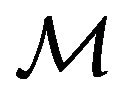 blossoms into an integral curve. The vectors
blossoms into an integral curve. The vectors
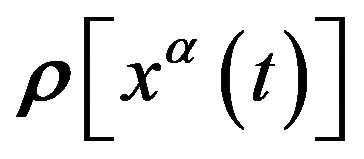 and
and 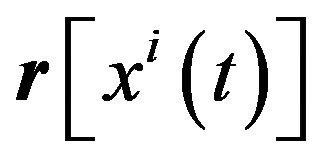 defined with respect to the origin are position vectors of
defined with respect to the origin are position vectors of 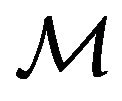 in the space-time continuum and in the spatial subspace of the integral space, respectively. The concept of a vector in vector hyper-dimensional spaces
in the space-time continuum and in the spatial subspace of the integral space, respectively. The concept of a vector in vector hyper-dimensional spaces 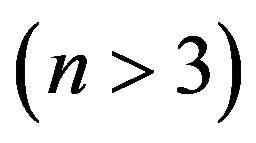 should be conditionally comprehended in the sense of its geometrical presentation in a form of segments. Hence it bears a name linear tensor, [4]. Covariant vectors
should be conditionally comprehended in the sense of its geometrical presentation in a form of segments. Hence it bears a name linear tensor, [4]. Covariant vectors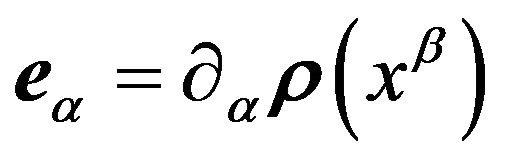 , where
, where 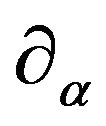
denotes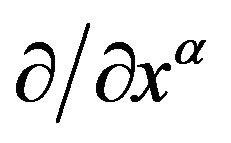 , form a covariant vector basis
, form a covariant vector basis ![]()
of the integral space. The vectors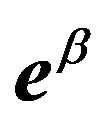 , such that at any point of the space
, such that at any point of the space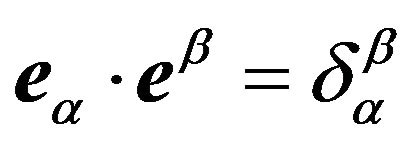 , where the second order system
, where the second order system 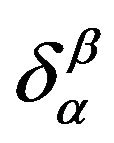 (Kronecker’s delta-symbol, [5]) is the identity
(Kronecker’s delta-symbol, [5]) is the identity ![]() matrix, form a dual basis
matrix, form a dual basis 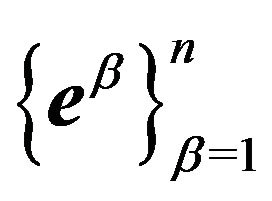 of
of
![]() . The differential
. The differential 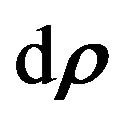 of the position vector
of the position vector 
of  is defined by
is defined by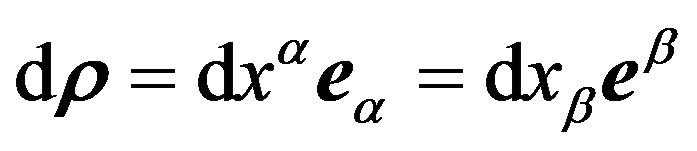 , where the so called Einstein’s convention is applied to a summation with respect to the repetitive indexes (uppers and lowers), herein as well as in the further text of the paper.
, where the so called Einstein’s convention is applied to a summation with respect to the repetitive indexes (uppers and lowers), herein as well as in the further text of the paper.
3. The Action Metric in the Integral Space
Since the integral space is a metric affine space, whose linearly independent basis (fundamental) co-ordinate vectors reduced to the origin form an ![]() -hedral basis, it follows that if
-hedral basis, it follows that if 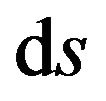 is a line element of the metric affine space of the spatial continuum, then the expression for the kinetic energy
is a line element of the metric affine space of the spatial continuum, then the expression for the kinetic energy ![]() of
of 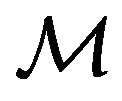 can be stated in more appropriate form:
can be stated in more appropriate form:
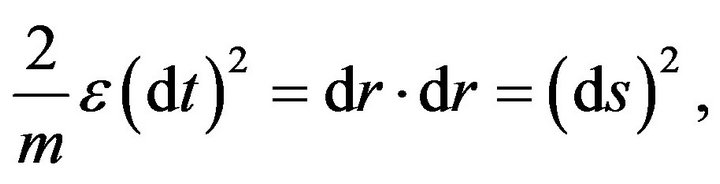 (1)
(1)
considering the fact that the basic mechanical (kinematics and dynamics) parameters of 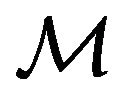 are its velocity
are its velocity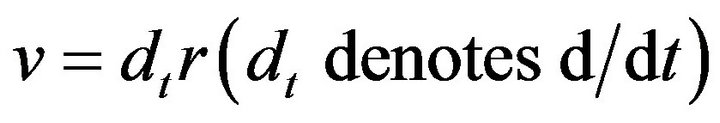 , quantity of motion
, quantity of motion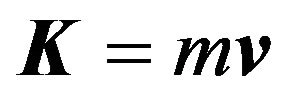 and kinetic energy
and kinetic energy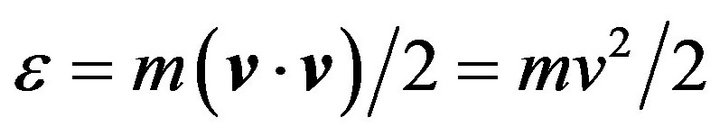 . A term of
. A term of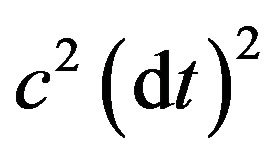 , where
, where ![]() is nominally equal to the light velocity in vacuum, can be added to both sides of the previous equation, as follows
is nominally equal to the light velocity in vacuum, can be added to both sides of the previous equation, as follows
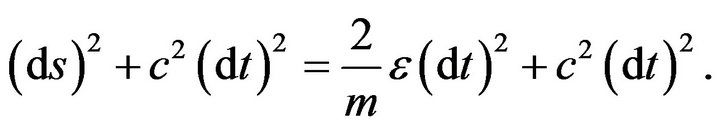 (2)
(2)
For 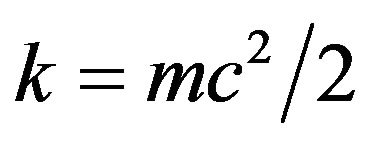 let
let 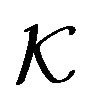 be such that
be such that . Then, (2) becomes
. Then, (2) becomes
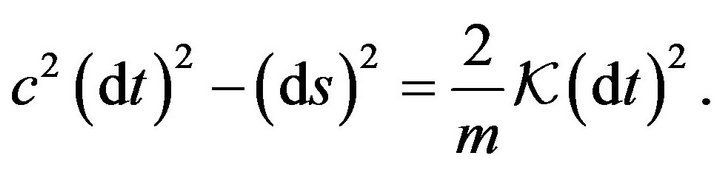 (3)
(3)
This means that if , where
, where 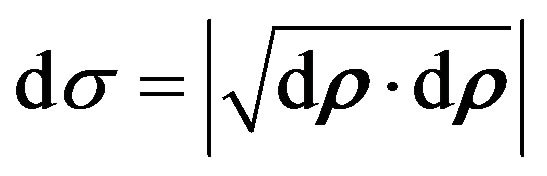 is a line element of the metric affine space of the space-time continuum, then the four-dimensional integral space has the Minkowski metric, [1,4]. So, in this case the Minkowski metric (3) represents the kinetic energy
is a line element of the metric affine space of the space-time continuum, then the four-dimensional integral space has the Minkowski metric, [1,4]. So, in this case the Minkowski metric (3) represents the kinetic energy 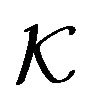 of
of 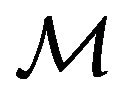 in the integral space. Hence, the Minkowski metric
in the integral space. Hence, the Minkowski metric  is the kinetic metric of the integral space, [6].
is the kinetic metric of the integral space, [6].
If the Pfaff form 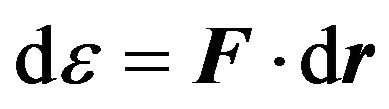 is absolute differential, that means that there exists a scalar valued function
is absolute differential, that means that there exists a scalar valued function 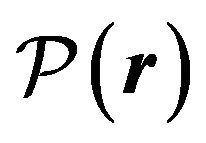 such that
such that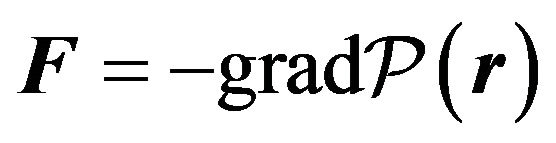 , then
, then 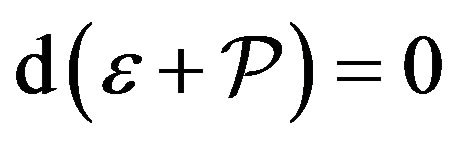 and
and
 (4)
(4)
where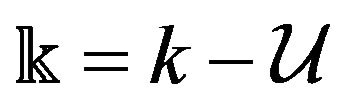 , and
, and  is the total mechanical energy of
is the total mechanical energy of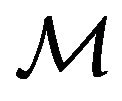 .
.
Now, we can start with the action 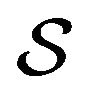 in the Lagrange sense along a motion path of
in the Lagrange sense along a motion path of 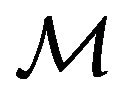 in the integral space [4, 6],
in the integral space [4, 6],
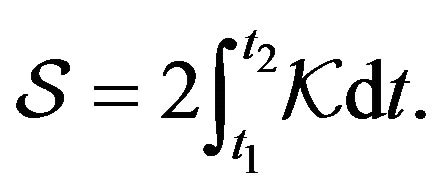 (5)
(5)
Since 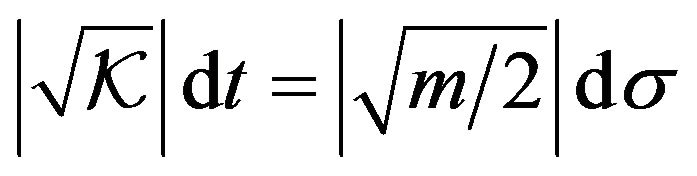 it follows from (4) and (5) that
it follows from (4) and (5) that
 (6)
(6)
Let us introduce an action line element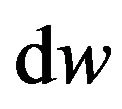 , thoroughly explained in [6], in such a way that
, thoroughly explained in [6], in such a way that
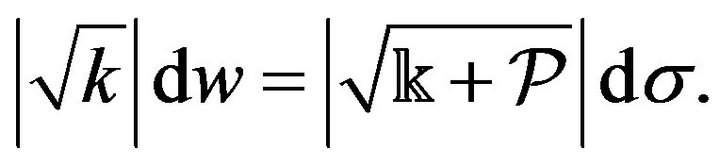 (7)
(7)
Accordingly, the action metric is as follows
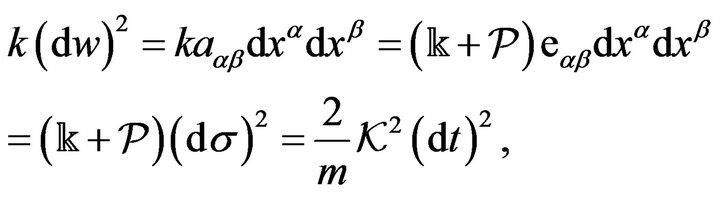 (8)
(8)
where
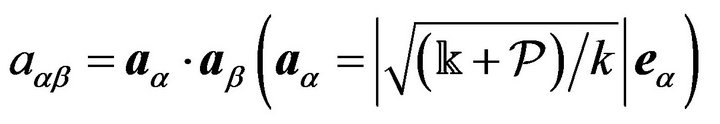
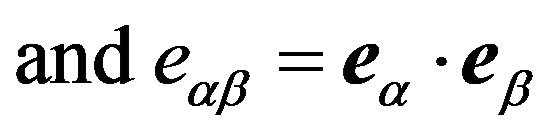 are the metric tensors of
are the metric tensors of 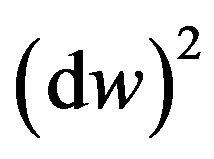 and
and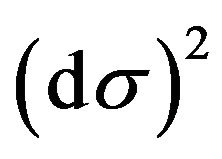 , respectively.
, respectively.
3.1. Newton’s Equations of Motion
By the well-known Maupertius-Lagrange’s principle [4], the path motion of  is just the path along which the action is stationary, more precisely along which the following two mutually equivalent conditions
is just the path along which the action is stationary, more precisely along which the following two mutually equivalent conditions
 (9)
(9)
where ![]() is the variational operator, are satisfied. By (7), the previous conditions are reduced to
is the variational operator, are satisfied. By (7), the previous conditions are reduced to
 (10)
(10)
The second condition in (9) leads to the Euler Lagrange equations
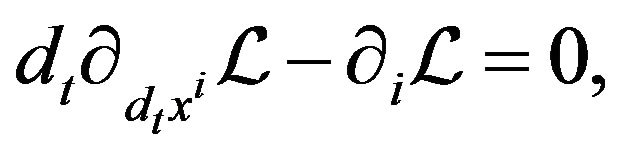 (11)
(11)
where 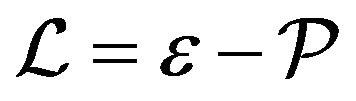 and
and
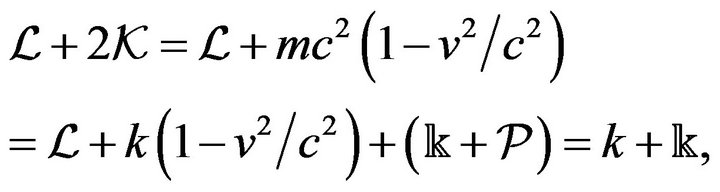
which yield Newton’s equations of motion
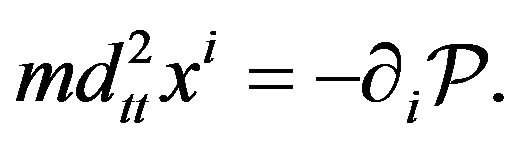 (12)
(12)
3.2. The Relativistic Hamilton-Jacobi Equation for a Free Particle
Analyze (5) again, but now let  be a function of
be a function of that means that
that means that . As
. As
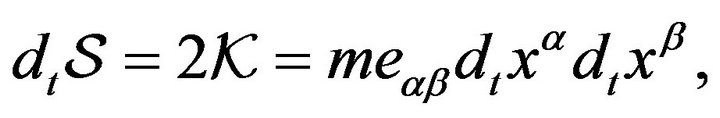 (13)
(13)
we introduce the functional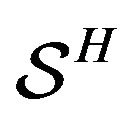 , nominally equal to
, nominally equal to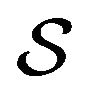 , such that
, such that
 (14)
(14)
as well as the functional 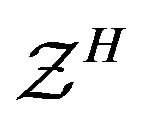 satisfying the condition
satisfying the condition
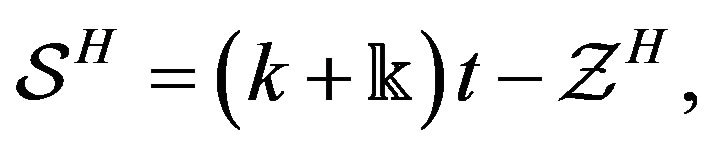 (15)
(15)
which together with (15) yields
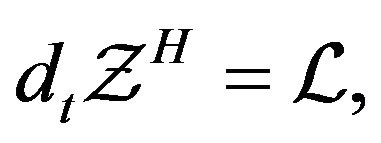 (16)
(16)
since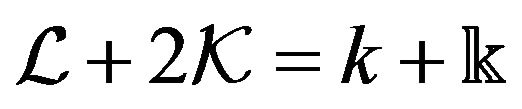 . Hence,
. Hence, 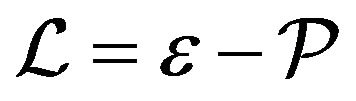 is Lagrangian of
is Lagrangian of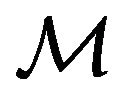 . Further, since
. Further, since 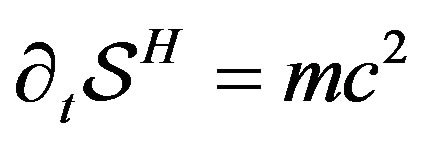 for
for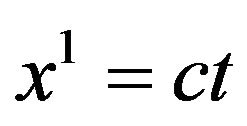 , see (14), it follows from (15) that
, see (14), it follows from (15) that 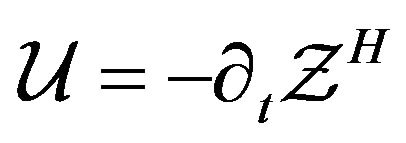 and
and
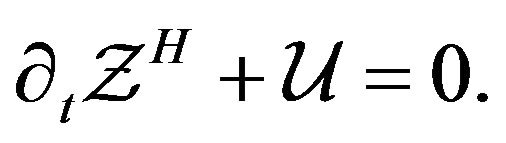 (17)
(17)
The previous equation is the Hamilton-Jacobi one, so that 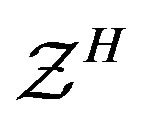 is the principal Hamilton’s functional of
is the principal Hamilton’s functional of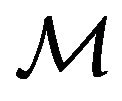 . Clearly, the Hamiltonian
. Clearly, the Hamiltonian  of
of 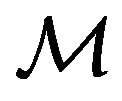 is equal to
is equal to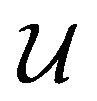 , more precisely to the integral of motion, considering the fact that the kinetic energy
, more precisely to the integral of motion, considering the fact that the kinetic energy ![]() of
of 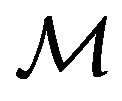 is a homogenous square function of
is a homogenous square function of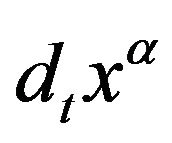 . Now, by (14) and (15), we have
. Now, by (14) and (15), we have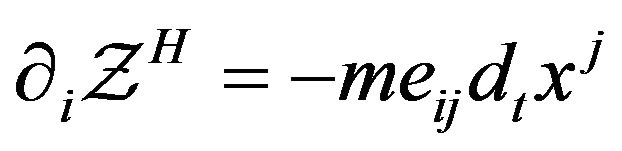 , so that
, so that
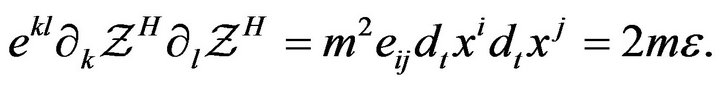 (18)
(18)
This together with (17) leads to the second form of the Hamilton-Jacobi equation
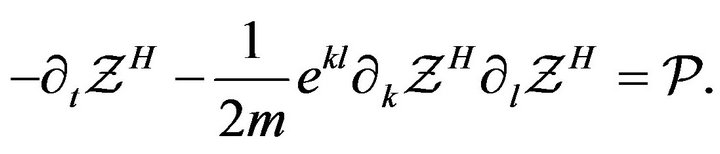 (19)
(19)
In addition,
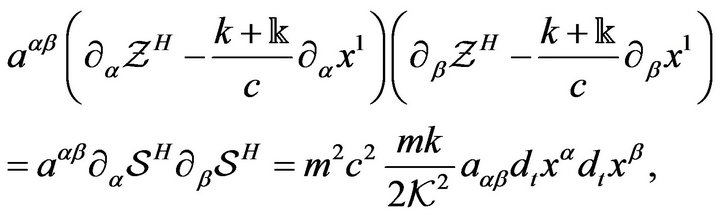 (20)
(20)
which together with (8) yields
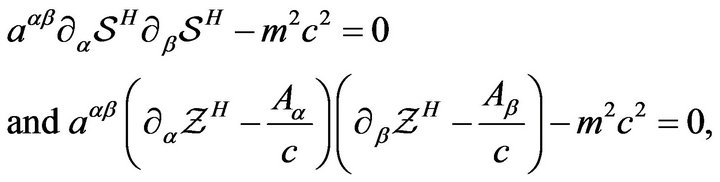 (21)
(21)
where . These two equations are obviously analogous to the relativistic Hamilton-Jacobi equation for a free particle, see [7,8].
. These two equations are obviously analogous to the relativistic Hamilton-Jacobi equation for a free particle, see [7,8].
4. The Binet Differential Equation
As is well-known from the tensorial analysis, see [6], all curves of the integral space, for which the condition (10) is satisfied, are geodesics, and the absolute Bianchi (covariant) derivative ![]() of the unit tangent vector
of the unit tangent vector 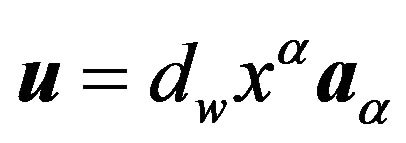 along geodesics is equal to zero (the vector projection of
along geodesics is equal to zero (the vector projection of ![]() onto the tangent hyper-plane of the integral space is equal to zero). Thus, the geodesic equations are as follows
onto the tangent hyper-plane of the integral space is equal to zero). Thus, the geodesic equations are as follows
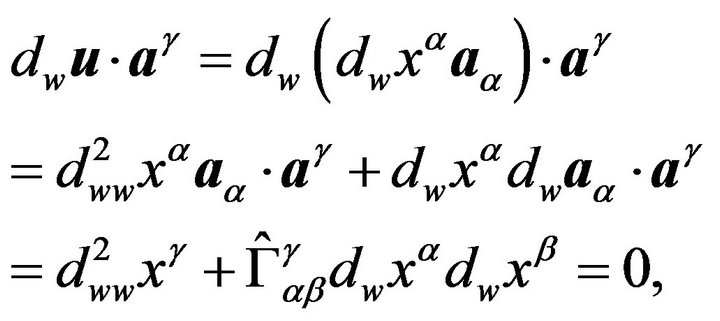 (22)
(22)
where 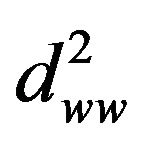 denotes
denotes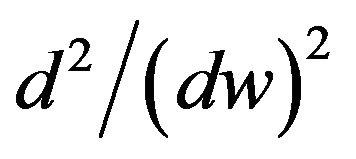 , and
, and
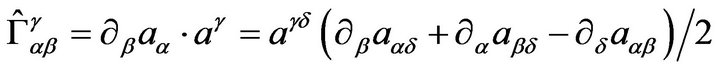 are the second kind Christoffel symbols with respect to the action metric space
are the second kind Christoffel symbols with respect to the action metric space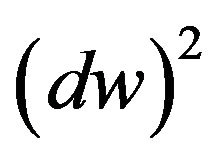 . Let
. Let . Since
. Since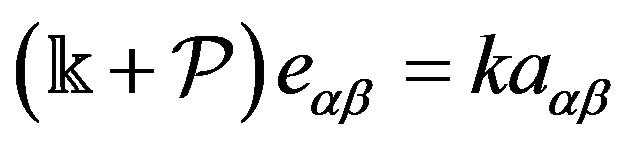 , see (8), it follows that
, see (8), it follows that
 (23)
(23)
where  are the second kind Christoffel symbols with respect to the Euclidean metric space
are the second kind Christoffel symbols with respect to the Euclidean metric space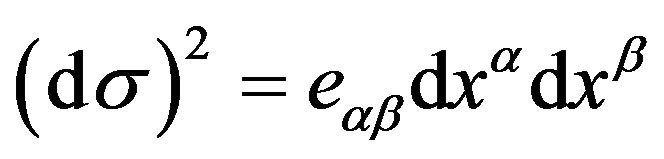 . A new form of the geodesic equations (22), for a constrained material point
. A new form of the geodesic equations (22), for a constrained material point , is as follows
, is as follows
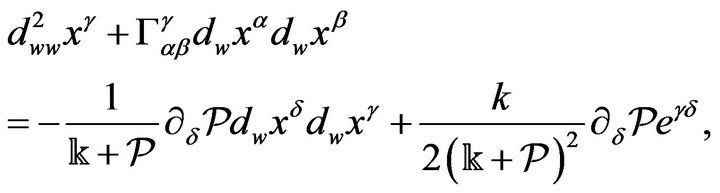 (24)
(24)
which yields
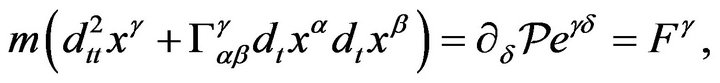 (25)
(25)
since
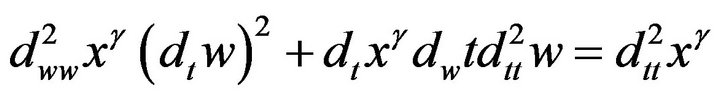 ,
,
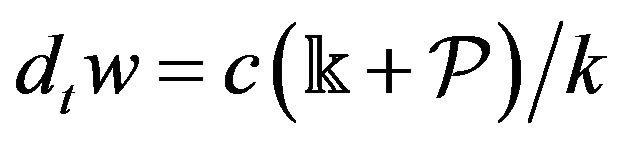 and
and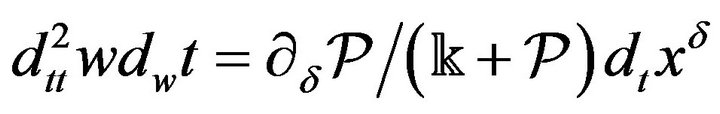 .
.
So, (25) represents the Euler-Lagrange differential equations of the extremal curve in the explicit form, and at the same time Newton’s second law of motion under the action of a potential force 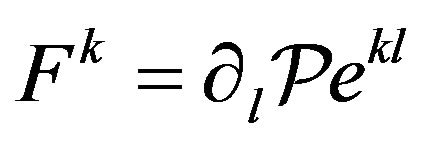 in the contravariant form:
in the contravariant form:
 (26)
(26)
Accordingly, one may conclude that the dynamic (Newton’s) Equations (26) of motion are formally derived from the geometric Equations (22).
In the case of the free motion of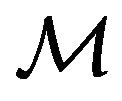 , when
, when , both the kinetic and action metric form of the integral space are pseudo-euclidean, while integral curves are straight-lines (see Appendix), as it was thoroughly explained in the monograph by [6]. On the other hand, the well-known Binet differential equation for central force motion of
, both the kinetic and action metric form of the integral space are pseudo-euclidean, while integral curves are straight-lines (see Appendix), as it was thoroughly explained in the monograph by [6]. On the other hand, the well-known Binet differential equation for central force motion of 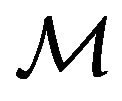
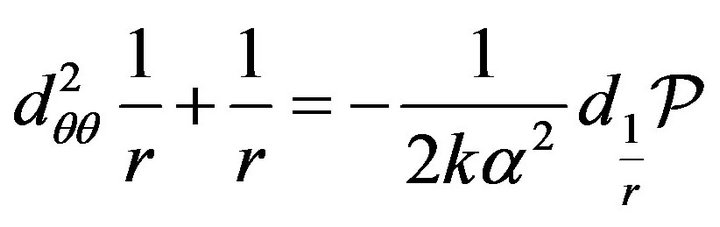 (27)
(27)
is obtained by differentiating (58) (see Appendix).
5. Modified Newton’s Gravity Concept
For the conservative Newton’s gravity force 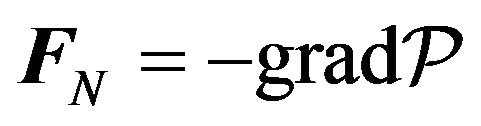 the expression
the expression 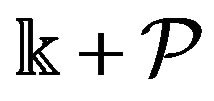 is as follows
is as follows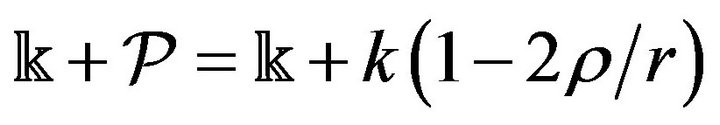 , where
, where 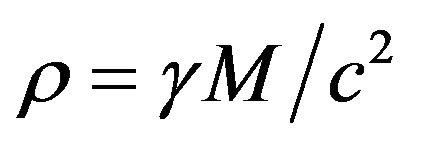 is the gravitational radius, so that (27) is reduced to
is the gravitational radius, so that (27) is reduced to
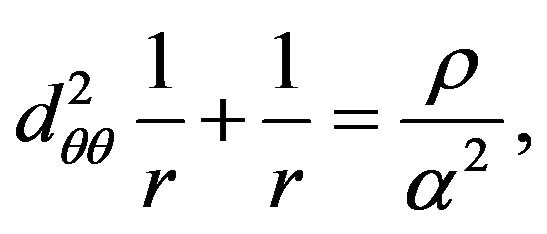 (28)
(28)
where 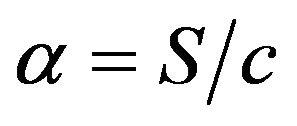 and
and .
.
Since, in the limit as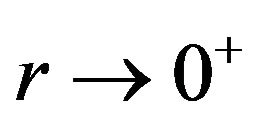 , Newton’s gravitational potential
, Newton’s gravitational potential 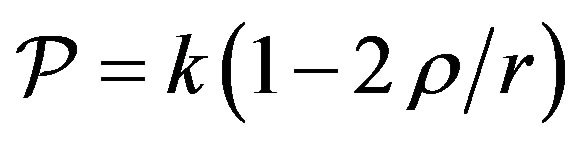 tends to infinity, it is logical to assume that
tends to infinity, it is logical to assume that  is the first-order MacLaurin series approximation of the exponential function
is the first-order MacLaurin series approximation of the exponential function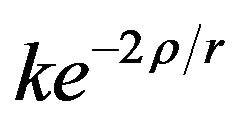 , so that
, so that 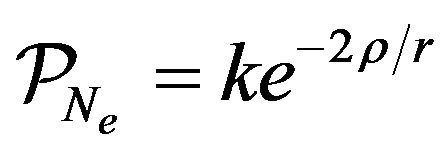 and
and
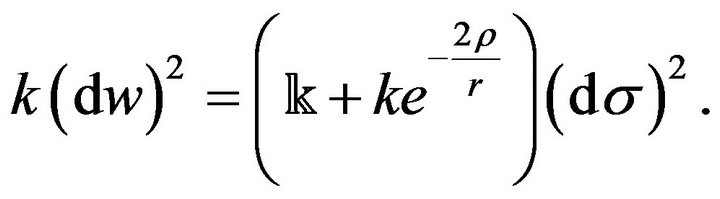 (29)
(29)
Accordingly, the modified Binet differential equation for the modified central Newton’s gravity force
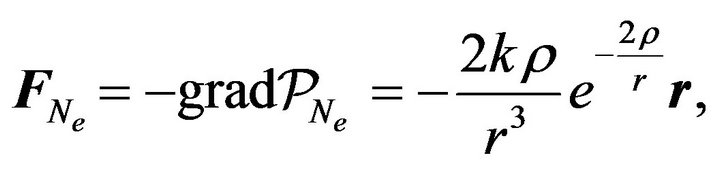 (30)
(30)
is as follows
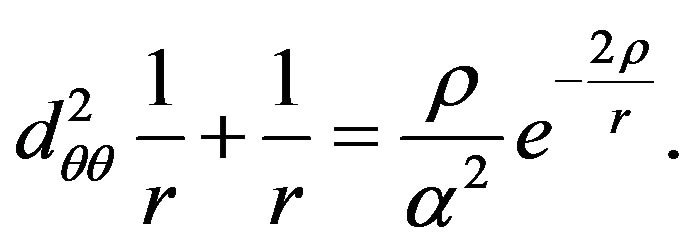 (31)
(31)
5.1. A motion Under the Action of 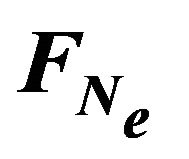
Start with Newton’s second law of motion
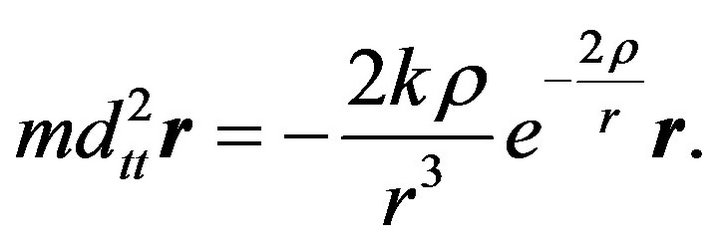 (32)
(32)
Multiply (32) on the right by the sector velocity vector 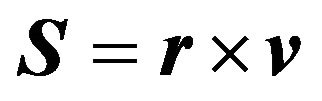 as follows
as follows
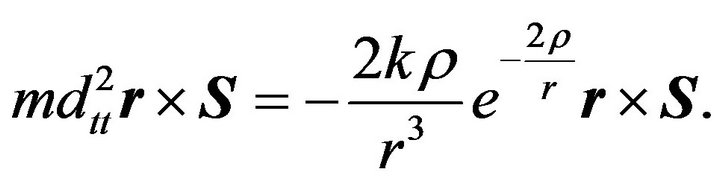 (33)
(33)
Since 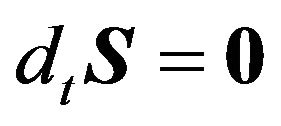 it follows from (33) that
it follows from (33) that
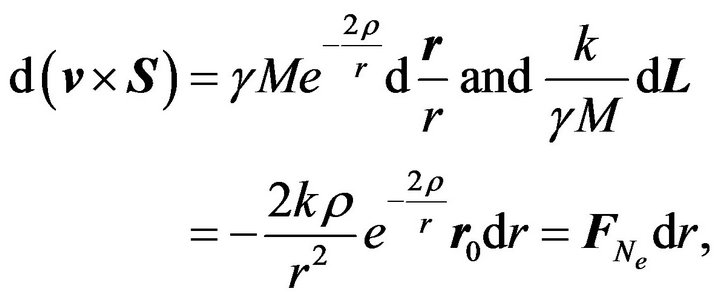 (34)
(34)
where the vector 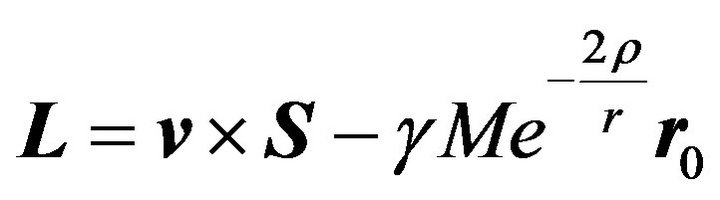 satisfying the relation
satisfying the relation 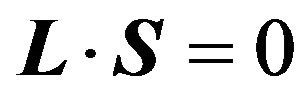 is no longer an element of Milankovic’s constant vector elements, more precisely is no longer Laplace’s integration vector constant, see [9]. If we now multiply
is no longer an element of Milankovic’s constant vector elements, more precisely is no longer Laplace’s integration vector constant, see [9]. If we now multiply ![]() by
by , we get
, we get
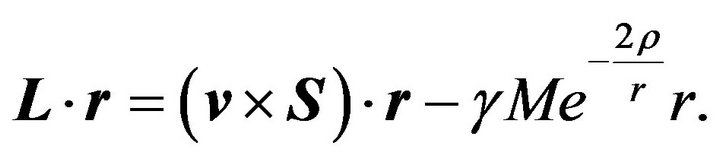 (35)
(35)
Since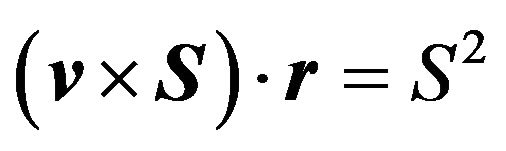 , it follows from (35) that
, it follows from (35) that
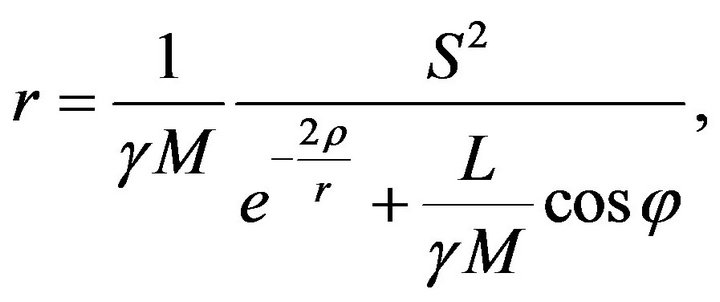 (36)
(36)
where ![]() is an angle between
is an angle between 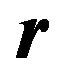 and
and![]() . This equation describes the motion of
. This equation describes the motion of 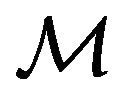 under the action of the modified Newton’s gravity force
under the action of the modified Newton’s gravity force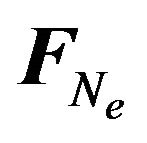 . Conditionally speaking, there is no formal difference between (36) and its analog in the ordinary Newton’s gravity theory. The key difference lies in the fact that
. Conditionally speaking, there is no formal difference between (36) and its analog in the ordinary Newton’s gravity theory. The key difference lies in the fact that ![]() is no longer constant vector.
is no longer constant vector.
For 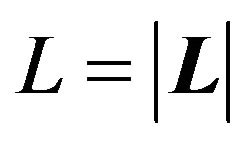 let
let 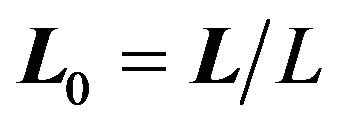 and
and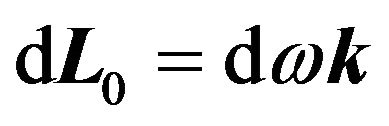 , where
, where ![]() is the unit vector orthogonal to
is the unit vector orthogonal to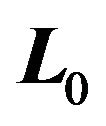 . Then, from (34) we get
. Then, from (34) we get
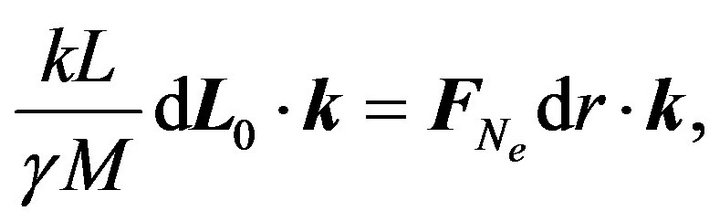 (37)
(37)
which together with (36) yields
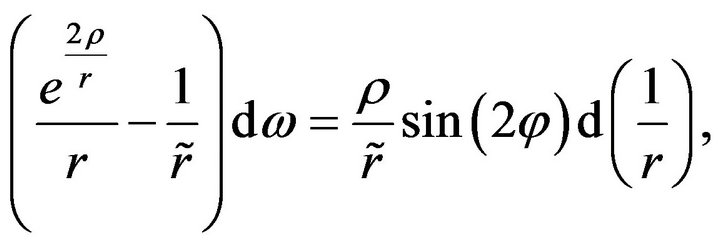 (38)
(38)
where 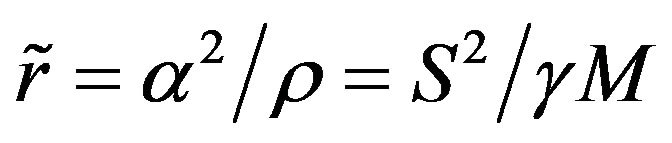 and
and
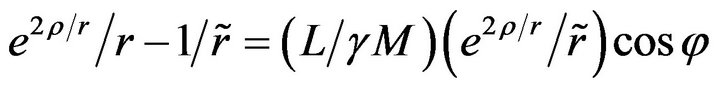 .
.
In addition, the dot product 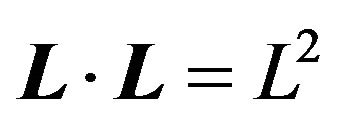 leads to
leads to
 (39)
(39)
Thus,
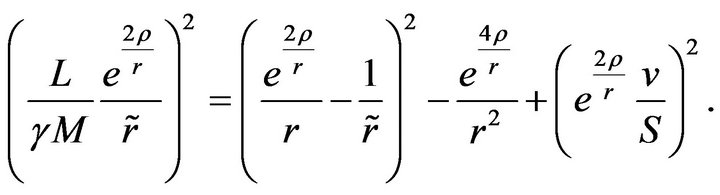 (40)
(40)
If ![]() is the angle between
is the angle between  and
and![]() , it follows from (36) and (40) that
, it follows from (36) and (40) that
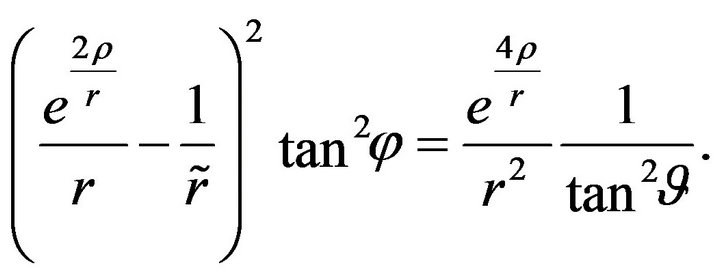 (41)
(41)
Hence,
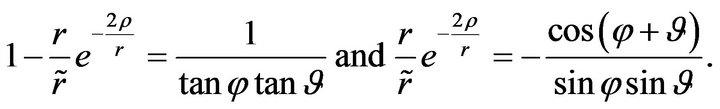 (42)
(42)
Note that , whenever
, whenever . If we now multiply (38) by
. If we now multiply (38) by 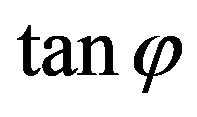 we get
we get
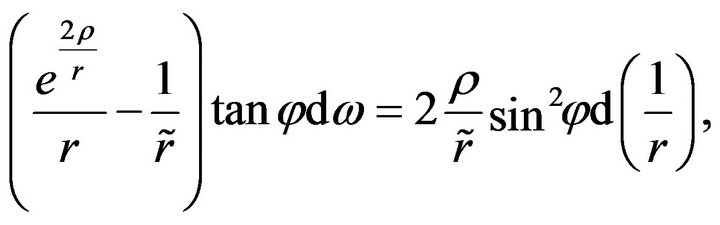 (43)
(43)
which together with (41) and (42) yields
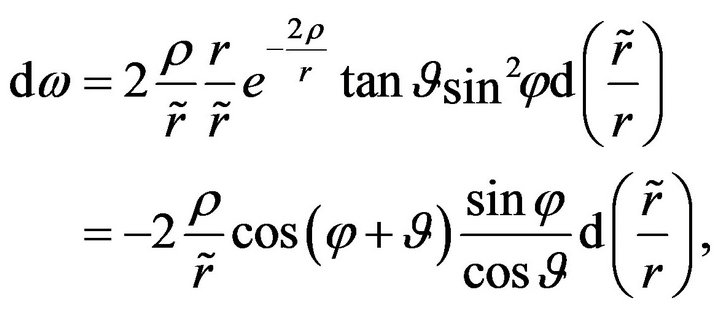 (44)
(44)
whenever . If
. If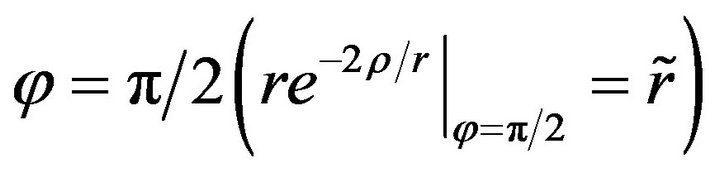 , then
, then
 (45)
(45)
Since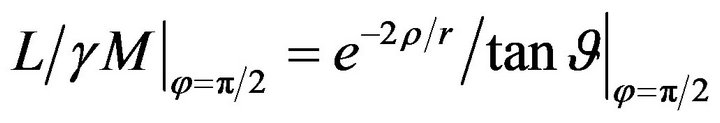 , see (38), it follows from (36) that
, see (38), it follows from (36) that
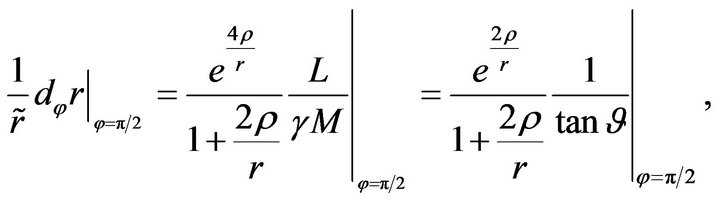 (46)
(46)
which together with (45) finally yields
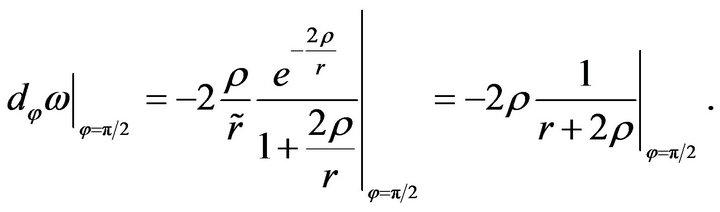 (47)
(47)
This result we can also get explicitly from (46). Namely, if  is the polar angle, then
is the polar angle, then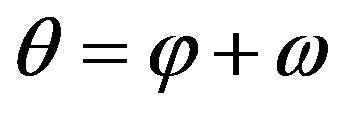 . Therefore, it follows from (46) that
. Therefore, it follows from (46) that
 (48)
(48)
Since 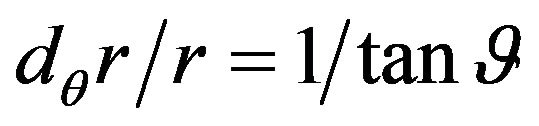 we have
we have
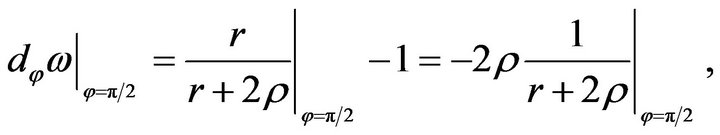 (49)
(49)
that is just the same as (47). Hence,
 (50)
(50)
So, as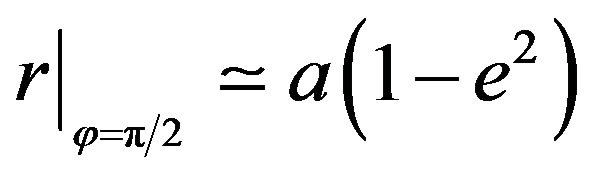 , where
, where ![]() and
and ![]() are the semimajor axis and the eccentricity of the orbit, the following angle value
are the semimajor axis and the eccentricity of the orbit, the following angle value
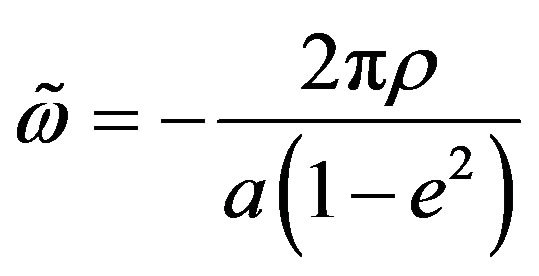 (51)
(51)
is a very good approximation for the perihelion regression ![]() per one revolution
per one revolution 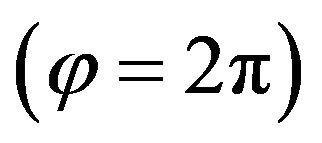 of the Planets.
of the Planets.
5.2. The Modified Perturbing Force
If, in addition to the modified Newton’s gravity force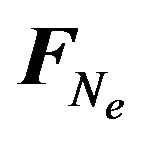 , we include the modified perturbing force [10]
, we include the modified perturbing force [10]
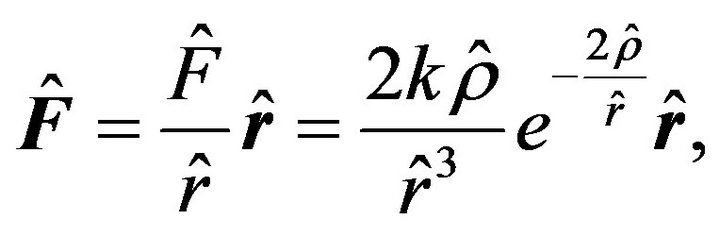
where  and
and 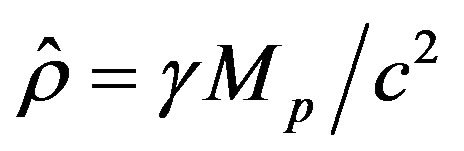 are the radial vector between the Planet and the perturbing planet (whose orbit is assumed to be circular and coplanar with Mercury’s orbit) and the gravitational radius for the perturbing planet, respectively, then
are the radial vector between the Planet and the perturbing planet (whose orbit is assumed to be circular and coplanar with Mercury’s orbit) and the gravitational radius for the perturbing planet, respectively, then
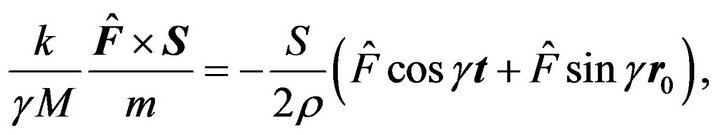
where 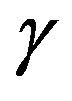 is the angle between
is the angle between  and
and , and
, and  is the unit vector perpendicular to
is the unit vector perpendicular to![]() . Thus, the second equation of (35) becomes
. Thus, the second equation of (35) becomes

where 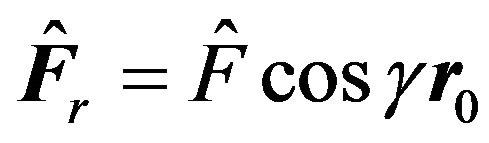 and
and
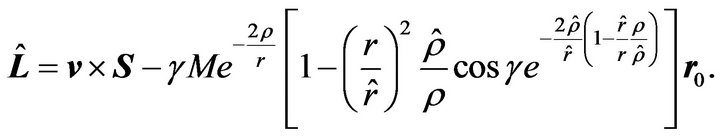
This vector is the modified Laplace’s integration vector (or more precisely, the modified Laplace-RungeLenz vector). Their original versions come from the ordinary Newton’s gravity theory. If we denote
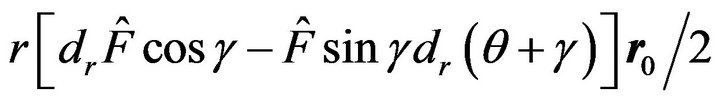
by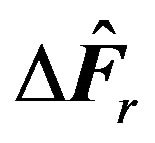 , then we have
, then we have

6. Conclusion
The mathematical model of a material point motion in the three-dimensional spatial subspace of the four-dimensional space-time continuum and in the field of the action of a conservative active force  is analogous to Newton’s mathematical model of the classical mechanics. In addition, the metric
is analogous to Newton’s mathematical model of the classical mechanics. In addition, the metric 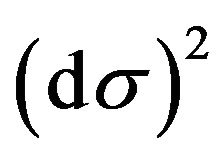 of the integral space, which represents the kinetic energy of a material point from the viewpoint of that space, is the Minkowski metric from Einstein’s relativity theory. Accordingly, it can be said that in the paper a new connection has been established, in contrast to an approximative one, between the classical Newton’s mathematical model and the relativistic Einstein’s mathematical model.
of the integral space, which represents the kinetic energy of a material point from the viewpoint of that space, is the Minkowski metric from Einstein’s relativity theory. Accordingly, it can be said that in the paper a new connection has been established, in contrast to an approximative one, between the classical Newton’s mathematical model and the relativistic Einstein’s mathematical model.
On the other hand the approximately modified Newton’s gravity concept is not, from any point of view, in collision with old Newton’s one. At the same time it solves the acutely vexed questions within old Newton’s gravity concept (the singularity and perihelion problems). Furthermore, analyzing the analytical expression for the modified Newton’s gravity force , we can separate the four indicative domains of its field of the action (see Figure 1). The first one is a domain of the weak action on finitely small distances. The second one is a domain
, we can separate the four indicative domains of its field of the action (see Figure 1). The first one is a domain of the weak action on finitely small distances. The second one is a domain
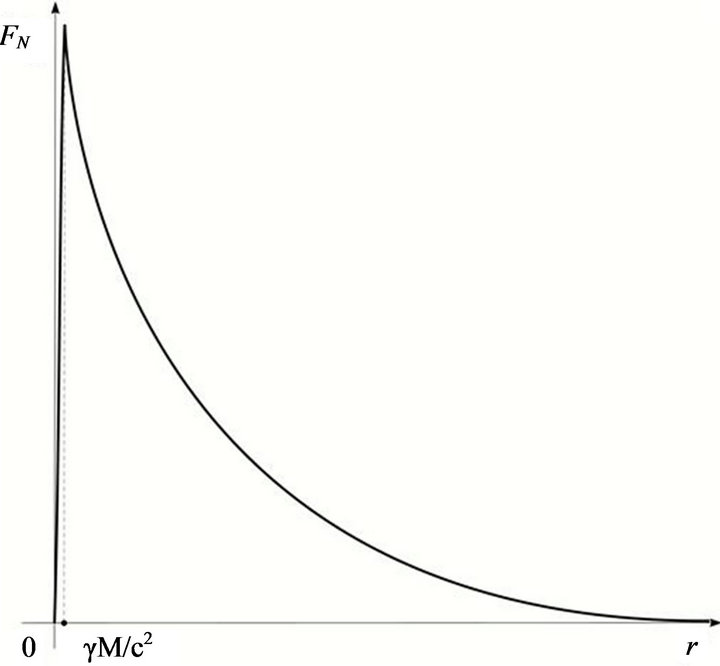
Figure 1. Modified Newton’s gravity force.
of the strong action in a neighborhood of the gravitational radius
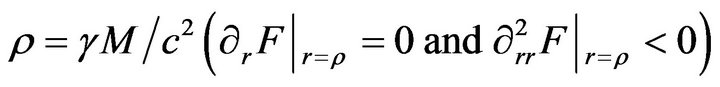 . The third one is a domain of the action on finitely large distances relative to the gravitational radius
. The third one is a domain of the action on finitely large distances relative to the gravitational radius  and with the relatively small velocities relative to the light velocity, and the fourth on finitely large distances relative to the gravitational radius
and with the relatively small velocities relative to the light velocity, and the fourth on finitely large distances relative to the gravitational radius  and with velocities that are comparable to the light velocity. Previously separated domains of the field of the action of the modified Newton’s gravity force
and with velocities that are comparable to the light velocity. Previously separated domains of the field of the action of the modified Newton’s gravity force 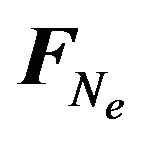 it would be desirable to compare to the fields of the action of the four so far non-unified fundamental forces (weak and strong nuclear interactions, gravity and Lorenz’s electromagnetism). Clearly, all of these facts aforementioned could be subject of further analyses. Note at the end that a correction to Newton’s gravity law in the form of the functional dependence
it would be desirable to compare to the fields of the action of the four so far non-unified fundamental forces (weak and strong nuclear interactions, gravity and Lorenz’s electromagnetism). Clearly, all of these facts aforementioned could be subject of further analyses. Note at the end that a correction to Newton’s gravity law in the form of the functional dependence 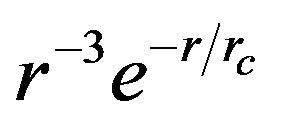
 irresistibly reminding of the modified Newton’s gravity force, and obviously wrongly called the fifth force, has been revealed by a reexamination of the old attraction data and careful new force measurements presented in [11].
irresistibly reminding of the modified Newton’s gravity force, and obviously wrongly called the fifth force, has been revealed by a reexamination of the old attraction data and careful new force measurements presented in [11].
REFERENCES
- I. S. Lukačević, “Elements of the Relativity Theory,” Scientific Book, Belgrade, 1980.
- G. E. Tauber, “The General Einstein’s Relativity Theory,” Globe, Zagreb, 1984.
- Lj. T. Grujić, “Relativity and Physical Principle. Generalizations and Applications,” Proceedings of VI International Conference: Physical Interpretations of Relativity Theory, London, 11-14 September 1998, pp. 134-155.
- V. Pauli, “The Relativity Theory,” Science, Moscow, 1983.
- L. D. Landau and E. M. Lifšic, “The Fields Theory,” Science, Moscow, 1988.
- T. P. Anđelić, “Tensorial Calculus,” Scientific Book, Belgrade, 1980.
- V. M. Villalba and W. Greiner, “Creation of Dirac Particles in the Presence of a Constant Electric Field in an Anisotropic Bianchi I Universe,” Modern Physics Letters A, Vol. 17, No. 28, 2002, pp. 1883-1891. doi:10.1142/S0217732302008289
- S. Fedotov, “Front Dynamics for an Anisotropic Reaction-Diffusion Equation,” Journal of Physics A: Mathematical and General, Vol. 33, No. 40, 2000, pp. 7033- 7042.
- D. Mihailović, “On Some Relations between Vector Elements,” Publication of School of Electrical Engineering of Belgrade University, Series: Mathematics and Physics, Vol. 302-319, 1970, pp. 73-76.
- M. G. Stewart, “Precession of the Perihelion of Mercury’s Orbit,” American Journal of Physics, Vol. 73, No. 8, 2005, pp. 730-734. doi:10.1119/1.1949625
- P. G. Bizetti, A. M. Bizetti-Sona, T. Fazzini and N. Tacceti, “Search for a Composition-Dependent Fifth Force,” Physical Review Letters, Vol. 62, No. 25, 1989, pp. 2901- 2904. doi:10.1103/PhysRevLett.62.2901
Appendix: The Freee Motion of ![]() in the Integral Space
in the Integral Space
Let us start with the Euler-Lagrange equations
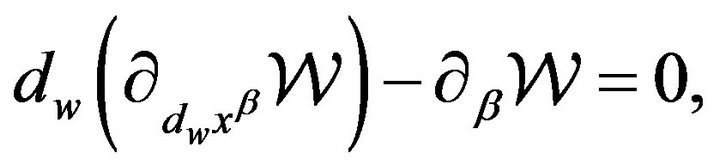 (52)
(52)
where
 (53)
(53)
as the condition for the action (12) to be stationary. The geodesic Equations (13) are explicitly obtained from it in a known way. If spatial co-ordinates are spherical ones , then the components of
, then the components of 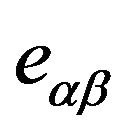 depend only on
depend only on  and
and![]() , so that it follows from (52) that
, so that it follows from (52) that
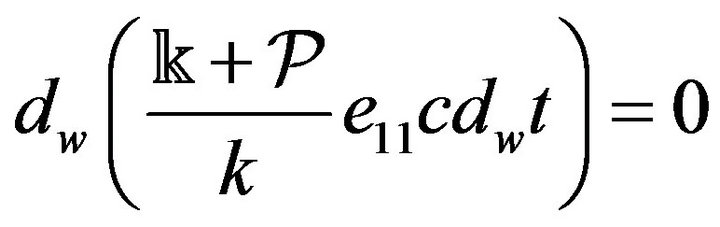 (54)
(54)
and
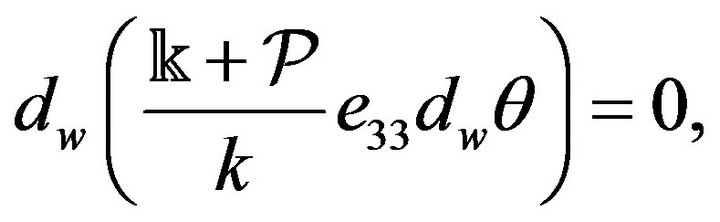 (55)
(55)
that leads to
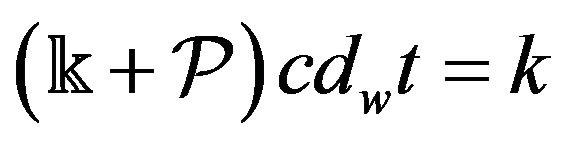 (56)
(56)
and
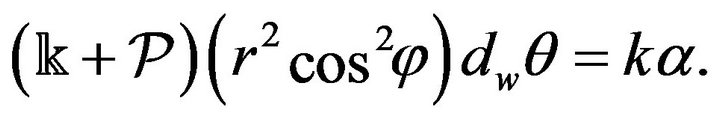 (57)
(57)
Let the polar extension 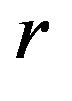 and the polar angle
and the polar angle  be intensities of
be intensities of  and an angle between the position vector
and an angle between the position vector 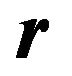 and the polar axis
and the polar axis ![]() passing through the origin and the perihelial point, respectively. Then, since
passing through the origin and the perihelial point, respectively. Then, since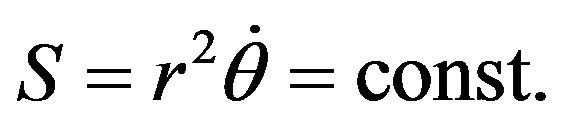 , where
, where 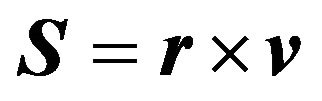 is the so-called sector velocity vector, it follows from the condition (57) that the motion is the plane one
is the so-called sector velocity vector, it follows from the condition (57) that the motion is the plane one 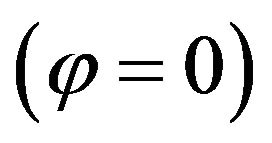 and
and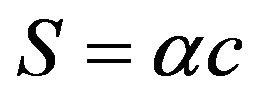 . As
. As 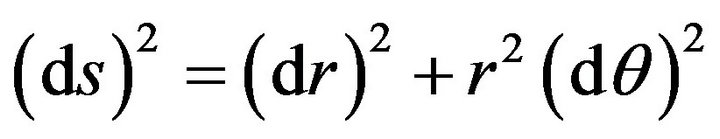 then we obtain finally from (5), (10) and (57) that
then we obtain finally from (5), (10) and (57) that
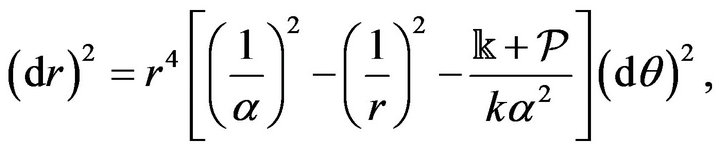 (58)
(58)
that just leads to the Binet differential equation for free motion in plane polar co-ordinates
 (59)
(59)
The solution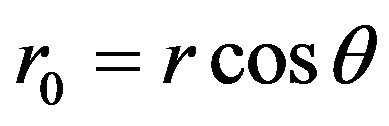 , where
, where![]() is the perihelial distance, to this differential equation, defines a straightline in plane polar co-ordinates.
is the perihelial distance, to this differential equation, defines a straightline in plane polar co-ordinates.

