Applied Mathematics
Vol.3 No.8(2012), Article ID:21487,4 pages DOI:10.4236/am.2012.38135
A Novel Non-Equidistant Grey GRM(1,1) Model Based on Reciprocal Accumulated Generating
College of Sciences, Hunan Agriculture University, Changsha, China
Email: rbzou@163.com
Received June 6, 2012; revised July 5, 2012; accepted July 13, 2012
Keywords: GRM Model; Non-Equidistant Interval; Accumulated Generating; Grey System
ABSTRACT
Applying the reciprocal accumulated generating and the reconstruction method of GRM(1,1) model’s background value of non-equidistant sequence based on the exponential trait of grey model and the definition of integral for the problem of lower precision as well as lower adaptability in non-equidistant GM(1,1) model, the calculation formulas were deduced and a novel non-equidistant GRM(1,1) model generated by reciprocal accumulated generating was put forward. The grey GRM(1,1) model can be used in non-equidistant interval & equidistant interval time series and has the characteristic of high precision as well as high adaptability. Example validates the practicability and reliability of the proposed model.
1. Introduction
Grey model as an important part in grey system theory has been widely used in many fields since Professor J.L. Deng proposed the grey system [1]. Among the models, GM(1,1) has been greatly concerned and been widely used because of the research characteristics such as the small sample and the poor information, as well as the advantages which is simple and practical [1-6]. Most of the grey system models are based on equidistant sequence, but the original data obtained from the actual work are mostly non-equidistant sequence. So that establishing non-equidistant sequence model has a certain practical and theoretical significance. Sequence spacing was regarded as a multiplier to establish the non-equidistance GM(1,1) model which supposed that there is the linear relationship between data difference and time difference [2], but the result from this model can’t be ensured to be consistent with the reality. Function transformation method was adopted to reduce the standard deviation coefficient to take the original sequence as new data sequence and estimate the model parameters, and then GM(1,1) was set up [3], but there is the complicated calculation. In order to improve the accuracy of the fitting and the predict, a variety of methods constructing the background value were proposed and some nonequidistant GM(1,1) models were established [4-6]. The model improving the background value based on nonhomogeneous GM(1,1) model was established, in which homogeneous exponent function is used for fitting onetime accumulated generating sequence to obtain the higher accuracy [4,5]. But according to the solution form of the whitening differential equations in GM(1,1), the exponent form of one-time accumulated generating sequence is non-homogeneous, and only after accumulating and reducing it is homogeneous. There produce some error by using the homogeneous exponent function to fit. The optimal calculation formula for background value was deduced using non-homogeneous exponent function to fit one-time accumulated generating sequence and equidistant GM(1,1) model was established [6]. But these models are based on common accumulated or inverse accumulated generation in the process of modeling. For non-negative discrete sequence , the one-time accumulated generation sequence
, the one-time accumulated generation sequence 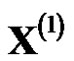 is monotonically increasing. When a curve fits
is monotonically increasing. When a curve fits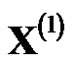 , it is reasonable that the curve is monotonically increasing. It is GM(1, 1) to predict. If
, it is reasonable that the curve is monotonically increasing. It is GM(1, 1) to predict. If 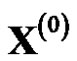 itself is monotonically decreasing,
itself is monotonically decreasing, 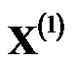 is monotonically increasing and then the model value
is monotonically increasing and then the model value 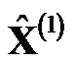 is also increased. When
is also increased. When 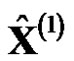 is regressively generated to the predicted value of the original sequence
is regressively generated to the predicted value of the original sequence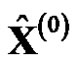 , there will produce an unreasonable calculation errors. For the original sequence with monotonically decreasing trend, accumulated generation in opposite direction was put forward and GOM (1,1) based on accumulated accumulation in opposite direction was established [7]. GRM(1,1) based on reciprocal generation was built after proposing reciprocal generation [8]. GRM(1,1) was improved to establish the improved grey model CGRM(1,1) based on reciprocal generation [9]. The models that based on reciprocal generation and opposite-direction accumulated generation make the generation sequence
, there will produce an unreasonable calculation errors. For the original sequence with monotonically decreasing trend, accumulated generation in opposite direction was put forward and GOM (1,1) based on accumulated accumulation in opposite direction was established [7]. GRM(1,1) based on reciprocal generation was built after proposing reciprocal generation [8]. GRM(1,1) was improved to establish the improved grey model CGRM(1,1) based on reciprocal generation [9]. The models that based on reciprocal generation and opposite-direction accumulated generation make the generation sequence 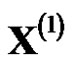 monotone decreasing, and then fitted
monotone decreasing, and then fitted 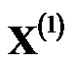 by using the decreasing monotonically curve to obtain the model value
by using the decreasing monotonically curve to obtain the model value 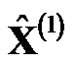 of
of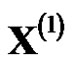 .In this case, the reduction process from
.In this case, the reduction process from  to
to 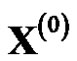 will not produce the unreasonable error and it improves modeling accuracy. But the models in [8,9] are equidistant GRM(1,1). Based on reciprocal accumulated generation combining with the method establishing background value in [4], this paper deduced the model calculation formulas, and established a non-equidistant grey GRM(1,1) model based on reciprocal accumulated generation. This model with high precision has better practical and theoretical significance. Example validates the practicability and reliability of the proposed model.
will not produce the unreasonable error and it improves modeling accuracy. But the models in [8,9] are equidistant GRM(1,1). Based on reciprocal accumulated generation combining with the method establishing background value in [4], this paper deduced the model calculation formulas, and established a non-equidistant grey GRM(1,1) model based on reciprocal accumulated generation. This model with high precision has better practical and theoretical significance. Example validates the practicability and reliability of the proposed model.
2. Non-Equidistant Grey GRM(1,1) Model
Definition 1. Supposed the sequence
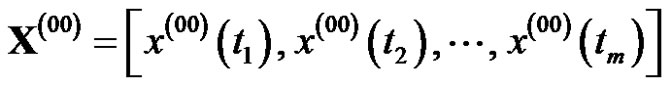 If
If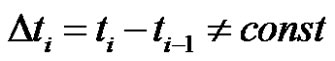 , where
, where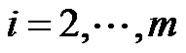 , then
, then  is called as non-equidistant sequence. Supposed
is called as non-equidistant sequence. Supposed
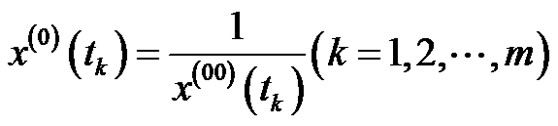 then
then
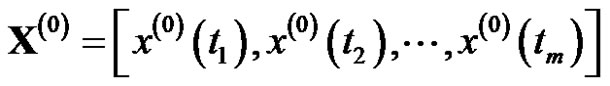
is named for reciprocal sequence of .
.
Definition 2. Supposed the sequence
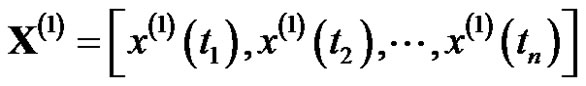 where
where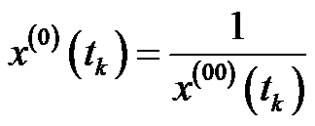 ,
,  , if
, if
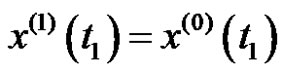
and
 where
where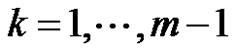 , then
, then 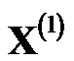 is called as one-time reciprocal accumulated generation of non-equidistant sequence
is called as one-time reciprocal accumulated generation of non-equidistant sequence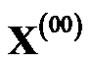 , and it is denoted by 1-RAG0.
, and it is denoted by 1-RAG0.
Supposed the original data sequence
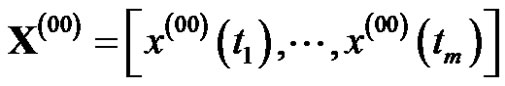 where
where
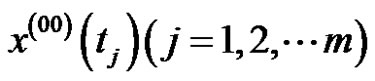
is the observation value at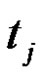 , m is the data number, and the sequence
, m is the data number, and the sequence 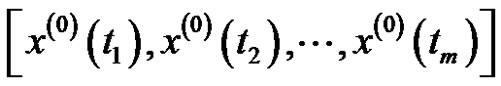 is nonequidistant, that is, the spacing
is nonequidistant, that is, the spacing 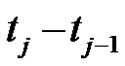 is not constant.
is not constant.
In order to establish the model, firstly the original data is reciprocal accumulated one time to generate a new sequence as:
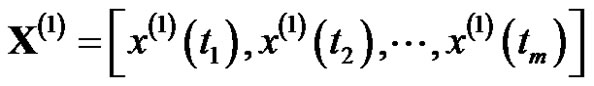 (1)
(1)
where,  meets the conditions in the definition 2, that is,
meets the conditions in the definition 2, that is,
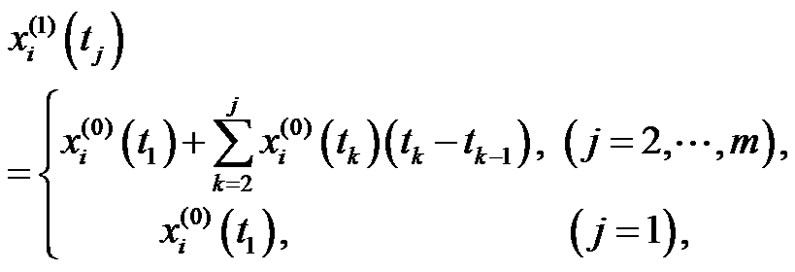 (2)
(2)
Accounting to one-time reciprocal accumulated generation, a non-equidistant GRM(1,1) model is established as a first-order grey differential equation
 where
where 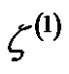 is the background value. Its whitening differential equation is as
is the background value. Its whitening differential equation is as
 .
.
The whitening differential equation is integrated in the interval  as
as
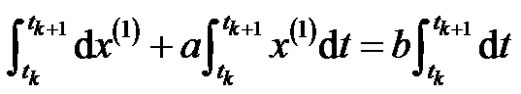 . (3)
. (3)
Supposed
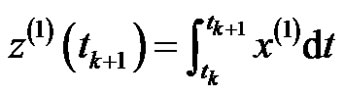
is the background value of  in
in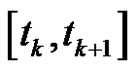 , Equation (3) is converted as
, Equation (3) is converted as
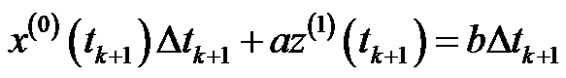 . (4)
. (4)
As the result forms of the whitening differential equation is exponential, 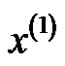 can be fitted by the equation as
can be fitted by the equation as . Supposed that
. Supposed that 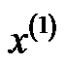 runs through
runs through
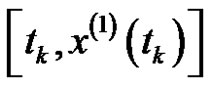 and
and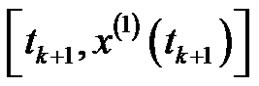 , it can be obtained as:
, it can be obtained as:
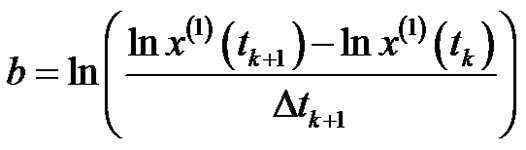 ,
,
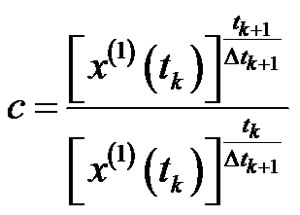 .
.
So the background value can be structured as
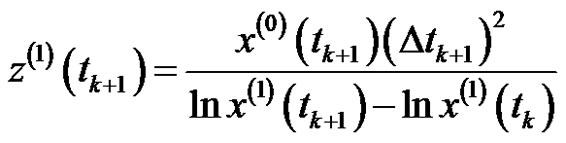 . (5)
. (5)
The matrix of Equation (4) is expressed as
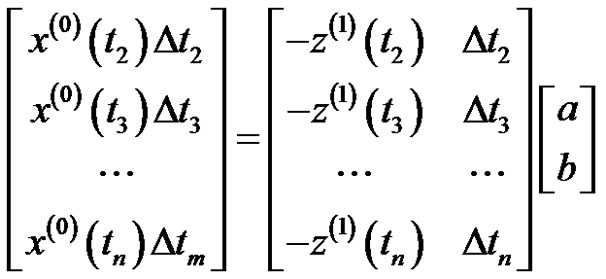 .
.
Assumed
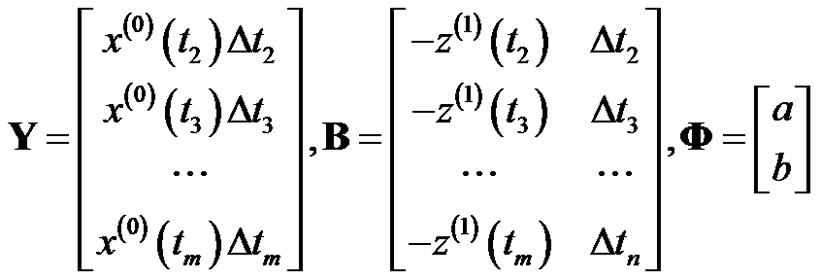 where,
where,  is parameter vector to be identified,
is parameter vector to be identified, ![]() and
and 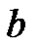 are the constant to be identified. The most leastsquares estimation of
are the constant to be identified. The most leastsquares estimation of  is
is .
.
The discrete solution in the whitening differential Equation 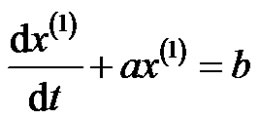 is
is
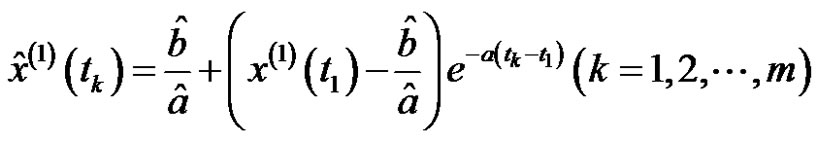 . (6)
. (6)
After restoring the reciprocal fitting value of the original data is
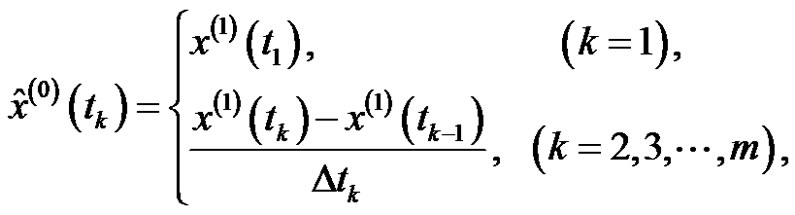 (7)
(7)
Accounting to Definition 1, the model value of the original sequence is .
.
The absolute error of the fitting data is
 . (8)
. (8)
The relative error of the fitting data (%) is
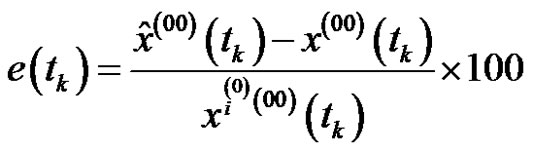 . (9)
. (9)
The mean of the relative error of the fitting data column:
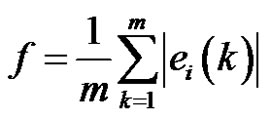 . (10)
. (10)
After obtaining some data such as the simulation value, the predicted value and the error in non-equidistant GRM(1,1), the model can be tested [1]. The calculating program NGRM_I1.0 was compiled with Matlab [10].
3. Example
P. G. Foleiss researched that there is the influence of the temperature on fatigue strength under the long life symmetry cycle of many materials. Table 1 shows the experimental data of the change relation of Ti alloy fatigue strength along with temperature, which is a sequence of non-equidistant spacing. The data in [2,3] were modeled by using the method proposed in this paper and we obtained the following result:
![]() = –0.00097435,
= –0.00097435,  = 0.001774,
= 0.001774,
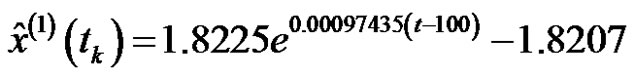 .
.
The fitting value of the original data is
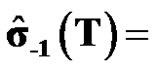 [560,554.9509,536.3301,515.8293498.5487,484.1868,467.9404,452.2641437.0888].
[560,554.9509,536.3301,515.8293498.5487,484.1868,467.9404,452.2641437.0888].
The absolute error of the fitting data is
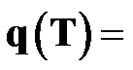 [0, 2.5891, –0.23009, 0.27073, 7.05131.9132, –0.54039, 1.5359, –0.68884].
[0, 2.5891, –0.23009, 0.27073, 7.05131.9132, –0.54039, 1.5359, –0.68884].
The relative error of the fitting data(%)is
 [0.46437, –0.042919, 0.052457, 1.39460.39358, –0.11562, 0.33844, –0.1578].
[0.46437, –0.042919, 0.052457, 1.39460.39358, –0.11562, 0.33844, –0.1578].
The mean of the relative error of the fitting data column is 0.32887%.
The mean relative error in the non-homogeneous model based on traditional accumulated generating in [4] is 0.33666%.
After the original data were pre-processed by using
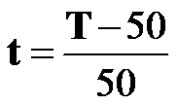 and
and 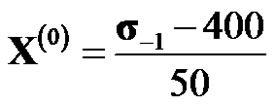 in [2], the maximum relative error is 4.86% and the mean relative error is 3.19%. The model was established by using the function transformation method in [3] and the mean relative error is 0.6587%. Homogeneous exponent function fitting onetime accumulated generating sequence was used in [5] and it is 0.9765%. Thus, the examples validate the adaptability and the scientific of the proposed model.
in [2], the maximum relative error is 4.86% and the mean relative error is 3.19%. The model was established by using the function transformation method in [3] and the mean relative error is 0.6587%. Homogeneous exponent function fitting onetime accumulated generating sequence was used in [5] and it is 0.9765%. Thus, the examples validate the adaptability and the scientific of the proposed model.
4. Conclusion
In this paper, applying the reciprocal accumulated generating and the reconstruction method of GRM(1,1) model’s

Table 1. Relation of Ti alloy fatigue strength (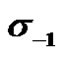 ) along with temperature (T).
) along with temperature (T).
background value of non-equidistant sequence based on the exponential trait of grey model and the integral definition, a novel non-equidistant GRM(1,1) model based on reciprocal accumulated generating was put forward. The Matlab program of this model was written. This model can be used in non-equidistant interval & equidistant interval time series and has the characteristic of high precision as well as high adaptability. Example validates the correctness and validity of the proposed model. There are important practical and theoretical significance and this model should be widely used.
REFERENCES
- Y. X. Luo, L. T. Zhang and M. Li, “Grey Systems and Applications in Mechanical Engineering,” National University of Defense Technology Press, Changsha, 2001.
- Y. X. Luo and J. R. Zhou, “Non-Equidistance GM(1,1) Model and Its Application in Fatigue Experimental Data Processing and On-Line Control,” Journal of Mechanical Strength, Vol. 18, No. 3,1996, pp. 60-63.
- Y. X. Luo, X. Wu and M. Li, “Function-Transfer Method of Parameters Estimation Of Grey GM(1,1) Model and Its Application,” Journal of Mechanical Strength, Vol. 24, No. 3, 2002, pp. 450-452.
- W. Z. Dai and J. F. Li, “Modeling Research on Non-Equidistance GM(1,1) Model,” Systems Engineering Theory & Practice, Vol. 25, No. 9, 2005, pp. 89-93 .
- F. X. Wang, “Improvement on Unequal Interval Gray Forecast Model,” Fuzzy Information and Engineering, Vol. 6, No. 1, 2006, pp.118-123.
- Y. M. Wang, Y. G. Dang and Z. X. Wang, “The Optimization of Background Value in Non-Equidistant GM(1,1) Model,” Chinese Journal of Management Science, Vol. 16, No. 4, 2008, pp. 159-162 .
- Z. M. Song and J. L. Deng, “The Accumulated Generating Operation in Opposite Direction and Its Use in Grey Model GOM(1,1),” Systems Engineering, Vol. 19, No. 1, 2001, pp. 66-69.
- B. H. Yang and Z. Q. Zhang, “The Grey Model Has Been Accumulated Generating Operation in Reciprocal Number and Its Application,” Mathematics in Practice and Theory, Vol. 33, No. 10, 2003, pp. 21-25.
- H. Zhou and X. G. Wang, “A Improvement of the Grey Model GRM(1,1) Generated by Accumulation Generating Operation of Reciprocal Number,” Journal of Shenyang Ligong University, Vol. 27, No. 4, 2008, pp. 84-86.
- D. Y. Xue and Y. Q. Chen, “Solving Applied Mathematical Problems with Matlab,” CRC Press, Inc., Outside North America, 2009.

