Applied Mathematics
Vol. 3 No. 7 (2012) , Article ID: 20011 , 7 pages DOI:10.4236/am.2012.37114
Homotopy Continuous Method for Weak Efficient Solution of Multiobjective Optimization Problem with Feasible Set Unbounded Condition
Department of Mathematics, Harbin Institute of Technology, Harbin, China
Email: xingmeiwei@163.com, mathwby@hit.edu.cn
Received May 9, 2012; revised June 9, 2012; accepted June 16, 2012
Keywords: Multiobjective Optimization Problem; Feasible Set Unbounded; Homotopy Continuous Method; Global Convergence
ABSTRACT
In this paper, we propose a homotopy continuous method (HCM) for solving a weak efficient solution of multiobjective optimization problem (MOP) with feasible set unbounded condition, which is arising in Economical Distributions, Engineering Decisions, Resource Allocations and other field of mathematical economics and engineering problems. Under the suitable assumption, it is proved to globally converge to a weak efficient solution of (MOP), if its x-branch has no weak infinite solution.
1. Introduction
Mathematical modeling of real-life, economics and engineering problems usually results in optimization and decision systems, such as multiobjective optimization systems, linear and nonlinear optimization systems, global optimization systems and others. Many mathematical formulation of economics and decisions contain multiobjective optimization problems, which arise in use of choosing projects in Bid Decision, developing production plan by Enterprise and requiring human resource in Management; for more details see ([1,2]) and the reference cited therein. Therefore, it is very actually meaning subject how we find the KKT points of multiobjective optimization problem. Hence we consider the following multiobjective programming problem with inequality constraints:
(MOP) 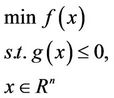
where
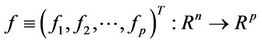
and

are twice times continuously differentiable functions.
Since 1981, Garcia and Zangwill [3] firstly used homotopy method to study convex programming problem, which makes the method become a powerful tool in dealing with various programming problems. In 1988, Megiddo [4] and Kojima [5] et al. discovered that the Karmakar interior point method was a kind of path following method for solving linear programming. Since then the interior path-following method has been extensively used for solving mathematical programming problems. In 1994, Lin, Yu and Feng [6] constructed a new interior point method—combined homotopy interior point method (CHIP method), formed by Newton homotopy and linearly homotopy—for solving the KKT point of convex nonlinear programming. Subsequently, Lin, Li and Yu [7], without strictly convexity of the logarithmic barrier function, showed that the iteration points generated by CHIP, also converged to the KKT points of optimization problem. In 2003, CHIP method was generalized to convex multiobjective optimization problem by Lin, Zhu and Sheng [8]. They constructively proved the existence of KKT system solution for corresponding purification problem.
In 2008, Song and Yao [9] further generalized the results of [8,10]. They constructed a new combined homotopy mapping. A smooth bounded homotopy path was obtained under the normal cone condition and weaker Mangasarian-Fromovitz constraint qualification. However, up till now the convergence of homotopy path in literature related above is obtained under the condition that the feasible set is nonempty and bounded. Recently by adapting the combined homotopy method developed in [11,12], a homotopy method was proposed in [13,14] for variational inequalities on unbounded sets.
In this paper, we will discuss about homotopy methods for MOP on unbounded set. Under conditions which are commonly used in the literature, a smooth path from a given interior point set to a solution of MOP will be proven exist. The paper is organized as follows. In Section 2, we recall some preliminaries results, formulate an equivalent form of KKT system for MOP and list some lemmas from differential topology which will be used in this paper. In Section 3, we proved in detail existence and convergence of the smooth path under a weak condition.
Throughout the paper, let 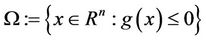 be the feasible set of MOP, and
be the feasible set of MOP, and 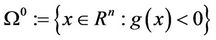 be the strictly feasible set of MOP. In addition, we denote the index set of
be the strictly feasible set of MOP. In addition, we denote the index set of  at x by
at x by
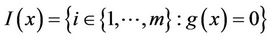 .
.
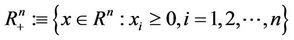
and
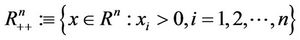
represent the nonnegative and positive orthant of , respectively.
, respectively.
2. Preliminaries
As we know, the solutions for a multiobjective programming problem are referred to variously as efficient, Pareto-optimal and nondominated solution [15]. In this paper, we will refer to a solution of a multiobjective programming problem as an efficient solution.
Definition 2.1 [15] 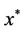 is an efficient solution of multiobjective programming problem, if there is no
is an efficient solution of multiobjective programming problem, if there is no 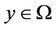 such that
such that 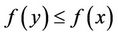 holds.
holds.
In [9], a homotopy method for MOP with bounded 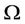 was given. In this paper, we will discuss MOP with
was given. In this paper, we will discuss MOP with 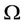 which is not necessarily bounded. It is well known that, if x is an efficient solution of MOP, under some constraint qualifications (e.g. Kuhn and Tucker constraint qualification [16]), MOP satisfies KKT constraint condition at x (see [10,15]):
which is not necessarily bounded. It is well known that, if x is an efficient solution of MOP, under some constraint qualifications (e.g. Kuhn and Tucker constraint qualification [16]), MOP satisfies KKT constraint condition at x (see [10,15]):
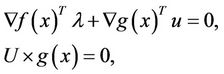 (1)
(1)
where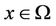 ,
, 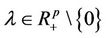 ,
, 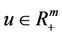 ,
,
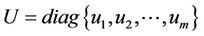 ,
,
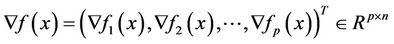
and
 .
.
We call that a point x satisfying the KKT condition (1) is a Karush-Kuhn-Tucker point of MOP, and 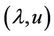 are the corresponding Lagrangian multipliers of MOP at x. Because
are the corresponding Lagrangian multipliers of MOP at x. Because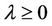 , let
, let 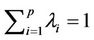 For solving the KKT system, we search a vector
For solving the KKT system, we search a vector
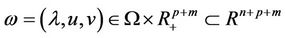
such that
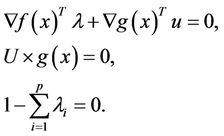 (2)
(2)
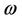 is called a Kuhn-Tucker vector of MOP. Usually, we will solve its KKT system of MOP instead of solving MOP directly.
is called a Kuhn-Tucker vector of MOP. Usually, we will solve its KKT system of MOP instead of solving MOP directly.
The following lemmas from differential topogy will be used in the next section.
Definition 2.2 [17] Let X and Y be topological space, 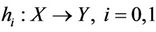 be continuous mapping and
be continuous mapping and  be real interval. H is called a homotopy mapping
be real interval. H is called a homotopy mapping 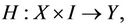 such that
such that
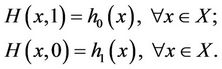
To solve (2), the homotopy mapping H is given by [7] as follow:
 (3)
(3)
where


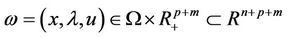
and 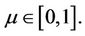 Sometimes, we rewrite
Sometimes, we rewrite 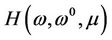 as
as 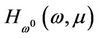 for convenience. Because f and g are continuous mappings, H is also continuous mapping. When
for convenience. Because f and g are continuous mappings, H is also continuous mapping. When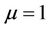 , the homotopy Equation (3) becomes
, the homotopy Equation (3) becomes
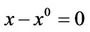 (4)
(4)
 (5)
(5)
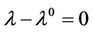 (6)
(6)
Hence, it is easily obtained ,
, 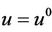 and
and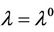 . Thus
. Thus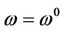 . That is, the equation
. That is, the equation  with respect to
with respect to 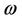 has only one solution.
has only one solution.
As , the solution of the Equation (3) is just that of KKT system (2).
, the solution of the Equation (3) is just that of KKT system (2).
Thus, for a given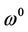 , the zero-point of the mapping
, the zero-point of the mapping  constructed above is the homotopy mapping between the trivial mapping of
constructed above is the homotopy mapping between the trivial mapping of  and KKT system (2) of MOP. To develop our main result, we need the following basic definitions and lemmas in topology. By the definition of Cr differential manifold [17], we know
and KKT system (2) of MOP. To develop our main result, we need the following basic definitions and lemmas in topology. By the definition of Cr differential manifold [17], we know  is a n-dimensional differential manifold. For the definition of product manifold [17],
is a n-dimensional differential manifold. For the definition of product manifold [17],  is a manifold with boundary
is a manifold with boundary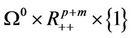 .
.
Definition 2.3 [17] Let U, V be differential manifold with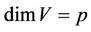 , and
, and 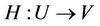 be a differential mapping. We say that
be a differential mapping. We say that 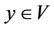 is a regular value of H and
is a regular value of H and 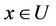 is a regular point, if
is a regular point, if
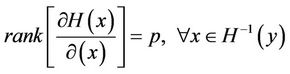 (7)
(7)
holds. Given a curve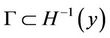 , if every
, if every  is a regular point, then
is a regular point, then 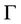 is a regular path.
is a regular path.
Lemma 2.1 [17] Let 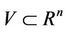 and
and 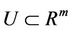 be two open sets, and
be two open sets, and 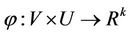 be a
be a 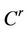 differentiable mapping with
differentiable mapping with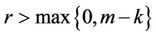 . If
. If 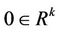 is a regular value of
is a regular value of , then for almost all
, then for almost all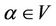 , 0 is a regular value of
, 0 is a regular value of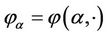 .
.
Lemma 2.2 [17] If 0 is a regular value of the mapping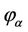 , then
, then 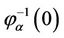 consists of some smooth manifolds.
consists of some smooth manifolds.
Lemma 2.3 (Classification Theorem of One-Dimensional Manifold with Boundary [17]) Each connected part of a one-dimensional manifold with boundary is homeomorphic either to a unit circle or to a unit interval.
3. Main Results
According to [15], as the objective function of optimization problem is convex, there exists a  and
and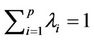 , satisfying
, satisfying 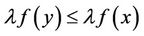 for any weak efficient solution x of MOP. Thus, we introduce the definition of a weak solution at infinity for MOP.
for any weak efficient solution x of MOP. Thus, we introduce the definition of a weak solution at infinity for MOP.
Definition 3.1 MOP has a weak solution at infinity, denoted by a sequence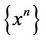 , if
, if 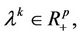
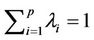 ,
, 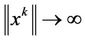
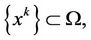 as
as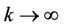 , and for any given
, and for any given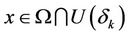 , there exist
, there exist 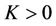 and
and 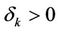 such that
such that 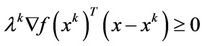 as
as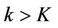 , where
, where 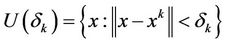 .
.
The following example illustrates the meaning of Definition 3.1.
Example 3.1 Consider MOP with 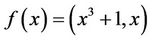
and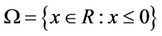 . Take
. Take 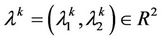 and
and
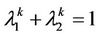 . Let
. Let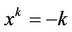 ,
, . Then
. Then 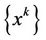 is a weak solution at infinity for MOP as
is a weak solution at infinity for MOP as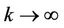 . For any given
. For any given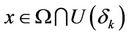 , there exist
, there exist 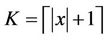 and
and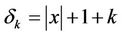 , when
, when 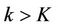 satisfying
satisfying
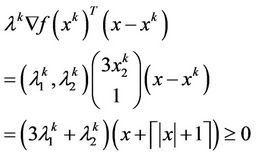
Theorem 3.1 Consider the homotopy mapping H of MOP constructed as (3). Suppose the following four conditions are satisfied:
(A) 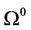 is nonempty (Slater condition);
is nonempty (Slater condition);
(B) For any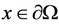 ,
, 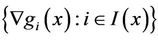 are nonnegatively independent, i.e.
are nonnegatively independent, i.e. 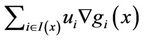 and
and 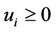
for any 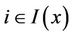 imply that
imply that 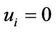 for any
for any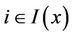 ;
;
(C) 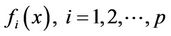 and
and 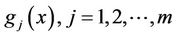 are twice continuously differentiable functions. All of
are twice continuously differentiable functions. All of 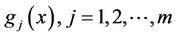 are convex;
are convex;
(D) There exist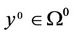 , such that
, such that
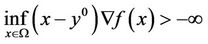 and MOP has weak solution at infinity.
and MOP has weak solution at infinity.
Then, for almost all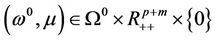 , the zero-point set
, the zero-point set 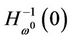 of the homotopy map (3) contains a smooth curve
of the homotopy map (3) contains a smooth curve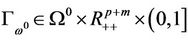 , which starts from
, which starts from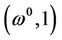 . As
. As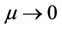 , the limit set
, the limit set
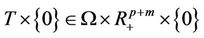 of
of  is nonempty and every point
is nonempty and every point 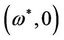 in
in 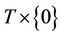 is a solution of KKT system (2).
is a solution of KKT system (2).
To prove Theorem 3.1, we need to prove the following three results. For a given , we set
, we set
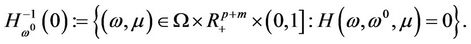
Lemma 3.1 If the conditions (A) and (B) of Theorem 3.1 holds, then for almost all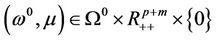 0 is a regular value of
0 is a regular value of 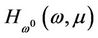 and
and 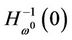 consists of some smooth curves. Among them, a smooth curve
consists of some smooth curves. Among them, a smooth curve 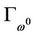 starts from
starts from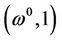 .
.
Proof: For any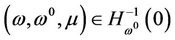 ,
,
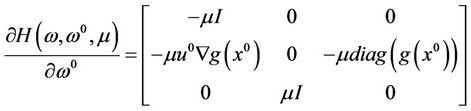
where I is an identical matrix. By a simple computation, we have
 .
.
For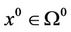 , we have
, we have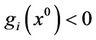 , and hence
, and hence
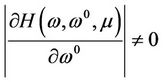 . Thus, 0 is the regular value of H. By Lemma 2.1, for almost all
. Thus, 0 is the regular value of H. By Lemma 2.1, for almost all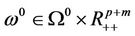 , 0 is a regular value of
, 0 is a regular value of . By Lemma 2.2,
. By Lemma 2.2, 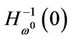 consists of some smooth curves. Since
consists of some smooth curves. Since 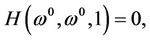 there must be a smooth curves, denoted by
there must be a smooth curves, denoted by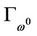 , which starts from
, which starts from 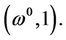
Lemma 3.1 guarantees that the zero-point set of H has a good geometric structure. The following theorem is the key of boundedness for the homotopy path generated by (3), which is the main result of this paper.
Theorem 3.2 Suppose that the condition (C) of Theorem 3.1 holds. There exists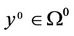 , such that
, such that
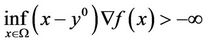 . Then, either the x-component of the smooth curve
. Then, either the x-component of the smooth curve 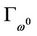 is bounded or (2) has a weak solution at infinity.
is bounded or (2) has a weak solution at infinity.
Proof: For any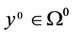 , we construct two set as follows:
, we construct two set as follows:


Thus, we have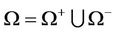 .
.
The properties of norm imply the following equality holds, that is, given a start point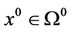 , for any
, for any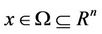 , we have
, we have
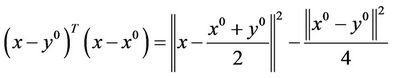 .
.
Indeed
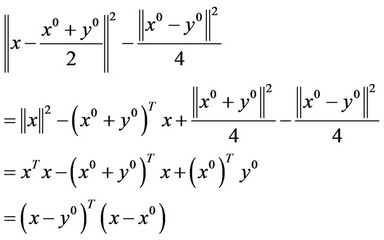
Take any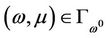 . From the first Equation (3) multiplied by
. From the first Equation (3) multiplied by , we obtained that
, we obtained that
 (8)
(8)
By the convexity of 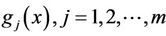 and
and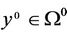 , we know:
, we know:
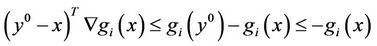 (9)
(9)
From the (7), (8) and the second equation in (3), we simplify the Equation (8), that is
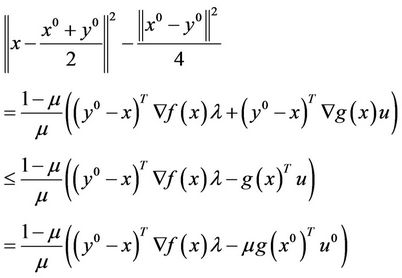
Taking  and
and , we have
, we have
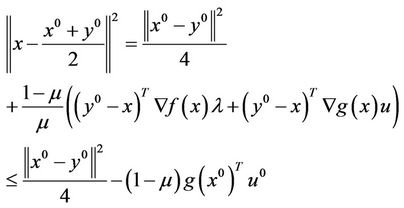
Hence, 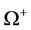 is bounded.
is bounded.
Suppose that x-component of 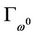 is unbounded, there exists
is unbounded, there exists 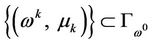 such that
such that
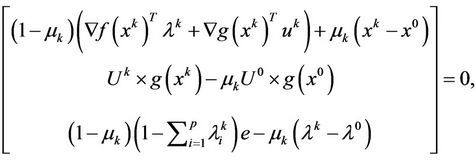 (10)
(10)
and 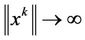 as
as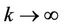 . Without loss of generality, suppose that
. Without loss of generality, suppose that 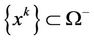 by boundedness of
by boundedness of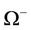 , from the equality (7), (10),
, from the equality (7), (10),  and
and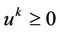 , we obtained that for any
, we obtained that for any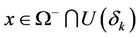 ,
,
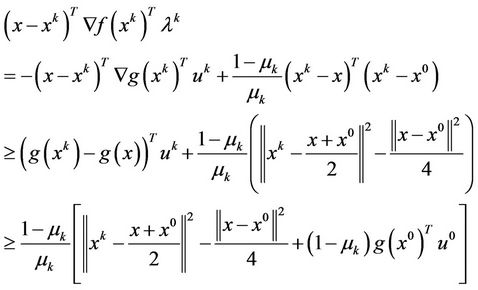
As 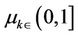 and
and 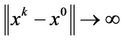 as
as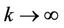 , hence, for any sufficient large k, there exists
, hence, for any sufficient large k, there exists 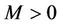 such that
such that
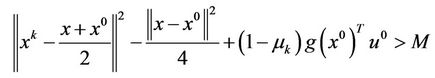
Therefore, 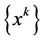 is a weak solution at infinity to MOP by Definition 3.1.
is a weak solution at infinity to MOP by Definition 3.1.
If MOP has no weak solution at infinity, the x-component of 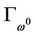 is a bounded curve from Theorem 3.2. Refer to [8], we know that
is a bounded curve from Theorem 3.2. Refer to [8], we know that 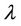 -component in
-component in 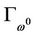 is also bounded curve. Thus, we only need to prove that u-component in
is also bounded curve. Thus, we only need to prove that u-component in 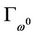 is bounded, in order to obtain that
is bounded, in order to obtain that  is a bounded curve.
is a bounded curve.
Theorem 3.3 (Boundedness) Suppose that the condition (A)-(D) of Theorem 3.1 hold. For a given
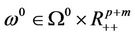 , if 0 is a regular value of
, if 0 is a regular value of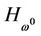 , then
, then  is a bounded curve in
is a bounded curve in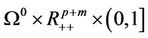 .
.
Proof: We use proof by contradiction. Suppose that 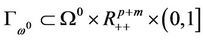 is bounded. Then, by Theorem 3.2 there exists a sequence
is bounded. Then, by Theorem 3.2 there exists a sequence 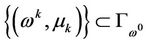 such that
such that
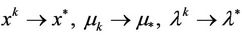 and
and 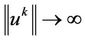 as
as 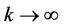
From the second equality of (10), we obtain that there exists some index i such that
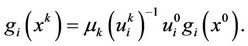 (11)
(11)
Since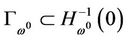 , let
, let
 where
where 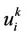 denotes the ith component of
denotes the ith component of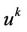 . Hence,
. Hence, 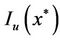 is nonempty. It follows from (11) that
is nonempty. It follows from (11) that 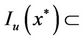
 , that is
, that is 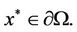 From the first equality of (10),
From the first equality of (10),
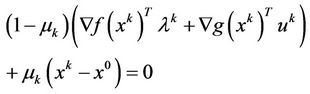 (12)
(12)
The following is divided two parts:
1) When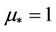 , rewrite (12) as
, rewrite (12) as
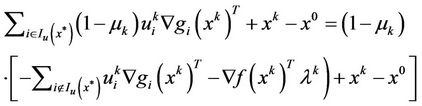
Let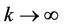 ; Since
; Since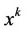 ,
,  and
and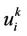 ,
, 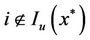 are all bounded, the above equality becomes
are all bounded, the above equality becomes
 (13)
(13)
From the condition (C), 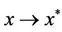 implies
implies 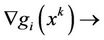
 . Hence (13) becomes
. Hence (13) becomes
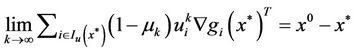 . (14)
. (14)
It is obviously that the coefficient in left-hand side
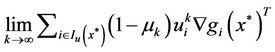
of equality (14) must be positive finite quantities as value. Otherwise, the condition (B) of Theorem 3.1 implies
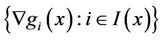 is nonnegatively independent, i.e.
is nonnegatively independent, i.e. 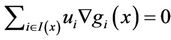 and
and 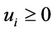 for any
for any 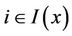 imply that
imply that  for any
for any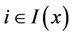 . So, if we take
. So, if we take 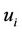 as infinite value,
as infinite value,  holds. Therefore, if we get
holds. Therefore, if we get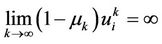 ,
, 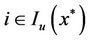 , the lefthand side of equality (14) is infinite. This is contradiction with the finite value of the right-hand for the equality
, the lefthand side of equality (14) is infinite. This is contradiction with the finite value of the right-hand for the equality
(14). Let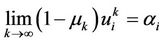 ,
, 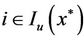 , where
, where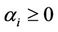 . Hence we have
. Hence we have
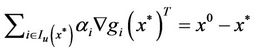 (15)
(15)
Since 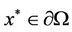 and
and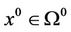 , the equality (15) multiplied by
, the equality (15) multiplied by  implies:
implies:
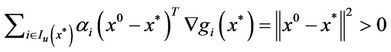 (16)
(16)
However, the convexity of 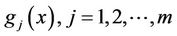 implies
implies
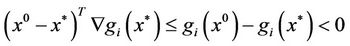
Thus, we obtain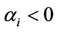 . This contradicts
. This contradicts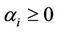 . So
. So 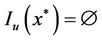 as
as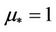 .
.
2) When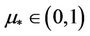 , we rewrite (12) as
, we rewrite (12) as
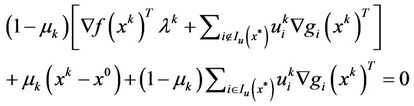 (17)
(17)
From 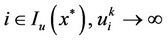 and the condition (B), it follows that the last term in the (17) tends to infinity, whereas the first and second terms are bounded. This is impossible.
and the condition (B), it follows that the last term in the (17) tends to infinity, whereas the first and second terms are bounded. This is impossible.
As stated previously, 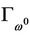 is a smooth bounded curve.
is a smooth bounded curve.
Proof of Theorem 3.1: By Lemma 2.3, 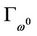 must be diffeomorphic to a unit circle or a unit interval
must be diffeomorphic to a unit circle or a unit interval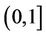 .
.
Since the matrix

Is nonsingular, 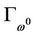 is not tangent to the plane
is not tangent to the plane  at
at . Because
. Because 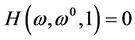 has only one solution
has only one solution , we know
, we know 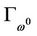 must have limit point. We assume that
must have limit point. We assume that 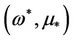 is limit point, then
is limit point, then
 .
.
In fact, if
 since 0 is a regular value of
since 0 is a regular value of 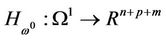 and
and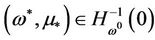 , the Jacobian matrix of H at
, the Jacobian matrix of H at 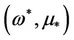
is full row rank. By implicit function theorem, 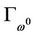 must be extended at
must be extended at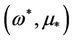 . This contradicts the fact that
. This contradicts the fact that 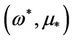 is a limit point of
is a limit point of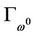 . Hence only the following three cases are possible:
. Hence only the following three cases are possible:
1)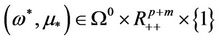 ;
;
2)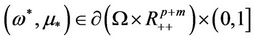 ;
;
3) 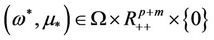
Case 1) is impossible because 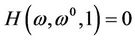 has only one solution
has only one solution  in
in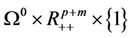 .
.
Case 2) holds, which implies that there must be a sequence 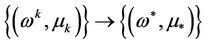 as
as  in
in  and
and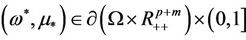 . However, in fact, the component
. However, in fact, the component 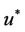 and
and 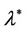 in
in 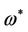 satisfying
satisfying 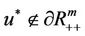 and
and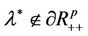 .
.
Indeed, if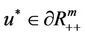 , then there must be some
, then there must be some  satisfying
satisfying . So there exists a sequence
. So there exists a sequence
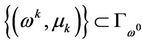 such that
such that 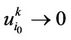 as
as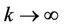 . Since
. Since 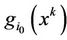 is bounded, we have
is bounded, we have 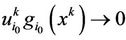
 .
.
From the second equality of homotopy Equation (10), we can see
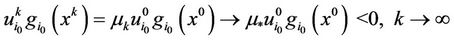 .
.
This is a contradiction.
Second, we assume that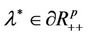 . There also exists a sequence
. There also exists a sequence 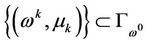 such that
such that 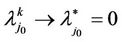
as 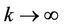 for some
for some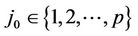 . Noticing that
. Noticing that 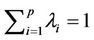 and from the third equality in (10), we have
and from the third equality in (10), we have
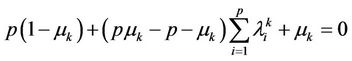 .
.
As , since
, since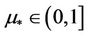 , we obtain
, we obtain  from the above equation. Take the
from the above equation. Take the 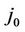 th equality of the third equation in (10),
th equality of the third equation in (10),
 .
.
Let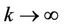 , we can see
, we can see 
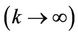 . Thus
. Thus 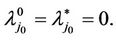 This contradicts
This contradicts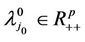 . Hence case 2) does not hold.
. Hence case 2) does not hold.
Therefore case 3) is the only possible case. From Theorem 3.3 and condition (D), 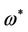 is a solution of the KKT system.
is a solution of the KKT system. 
Remark 3.1 If 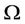 is a bounded set, the condition (D) of Theorem 3.1 holds obviously. Hence, the result of Theorem 3.1 implies the one in [9].
is a bounded set, the condition (D) of Theorem 3.1 holds obviously. Hence, the result of Theorem 3.1 implies the one in [9].
Above all, we do not only prove the existence of solution for KKT equation, but also give a kind of numerical algorithm, that is, the solution can be obtained by tracing numerically the homotopy path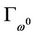 , starting from
, starting from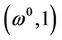 . If we denote s as arc length parameter of curve
. If we denote s as arc length parameter of curve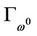 , then the differential homotopy Equation (1) with respect to s implies the theorem as follow:
, then the differential homotopy Equation (1) with respect to s implies the theorem as follow:
Theorem 3.4 Assume that the conditions (A)-(D) in Theorem 3.1 hold. We denote 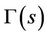 as parametrized curve of
as parametrized curve of , where s represents arc length parameter of
, where s represents arc length parameter of . Then
. Then 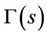 is determined by the following initial value problem to the ordinary differential equation:
is determined by the following initial value problem to the ordinary differential equation:
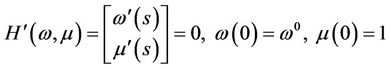 (18)
(18)
If there exists 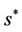 such that
such that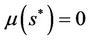 , then
, then 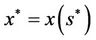 ,
, 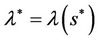 and
and 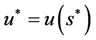 are the solution of KKT equation.
are the solution of KKT equation.
4. Conclusion
In summary, the HCM is employed to find weak efficient of MOP with inequality constraints. The method needs much less restrictive condition and computational work compared with traditional method. It is shown that the HCM is globally convergent and computational tractability for solving MOP on unbounded set.
5. Acknowledgements
The authors are grateful to Professor W. Song and the referee for valuable comments and suggestions. We also thank editors and reviewers for their valued comments, which helped in improving the quality of the paper.
REFERENCES
- A. Charne and W. W. Cooper, “Management Models and Industrial Application of Linear Programming,” Wiley Press, New York, 1961.
- G. Fandel and T. Gal, “Multiple Criteria Decision Making: Theory and Applications,” Springer-Verlag Press, New York, 1980. doi:10.1007/978-3-642-48782-8
- C. B. Garcia and W. I. Zangwill, “Pathways to Solutions, Fixed Points and Equilibria,” Prentice-Hall, Englewood Cliffs, 1981, pp. 475-495.
- N. Megiddo, “Pathways to the Optimal Set in Linear Programming,” In: N. Megiddo, Ed., Progress in Mathematical Programming Interior Point and Related Methods, Springer, New York, 1988, pp. 131-158.
- M. Kojima, S. Mizuno and A. Yoshise, “A Primal-Dual Interior Point Algorithm for Linear Programming,” In: N. Megiddo, Ed., Progress in Mathematical Programming Interior Point and Related Methods, Springer, New York, 1988, pp. 29-47.
- Z. H. Lin, B. Yu and G. C. Feng, “A Combined Homotopy Interior Point Method for Convex Nonlinear Programming Problems,” Applied Mathematics and Computation, Vol. 84, No. 2-3, 1994, pp. 193-211. doi:10.1016/S0096-3003(96)00086-0
- Z. H. Lin, Y. Li and B. Yu, “A Combined Homotopy Interior Point Method for General Nonlinear Programming Problems,” Applied Mathematics and Computation, Vol. 80, No. 2-3, 1997, pp. 209-224. doi:10.1016/0096-3003(95)00295-2
- Z. H. Lin, D. L. Zhu and Z. D. Sheng, “Finding a Minimal Efficient Solution of a Convex Multiobjective Program,” Journal of Optimization Theory and Applications, Vol. 118, No. 3, 2003, pp. 587-600. doi:10.1023/B:JOTA.0000004872.93803.09
- W. Song and G. M. Yao, “Homotopy Method for a General Multiobjective Programming Problem,” Journal of Optimization Theory and Applications, Vol. 138, No. 1, 2008, pp. 139-153. doi:10.1007/s10957-008-9366-6
- T. Maeda, “Second-Order Conditions for Efficiency Nonsmooth Multiobjective Optimization Problems,” Journal of Optimization Theory and Applications, Vol. 122, No. 3, 2004, pp. 521-538. doi:10.1023/B:JOTA.0000042594.46637.b4
- L. T. Watson, “Globally Convergent Homotopy Algorithms for Nonlinear Systems of Equations,” Nonlinear Dynamics, Vol. 1, No. 2, 1990, pp.143-191. doi:10.1007/BF01857785
- G. C. Feng, Z. L. Lin and B. Yu, “Existence of an Interior Pathway to a Karush-Kuhn-Tucker Point of a Nonlinear Programming Problem,” Nonlinear Analysis, Vol. 32, No. 6, 1998, pp. 761-768. doi:10.1016/S0362-546X(97)00516-6
- Q. Xu, B. Yu and G. C. Feng, “Homotopy Methods for Solving Variational Inequalities in Unbounded Sets,” Journal of Global Optimization, Vol. 31, No. 1, 2005, pp. 121-131. doi:10.1007/s10898-004-4272-4
- Q. Xu, B. Yu, G. C. Feng and C. Y. Dan, “Condition for Global Convergence of a Homotopy Method for Variational Inequality Problems on Unbounded Sets,” Optimization Methods and Software, Vol. 22, No. 4, 2007, pp. 587-599. doi:10.1080/10556780600887883
- C. Y. Lin and J. L. Dong, “Methods and Theories in Multiobjective Optimization,” Jilin Education Press, Changchun, 1992.
- H. W. Kuhn and A. W. Tucker, “Nonlinear Programming,” Proceedings of the Second Berkeley Symposium on Mathematical Statistics and Probability, University of California Press, Berkeley, 1951.
- G. L. Naber, “Topological Methods in Euclidean Space,” Cambridge University Press, London, 1980.

