ABSTRACT

In this paper, we study the k-Lucas numbers of arithmetic indexes of the form an + r, where n is a natural number and r is less than r. We prove a formula for the sum of these numbers and particularly the sums of the first k-Lucas numbers, and then for the even and the odd k-Lucas numbers. Later, we find the generating function of these numbers. Below we prove these same formulas for the alternated k-Lucas numbers. Then, we prove a relation between the k-Fibonacci numbers of indexes of the form 2^rn and the k-Lucas numbers of indexes multiple of 4. Finally, we find a formula for the sum of the square of the k-Fibonacci even numbers by mean of the k-Lucas numbers.

1. Introduction

Let us remember the k-Lucas numbers L_k,n are defined [1] by the recurrence relation with the initial conditions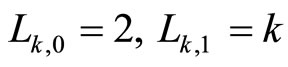

Among other properties, the Binnet Identity establishes being and 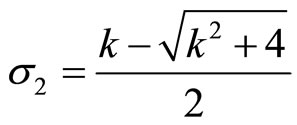the characteristic roots of the recurrence equation.

Evidently,.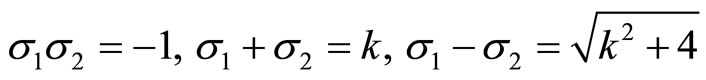

Moreover, it is verified [1, Theorem 2.4] that.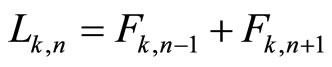

If we apply iteratively the equation 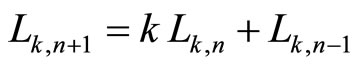then we will find a formula that relates the k–Lucas numbers to the k–Fibonacci numbers:

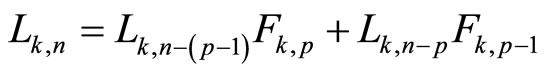(1.1)

This formula is similar to the Convolution formula for the k–Fibonacci numbers [2,3].

Moreover, we define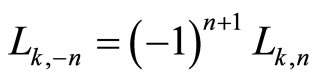. Then, if we do p = −n in Formula (1.1) obtain

.

2. On the k-Lucas Numbers of Arithmetic Index

We begin this section with a formula that relates each other some k-Lucas numbers.

2.1. Theorem 1 (The k-Lucas Numbers of Arithmetic Index)

If a is a nonnull natural number and r = 0, 1, 2, ... a − 1, then

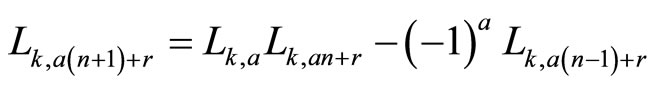(2.1)

Proof. In [4] it is proved

.

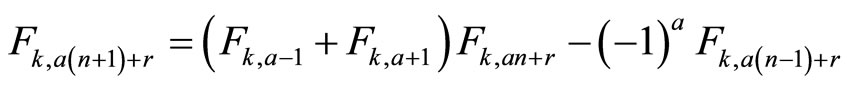Then

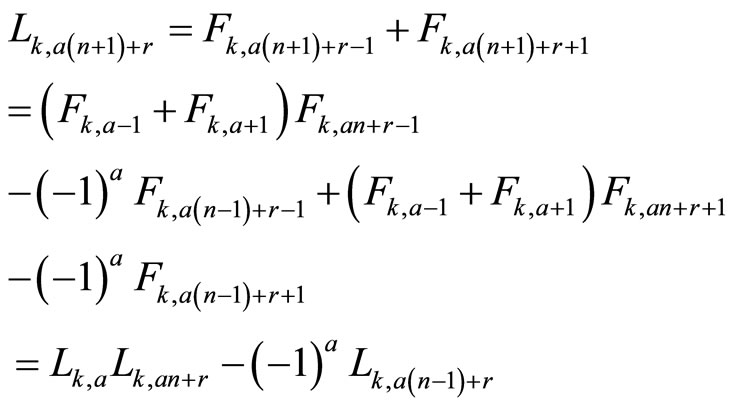
If r = 0, then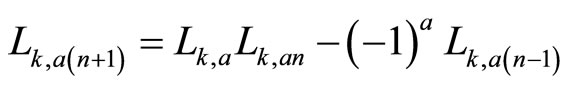

In this case, if a = 2p + 1, then an odd k-Lucas number can be expressed in the form

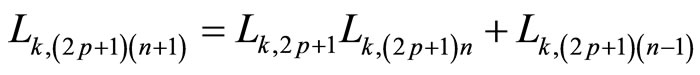
Applying iteratively Formula (2.1), the general term, for, can be written like a non-linear combination of the form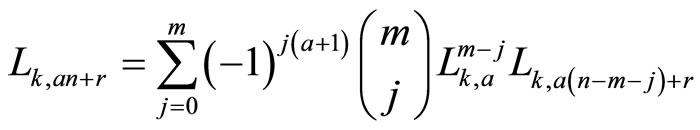

In particular, if m = n, then

2.2. Generating Function of the Sequence {L_{k, an + r}}

Let 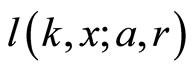be the generating function of the sequence. That is,

Then,

and

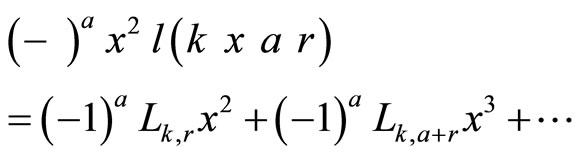
from where no more to take into account Formula (2.1). So, the generating function of the sequence is

.

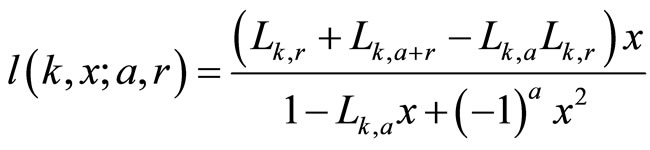As particular case, if a = 1, then r = 0 and the generating function of the k-Lucas sequence is 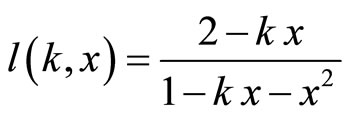, that, for the classical Lucas sequence is

If we want to take out the two bisection sequences of the classical Lucas sequence (k = 1), the respective generating functions are a = 2 and r = 0: 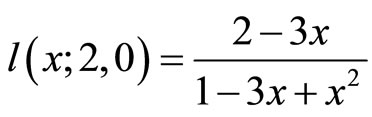that generates the sequence a = 2 and r = 1: 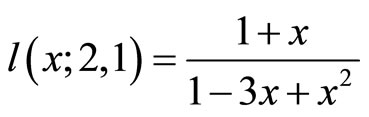that generates the sequence.

2.3. Theorem 2 (Sum of the k-Lucas Numbers of Arithmetic Index)

If a is a nonnull natural number and r = 0, 1, 2, ... a − 1, then

(2.2)

Proof.

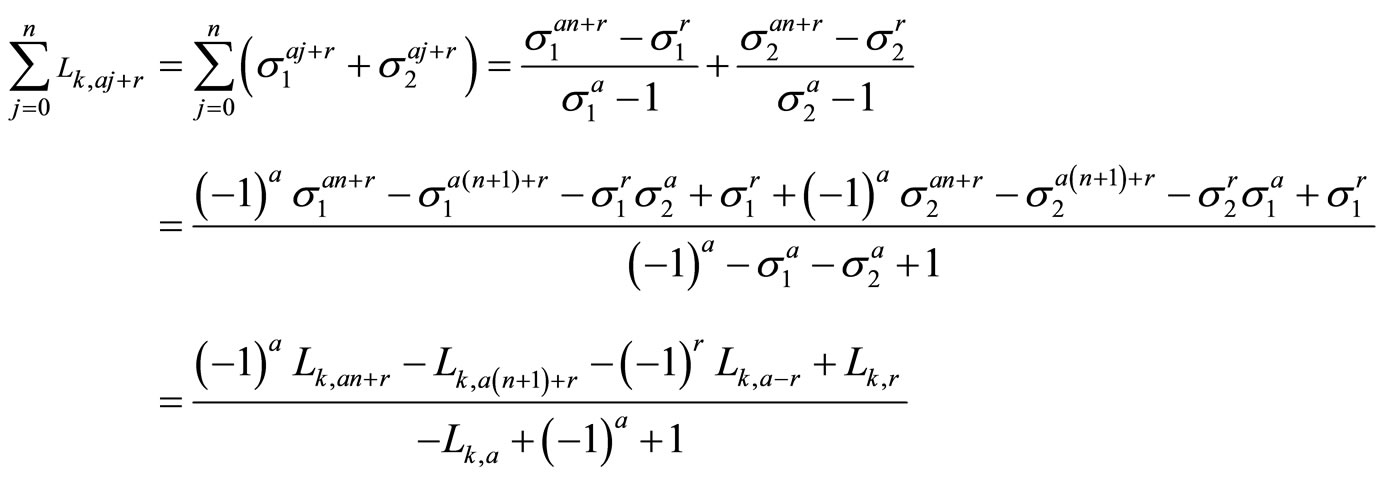
because

and after applying the formula for the sum of a geometric progression.

2.4. Corollary 1 (Sum of Consecutive Odd k-Lucas Numbers)

If r = 0 and a = 2p + 1, Equation (2.2) is

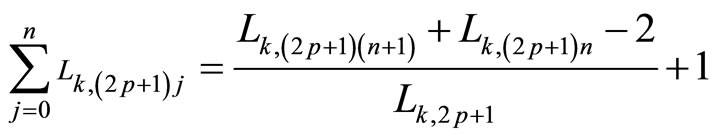
In this case, the sum of the first k-Lucas numbers is (for p = 0),

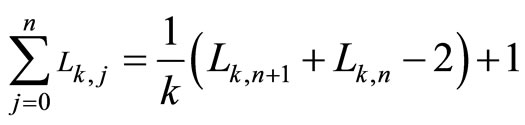(2.3)

that for the classical Lucas numbers is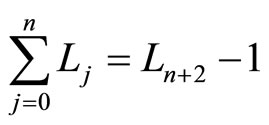

2.5. Corollary 2 (Sum of Consecutive Even k-Lucas Numbers)

If r = 0 and a = 2p, then Equation (2.2) is

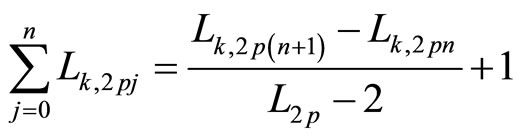(2.4)

In this case, if p = 1 we obtain the formula for the sum of the first even k-Lucas numbers, and for the classical Lucas numbers is

2.6. Theorem 3 (Sum of Alternated k-Lucas Numbers of Arithmetic Index)

For a > 0 and r = 0, 1, 2, ...a − 1, the sum of alternated k-Lucas numbers is

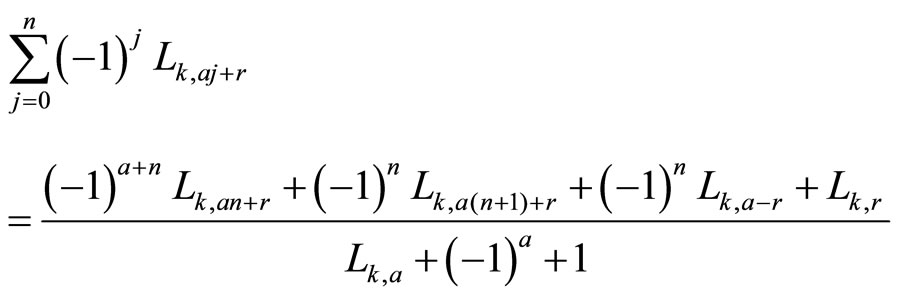
Proof. As in the previous theorem,

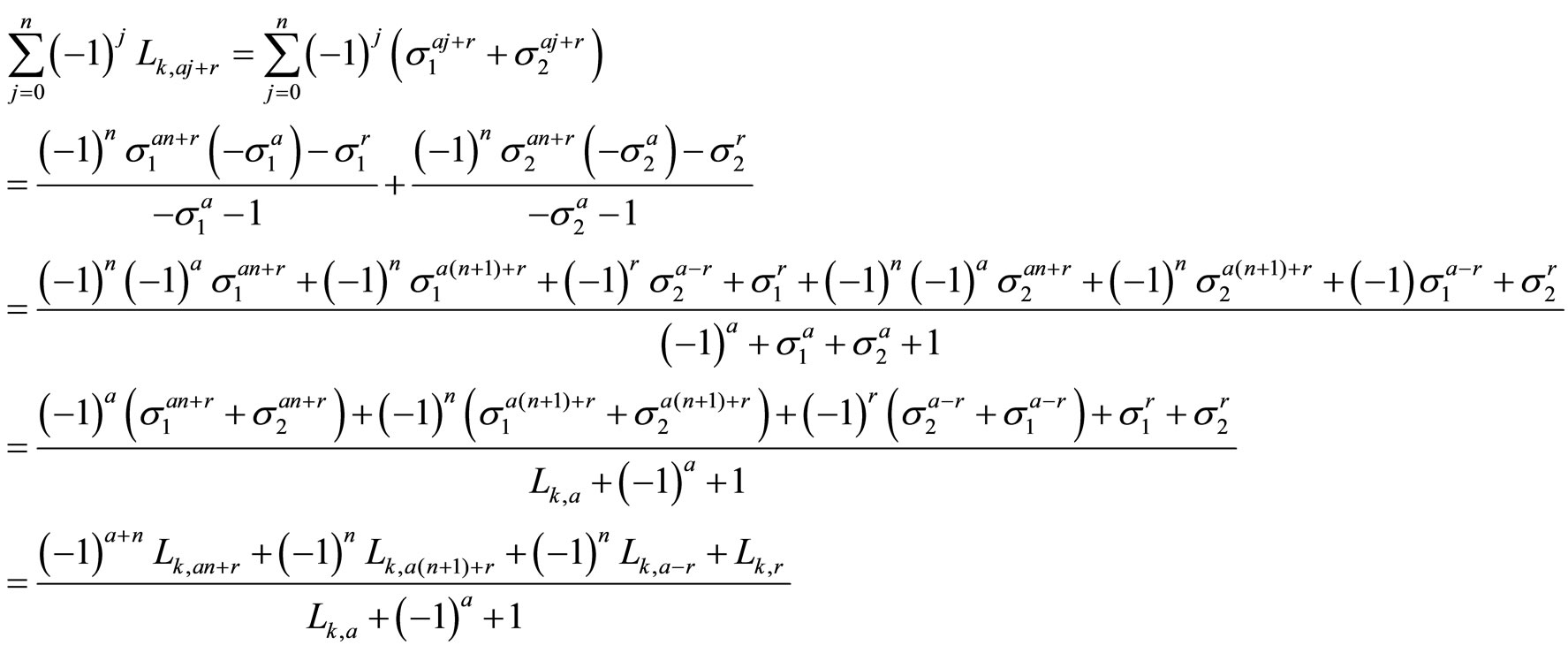
2.7. Corollary 3 (Sum of Consecutive Alternated Odd k-Lucas Numbers)

As particular case, if a = 2p + 1 and r = 0,

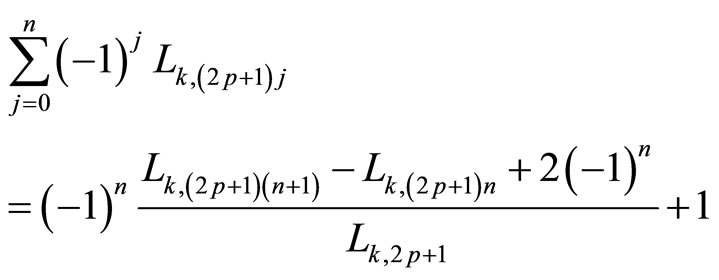
Then, for p = 0 we obtain the sum of the first alternated k-Lucas numbers

, that for the classical Lucas numbers is

.

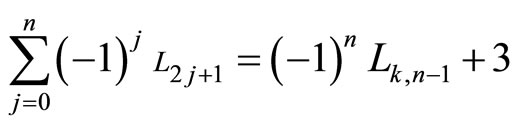2.8. Corollary 4 (Sum of Consecutive Alternated Even k-Lucas Numbers)

If r = 0 and a = 2p + 1, then

And for the first consecutive alternated even k-Lucas numbers

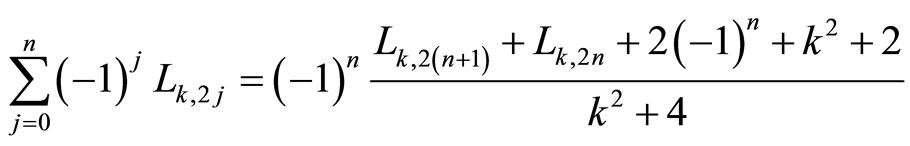that for the classical Lucas numbers is

.

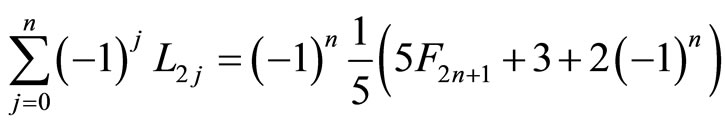3. On the k-Fibonacci Numbers of Indexes n and the k-Lucas Numbers

In this section we will study a relation between the numbers 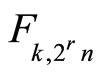and.

3.1. Theorem 4 (A Relation between Some k-Fibonacci and the k-Lucas Numbers)

For r ≥ 1, it is

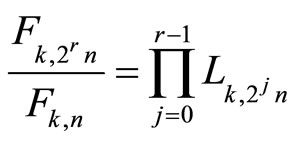(3.1)

Proof.

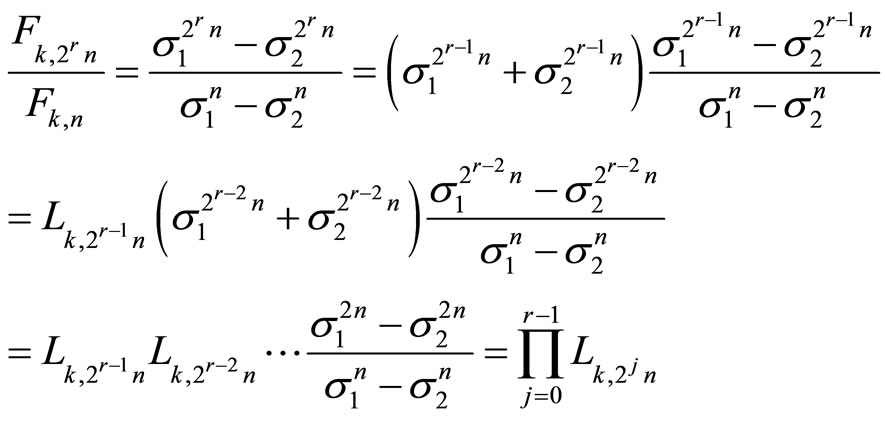
In particular, if r = 1, it is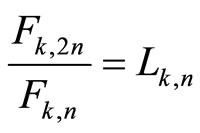

Taking into account, if we expand Formula (3.1), we find that this formula can be expressed as 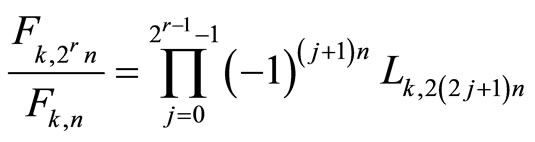or, that is the same,

Then, applying Formula (2.2) to the second hand right of this equation with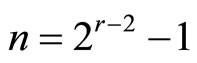, a = 4n, and r = 3n for the first term and r = n for the second,

(3.2)

We tray to simplify the second hand right of this equation. For that, we will prove the following Lemma.

3.2. Lemma 1

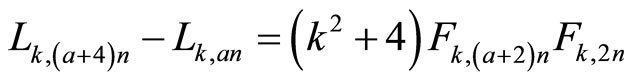(3)

Proof. We will apply the following formulas:

(relation)

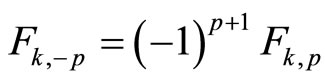(negative)

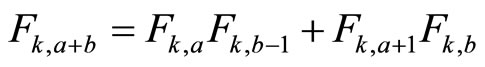(convolution)

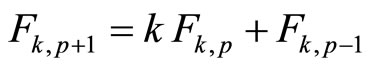(definition)

Then:

(by relation)

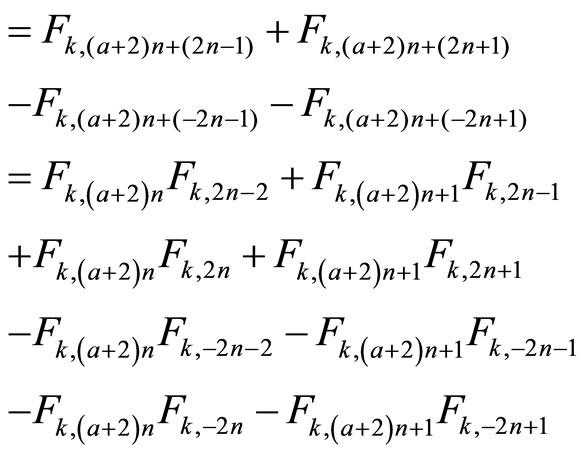(by convolution)

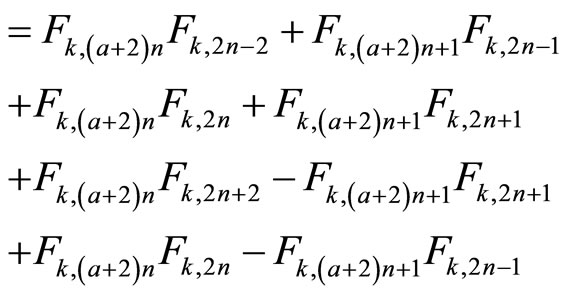(by negative)

(by definition)

And applying this Lemma to Equation (3.2), we will have:

that is

from where

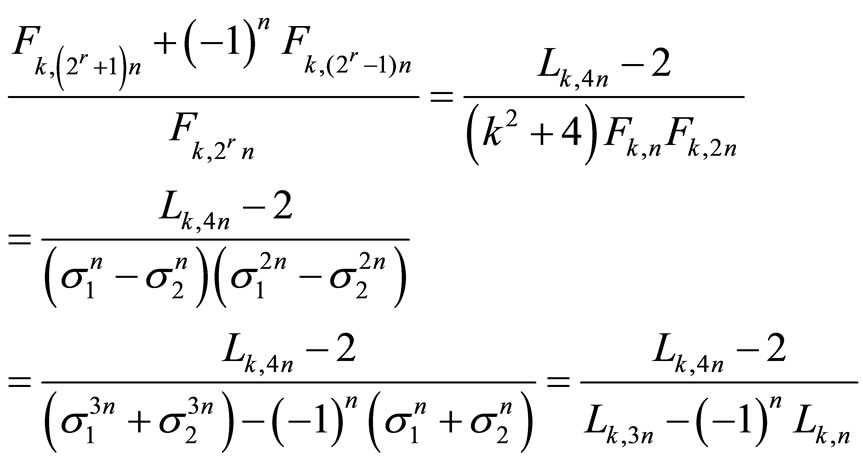
If in Equation (3.3) it is a = 0, then it is , and applying the Formulas (2.5) and (2.4),

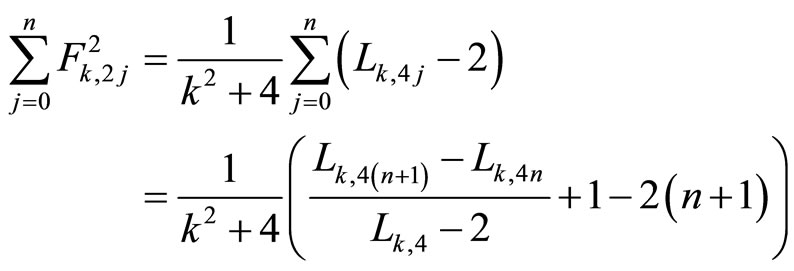
That is

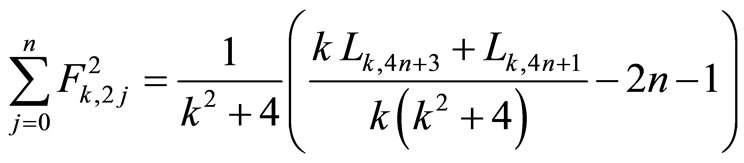
In particular, for the classical Lucas numbers (k = 1), it is.

4. Acknowledgements

This work has been supported in part by CICYT Project number MTM200805866-C03-02 from Ministerio de Educación y Ciencia of Spain.

REFERENCES