Applied Mathematics
Vol. 3 No. 1 (2012) , Article ID: 16759 , 6 pages DOI:10.4236/am.2012.31014
Interaction between Dutch Soccer Teams and Fans: A Mathematical Analysis through Cooperative Game Theory
Faculty of Electrical Engineering and Mathematics and Computer Science, University of Twente, Enschede, The Netherlands
Email: dshhou@126.com
Received October 5, 2011; revised November 30, 2011; accepted December 8, 2011
Keywords: Club Positioning Matrix 2011; Dutch soccer; fan data cost game; nucleolus
ABSTRACT
Inspired by the first lustrum of the Club Positioning Matrix (CPM) for professional Dutch soccer teams, we model the interaction between soccer teams and their potential fans as a cooperative cost game based on the annual voluntary sponsorships of fans in order to validate their fan registration in a central database. We introduce a natural cost allocation to the soccer teams, based in a natural manner on the sponsorships of fans. The game theoretic approach is twofold. On the one hand, an appropriate cost game called “fan data cost game” is developed and on the other, it is shown that the former natural cost allocation agrees with the solution concept called “nucleolus” of the fan data cost game.
1. Club Positioning Matrix (CPM) of Professional Dutch Soccer
Five years CPM. The first lustrum of the (Dutch) “Eredivisie Effectenbeurs”is a fact. At the initiative of the professional teams in the Dutch soccer league called “Eredivisie”, the first CPM research has been carried out October 2006 by one of the German leading research and consultancy companies in international sport business (i.e., marketing and sponsoring) called “Sport + Markt” (www.sportundmarkt.com). October 2009 the fourth CPM research involved 4.500 participants randomly selected from the whole Dutch population (with the common feature to be a fan of soccer). Since these eighteen soccer teams were not satisfied at all by the point of time October, the fifth CPM research edition has been carried out among 4.500 participants in two stages, namely August 2010 at the beginning of the soccer season and January 2011 during the soccer winter break. The end of March 2011, the CPM 2011 scores have been sent to the professional Dutch soccer teams and published exclusively in the weekly Dutch soccer magazine “Voetbal International” (www.vi.nl) [1].
The CPM 2011 scores have direct consequences for the participating soccer teams since the allocation of media (television and broadcast) money among all the soccer teams is based equally on both the annual sport results and the average CPM scores over three years. The more CPM points, the more media money. During one half of a century, the annual sport results were dominated fully by the triple PSV Eindhoven (last Dutch championships in 2000, 2001, 2003, 2005, 2006, 2007, 2008), Ajax Amsterdam (2002, 2004, 2011), and Feyenoord Rotterdam (1974, 1984, 1993, 1999), with exceptions caused by DWS in 1964, AZ'67 Alkmaar in 1981 as well as 2009, and FC Twente Enschede in 2010. The top five of the last three annual sport results are listed in Table 1.
The annual CPM is a marketing instrument that measures the marketing value (through a professional jury of marketing specialists) as well as the imago of every professional soccer team (through the randomly selected soccer fans), which, in turn, is determined on the basis of six parts. Finally, the marketing value, the imago, and the annual sport result are put into some calculation model yielding the annual CPM scores.
The top five of the best marketing is as follows: 1) PSV; 2) SC Heerenveen; 3) FC Twente; 4) Ajax; 5) Feyenoord. Like the fourth edition, the team with the best imago is FC Twente due to its unique national championship, its successful participation in the international Champions League as well as the European League (till the quarter finales), and its new stadium called Grolsch Veste. FC Twente’s imago is the best in the subfields attraction (charm), fascination, economical success, and the second best in the subfields emotional involvement and identification. The top six of the best imago is as follows: 1) FC Twente 699; 2) Ajax 641; 3) PSV 624; 4) SC Heerenveen 558; 5) FC Groningen 539; 6) Feyenoord 476.
In summary, the CPM score of FC Twente increased drastic, Feyenoord’s score decreased drastic, so that the third ranking in the CPM 2011 scores is occupied by FC
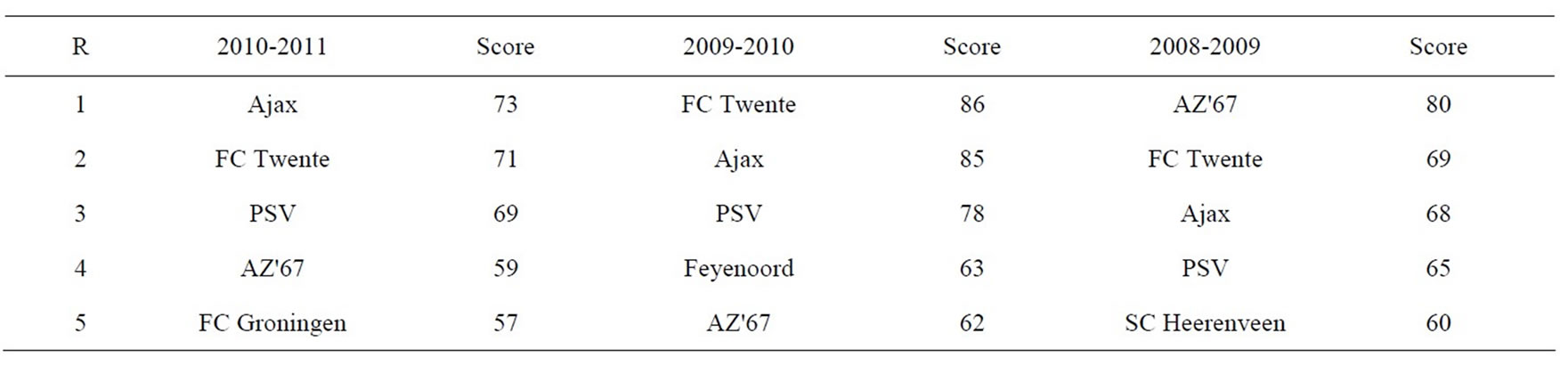
Table 1. The top five of the last three annual sport results is as follows (R = ranking).
Twente. Ajax and PSV remain first and second due to the CPM results of the previous years. The top seven of the last three final CPM rankings are listed in Table 2.
Concerning the fanstatus, the CPM 2011 top five is as follows: 1) Ajax; 2) Feyenoord; 3) PSV; 4) FC Twente; 5) AZ’67. During the first CPM research October 2006, FC Twente started with a fanstatus of 250.000 fans, nowadays its fanstatus has been increased up to about 1.6 million, being the double of its previous edition.
2. The Fan Database Model
Given the current fan status as the model of the interaction between the professional Dutch soccer teams and their potential fans, our main goal is to apply the solution part of the mathematical field called “cooperative game theory”. The so-called “players” are the soccer teams, each of which is endowed with a set of potential fans, each of which is supposed to validate its fan registration in a central database through an annual voluntary sponsorship to be cashed to the national soccer association. This annual sponsorship is said to be voluntary since it varies from fan to fan, each fan decides by him/herself about the contribution to be small or large. No registration if the potential fan is not willing to fulfill this sponsorship. In fact, any commitment to this sponsorship guarantees certain priorities to the fan, such as priority rights to purchase tickets for additional (inter)national soccer matches with or without discount, program booklets free of charge, and so on. Notice that any fan is allowed to be registrated (in a central database run by the national soccer association) for a number of distinct soccer teams (not necessarily one team), while contributing the annual voluntary sponsorship once (at the beginning of the soccer season). Table 3 surveys the essential notions about soccer teams and fans.
In summary, the fan database of professional Dutch soccer teams may be modeled as the triple
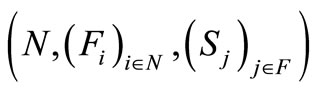 such that the “player set”
such that the “player set” 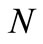 consists of the soccer teams, the set
consists of the soccer teams, the set  consists of fans of soccer team
consists of fans of soccer team 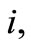 and
and  represents the annual voluntary sponsorship of fan
represents the annual voluntary sponsorship of fan 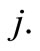 In fact, these sponsorships are combined to construct the following cost allocation
In fact, these sponsorships are combined to construct the following cost allocation 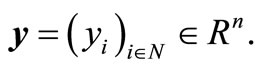 In the sequel let
In the sequel let 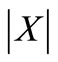 denote the cardinality of any finite set
denote the cardinality of any finite set  Consider the budget
Consider the budget 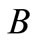 as the sum of sponsorships of fans with a unique (unspecified) favourite soccer team (that is,
as the sum of sponsorships of fans with a unique (unspecified) favourite soccer team (that is,  with
with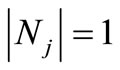 ). Firstly, factorize this budget in accordance with the appearance of the unique soccer team involved, that is
). Firstly, factorize this budget in accordance with the appearance of the unique soccer team involved, that is 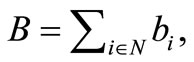 with the understanding that
with the understanding that 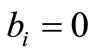 if there are no fans
if there are no fans 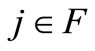 with unique favourite soccer team
with unique favourite soccer team 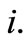 Secondly, with reference to these factorizations, determine the deviations with respect to their average. In summary, charge to soccer team
Secondly, with reference to these factorizations, determine the deviations with respect to their average. In summary, charge to soccer team 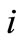 the cost allocation amounting
the cost allocation amounting 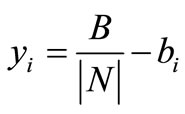 for all
for all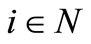 . In words, reward to soccer team
. In words, reward to soccer team 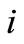 the negative amount
the negative amount , and charge the budget
, and charge the budget 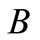 equally among all the soccer teams. In particular, a soccer team
equally among all the soccer teams. In particular, a soccer team 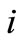 receives a reward (instead of a cost charge) if and only if the total sponsorship
receives a reward (instead of a cost charge) if and only if the total sponsorship ![]()
exceeds the average  of the budget. The larger
of the budget. The larger![]() the larger the reward to soccer team
the larger the reward to soccer team 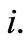 That is, soccer teams benefit from fans who are willing to contribute a large sponsorship. Table 4 surveys the essential notions in the setting of cost allocations.
That is, soccer teams benefit from fans who are willing to contribute a large sponsorship. Table 4 surveys the essential notions in the setting of cost allocations.
3. The Fan Data Cost Game
Our main goal is to support the cost allocation 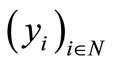 from the viewpoint of cooperative game theory as the so-called nucleolus [2] of the suitably chosen fan data cost game
from the viewpoint of cooperative game theory as the so-called nucleolus [2] of the suitably chosen fan data cost game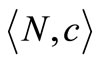 . Table 5 surveys the essential notions in the setting of fan data cost game.
. Table 5 surveys the essential notions in the setting of fan data cost game.
Definition 3.1. The coalitional cost  of any non-empty coalition
of any non-empty coalition 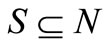 represents the loss (shortage) of coalitional sponsorship versus total sponsorship. That is, the fan data cost game
represents the loss (shortage) of coalitional sponsorship versus total sponsorship. That is, the fan data cost game 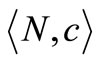 is given by
is given by
 (3.1)
(3.1)
Note that the soccer teams are willing to cooperate to share the fan data information of the central database in order to solve the minimization problem of shortages of sponsorships in that 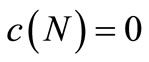 reflecting the formation
reflecting the formation

Table 2. The top seven of the last three final CPM rankings is as follows (R = ranking).

Table 3. The essential notions about soccer teams and fans.

Table 4. The essential notions in the setting of cost allocations.
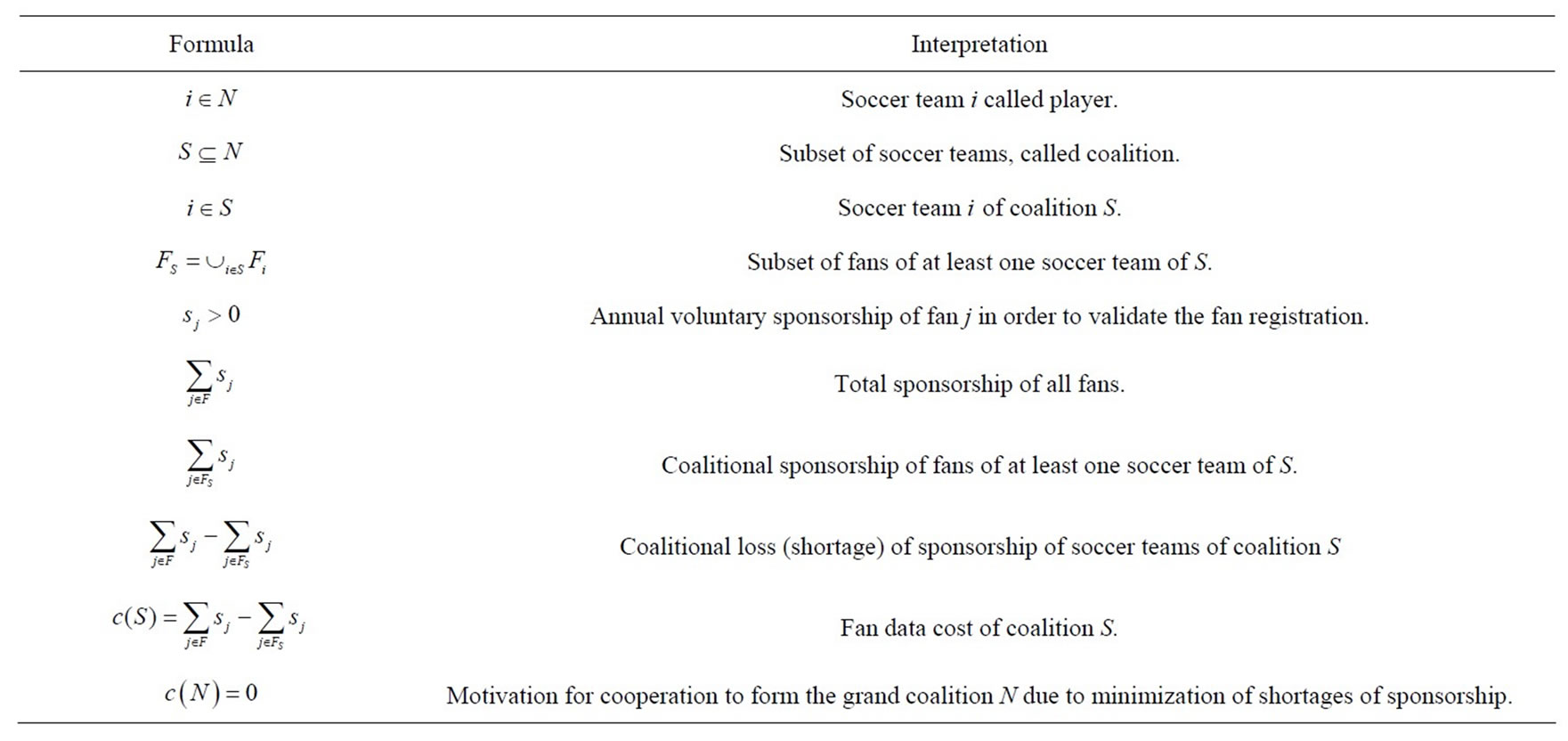
Table 5. The essential notions in the setting of fan data cost game.
of the grand coalition  The next preliminary Lemma reports two essential properties of the fan data cost game
The next preliminary Lemma reports two essential properties of the fan data cost game .
.
Lemma 3.2. Let 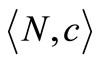 be the fan data cost game of (3.1).
be the fan data cost game of (3.1).
For all ,
,
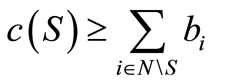 or equivalently, by (3.1)(3.2)
or equivalently, by (3.1)(3.2)
 (3.3)
(3.3)
 for all
for all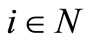 (3.4)
(3.4)
Proof. (3.3) follows immediately from the inclusion
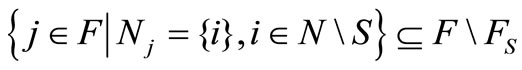 . In order to prove (3.4), fix player
. In order to prove (3.4), fix player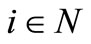 . By (3.1), we obtain the following chain of equations:
. By (3.1), we obtain the following chain of equations:
 .
.
Here the second equality is due to the following equivalences (given ):
):
 and
and 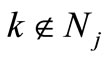 for all
for all 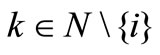
 and
and 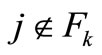 for all
for all 
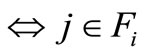 and
and 

4. The Nucleolus of the Fan Data Cost Game
Our study of the nucleolus involves the notion of excess
 , where
, where and
and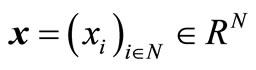 . It turns out that the level of the smallest excesses with respect to our cost allocation
. It turns out that the level of the smallest excesses with respect to our cost allocation 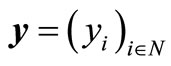 is composed of all the
is composed of all the  -person coalitions
-person coalitions  Indeed, on the one hand, by (3.4), and on the other, by (3.2), it holds for all
Indeed, on the one hand, by (3.4), and on the other, by (3.2), it holds for all  and all
and all .
.
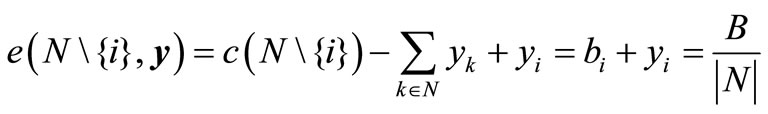
and further
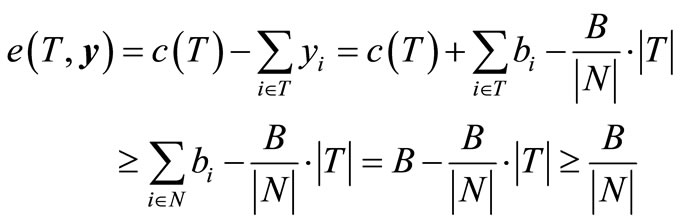
Hence, all 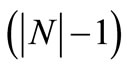 -person coalitions have the smallest excess among non-trivial coalitions with respect to our cost allocation y and according to Kohlberg’s criterion [3], this suffices to conclude that our cost allocation y agrees with the nucleolus of the fan data cost game
-person coalitions have the smallest excess among non-trivial coalitions with respect to our cost allocation y and according to Kohlberg’s criterion [3], this suffices to conclude that our cost allocation y agrees with the nucleolus of the fan data cost game  of the form (3.1). Thus, in the setting of fan data cost games, its nucleolus is fully solved by the explicit form of our cost allocation
of the form (3.1). Thus, in the setting of fan data cost games, its nucleolus is fully solved by the explicit form of our cost allocation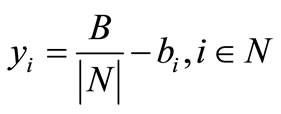 and so, numerical methods and computational complexity are replaced by theoretical results due to the significant property (3.2) of the fan data cost game. Clearly, the number of constraints in (3.2) is the same as the exponential number of non-trivial coalitions. According to the equivalent property (3.3), slight changes in the sponsorships do not affect the strict inequalities and so, stability applies to some extent.
and so, numerical methods and computational complexity are replaced by theoretical results due to the significant property (3.2) of the fan data cost game. Clearly, the number of constraints in (3.2) is the same as the exponential number of non-trivial coalitions. According to the equivalent property (3.3), slight changes in the sponsorships do not affect the strict inequalities and so, stability applies to some extent.
5. A Four-Person Example of a Fan Data Cost Game
Example 5.1. The four soccer teams of Ajax Amsterdam (A), Olympique Lyon (L), Real Madrid (M), and Dynamo Zagreb (Z) compete against each other within one group during the first round of the Champions League 2011-2012. Suppose that six television stations are appointed to broadcast the mutual matches such that the public Spanish TV station 3 is interested in all the four soccer teams, the public French TV station 2 is interested in every team except Zagreb, the national Dutch and Croatian TV stations 1 and 6 respectively only in their home team, similar to the local French and Spanish TV stations 4 and 5 respectively. That is, the data sets  of fans of these four soccer teams are given by
of fans of these four soccer teams are given by
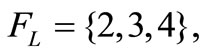
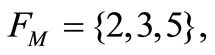
 Based on the existence of the TV stations
Based on the existence of the TV stations 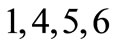 with a unique specified favourite soccer team
with a unique specified favourite soccer team , the sponsorships
, the sponsorships  by these four TV stations are allocated to the corresponding soccer teams as separable benefits
by these four TV stations are allocated to the corresponding soccer teams as separable benefits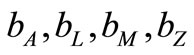 . In the second stage the total budget
. In the second stage the total budget 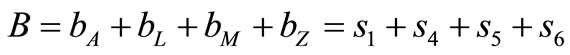 is divided equally among all the four soccer teams resulting in the allocations amounting
is divided equally among all the four soccer teams resulting in the allocations amounting


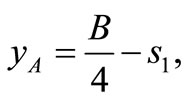 and
and 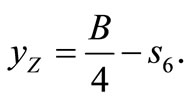
This final allocation is supported by the game theoretic approach as the solution concept called nucleolus of the fan data cost game 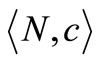 listed in Table 6. Notice that the fourth column concerning the cost of any coalition is equal to the fifth column concerning the sum of separable benefits of the soccer teams in the complementary coalition, except for coalition
listed in Table 6. Notice that the fourth column concerning the cost of any coalition is equal to the fifth column concerning the sum of separable benefits of the soccer teams in the complementary coalition, except for coalition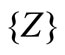 . The dominance of the fourth column to the fifth column is the most significant property (3.2) of the fan data cost game.
. The dominance of the fourth column to the fifth column is the most significant property (3.2) of the fan data cost game.
The core of the fan data cost game is a quadrilateral with extreme points 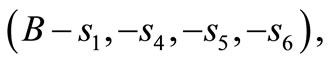
Table 6. The essential notions in the example.
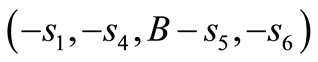
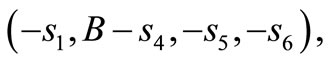 and
and
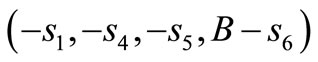 , where
, where 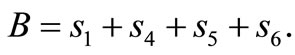 Without going into details, we report that the nucleolus of any fan data cost game coincides with the center of gravity of the core. In case a seventh TV station joins with only interest in the Dutch team Ajax, then the separable benefit of Ajax increases with the sponsorship s7 of the new TV station up to
Without going into details, we report that the nucleolus of any fan data cost game coincides with the center of gravity of the core. In case a seventh TV station joins with only interest in the Dutch team Ajax, then the separable benefit of Ajax increases with the sponsorship s7 of the new TV station up to 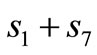 whereas the final cost charge to Ajax lowers by
whereas the final cost charge to Ajax lowers by , that is the cost charge to any of the other three soccer teams increases with
, that is the cost charge to any of the other three soccer teams increases with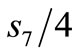 .
.
6. A Remark about the Core of the Sponsorship Game
In the setting of the division problem of the total budget 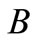 among the soccer teams, it is natural to study the sponsorship game
among the soccer teams, it is natural to study the sponsorship game 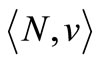 defined by
defined by
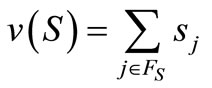 for all
for all 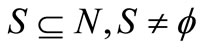 (6.1)
(6.1)
Clearly, straight from its definition, 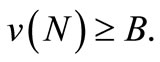 Unfortunately, this sponsorship game has the drawback that its so-called “core” is empty. For that purpose, consider the set of “reasonable” payoff vectors of the game consisting of efficient payoff vectors
Unfortunately, this sponsorship game has the drawback that its so-called “core” is empty. For that purpose, consider the set of “reasonable” payoff vectors of the game consisting of efficient payoff vectors 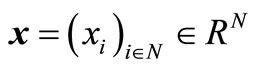 satisfying
satisfying  as well as lower and upper bounds for the individual payoffs such that
as well as lower and upper bounds for the individual payoffs such that 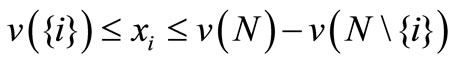 for all
for all 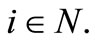 In the context of the sponsorship game
In the context of the sponsorship game 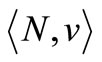 of the form (6.1), it holds for all
of the form (6.1), it holds for all 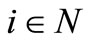
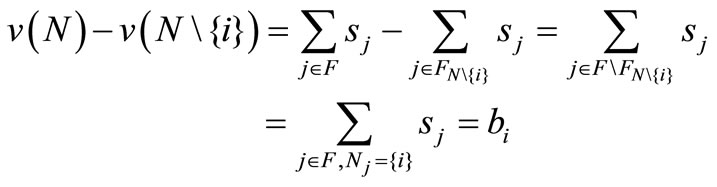
So any reasonable payoff vector ![]() satisfies
satisfies 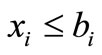 for all
for all 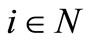 and consequently, by summing up,
and consequently, by summing up, 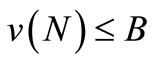 . This contradicts the earlier observation
. This contradicts the earlier observation 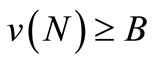 . So, reasonable payoff vectors do not exist, and hence, the core of the sponsorship game is empty too (as a subset).
. So, reasonable payoff vectors do not exist, and hence, the core of the sponsorship game is empty too (as a subset).
For an introductory book on cooperative game theory, we refer to [4]. For a paper with similar contents, we refer to [5].
7. Acknowledgements
The first author acknowledges financial support by National Science Foundation of China (NSFC) through grant No.71171163.
REFERENCES
- Van Duren and T. Knipping, “Het Ijzeren Gordijn Is Gesloopt,” Voetbal International (Weekly Soccer Magazine, in Dutch), Vol. 46, No. 13, 30 March 2011, pp. 116-121.
- D. Schmeidler, “The nucleolus of a characteristic function game,” SIAM Journal of Applied Mathematics, Vol. 17, No. 6, 1969, pp. 1163-1170. doi:10.1137/0117107
- E. Kohlberg, “On the nucleolus of a characteristic function Game,” SIAM Journal of Applied Mathematics, Vol. 20, No. 1, 1971, pp. 62-66.
- T. S. H. Driessen, “Cooperative Games, Solutions, and Applications,” Kluwer Academic Publishers, Dordrecht, 1988.
- P. Dehez and D. Tellone, “Data Games: Sharing public goods with exclusion,” Journal of Public Economic Theory, 2012.

