Journal of Biophysical Chemistry
Vol.2 No.3(2011), Article ID:6887,6 pages DOI:10.4236/jbpc.2011.23035
Vibrational spectra of oxygen and nitrogen-bridged iron octaethylporphyrin dimers by an U(2) algebraic technique
1Department of Electronics & Instrumentations, Lakireddy Bali Reddy College of Engineering, Mylavaram, India; *Corresponding Author: sinivasakarumuri@gmail.com
2Department of Mathematics, GITAM University, Hyderabad, India;
3Department of Chemistry, P. G. Centre, P. B. Siddhartha College, Vijayawada, India;
4Department of Chemistry, Krishna University, Machilipatnam, India;
5Department of Applied Mathematics, Andhra University, Vishakapatnam, India.
Received 14 February 2011; revised 13 April 2011; accepted 20 June 2011.
Keywords: Vibrational Spectra; Lie Algebra; Octatehylporphyrin
ABSTRACT
Using U(2) algebraic model Hamiltonian the resonance Raman spectra of Oxygen bridged iron porphyrin dimers (OEPFe)2O and (OEPFe)2N calculated for selected some vibrational modes. Using this model the Hamiltonian so constructed, we have calculated vibrational energy levels of (OEPFe)2O and (OEPFe)2N accuractly.
1. INTRODUCTION
The structural and electronic properties of a number of metalloporphyrins and heme proteins have been elucidated with resonance Raman (RR) spectroscopy [1,2]. Vibrational spectra of metalloporphyrins are necessary not only to assign resonance Raman lines of hemoproteins but also to study the excited electronic states of metalloporphyrins with the vibronic interactions. Last two decades, few group members have done experimental and theoretical work on metalloporphyrins [3,4]. Vibrational assignments of the resonance Raman spectra of various metalloporphyrins have been extensively studied by several groups [5-8]. Recently, an algebraic approach has been proposed for the study of bio-molecular spectroscopy [9-10]. In the algebraic approach, the vibrational Hamiltonian is expanded in terms of certain operators in Lie algebra; U(4) in the full three-dimensional approach and U(2) in the simpler one-dimensional approach [11-26].
In the present paper, we have calculated the in-plane fundamental and combinational vibrational frequencies of Oxygen-bridged iron porphyrin dimmers at various wavelengths using U(2) algebraic approach.
2. THEORY: U(2) ALGEBRAIC APPROACH
In constructing this model, we use the isomorphism of the Lie algebra of U(2) with that of the one-dimensional Morse oscillator [27]. The eigen states of the one-dimensional Schrodinger equation, hψ = Єψ, with a Morse potential [28]
 (1)
(1)
can be put into one to one correspondence with the representations of U(2) É O(2), characterized by the quantum numbers |N, mñ, with the provision that one takes only the positive branch of m, i.e. m = N, N – 2,  , 1 or 0 for N = odd or even (N = integer). The Morse Hamiltonian (1) corresponds in the U(2) basis to a simple Hamiltonian, h = Є0 + AC, where C is the invariant operator of O(2), with eigen values (m2 – N2).
, 1 or 0 for N = odd or even (N = integer). The Morse Hamiltonian (1) corresponds in the U(2) basis to a simple Hamiltonian, h = Є0 + AC, where C is the invariant operator of O(2), with eigen values (m2 – N2).
The eigen values of h are Є = Є0 + A (m2 – N2) (2)
M = N, N – 2,  , 1 or 0 (N = integer).
, 1 or 0 (N = integer).
Introducing the vibrational quantum number ν = (N – m)/2, Eq.2 can be rewritten as
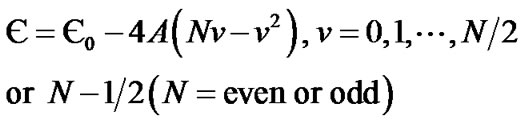 (3)
(3)
The values of Є0, A, and N are given in terms of μ, D, and α by Є0 = –D, –4AN = ћα (2D/μ)1/2, 4A = –ћ2α2/2μ. One can immediately verify that these are the eigen values of the Morse oscillator.
Now, consider a molecule with n bonds. In the algebraic model [29], each bond i is replaced by an algebra (here Ui(2)), with Hamiltonian hi = Є0i + AiCi, where Ci is the invariant operator of Oi(2) with eigen values –4(Niνi – The bonds interact with a bond-bond interaction. Two types of interaction are usually considered [29], which we denote by Cij and Mij, are called Casimir and Majorana interactions respectively.
The bonds interact with a bond-bond interaction. Two types of interaction are usually considered [29], which we denote by Cij and Mij, are called Casimir and Majorana interactions respectively.
The algebraic model Hamiltonian we consider is thus
 (4)
(4)
In Eq.4, Ci is an invariant operator with eigen values 4(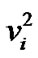 – Nivi) and the operator Cij is diagonal with matrix elements.
– Nivi) and the operator Cij is diagonal with matrix elements.
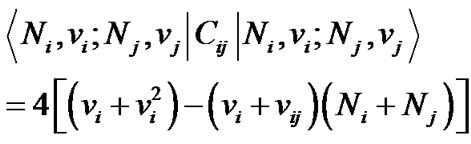 (5)
(5)
while the operator Mij has both diagonal and non-diagonal matrix element
 (6)
(6)
Eq.6 is a generalization of the two-bond model of Ref. [28] to n bonds.
2.1. Symmetry-Adapted Operators
In polyatomic molecules, the geometric point group symmetry of the molecule plays an important role. States must transform according to representations of the point symmetry group. In the absence of the Majorana operators Mij, states are degenerate. The introduction of the Majorana operators has two effects:
1) It splits the degeneracy’s of figure and (2) in addition it generates states with the appropriate transformation properties under the point group. In order to achieve this result the λij must be chosen in an appropriate way that reflects the geometric symmetry of the molecule. The total Majorana operator
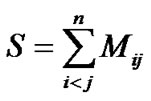 (11)
(11)
is divided into subsets reflecting the symmetry of the molecule
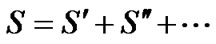 (12)
(12)
The operators S¢,  ,
,  are the symmetry-adapted operators. The construction of the symmetry-adapted operators of any molecule becomes clear in the following sections where the cases of Metalloporphyrins (D4h) discussed.
are the symmetry-adapted operators. The construction of the symmetry-adapted operators of any molecule becomes clear in the following sections where the cases of Metalloporphyrins (D4h) discussed.
2.2. Sample: Vibrational Analysis of Metalloporphyrins
As an example of the use of an algebraic method we analyze the stretching/bending vibrations of different Metalloporphyrins. We number the bonds as shown in Figure 1. Each bond, i, is characterized by its Vibron number Ni, and parameter Ai. The Casimir part of the interbond interactions is characterized by parameter Aij. For the Majorana part we can have, the view of symmetry of the molecule, two possible types of couplings:
Different Porphyrins are obtained by specific substitution at X or 1 to 8 positions.
By inspection of the Figure 1, one can see that two types of interactions in Metalloporphyrins:
1) First-neighbor couplings (Adjacent interactions);
2) Second-neighbor couplings (Opposite interactions).
The symmetry-adapted operators of Metalloporphyrins with symmetry D4h are those corresponding to these two couplings, that is,
 (13)
(13)

Figure 1. The structure of metalloporphyrins.
with
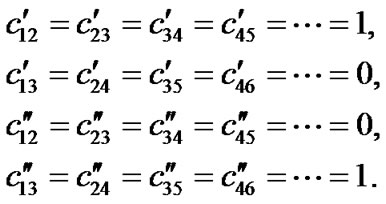
The total Majorana operator S is the sum
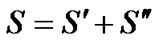 (14)
(14)
Diagonalization of S produces states that carry representations of S, the group of permutations of objects, while diagonalization of the other operators produces states that transform according to the representations A1g, A2g, B1g, B2g, E1u of D4h.
2.3. Local to Normal Transition: The Locality Parameter (()
The local-to-normal transition is governed by the dimensionless locality parameter (x). The local-to-normal transition can be studied [10] for polyatomic moleculesfor which the Hamiltonian is
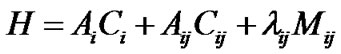 (18)
(18)
For these molecules, the locality parameters [9] are
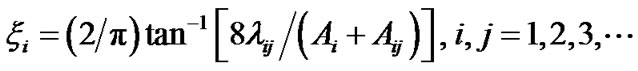 (19)
(19)
corresponding to the two bonds. A global locality parameter for XYZ molecules can be defined as the geometric mean
 (20)
(20)
Locality parameters of this metalloporphyrins are given in the results and discussions. With this definition, due to Child and Halonen [9,10], local-mode molecules are near to the x = 0 limit, normal mode molecules have x ® 1.
3. RESULTS & DESCUSSIONS
As an example, we report in the Table 1 & Table 2, the results of fundamental and combinational vibrational
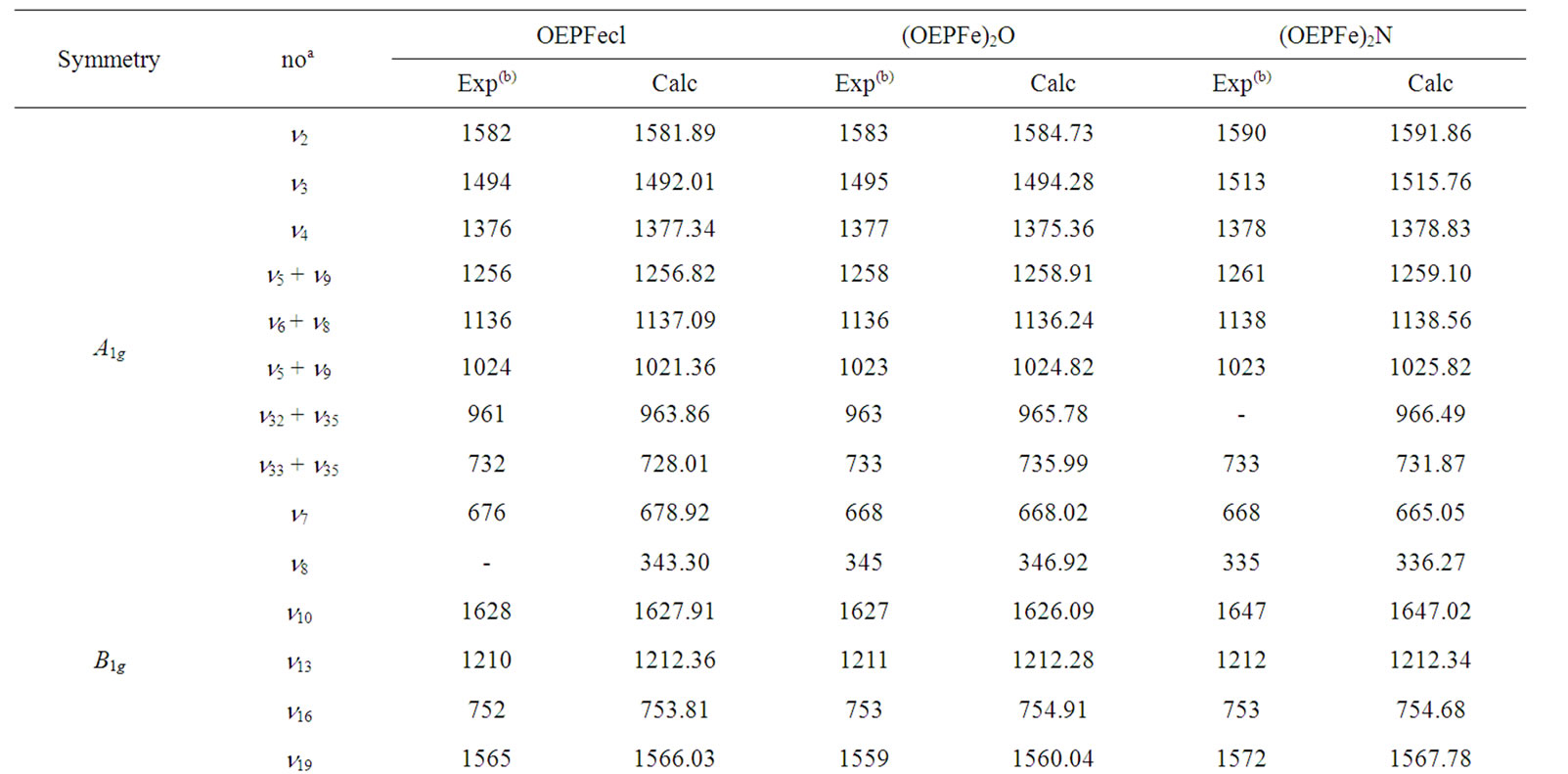

Table 1. Resonance Raman bands (cm–1) of OEPFecl, (OEPFe)2O and (OEPFe)2 N assignable to in-plane skeletal modes.
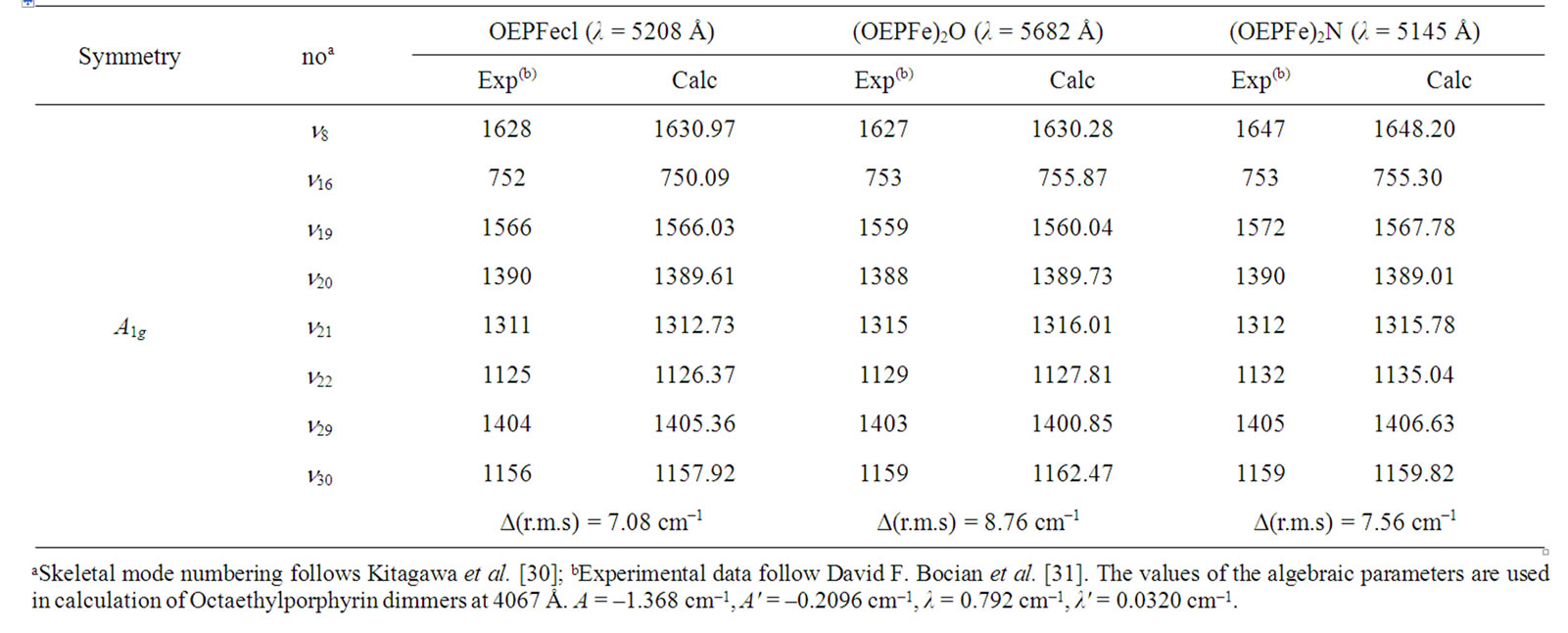
Table 2. Resonance Raman bands (cm–1) of (OEPFecl), (OEPFe)2O and (OEPFe)2N at λ = 5208 Å, λ = 5682 Å, and λ = 5145 Å respectively.
frequencies of OEPFecl, (OEPFe)2O and (OEPFe)2N at 4067 Å and at different wavelengths (λ = 5208 Å, λ = 5682 Å, and λ = 5145 Å) of Octaethyl dimers respectively. Here, we have used U(2) algebraic model to study the resonance Raman spectra of Octaethyl dimmers molecules with fewer algebraic parameters i.e. A, A', λ, λ' and N (Vibron number).
The values of vibron number can be determined [10] by the relation
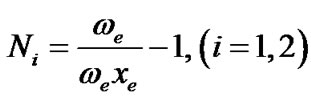
where ωe and ωexe are the spectroscopic constants of diatomic molecules of stretching and bending interactions of molecules considered. The Vibron number N between the diatomic molecules C-H & C-C are ≈44 and ≈140 respectively. This numerical value must be seen as initial guess; depending on the specific molecular structure, one can expect changes in such an estimate, which, however, should not be larger than ±20% of the original value (Eq.6). Using the established norms the Vibron numbers N and other algebraic parameters A, A', λ, λ' are determined.
From the view of group theory, the molecule of (OEPFecl), (OEPFe)2O & (OEPFe)2N takes a square planar structure with the D4h symmetry point group. Molecular vibrations of metalloporphyrins are classified into the in-plane and out of plane modes. For Octaethyl dimmers of D4h structure assuming the peripheral ethyl group is point mass the in-plane vibrations of Octaethyl dimmers are factorized into 35 gerade and 18 ungerade. Out of planes are factorized into 8 gerade and 18 ungerade modes. The A2u and Eu modes are IR active where the A1g, B1g, A2g, B2g & Eg modes are Raman active in an ordinary sense.
4. CONCLUSIONS
In the study of Resonance Raman spectra of Octaethyl dimers, we have applied one dimensional algebraic model i.e. U(2) Vibron model. In this study we reported RMS deviation and the locality parameter (x) for Oxygen and Nitrogen-Bridged Iron Octaethylporphyrin dimmers of in-plane skeletal modes at λ = 4067 Å and also for OEPFecl at λ = 5208 Å, (OEPFe)2O at λ = 5682 Å), and for (OEPFe)2N at λ = 5145 Å respectively.
In this study we reported the vibrations of Oxygen and Nitrogen-Bridged Iron Octaethylporphyrin dimmers are in accurate agreement with experimental data.
In this study the resonance Raman spectra of OEPFecl, (OEPFe)2O and (OEPFe)2N for in-plane skeletal modes at λ = 4067 Å (Table 1), we obtain the RMS deviation i.e. Δ(r.m.s) as 11.40 cm–1, 16.24 cm–1, 11.22 cm–1 and the locality parameters are x1 = 0.0231, x2 = 0.0234, x3 = 0.0232 respectively.
In this study the resonance Raman spectra of OEPFecl for in-plane skeletal modes at λ = 4067 Å (Table 2), we obtain the RMS deviation i.e. Δ (r.m.s) as 7.08 cm–1 and the locality parameter (x) = 0.0014.
In this study the resonance Raman spectra of (OEPFe)2O for in-plane skeletal modes at λ = 4067 Å (table 1), we obtain the RMS deviation i.e. Δ(r.m.s) as 8.76 cm–1 and the locality parameter (x) = 0.0019.
In this study the resonance Raman spectra of (OEPFe)2N for in-plane skeletal modes at λ = 4067 Å (Table 1), we obtain the RMS deviation i.e. Δ(r.m.s) as 7.56 cm–1 and the locality parameter (x) = 0.0017.
The locality parameter of Oxygen and Nitrogenbridged Iron Octatehylporphyrin dimmers at various wavelengths confirms that highly local mode behavior. Therefore, here the Hamiltonian mode is obviously the local Hamiltonian mode.
Hence, one may conclude that the algebraic local Hamiltonian mode fits well with the Oxygen and Nitrogen-bridged Iron Octatehylporphyrin dimmers at various wavelengths. Therefore the higher excited states and combinational bands are calculated using algebraic local Hamiltonian mode with sufficient experimental data.
5. ACKNOWLEDGEMENTS
The author Dr. Srinivasa Rao Karumuri would like to thank Prof. Thomson G. Spiro for providing necessary literature for this study.
The author Dr. Srinivasa Rao Karumuri also would like to thank The Department of Science & Technology, New Delhi, India, for providing the financial assistance for this study.
REFERENCES
- Spiro, T.G. (1982) Part II. In: Lever, A.B.P. and Gray, H.B., Eds., Iron Porphyrins, Addison-Wesley, Reading, 89-152.
- Felton, R.H. and Yu, N.-T. (1978) Vol. II. In: Dolphin, D., Ed., The Porphyrins, Academic Press, New York, 347- 388.
- Kitagawa, T., Ozaki, Y. and Kyogoku, Y. (1978) Resonance Raman studies on the ligand-iron interactions in hemoproteins and metallo-porphyrins. Advances in Biophysics, 11, 153.
- Tewari, S. and Das, R. (2004) A chakraborty and ramendu bhattacharjee, resonance Raman study on disorted symmetry of porphyrin in nickel metalloporphyrins. Pramana— Journal of Physics, 63, 1073.
- Kitagawa, T., Ogoshi, H., Watanabe, E. and Yoshida, Z. (1975) Resonance Raman scattering from metalloporphyrins. Metal and ligand dependence of the vibrational frequencies of octaethylporphyrins. The Journal of Physical Chemistry, 79, 2629-2635. doi:10.1021/j100591a012
- Abe, M., Kitagawa, T. and Kyogoku, Y. (1978) Resonance Raman evidence of chloride binding to the heme iron. The Journal of Physical Chemistry, 69, 4526. doi:10.1063/1.436450
- Spaulding, L.D., Chang, C.C., Yu, N.T. and Felton, R.H. (1975) Resonance Raman spectra of metallooctaethylporphyrins. Structural probe of metal displacement. Journal of the American Chemical Society, 97, 2517-2525.
- Spiro, T.G. and Li, X.Y. (1988) Vol. III. In: Spiro, T.G., Ed., Biological Applications of Raman Spectroscopy, Wiley, New York.
- Child, M.S. and Halonen, L.O. (1984) Overtone frequencies and intensities in the local mode picture. Advances in Chemical Physics, 54, 1-57. doi:10.1002/9780470142813.ch1
- Iachello, F. and Levine, R.D. (1995) Algebraic theory of molecules. Oxford University Press, Oxford.
- Van Roosmalen, O., Iachello, F., Levine, R.D. and Dieperink, A.E.L. (1983) The geometrical-classical limit of algebraic Hamiltonians for molecular vibrotational spectra. Journal of Chemical Physics, 79, 2515. doi:10.1063/1.446164
- Sarkar, N.K., Choudhury, J., Karumuri, S.R. and Bhattacharjee, R. (2008) An algebraic approach to the comparative study of the vibrational spectra of monofluoroacetylene (HCCF) and deuterated acetylene (HCCD). Molecular Physics, 106, 693. doi:10.1080/00268970801939019
- Sarkar, N.K., Choudhury, J. and Bhattacharjee, R. (2008) An algebraic approach: Study of vibrational spectra of some linear triatomic molecules. Indian Journal of Physics, 82, 767.
- Sarkar, N.K., Choudhury, J., Karumuri, S.R. and Bhattacharjee, R. (2009) A comparative study of vibrational spectra of OCS and HCP using Lie algebraic method. The European Physical Journal D, 53, 163. doi:10.1140/epjd/e2009-00094-8
- Choudhury, J., Karumuri, S.R., Sarkar, N.K. and Bhattacharjee, R. (2008) Vibrational spectroscopy of SnBr4 and CCl4 using Lie algebraic approach. Pramana— Journal of Physics, 71, 439. doi:10.1007/s12043-008-0123-z
- Choudhury, J., Sarkar, N.K. and Bhattacharjee, R. (2008) Algebraic approach to analyze the vibrational spectra of tetrahedral molecules. Indian Journal of Physics, 82, 561.
- Choudhury, J., Karumuri, S.R., Sarkar, N.K. and Bhattacharjee, R, (2009) Vibrational spectroscopy of CH/CD stretches in propadiene: An algebraic approach. Chinese Physics Letters, 26, 020308. doi:10.1088/0256-307X/26/2/020308
- Karumuri, S.R., Sarkar, N.K., Choudhury, J. and Bhattacharjee, R. (2009) Analysis of resonance Raman spectra of Nickel octaethylporphyrin using Lie algebra. Journal of Environmental Research and Development, 3, 250-256.
- Karumuri, S.R., Sarkar, N.K., Choudhury, J. and Bhattacharjee, R. (2009) Study of vibrational spectra of nickel metalloporphyrins: An algebraic approach. Pramana— Journal of Physics, 72, 517. doi:10.1007/s12043-009-0046-3
- Karumuri, S.R., Sarkar, N.K., Choudhury, J. and Bhattacharjee, R. (2008) Vibrational spectroscopy of Cm-H, Cb-Cb stretching vibrations of nickel metalloporphyrins: An algebraic approach. Molecular Physics, 106, 1733. doi:10.1080/00268970802248998
- Karumuri, S.R. Sarkar, N.K., Choudhury, J. and Bhattacharjee, R. (2009) U(2) algebraic model applied to stretching vinrational spectra of metalloporphyrins. Journal of Molecular Spectroscopy, 255, 183. doi:10.1016/j.jms.2009.03.014
- Karumuri, S.R., Sarkar, N.K., Choudhury, J. and Bhattacharjee, R. (2009) Vibrational spectroscopy of stretching and bending modes of nickel tetra phenyl porphyrins: An algebraic approach. Chinese Physics Letters, 26, 093301. doi:10.1088/0256-307X/26/9/093301
- Karumuri, S.R., Sarkar, N.K., Choudhury, J. and Bhattacharjee, R. (2010) Vibrational spectroscopy of Cm-C, Cb-Cb vibrations of copper tetramesityl porphryin. Pramana—Journal of Physics, 74, 57-66.
- Karumuri, S.R., Siva Rama Prasad, A., Sarkar, N.K., Choudhury, J. and Bhattacharjee, R. (2010) Overtone spectra of Porphyrins and its substituted forms: An algebraic approach. Journal of Biophysical Chemistry, 1, 119-133.
- Alhassid, Y., Gursey, F. and Iachello, F. (1983) Group theory approach to scattering. Annals of Physics, 148, 346. doi:10.1016/0003-4916(83)90244-0
- Alhassid, Y., Iachello F. and Gürsey, F. (1983) Group theory of the Morse oscillator. Chemical Physics Letters, 99, 27. doi:10.1016/0009-2614(83)80263-2
- Levine, R.D. (1983) Representatio of one dimensional motion in a morse potential by a quadratic hamiltonian. Chemical Physics Letters, 95, 87-90. doi:10.1016/0009-2614(83)85071-4
- Van Roosmalen, O.S., Benjamin, I. and Levine, R.D. (1984) A unified algebraic model description for interacting vibrational modes in ABA molecules. Journal of Chemical Physics, 81, 5986-5997. doi:10.1063/1.447600
- Iachello, F. and Levine, R.D. (1982) Algebraic approach to molecular rotation-vibration spectra. I. Diatomic molecules. Journal of Chemical Physics, 77, 3046. doi:10.1063/1.444228
- Kitagawa, T., Abe, M. and Ogoshi, H. (1978) Raman spectra of octaethylporphyrinato-Ni(II) and meso-deuterated and 15N substituted derivatives. I. Observation and assignments of non-fundamental Raman lines. Journal of Chemical Physics, 69, 4516. doi:10.1063/1.436441
- Hofmann, J.A. Jr. and Bocian, D.F. (1984) Resonance Raman spectra of oxygenand nitrogen-bridged iron octaethylporphyrin dimmers. Journal of Chemical Physics, 88, 1472-1479. doi:10.1021/j150652a006

