Applied Mathematics
Vol.4 No.4(2013), Article ID:30718,4 pages DOI:10.4236/am.2013.44095
Reliability Evaluation of Two-Stage Directed Semi-Markov Repairable Network Systems*
1Department of Mathematics & Physics, Shijiazhuang Tiedao University, Shijiazhuang, China
2Institute of Applied Mathematics, Hebei Academy of Sciences, Shijiazhuang, China
3Hebei Authentication Technology Engineering Research Center, Shijiazhuang, China
Email: fanruiqin@126.com, #wly-sjz@sohu.com, litongliang@tom.com
Copyright © 2013 Ruiqin Fan et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 11, 2013; revised February 11, 2013; accepted February 18, 2013
Keywords: Directed Network System; Reliability; Availability; Semi-Markov Repairable System; Markov Renewal Process
ABSTRACT
A two-stage directed Semi-Markov repairable network system is presented in this paper to model the performance of many transmission systems, such as power or oil transmission network, water or gas supply network, etc. The availability of the system is discussed by using Markov renewal theory, Laplace transform and probability analysis methods. A numerical example is given to illustrate the results obtained in the paper.
1. Introduction
A lot of transmission systems’ performance, such as power or oil transmission network, water or gas supply network etc. can be modeled by a directed network system. Those systems have a close relationship with people’s daily life and are crucial to guarantee the security of a community. The research on the reliability of these systems has been a hot topic [1,2]. Multi-state two-stage directed network systems are introduced in [3] and [4] to describe systems whose elements have more than two states. To overcome the “dimensional curse” problem and get the availability of these systems, a special technique which is based on the combination of the universal generating function (UGF) technique and random process methods is proposed [5-7]. Markov repairable systems are built in [8,9] to describe the evolution of these network systems with “smaller” state spaces. The availability and maintenance policy of them are studied. They assumed that the evolution of these systems can be determined by a Markov stochastic process. These assumptions mean that the sojourns in distinct states are all exponentially distribution and are independent each other. Hence these assumptions were unrealistic and restricted the application of the results. In the present paper, a two stage directed Semi-Markov system is introduced and it is a extension of the systems presented in [8].
The remainder of the paper is organized as follows. In Section 2, assumptions of two stage directed semiMarkov system are presented. The availability of the system is discussed is in Section 3. In Section IV a numerical example is given to illustrate results. Finally, a conclusion is given.
2. Model Description
2.1. Two-Stage Directed Network System
The details of the two-stage directed network system are as follow [8]. The media flows continuously from the supply system S to customers 1 and 2 passing through lines x1 and x2. Lines x1 and x2 may fail due to degradation. They will be repaired immediately while they fail. When line x1 works the fluid media can be transmitted to customer 1. When line x1 fails line x2 will be in cold spare state. When line x1 and line x2 work at the same time the fluid media will flow to customers and the system works, otherwise the system fail. Figure 1 shows the system.
According to the assumptions the system states can be defined as followsState 0: both of the two lines work;
State 1: line x1 works while line x2 fails and is maintaining;
State 2: line x1 fails and is maintaining and line x2 is in cold spare state;
State 3: line x2 fails and is maintaining, line 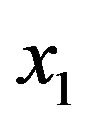 fails and is waiting for maintenance.
fails and is waiting for maintenance.
Hence the state space of the system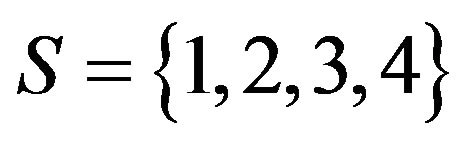 , the operating state set
, the operating state set 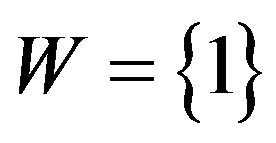 and the failed state set
and the failed state set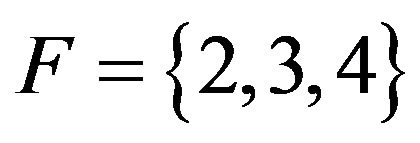 .
.
2.2. Semi-Markov Model for the Two-Stage Directed Network System
Assume that the evolution of the system can be described by a Markov renewal process with the Semi-Markov kernel 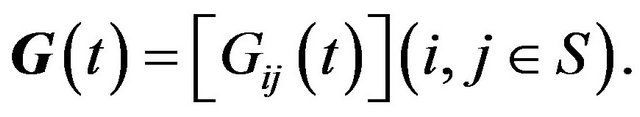 According to the assumptions of the system, the transition diagram of the system is as follows and shown in Figure 2.
According to the assumptions of the system, the transition diagram of the system is as follows and shown in Figure 2.
Let 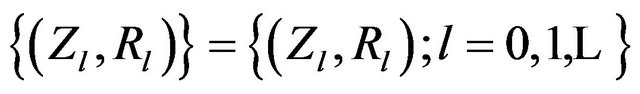 be the time homogeneous Markov renewal process which is the equivalent representation of
be the time homogeneous Markov renewal process which is the equivalent representation of 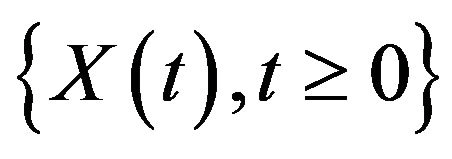 (see [10]). Then the process
(see [10]). Then the process 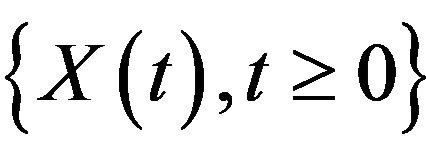 has transitions at epochs
has transitions at epochs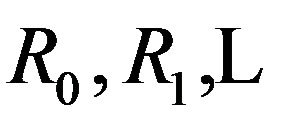 , and
, and 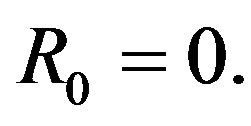 States are visited according to homogenous Markov chain
States are visited according to homogenous Markov chain  with transition probability matrix P. The increments
with transition probability matrix P. The increments  are the sojourn times at the individual states. They are distributed according to the arbitrary cumulative distribution function and, for each
are the sojourn times at the individual states. They are distributed according to the arbitrary cumulative distribution function and, for each , the distribution of
, the distribution of 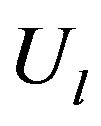 depends only on the state
depends only on the state 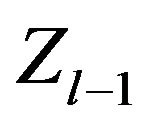 currently being visited and
currently being visited and  subsequently to be visited. Further more
subsequently to be visited. Further more
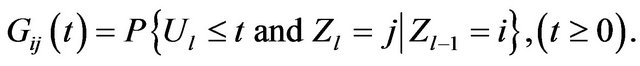
3. Reliability Evaluation of Multi-State Two-Staged Directed Network Systems
The instantaneous availability of the system, 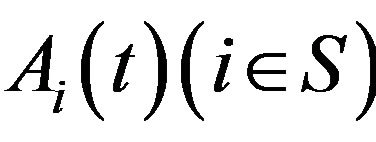 , is the probability that the system is functional given the
, is the probability that the system is functional given the
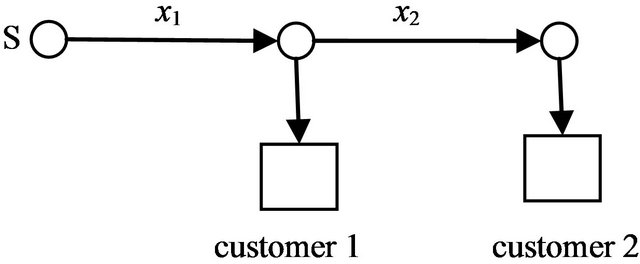
Figure 1. The two-stage directed network system.
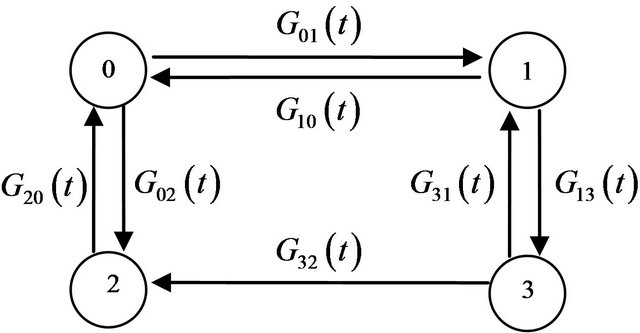
Figure 2. Semi-Markov model for the two-stage directed network system.
initial state i, that is
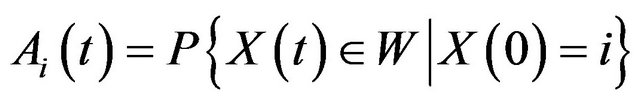 .
.
By classifying the states that the system is to be visited and the events that whether the process leaves the states i in  or not, we have, for
or not, we have, for 

Since, for any , the event
, the event  is impossible when
is impossible when , (1) reduces to
, (1) reduces to
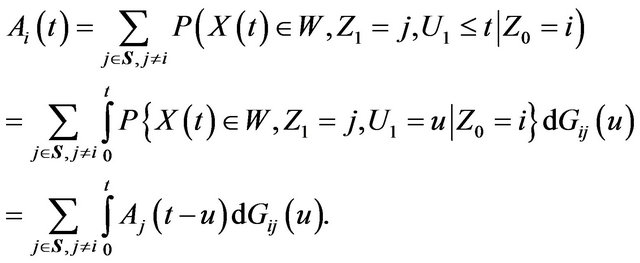
Similarly, for 
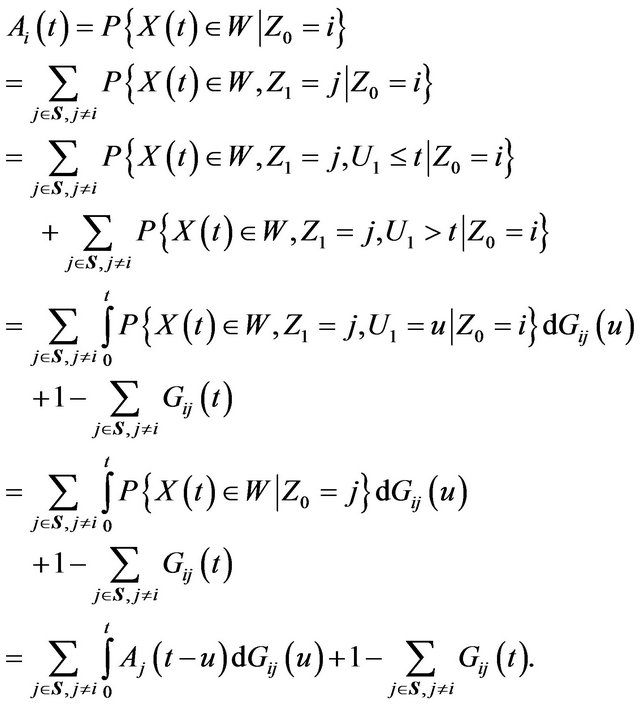
The second term of (3) corresponds the case that state transition does not occur before time t and the system is still functional at time t.
That is, we get a set of equations as follows on the instantaneous availability,
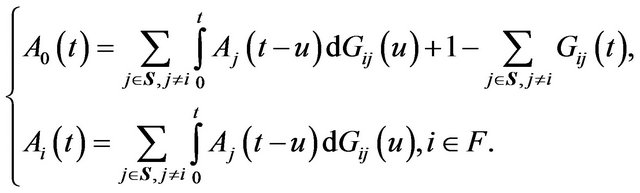
Taking the Laplace-Stieltjes transforms on both sides of the above set equations, we get
 (4)
(4)
where 
Solving the set of linear equations, we can get , then taking the inverse Laplace transformation, the instantaneous availability
, then taking the inverse Laplace transformation, the instantaneous availability  can be obtained.
can be obtained.
4. An Illustrative Example
Consider a heating transmitting system which can be described by a two-stage directed network system. The performance of the system is determined by a Markov renewal process. Assume that the transition functions of the Markov renewal process
 where
where 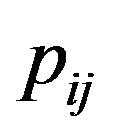 are elements of P, the transition probability matrix of Markov chain
are elements of P, the transition probability matrix of Markov chain 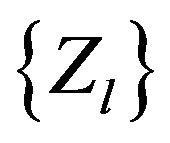 and
and

Figure 3. Curves of the instantaneous availability.
 .
.
Let 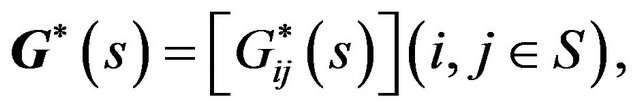 then
then

Using the results in Section III, we can get the instantaneous availability of the system  by Maple software. The formulae are so verbose that we don’t list them here and their curves are given in Figure 3. It is easy to see they are stabilized and the steady-state availability.
by Maple software. The formulae are so verbose that we don’t list them here and their curves are given in Figure 3. It is easy to see they are stabilized and the steady-state availability.
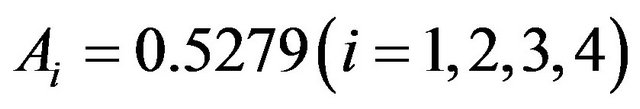 .
.
5. Conclusion
A two-stage directed Semi-Markov repairable Network system is introduced in this paper. The availability of the system is discussed by using Markov renewal theory, Laplace transform and probability analysis methods. The results given in this paper are useful for the risk evaluation of many transmission systems. The further research may include extension of the system to multi-stage situation and building more practical directed Network system model.
REFERENCES
- A. Lisnianski and G. Levitin, “Multi-State System Reliability, Assessment, Optimization and Application,” World Scientific Publishing Co. Pte. Ltd., Singapore City, 2003.
- K. S. Prabhata and K. S. Ashok, “Design of Water Supply Pipe Networks,” John Wiley & Sons, Inc., Hoboken, 2008.
- L. Wang, L. Cui and H. Sun, “Reliability Evaluation of Multi-State Two-Stage Directed Network Systems by Using Universal Generating Function,” Journal of Beijing Institute of Technology, Vol. 19, Suppl. 1, 2010, pp. 83- 85.
- H. Sun and L. Wang, “Reliability Evaluation of MultiState Two-Stage Directed Network Systems by Using Combined Stochastic Process Methods and Universal Generating Function,” 2nd International Workshop on Datebase Technology and Applications, Wuhan, 27-28 November 2010, pp. 411-414.
- I. Ushakov, “Universal Generating Function,” Soviet Journal of Computer and Systems Sciences, Vol. 24, No. 5, 1986, pp. 118-129.
- G. Levitin, “Universal Generating Function and Its Applications,” Springer, Berlin, 2005.
- A. Lisnianski and Y. Ding, “Redundancy Analysis for Repairable Multi-State System by Using Combined Stochastic Process Methods and Universal Generating Function Technique,” Reliability Engineering and System Safety, Vol. 94, No. 11, 2009, pp. 1788-1795. doi:10.1016/j.ress.2009.05.006
- M. Yu and L. Cui, “Modeling and Analysis for TwoStage Directed Network Markov Repairable Systems,” Transactions of Beijing Institute of Technology, Vol. 31, No. 6, 2011, pp. 753-756.
- M. Yu and L. Cui, “A Study on Optimal Availability for A Two-Stage Directed Network of Markov Repairable Systems,” The 4th Asia-Pacific International Symposium on Advanced Reliability and Maintenance Modeling, Wellington, 2010, pp. 796-803.
- E. Cinlar, “Markov Renewal Theory: A Survey,” Management Science, Vol. 21, No. 7, 1975, pp. 727-752. doi:10.1287/mnsc.21.7.727
NOTES
*Supported by the Science and Technology Key Project of Hebei Academic of Sciences (No. 12614,13607) & Hebei Province 333 HighLevel Personnel Training Project.
#Corresponding author.

