Advances in Pure Mathematics
Vol.3 No.1(2013), Article ID:27370,7 pages DOI:10.4236/apm.2013.31014
A Generalization of the Cayley-Hamilton Theorem
Department of Mathematics and Statistics, Himachal Pradesh University, Shimla, India
Email: rjkmrkanwar@yahoo.co.in
Received June 21, 2012; revised August 26, 2012; accepted September 11, 2012
Keywords: Polynomial Matrix; Square Matrix; Non-Singular Matrix; Adjoint of a Matrix; Leading Coefficient Matrix
ABSTRACT
It is proposed to generalize the concept of the famous classical Cayley-Hamilton theorem for square matrices wherein for any square matrix A, the det  is replaced by det
is replaced by det  for arbitrary polynomial matrix
for arbitrary polynomial matrix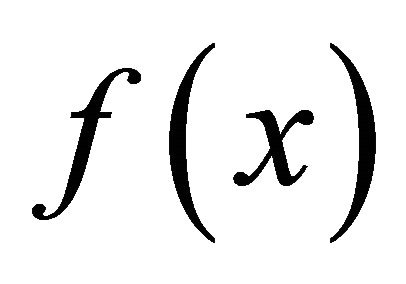 .
.
1. Introduction
The classical Cayley-Hamilton theorem [1-4] says that every square matrix satisfies its own characteristic equation. The Cayley-Hamilton theorem has been extended to rectangular matrices [5,6], block matrices [7,8], pairs of commuting matrices [9-11] and standard and singular two-dimensional linear systems [5,12]. The CayleyHamilton theorem has been extended to n-dimensional systems [13]. An extension of the Cayley-Hamilton theorem for 2D continuous discrete-time linear systems has been given in [14].
The Cayley-Hamilton theorem and its generalizations have been used in control systems [14,15] and also automation and control in [16,17], electronics and circuit theory [6], time-systems with delays [18-20], singular 2-D linear systems [5], 2-D continuous discrete linear systems [12], automation and electrotechnics [21], etc.
In this paper an overview of generalization of the Cayley-Hamilton theorem is presented. The linear polynomial matrix  of det
of det 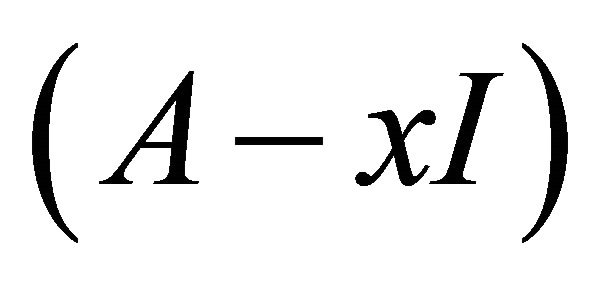 in the classical Cayley-Hamilton theorem is replaced by the general polynomial matrix
in the classical Cayley-Hamilton theorem is replaced by the general polynomial matrix

where 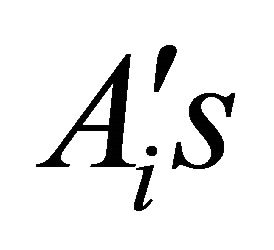 for
for  are square matrices of the same order. In the Theorem 1 given below it is proved that if
are square matrices of the same order. In the Theorem 1 given below it is proved that if 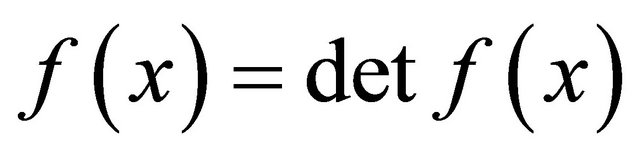 and whenever for a square matrix A
and whenever for a square matrix A 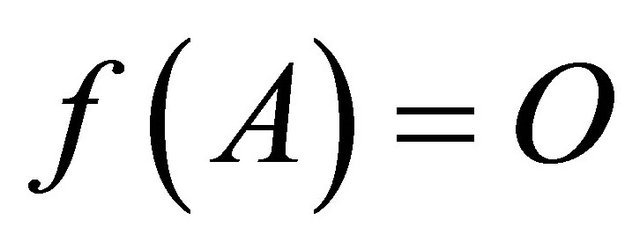 implies
implies  also. The converse of Theorem 1 is not true, is illustrated with the help of examples 1 and 2 in which the leading coefficient matrix of the polynomial matrix
also. The converse of Theorem 1 is not true, is illustrated with the help of examples 1 and 2 in which the leading coefficient matrix of the polynomial matrix  may be singular or non-singular. A relation between the coefficients of the polynomial
may be singular or non-singular. A relation between the coefficients of the polynomial 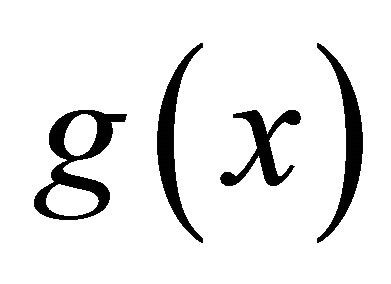 and the coefficient matrices of
and the coefficient matrices of 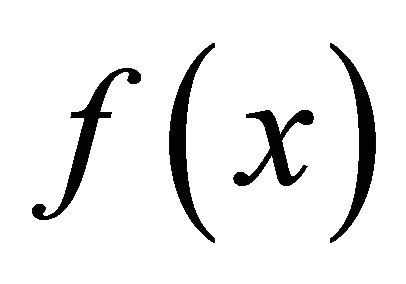 is worked out in corollaries 1, 2 and 3.
is worked out in corollaries 1, 2 and 3.
2. Preliminaries
Lemma 1. If the elements of a matrix A are polynomials in x of degree ≤ n, then A can be expressed as a polynomial matrix 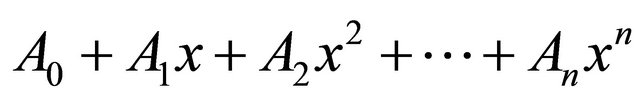 in x of degree ≤ n, where the matrices
in x of degree ≤ n, where the matrices  are of the same order as that of the matrix A.
are of the same order as that of the matrix A.
Illustration 1. Let

be a matrix of order 3 × 3. Then
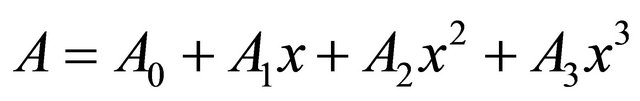 where
where
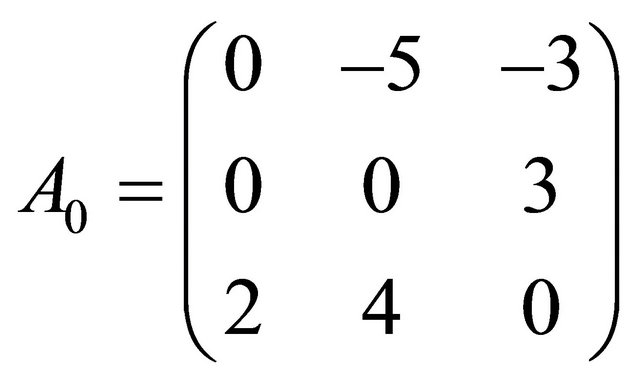 ;
; ;
;
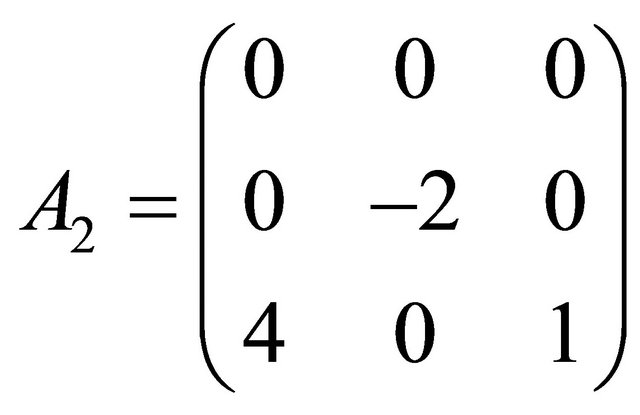 and
and 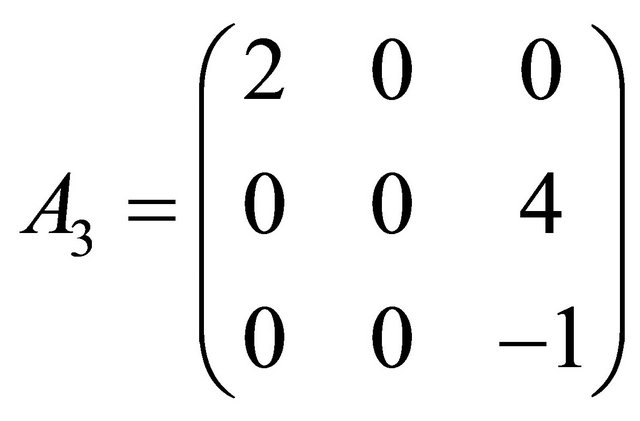
Lemma 2. If A is a square matrix of order n having elements as polynomials in x each of degree ≤ m, then the elements of the adjoint of the matrix A are also polynomials in x of degree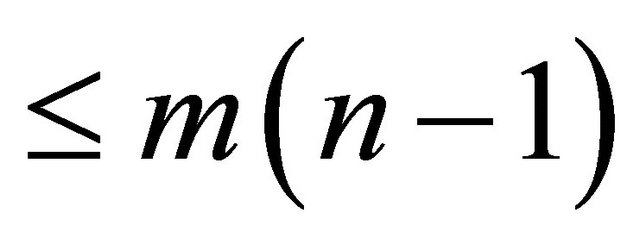 .
.
Illustration 2. Let

be a matrix of order 3 × 3 having elements as polynomials in x of degree ≤ 4, then
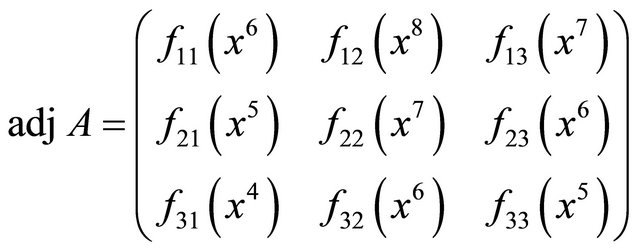 where
where 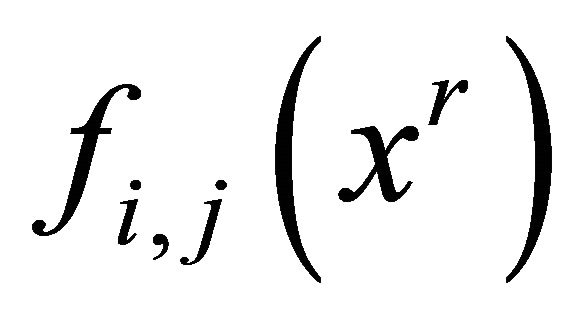 denotes the
denotes the 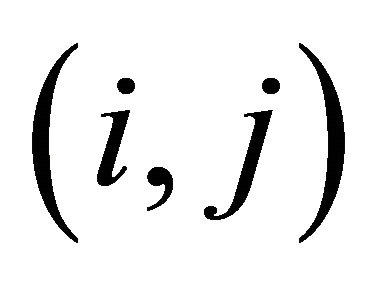 th element of the adjA, a polynomial in x of degree ≤ r. For instance in adjA, the element at the (2.1) th position is
th element of the adjA, a polynomial in x of degree ≤ r. For instance in adjA, the element at the (2.1) th position is
 .
.
Hence by the Lemma 1, because adjA contains elements as polynomials in x of degree ≤ 8, it implies that 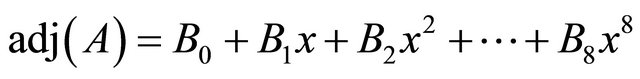 , where each of the
, where each of the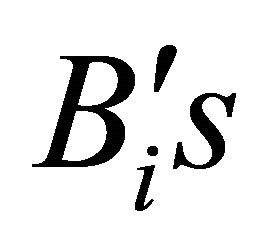 ,
, 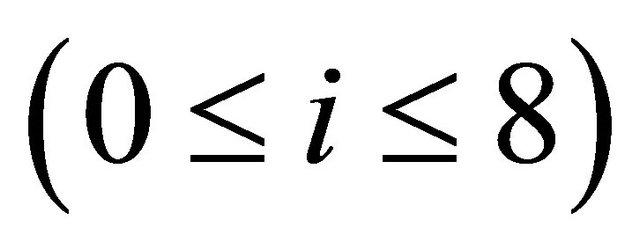 is also a square matrix of order 3.
is also a square matrix of order 3.
Remark 1. Prior to understand the concept in the proof of the main Theorem 1 given below, we first consider the following two illustrations of polynomial matrix  having the leading coefficient matrix singular or non-singular such that if
having the leading coefficient matrix singular or non-singular such that if  and for a square matrix A, whenever
and for a square matrix A, whenever
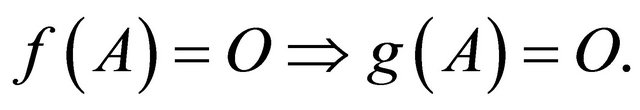
Illustration 3: Let
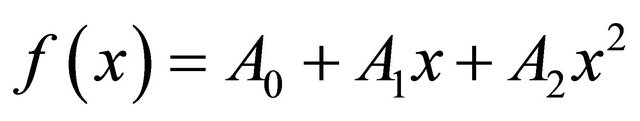 (2.1)
(2.1)
be a polynomial matrix over 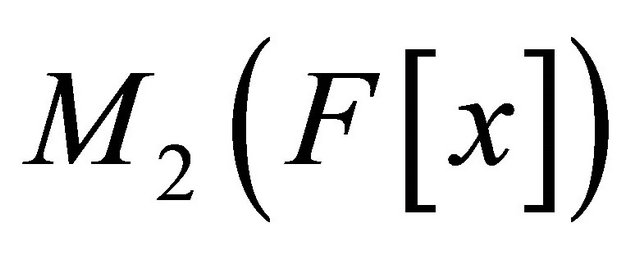 for
for
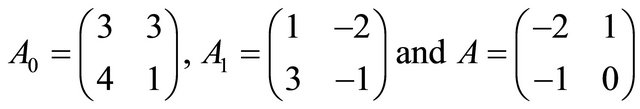 where A2 is a non-singular matrix and
where A2 is a non-singular matrix and  denotes the set of all 2 × 2 matrices whose elements are polynomials in x over the field F. Then there exists a matrix
denotes the set of all 2 × 2 matrices whose elements are polynomials in x over the field F. Then there exists a matrix  such that;
such that;
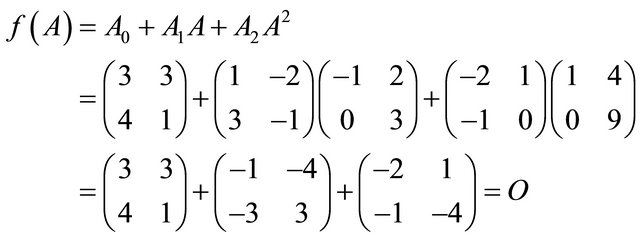
Also from (2.1), we have

Hence, 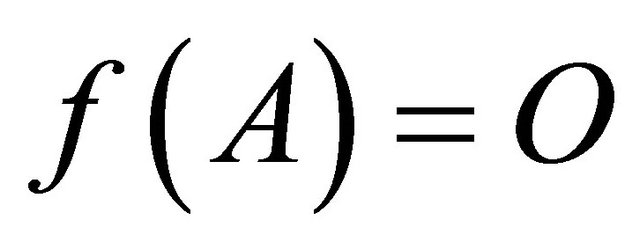 implies
implies 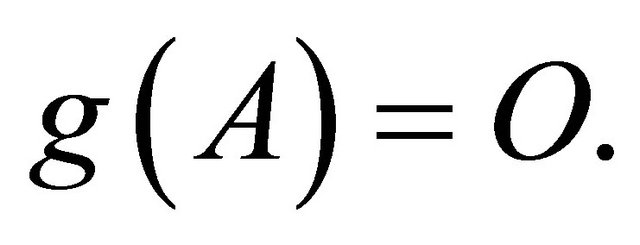
Illustration 4: Consider the polynomial matrix
 (2.2)
(2.2)
over , for
, for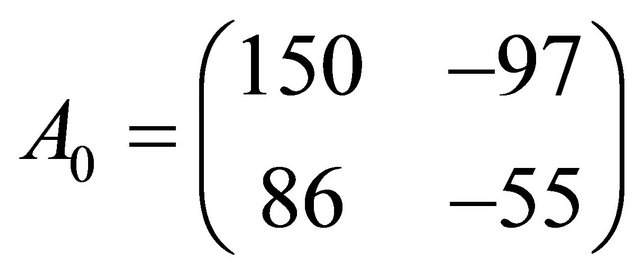 ;
;  and
and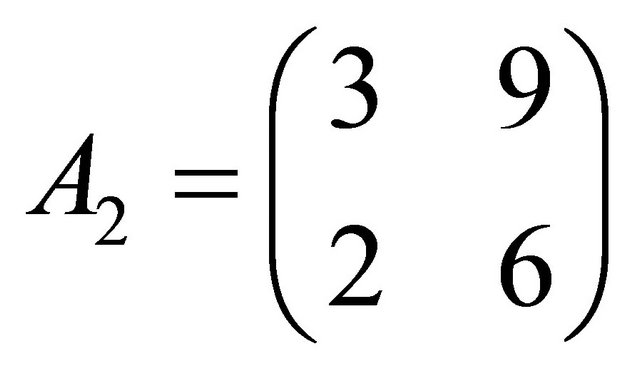 , where the leading coefficient matrix A2 is singular. Then there exists a matrix
, where the leading coefficient matrix A2 is singular. Then there exists a matrix  such that
such that
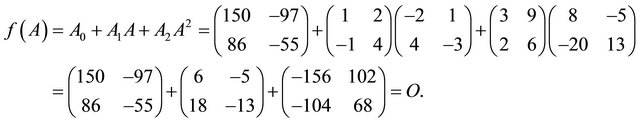
From (2.2), we have

As in Illustration 3, it can be easily verified that
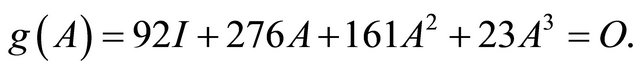
3. Main Results
Theorem 1. Let  be a polynomial matrix for
be a polynomial matrix for 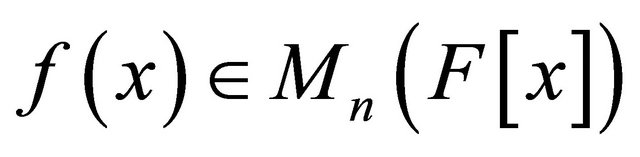 where
where 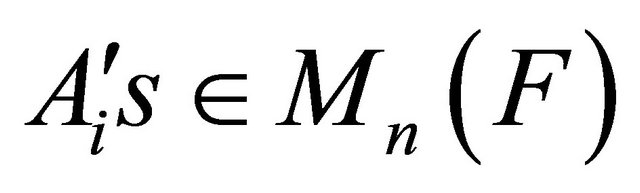 for
for , are square matrices of order n over the field F. If
, are square matrices of order n over the field F. If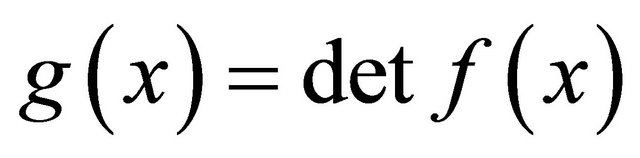 , then whenever
, then whenever  (Zero matrix) implies
(Zero matrix) implies 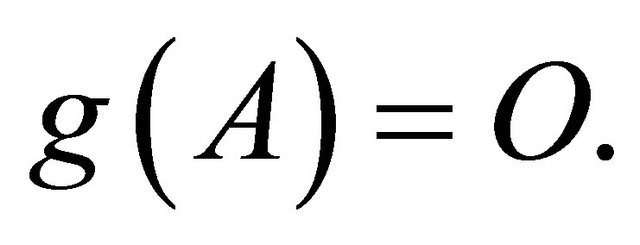 Converse is not true.
Converse is not true.
Proof. Since
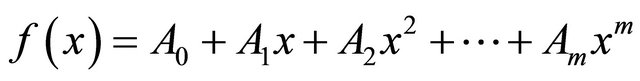 (3.1)
(3.1)
is itself is a matrix of order n × n having elements as polynomials in x each of degree ≤ m, therefore, using lemma 2, we have
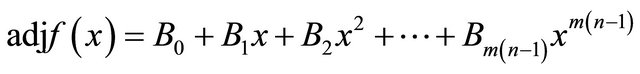 (3.2)
(3.2)
Also 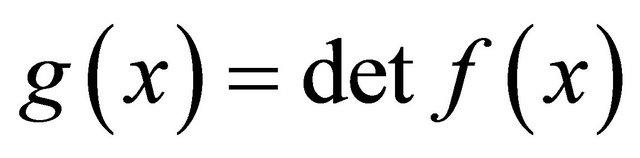 is a polynomial in x over
is a polynomial in x over 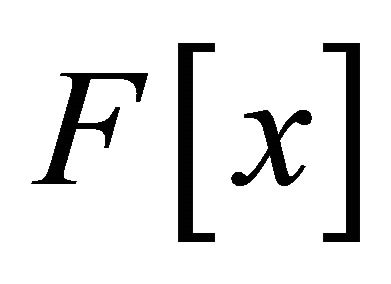 of degree ≤ mn. Therefore, using Lemma 1, we have
of degree ≤ mn. Therefore, using Lemma 1, we have
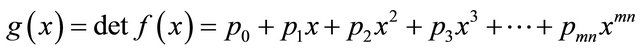 (3.3)
(3.3)
Since for any square matrix A, we have;
 (3.4)
(3.4)
where I is the identity matrix of the same order as of A. Now using (3.4), we have
 (3.5)
(3.5)
Therefore, using (3.1) to (3.3) above, we have from (3.5)
 (3.6)
(3.6)
Comparing coefficients of the corresponding terms on both sides of Equation (3.6), we get
 . (3.7)
. (3.7)
Multiplying the equations in (3.7) by the matrices
respectively and adding, we obtain;

Converse is not true. For this consider the following examples with the coefficient matrix singular and nonsingular respectively.
Example 1. Consider the function ; where
; where

Then for the scalar matrix , we have
, we have
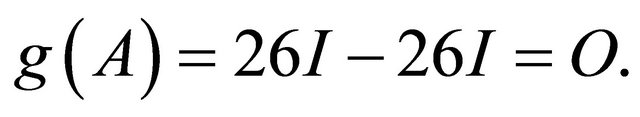 Whereas,
Whereas,
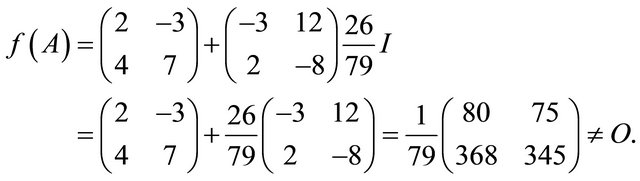
Example 2: Consider the function  ; where
; where
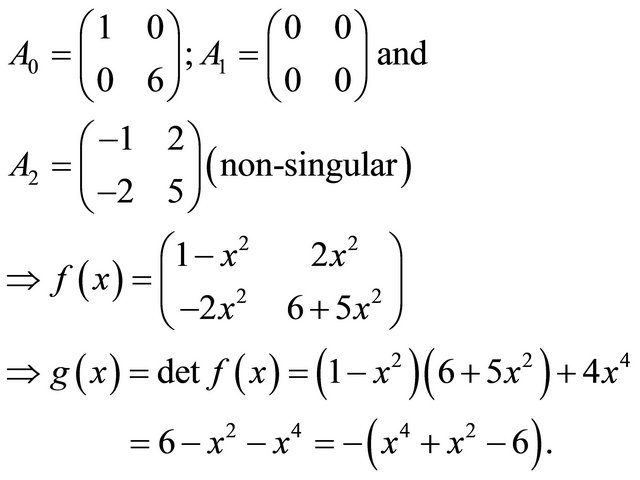
Then there exist infinite number of matrices A over the complex numbers C of the form
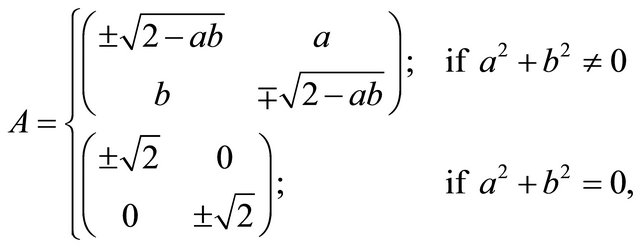
or

for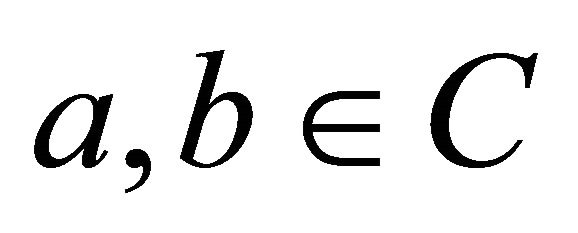 , such that
, such that 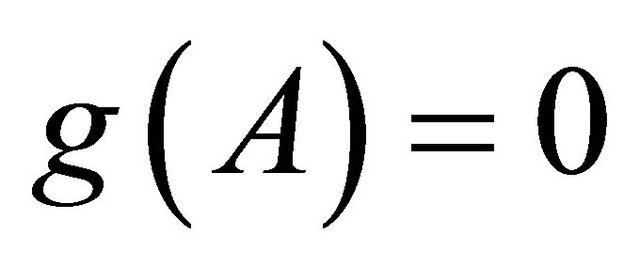 but
but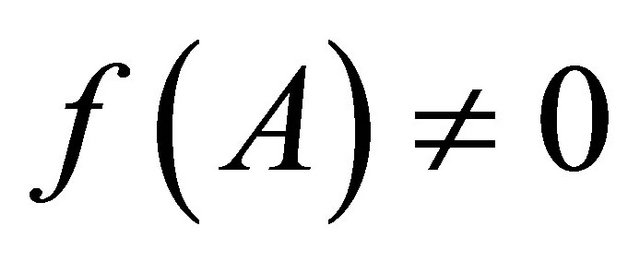 .
.
For instance, if ,
,  , then
, then

Whereas,
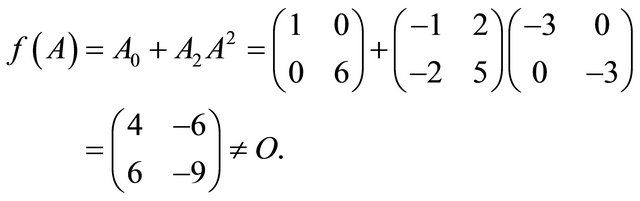
Illustration 5. For 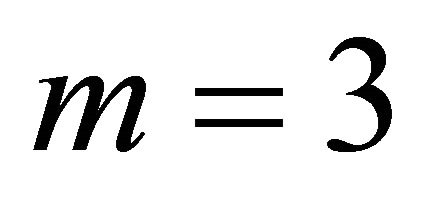 in Theorem 1, let
in Theorem 1, let

be a polynomial matrix in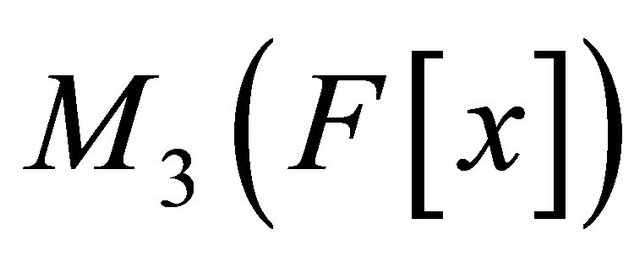 ,where
,where  such that
such that 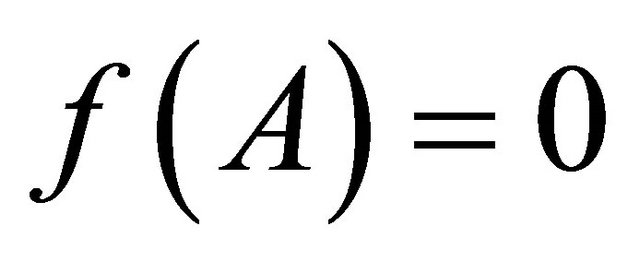 for some square matrix A of order 3.
for some square matrix A of order 3.
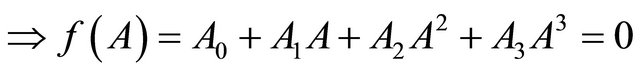 . (3.8)
. (3.8)
Since the elements of the matrix  are polynomials in x of degree
are polynomials in x of degree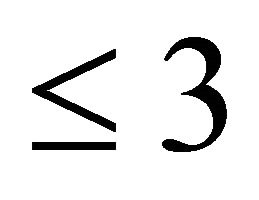
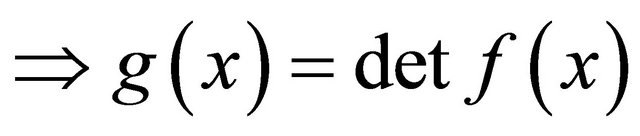
is a polynomial in x over the field F of degree ≤ 9. Therefore, let
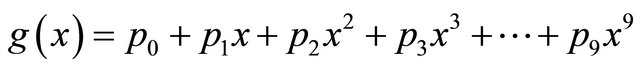 (3.9)
(3.9)
Also each element of the  being a polynomial in x of deg ≤ 6. So by Lemma (2), let
being a polynomial in x of deg ≤ 6. So by Lemma (2), let
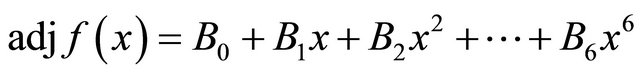 (3.10)
(3.10)
Now using (3.4), we have
 (3.11)
(3.11)
Comparing the coefficients of the equivalent powers of x on both sides, we have
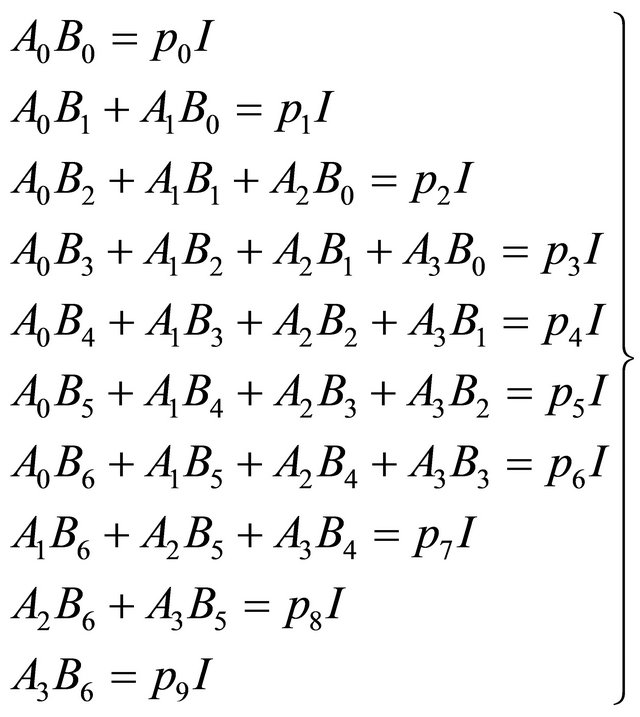 (3.12)
(3.12)
Multiplying these equations by  respectively and adding, we get;
respectively and adding, we get;
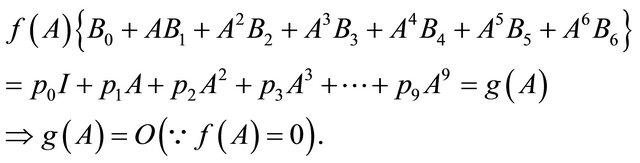
Corollary 1. If 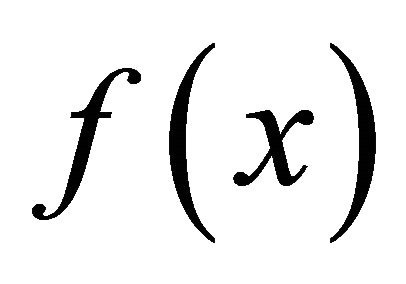 and
and  be the polynomials given in (3.1) and (3.3) respectively, then for
be the polynomials given in (3.1) and (3.3) respectively, then for
 .
.
Therefore, the constant term 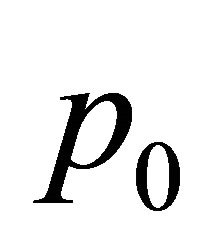 of the polynomial
of the polynomial  is the determinant of the constant term
is the determinant of the constant term 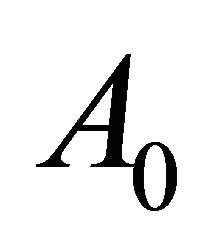 in the polynomial matrix
in the polynomial matrix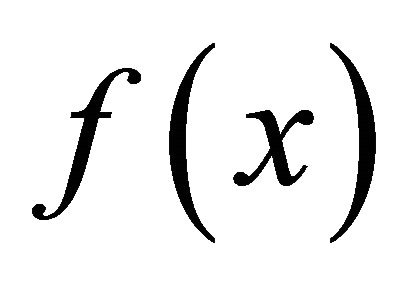 .
.
Corollary 2. From (3.1) and (3.3), for  , we have
, we have
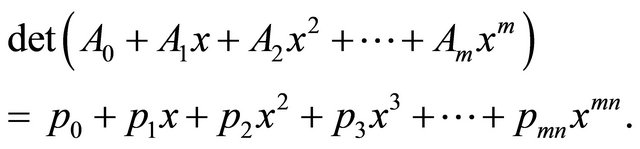 (3.13)
(3.13)
Therefore, in case for , when
, when  or
or , then from (3.13), we have
, then from (3.13), we have
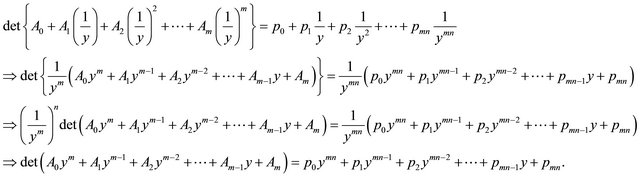 (3.14)
(3.14)
Therefore, if , then from (3.14), we get
, then from (3.14), we get 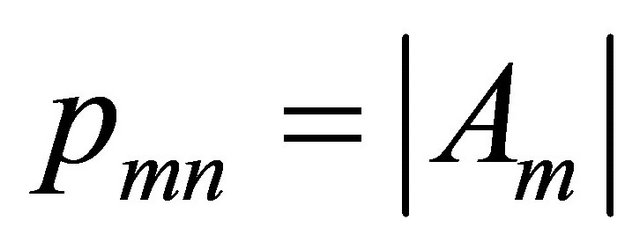 . Hence if,
. Hence if, .
.
Thus 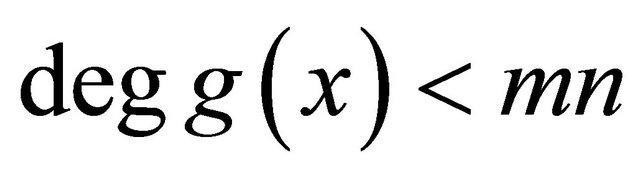 if the leading coefficient matrix
if the leading coefficient matrix  in
in 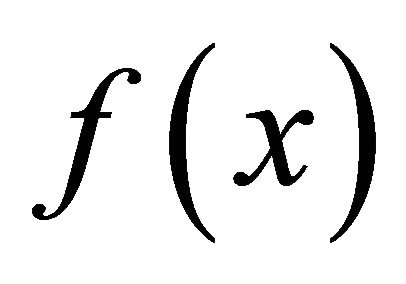 is singular.
is singular.
Corollary 3. If

be a bi-quadratic polynomial matrix for
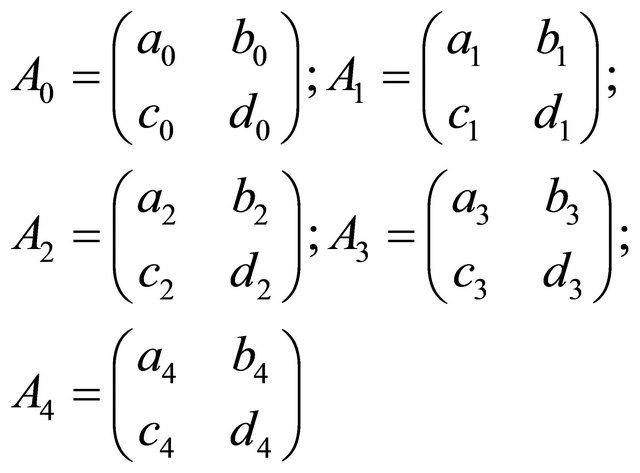
and if
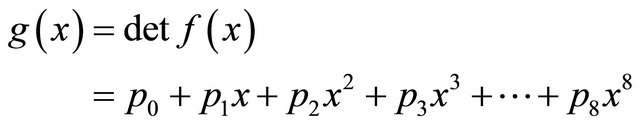
Then we have,

and so on.
In general, for any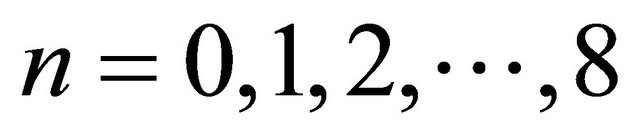 ; we have pn = coefficient of
; we have pn = coefficient of , for
, for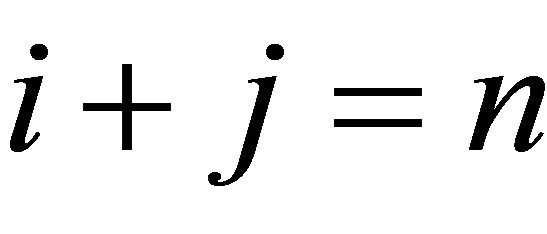 ;
;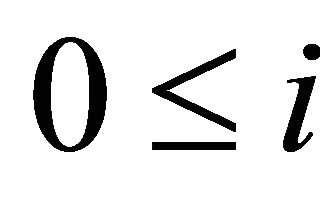 ,
, .
.
Example 3. Consider the cubic polynomial matrix
 where for
where for ,
,  , if we have
, if we have

where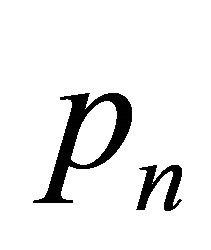 , the coefficient of
, the coefficient of  is given by
is given by
 (3.15)
(3.15)
It can be easily verified that
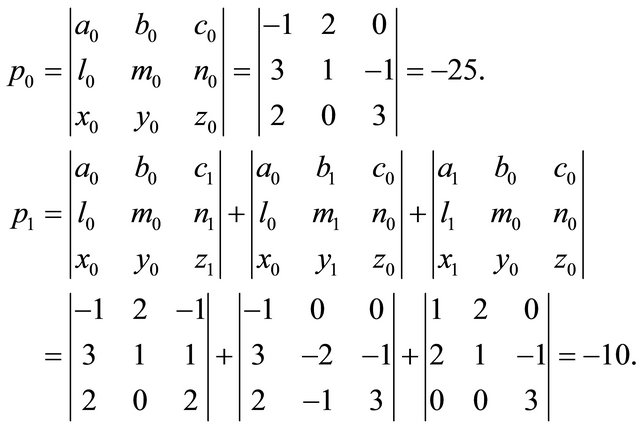
and

Similarly coefficients of the other powers of x, i.e., 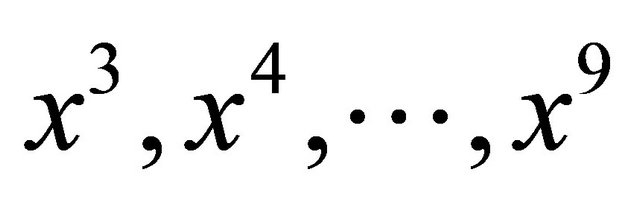 can be found by using (3.15). For instance
can be found by using (3.15). For instance
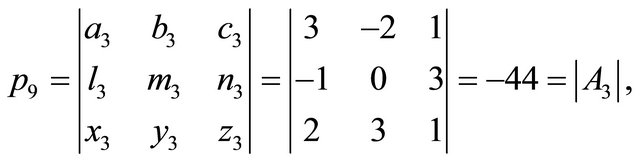
which verifies our assertion.
4. Conclusion
The concept of the Theorem 1 given above and the relation in (3.15) can be generalized to any polynomial matrix of arbitrary degree with coefficients as square matrices of any order.
5. Acknowledgements
The author wishes to thank Dr. P. L. Sharma, Associate Professor Department of Mathematics and Statistics of the H. P. University Shimla (H.P.) India for his help and guidance. He also expresses his gratitude to the Govt. of Himachal Pradesh Department of Higher Education for granting him study leave to complete the assigned project.
REFERENCES
- J. Gilbert and L. Gilbert, “Linear Algebra and Matrix Theory,” Academic Press Inc., New York, 1995.
- K. Hoffman and R. Kunze, “Linear Algebra,” Prentice Hall of India, New Delhi, 2010.
- P. Lancaster, “Theory of Matrices,” Academic Press, New York, 1969.
- F. R. Gantmatcher, “Theory of Matrices, Vol. 2,” Chelsea Publishing, New York, 1974.
- T. Kaczorek, “An Existence of the Cayley-Hamilton Theorem for Singular 2-D Linear Systems with Non-Square Matrices,” Bulletin of the Polish Academy of Sciences. Technical Sciences, Vol. 43, No. 1, 1995, pp. 39-48.
- T. Kaczorek, “Generalization of the Cayley-Hamilton Theorem for Non-Square Matrices,” International Conference of Fundamentals of Electronics and Circuit Theory XVIIISPETO, Gliwice, 1995, pp. 77-83.
- T. Kaczorek, “An Existence of the Caley-Hamilton Theorem for Non-Square Block Matrices,” Bulletin of the Polish Academy of Sciences. Technical Sciences, Vol. 43, No. 1, 1995, pp. 49-56.
- T. Kaczorek, “An Extension of the Cayley-Hamilton Theorem for a Standard Pair of Block Matrices,” Applied Mathematics and Computation Sciences, Vol. 8, No. 3, 1998, pp. 511-516.
- F. R. Chang and C. N. Chan, “The Generalized CayleyHamilton Theorem for Standard Pencils,” Systems & Control Letters, Vol. 18, No. 3, 1992, pp. 179-182. doi:10.1016/0167-6911(92)90003-B
- F. L. Lewis, “Cayley-Hamilton Theorem and Fadeev’s Method for the Matrix Pencil [sE-A],” 22nd IEEE Conference on Decision and Control, San Diego, 1982, pp. 1282-1288.
- F. L. Lewis, “Further Remarks on the Cayley-Hamilton Theorem and Fadeev’s Method for the Matrix Pencil [sEA],” IEEE Transactions on Automatic Control, Vol. 31, No. 7, 1986. pp. 869-870. doi:10.1109/TAC.1986.1104420
- T. Kaczorek, “Extensions of the Cayley-Hamilton Theorem for 2D Continuous-Discrete Linear Systems,” Applied Mathematics and Computation Sciences, Vol. 4, No. 4, 1994, pp. 507-515.
- N. M. Smart and S. Brunett, “The Algebra of Matrices in n-Dimensional Systems,” IMA Journal of Mathematical Control and Information, Vol. 6, No. 2, 1989, pp. 121-133. doi:10.1093/imamci/6.2.121
- M. Buslowicz and T. Kaczorek, “Reachability and Minimum Energy Control of Positive Linear Discrete-Time Systems with One Delay,” Proceedings of 12th Mediterranean Conference on Control and Automation, KasadesiIzmur, CD ROM, 2004.
- T. Kaczorek, “Linear Control Systems, Vol. I and II,” Research Studies Press, Taunton, 1992-1993.
- B. G. Mcrtizios and M. A. Christodolous, “On the Generalized Cayley-Hamilton Theorem,” IEEE Transactions on Automatic Control, Vol. 31, No. 1, 1986, pp. 156-157.
- N. J. Theodoru, “M-Dimensional Cayley-Hamilton Theorem,” IEEE Transactions on Automatic Control, Vol. 34, No. 5, 1989, pp. 563-565. doi:10.1109/9.24217
- M. Buslowicz, “An Algorithm of Determination of the Quasi-Polynomial of Multivariate Time-Invariant Linear System with Delays Based on State Equations,” Archive of Automatics and Telemechanics, Vol. 36, No. 1, 1981, pp. 125-131.
- M. Buslowicz, “Inversion of Characteristic Matrix of the Time-Delay Systems of Neural Type,” Control Engineering, Vol. 7, No. 4, 1982, pp. 195-210.
- T. Kaczorek, “Extension of the Cayley-Hamilton Theorem for Continuous-Time Systems with Delays,” International Journal of Applied Mathematics and Computer Science, Vol. 15, No. 2, 2005, pp. 231-234.
- T. Kaczorek, “Vectors and Matrices in Automation and Electrotechnics,” Polish Scientific Publishers, Warsaw, 1988.

