Atmospheric and Climate Sciences
Vol.3 No.3(2013), Article ID:34087,11 pages DOI:10.4236/acs.2013.33041
Aquacrop Model Calibration in Potato and Its Use to Estimate Yield Variability under Field Conditions
Facultad de Ciencias Agropecuarias (FCA), Universidad Nacional de Córdoba (UNC), Córdoba, Argentina
Email: *delacasa@agro.unc.edu.ar
Copyright © 2013 Antonio de la Casa et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 23, 2013; revised June 22, 2013; accepted June 30, 2013
Keywords: Potato; Canopy Cover; AquaCrop Model; Soil Water Content
ABSTRACT
AquaCrop model estimates the crop productivity decrease in response to water stress, determining the biomass (B) based on water productivity (WP) and accumulated transpiration (ΣTr); and the yield (Y) is calculated according to B and the harvest index (HI). AquaCrop was evaluated considering different WP values for 2010 late growing season to simulate crop yield of potato (Solanum tuberosum L.) cv. Spunta, in a commercial production field of 9 ha located in the green belt of Cordoba city (31˚30'S, 64˚08'W, 402 m asl), while monitoring in 2009 was used to verify the model. Canopy cover estimation by AquaCrop was adjusted using observed field data obtained from vertical digital photographs acquired at 2.5 m height. WP values of 15.8 and 31.6 (for C3 and C4 species, respectively) and two intermediate values 21 and 26.3 g·m−2 were considered to evaluate the model performance. While linear function between observed tuber yields and estimated by AquaCrop had always a correlation coefficient greater than 0.94 (p < 0.001), using WP = 26.3 and WP =31.6 g·m−2 presented overestimation, whereas with 15.8 g·m−2 had an opposite behavior, while WP = 21 g·m−2 was the value that produced the lowest estimation error. In addition, soil moisture from this estimated value of WP was highly correlated with measured water content in different areas of production field. The verification test shows that while the model slightly underestimates canopy cover, biomass was overestimated. After setting the coefficients of canopy cover development, the AquaCrop crop model estimated adequately potato yield for high production values that are less affected by lack of water, but in both years showed a tendency to overestimate the lowest yields, as was observed for other crops. Meanwhile, the dispersion between the observed and estimated yield was higher in the verification test because the sampling this year was more random.
1. Introduction
Cordoba Province is currently the major potato (Solanum tuberosum L.) producing region of Argentina, and the green belt (gb) of Cordoba city has the largest growing area nationally [1]. Spunta is the more important cultivar used, of Dutch origin and intermediate cycle, with two growing seasons in Córdoba: from August to December (semi-early) and from February to June (late) [2], with irrigated and rainfed yields ranging from 20 to 22 Mg·ha−1 and from 15 to 17 Mg·ha−1, respectively. According to estimates made in different regions of Argentina, there is a considerable difference between current and potential potato yields [3], so there are many possibilities to reduce this productive gap insofar that the limitations will be overcome [4].
The potato crop in the gb of Cordoba is produced by applying traditional agricultural practices, without considering productivity heterogeneity within each field, despite the technological advances that made possible the precision agriculture (PA). This technique consists in making agronomic practices according to the particular requirements of each sector of the field, tending to use the inputs in a rational way, as well as specific recommendations available at the site level [5]. Despite the economic importance of potato crop in the region, there is insufficient information about the PA linked to its production, even in basic issues such as yield spatial variability [6].
Integrating crop simulation models with the producer experience and PA tools, can facilitate the development of strategies for use and management practices adjusted to the condition of each sector in the field and, particularly in those sites with greater restrictions [7]. Producer skill and knowledge of spatial data contribute to identifying areas of the field, to address soil sampling. From this information, models can be applied to estimate crop yield potential and determine the particular restrictions to achieve that potential.
The PA implementation in potato crop, first requires to know the spatial variability, of both productivity as well as properties and processes responsible of yield. By making such assessment directly in a farm, it is possible not only understand broadly the productive variability, but also diagnose the current production situation and the potential deterioration of the environment faced by the productive sector of the cropped area around Cordoba city.
AquaCrop Model
AquaCrop crop model is based on FAO method that estimates crop productivity decrease in response to water stress [8]. AquaCrop has the following characteristics [9]: 1) distinguish evapotranspiration (ET) between crop transpiration (Tr) and soil evaporation (E), 2) considers a simple model of growth and senescence of canopy cover as basis for estimating Tr and to separate it from E, 3) considers that the yield obtained (Y) is a function of biomass (B) and the harvest index (HI), and 4) water stress is evaluated separately by four functions affecting growth and senescence of canopy cover, Tr and HI. By splitting the ET in E and Tr the unproductive use of E in biomass production is avoided, which is important especially during the period when the ground cover is incomplete. The AquaCrop growth engine to estimate B (biomass per unit of accumulated transpiration, g·m−2) per day is:
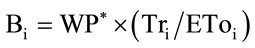 (1)
(1)
where WP* is the water productivity normalized by the evaporative demand of atmosphere, which is defined by the reference evapotranspiration (ETo), and the CO2 atmospheric concentration. This normalization produces water productivity coefficients which tend to be relatively constant under particular climatic conditions [10,11].
As in other crop models, AquaCrop structures the soilplant-atmosphere system by including 1) the soil, by incorporating water and nutrients budgets, 2) the plant, through their processes of growth, development and yield, and 3) the atmosphere, with its thermal regime, rainfall, evaporative demand and carbon dioxide concentration. While it is a generic model, presents specific parameters for different crops, and some of them have a conservative character [9].
Crop models need to be analyzed in its predictive behavior, and adjusted or calibrated prior to more extensive use, particularly when considering conditions of genotype, environment and specific management. In this sense, AquaCrop was been configured and tested in corn [12], and also subject to validation under irrigated and water deficit conditions [13]; parameterized and tested in irrigated and rainfed cotton [14]; compared with other crop models to estimate sunflower growth under different water regimes [15]; and to evaluate the quinoa (Chenopodium quinoa Willd.) yield response to water availability [16].
Unlike other crop models that use the leaf area index as biophysics variable through which the crop interacts with the atmosphere, AquaCrop employs canopy cover and, based thereon, structures the dynamic of growth, water consumption and crop productivity [17]. The model estimates the canopy cover development from an integrated set of three exponential functions throughout the crop cycle, first the coverage value is calculated in the absence of restrictions, which then is adjusted according to the water stress or actual soil nutritional conditions. In most studies of AquaCrop calibration and verification is to be noted that are lacking foliage coverage measurements and, for this reason, assessment of model behavior is implemented with estimated coverage data.
Because the recent appearance of AquaCrop, information about the model performance is relatively scarce, and it is not known if the model has been put operative for potato yet. Although the model includes a set of coefficients to represent crop bioclimatic requirements and tolerances, the global geographic expansion of potato causes a wide range of behaviors and productive responses [18]. Only in Argentina, for all production regions [4] established the possibility of four growing seasons, each one characterized according to their different climatic conditions, soil type, cultural practices and yield level. Thus, the availability of a potato model adapted to local and regional conditions should have a strong impact to project the crop expansion into new regions or analyze any restrictions that should be overcome in the currently production areas. Moreover, it is interesting to evaluate the model performance in the context of productive variability which may present at field conditions [6], where differences of climatic, soil and technological environments are less pronounced and demand more to the predictive ability of the simulation tool.
Within these general guidelines, this work considered two objectives: 1) calibrate the AquaCrop model using data of canopy cover obtained through digital photographs to represent the potato behavior under the environmental conditions of Córdoba green belt, Argentina, 2) analyze the model performance to evaluate production variability in a commercial field in two years under contrasting weather conditions.
2. Material and Methods
2.1. Description of the Study Area
The work was performed in a 9 ha potato (Solanum tuberosum L., cv. Spunta) field of commercial production, during late autumn cycle in 2009 and 2010. The property is located in the green belt of Cordoba city, Argentina (31˚30'S, 64˚08'W, 402 m asl). The soil is classified as Haplustol entic series Manfredi, fine silty, mixed, thermic [19], without limitations for irrigated agriculture.
2.2. Crop Management
According to regular crop practices, the planting was carried out with a density of 6 pl·m−2. The 2009 growing season of potato was carry on from February 9 to May 29. The crop was fertilized with 260 kg·ha−1 NPK (20-14-3) at planting with the supplement of Mg and S and, in addition, was watered by furrows on 2 moments: at 58 (07/ 04/2009) and 71 (20/04/2009) days after planting, applying 25 mm at each date. The experiment consisted of a rectangular grid of 5 × 5 sampling sites spaced 47 m in the N-S direction and 44 m following the irrigation furrows (E-W).
The late cycle of 2010 was extended from 16 February to 29 May. The crop was fertilized at planting with 250 kg·ha−1 NPK (20-17-3) and the addition of Mg and S, and later with 22-0-0 and the supplement of S, Ca and Mg. Under these conditions of high fertilization level, productive losses due to nutrient deficiency were not considered in the simulation. Meanwhile, during the crop cycle received a surface irrigation of 20 mm at 43 days after planting (31/03/2010). The sampling grid in this year was square, with 3 rows × 3 columns spaced every 70 m.
2.3. Field Measurements
2.3.1. Canopy Cover
In 2009 and with an average frequency of 12 days, a vertical photography (at 1.2 m height) was taking to calculate the canopy cover (CC) near (to the west) of each grid node. In 2010, at each node of the grid an approximately 4 m2 sampling was performed acquiring nine vertical photographs (taken at 2.5 m above the crop) in different positions equidistant to obtain the mean value of CC by date with an average frequency of 12 days. In both years, the crop cover was obtained according to [20] and [21], from a digital procedure which determines the presence of vegetation above ground by performing the colorimetric decomposition of the image in the visible range [22]. For the purposes of classification, in each pixel of the image is performed the green (g) and red (r) bands ratio, and vegetation was considered when g/r was greater than 1.05 and soil in the contrary case. [23] determined that the ground cover calculated in this way do not differ from those obtained by the maximum likelihood method and is easier to implement.
2.3.2. Total Biomass
In 2009, two sectors, one between nodes 12 and 13 and the other between the nodes 21 and 22, with the same frequency than for crop cover, 2 samples of 1 m2 of total biomass were taken to obtain total dry matter.
2.3.3. Crop Yield
In 2009 all tubers were harvested in 1 m2 of each node. The yield of 2010 was obtained collecting all tubers in 1 m2 of 6 places equidistant from each node. To express crop yield as dry matter, a ratio dry/fresh weight of 0.2 was used [4].
2.4. Information Used by AquaCrop
The description of the data is performed according to file structure required to run AquaCrop model.
2.4.1. Soil Information
According to the profile description for the soils of the region [24], the file was integrated with three soil horizons whose limits of availability water are shown in Table 1. Using Soil Water characteristics program [25], and considering the low organic matter due continuous tillage, the field capacity value (FC) was reduced in A horizon, while the abundant fertilization justifies wilting point values (WP) slightly higher compared to those presented by [24].
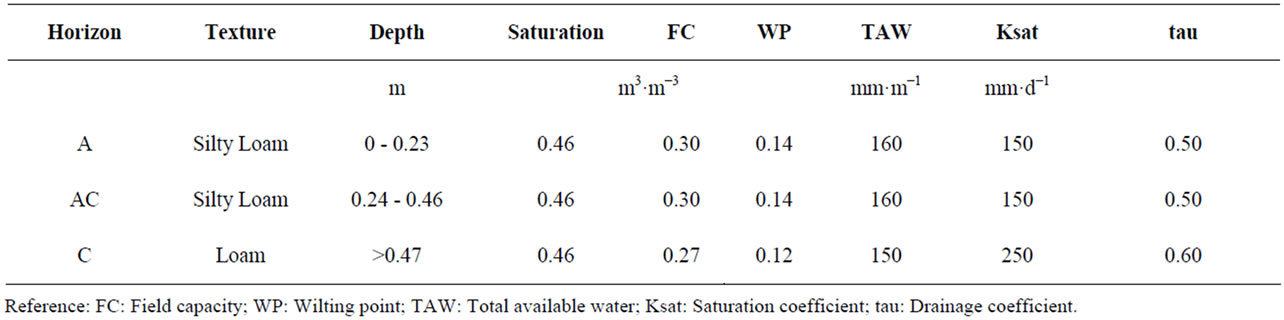
Table 1. Soil properties used to represent the soil modal green belt (gb) of Cordoba City. These data constitute the file soil used by AquaCrop model for late potato season in 2009 and 2010.
2.4.2. Climate
Meteorological data were obtained from an automatic monitoring station located 9 km from the site. The station provides hourly records of solar radiation, precipitation, temperature and relative humidity. From hourly records of temperature and humidity, daily maximum and minimum values were obtained of both elements. Similarly, daily radiation and precipitation data were accumulated. With the daily values of solar radiation, maximum and minimum temperature and maximum and minimum relative humidity the reference evapotranspiration (ETo) was calculated by the Penman-Monteith method, using EToCalc v3.1 software [26].
Weather files were created for each year from daily values of rain, reference evapotranspiration, maximum and minimum temperature and atmospheric CO2 concentration, according to the program default file (AquaCrop considers 369.47 ppmv as reference level, which is the average of the atmospheric concentration of CO2 in 2000 at Mauna Loa observatory, Hawaii).
2.4.3. Crop Management
According to potato production in the gb of Cordoba city, the model considered in both years a proportion of ground covered by stubble of only 4%, which practically does not limit the evaporation rate from the soil. Furthermore, the ground was systemized for furrow irrigation so that restricted flow is not considered, nor are water embankments. In order to estimate the surface runoff, a curve number 65 was used [27]. While not considered limitations on fertility, irrigation water supply was simulated incorporating water amounts listed above for each of the dates.
2.4.4. Model Parameters
Coefficients and conservative parameters (generics) that AquaCrop uses to represent crop performance against water stress conditions were modified slightly so that the crop was considered moderately tolerant to water stress for canopy expansion and stomatal closure, keeping unchanged the remaining (moderately tolerant to early canopy senescence and stress by aeration).
2.5. Calibration and Validation
The AquaCrop calibration strategy to reproduce the particular potato production conditions of the gb of Cordoba was implemented considering observed ground cover data throughout the cycle against those estimates by the model. Model calibration for late season potato crop was made from spatially distributed data observed in 2010, due this year the sampling was more intensive, while the 2009 data obtained under less intensive sampling conditions, were used for validation. Furthermore, while in 2010 the potato crop had more favorable conditions for growth, so that canopy cover was relatively uniform and reached maximum values above 90%, in 2009 the “top necrosis” disease (caused by the Tomato Spotted Wilt Virus—TSWV) restricted ground cover in different sectors across the field and thus increased the spatial yield variability.
The canopy cover (CC) is a relevant biophysical parameter that represents the ability of a crop for intercepting solar radiation, as well as to discriminate ETo between crop transpired water (Tr) from soil evaporated water. To obtain the CC that expresses a potential growth value, we proceeded according to [9], who represents the development of the cover by coupling three exponential equations:
 (2)
(2)
where: CC is the canopy cover at time t, expressed as a fraction ground cover; CC0 is the initial size of the canopy (at t = 0) in fraction, and CGC is the growth rate of the canopy in fraction per day, which is a constant value for a crop under optimal growth conditions and is modulated by water stress effect.
This function represents the exponential growth of the crop during the first instance after emergence, when growth is proportional to existing size of CC. At the moment that the plants begin to shade each other, development progresses according to second stage, where CC follows an exponential decay rate, according to:
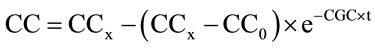 (3)
(3)
where:  is the maximum coverage for optimal growing conditions.
is the maximum coverage for optimal growing conditions.
As the crop approaches maturity, CC begins to show a decline phase due to general leaf senescence. The model describes this third stage according to following expression:
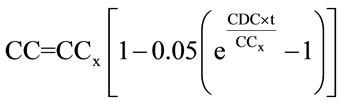 (4)
(4)
where: CDC is the canopy decline coefficient (in fraction per day reduction), and t is the time from the onset of senescence.
Due to the absence of local or regional determinations of water productivity (WP) in potato, the calibration consisted in obtain its value using AquaCrop basic information, considering firstly the range of typical model values for C3 and C4 crops metabolism.
3. Results and Discussion
3.1. Year 2010
Figure 1(a) shows canopy cover (CC) variation during the late potato growing season of 2010 in one of the 9 sectors of the commercial field. While dots show observations of CC determined from digital photographs at different times of the crop cycle, the continuous line corresponds to the values estimated by AquaCrop for weather, soil and crop management conditions of late potato growing season in the Cordoba gb. The development coefficients of CC that were used, obtained by trial and error, are presented in Table 2.
The simulated function describes the canopy cover observed very closely throughout the crop cycle, so the linear fit between the two variables, as shown in Figure 1(b), presents a slope very close to one, while the value of the intercept approaches zero. This analysis was extended to the rest of field and the results obtained are presented in Table 2. As in the Sector 1.1, the remaining nodes analyzed have linear functions that not differ statistically from the identity function.
In order to obtain a characteristic value of water productivity (WP) for environmental and technological conditions of Córdoba green belt, the final yield of potato crop cultivar Spunta was estimated considering different values. Then a relationship was established between the
 (a)
(a)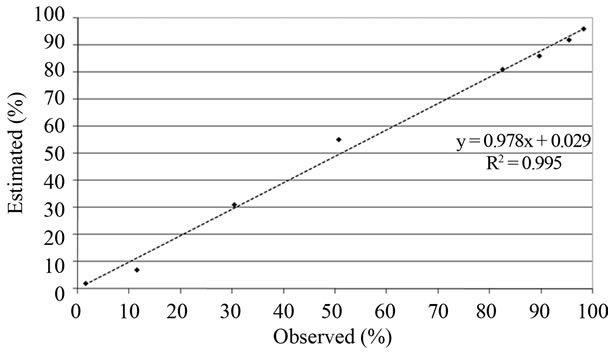 (b)
(b)
Figure 1. (a) Canopy cover variation observed (dots) and estimated by AquaCrop (dash line) with respect to days after planting in node 1.1 in 2010. Vertical bars indicate +/− one standard deviation; (b) Relationship between observed and estimated canopy cover.
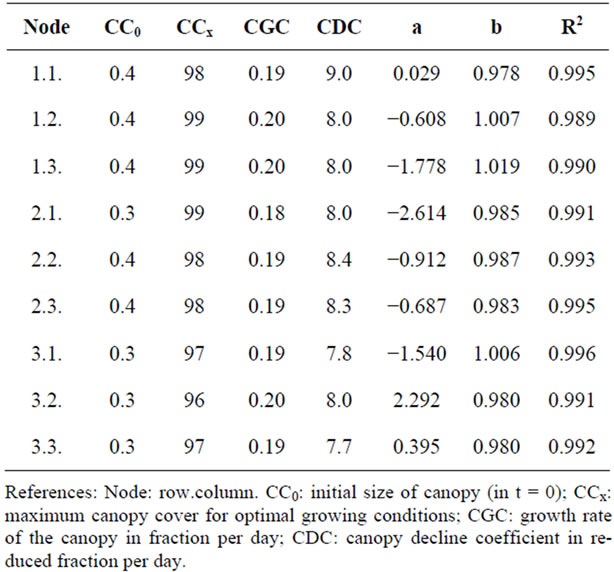
Table 2. Development coefficients of canopy cover model for potato crop used by AquaCrop, and regression (a: intercept, b: slope) and determination (R2) coefficients for the relationship between observed and estimated canopy cover for each node in 2010.
final tuber yields observed and estimated by AquaCrop for different levels of WP, as shown in Figure 2.
The adjustment function between the observed and calculated values in all cases presents a determination coefficient equal to 0.9 (p < 0.001), but with WP = 26.3 g·m−2 and WP = 31, 6 g·m−2 occurs a marked overestimation, and when employing 15.8 g·m−2 the behavior is opposite, meanwhile using WP = 21 g·m−2 produces the lowest estimation error. As is the case with radiation use efficiency (RUE) values [28], the water productivity in potato crop also presents intermediate values between those characteristic for C3 and C4 species.
Evaluations about radiation use efficiency in potato assigned this crop the highest value within the C3, even similar to C4 species like corn, levels that have also been reported for cv Spunta under environmental conditions Córdoba green belt [29] [30]. Based on this argument, and according to the results obtained here, it is considered appropriate to use a value of water productivity of 21 g·m−2, intermediate between those proposes by the model for C3 and C4 species. Anyway, overestimation of yields increases when observed productivity are lower, suggesting, like the first evaluations in other crops [13], that AquaCrop behavior is more suitable under greater water supply conditions, but tends to estimate incorrectly the biomass or yield under water stress conditions [31].
Having established estimated conditions of CC similar to the measured, the difference in coverage that occurs in different sectors of the commercial field should explain, according to the logic of the model, the productivity levels achieved at each site particularly. The different sizes of crop transpiration surface also should be reflected in a particular soil moisture condition during the growing season, specially the water consumption (evaporation and transpiration), because the replenishment (rain and irrigation) is assumed uniform in the field. Considering soil moisture as a control variable, and analyzing the degree of correspondence between observed and estimated by AquaCrop, Figure 3 shows the variation experienced by the soil water content along the growing season in 1.1 node.
The water content variation estimated by AquaCrop for the layer between 0.15 and 0.35 m, represents this dynamic in an appropriate way for the node 1.1, while the last measured value has a more significant underestimation. The analysis of the relationship between observed and estimated values was extended to the other nodes in the field, obtaining the linear regression and correlation coefficients presented in Table 3.
The estimated and observed values of soil moisture in each sector present a significant linear relationship (p < 0.01), with the intercept being different from zero and the slope greater than 1 which, except for node 3.3, shows some inconsistency. The spatial distribution of errors between the mean tuber yield observed and estimates by AquaCrop for the nodes of the sampling grid are shown in Figure 4. It shows that there is a trend of the error to decrease in the field, being consistently higher the error obtained on the nodes located on row 3 (north of the field).
Similarly, as shown in Table 4, the relationship between potato yields and observed moisture condition in each sector presents a correlation coefficient always positive, that has statistical significance (p < 0.05) in 2 of 6 sampling dates.
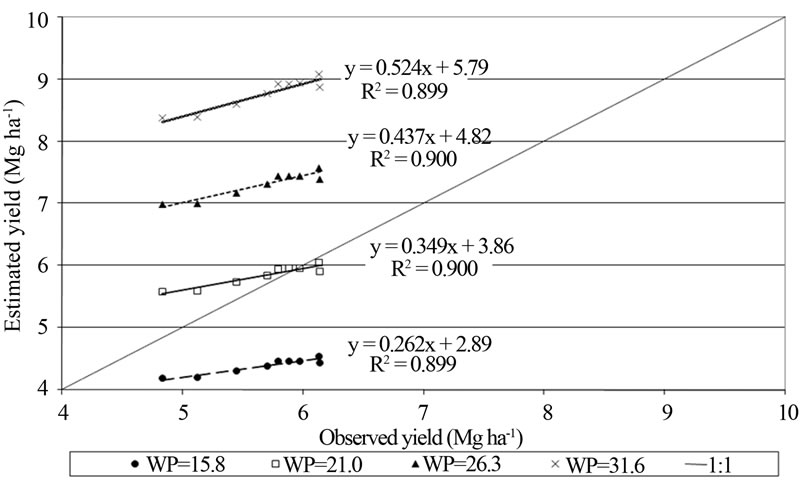
Figure 2. Relationship between observed tuber yield (dry matter) in different nodes of a production field of Córdoba green belt monitored in 2010, and those estimated by AquaCrop considering different water productivity values (WP, g·m−2).
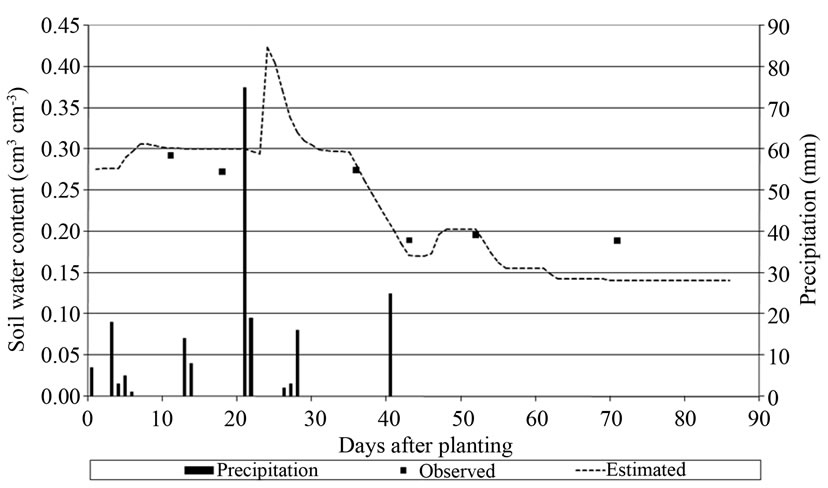
Figure 3. Soil water content observed (0.20 - 0.30 m) and estimated (0.15 - 0.35 m) by AquaCrop for the node 1.1. in 2010 in relation to days after planting. Also presented daily precipitation records in bar graph.
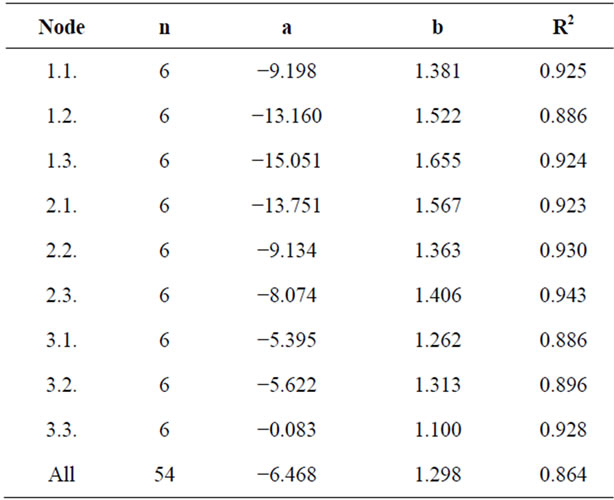
Table 3. Coefficients of regression (a: intercept; b: slope) and determination (R2) for the relationship between soil water content observed in 0.20 - 0.30 m layer and estimated by AquaCrop in 0.15 - 0.35 m layer, for each of 9 nodes in 2010.
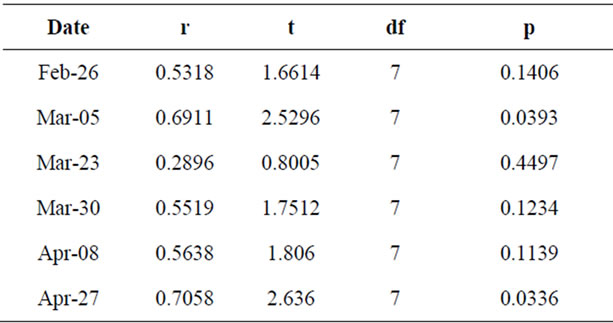
Table 4. Coefficients of correlation (r), t value and its probability (p) for the linear relationship between the soil moisture content and tuber yield in different dates of growing season.
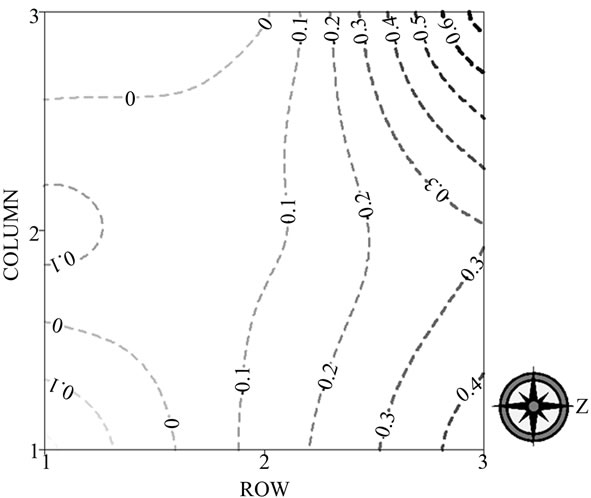
Figure 4. Spatial variation of the error (Mg·ha−1) between observed and estimated yields with WP = 21 g·m−2 in 2010.
3.2. Year 2009
The potato crop was monitored in the same field of commercial production of 2010, and was used as a control test to verify the predictive performance of AquaCrop. Sampling was less intensive as canopy cover was determined from a single photograph obtained only on the nodes of grid sampling. Furthermore, due to the impact of the Black Death, a disease that was so variable in the field, the canopy cover presented a higher variability compared to 2010. The variables used to evaluate AquaCrop, additionally to CC, were, first, the biomass produced from measurements taken during the growth season into two sectors of the potato field (between nodes 1.2. and 1.3. and between nodes 2.1. and 2.2.) and, in second term, the yield of tubers that were harvested on each of the 25 nodes.
With respect to dry matter production, Figure 5 shows the variation of canopy cover and the biomass obtained along crop season in two sectors of the field.
It shows a strong contrast between the two sectors monitored, with maximum coverage values below 40% in the 1.2. - 1.3. sector and that exceeds 80% in 2.1. - 2.2., what characterizes the greater heterogeneity of crop production in 2009. Consistent with the difference between canopy coverage, total crop biomass also shows a significant difference between the two sites.
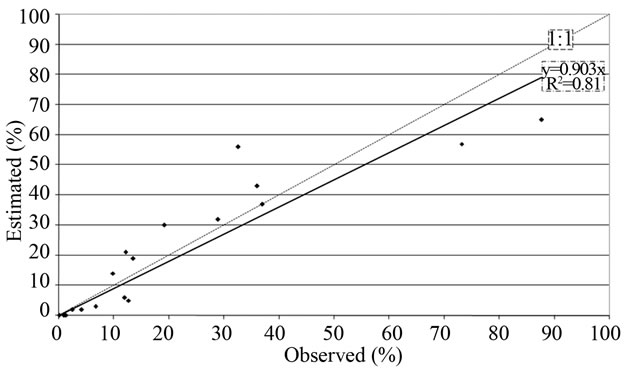
Figure 6 shows the correlation and regression analysis between CC and biomass values observed and estimated by AquaCrop for both sectors simultaneously (with initial conditions of soil moisture at field capacity). The results are contradictory since, while the regression line of canopy cover approximates the identity function, Although the dispersion is somewhat high (R2 = 0.81) and a trend toward underestimation for higher values, the figure for dry matter has a slope of 1.4, with a somewhat lower level of dispersion, which means that the model systematically overestimates measurements. As seen in the canopy cover values of Figure 5, the incidence of “top necrosis” disease produced a marked retardation of cover growth between 30 and 40 days after planting, which explains the increase of dispersion between the observed canopy cover and estimated by model.
The aptitude of AquaCrop to estimate potato yield was verified in the first instance assimilating canopy cover estimated by the model in the absence of growth restrictions and the observations obtained in the sampling grid. For this purpose, the development coefficients of canopy cover were determined using the model, solving its value by trial and error based on a linear fit function between observed and estimated, with the results shown in Table 5. Although the R2 values obtained are high and exceeds 0.9 in 20 of 25 cases, and the slopes do not differ significantly than 1, assuring the similarity between calculated and observed, in other cases the observed curves of canopy cover presented significant alteration making difficult to achieve greater approximation.
Observed and estimated canopy cover variation throughout the growing season for nodes 2.4. and 4.4. of 2009 is shown in Figure 7.
The relationship between observed tuber yield in each 1 m2 plots in the nodes of the sampling grid and those calculated with AquaCrop is shown in Figure 8. The estimates were made considering initial moisture content at field capacity (FC), to avoid the influence of this factor so that the difference in yield in the field is determined only by changes in coverage.
Both for 2009 and 2010 late potato growing season, the results confirm that the duration of canopy cover (coverage integration along the cycle) is a good indicator of the productive capacity of the potato crop [30,32], so that its monitoring during the crop cycle can generate useful information to plan or to establish eventually precision agriculture, or to establish areas of located management [33]. Because of the less intensive sampling and probably as a consequence of the “top necrosis” disease, in 2009 there was a significant variability in the commercial field, which is only partially explained by the model. However, it is considered that this result can be more linked to spatial variability analysis of the production field because, unlike 2010, is performed directly at level of unit area. Similarly, while it is considered necessary produce further evidence to confirm the water use efficiency or water productivity by the potato cv Spunta, estimates produced by AquaCrop seem to be consistent to evaluate the spatial variability of the productivity under cultivation regime of Córdoba green belt.
4. Conclusions
Once the coefficients of canopy cover development are adjusted, AquaCrop estimated adequately crop yield of

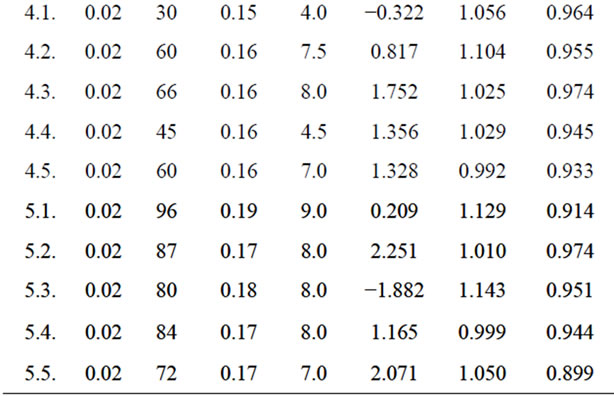
Table 5. Coefficients of canopy cover development used by AquaCrop model to estimate potato coverage and coefficients of regression (a: intercept, b: slope) and determination (R2) between observed and estimated values at the nodes of the sampling grid in 2009.

Figure 5. Total dry matter (DM) and canopy cover variation according to the days after planting in two sectors of field production in 2009.
 (a)
(a)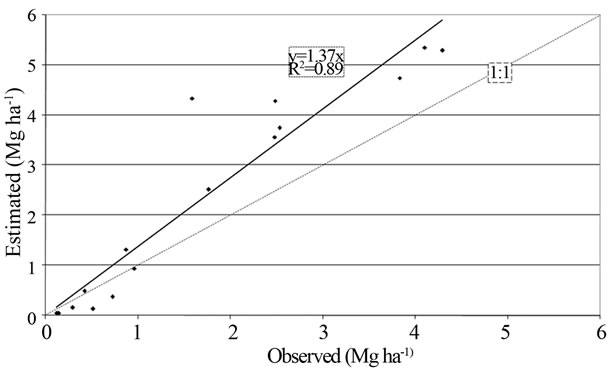 (b)
(b)
Figure 6. Relationship between observed canopy cover (a) and biomass (b) and those estimated by AquaCrop in sectors 12 - 13 and 21 - 22 of the production field in 2009. The dashed line is the 1:1 function.
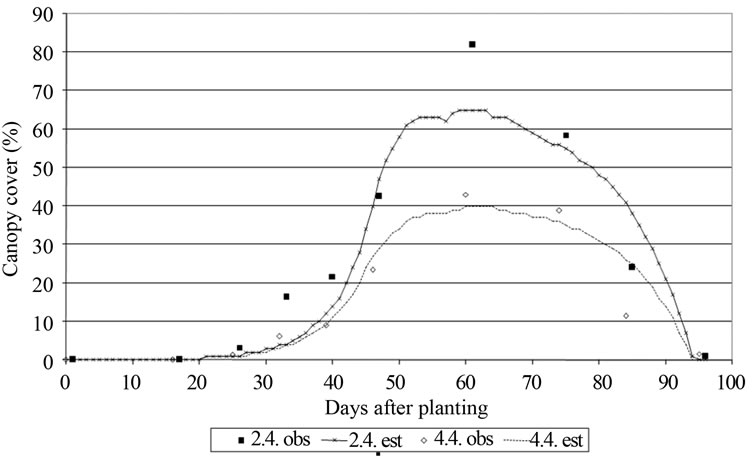
Figure 7. Canopy cover observed and estimated by AquaCrop in relation to days after planting in 2 nodes (2.4 y 4.4) in 2009.
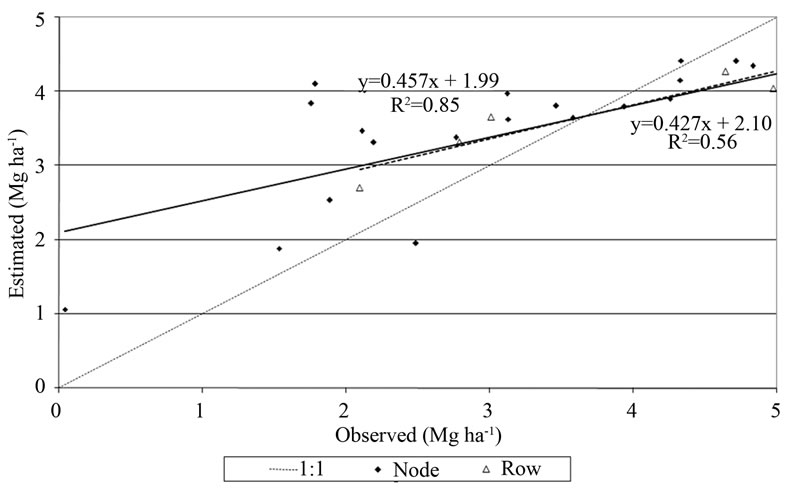
Figure 8. Tuber yields (dry weight) observed and estimated with AquaCrop at 25 nodes and the mean value per row in 2009.
potato, particularly for high production levels. For the environmental, cultural and technological conditions of Córdoba greenbelt, water productivity in potato was 21 g·m−2, intermediate value for species of C3 and C4 metabolism. This water productivity level proposed to represent potato crop cv Spunta under autumn season conditions of Córdoba greenbelt, can be considered acceptable as a first approximation insofar the productivity levels calculated are similar to those observed.
AquaCrop estimated adequately the evolution of soil water content of the potato crop during the growing season, as well as the spatial distribution of productivity was simulated consistent with the observed values. The model performance can be improved by adjusting the differences of the input data (irrigation, drainage, bulk density) in different sectors of the commercial field.
REFERENCES
- M. Mosciaro, “Caracterización de la Producción y Comercialización de Papa en Argentina,” Área de Economía y Sociología Rural, EEA-INTA, Balcarce, 2004.
- D. O. Caldiz and P. C. Struik, “Survey of Potato Production and Possible Yield Constraints in Argentina,” Potato Research, Vol. 42, No. 1, 1999, pp. 51-71. doi:10.1007/BF02358391
- J. Kadaja and H. Tooming, “Potato Production Model Based on Principle of Maximum Plant Productivity,” Agricultural and Forest Meteorology, Vol. 127, No. 1-2, 2004, pp. 17-33. doi:10.1016/j.agrformet.2004.08.003
- D. O. Caldiz, F. J. Gaspari, A. J. Haverkort and P. C. Struik, “Agro-Ecological Zoning and Potential Yield of Single or Double Cropping of Potato in Argentina,” Agricultural and Forest Meteorology, Vol. 109, No. 4, 2001, pp. 311-320. doi:10.1016/S0168-1923(01)00231-3
- F. J. Pierce and P. Novak, “Aspects of Precision Agriculture,” Advances in Agronomy, Vol. 67, 1999, pp. 1-85. doi:10.1016/S0065-2113(08)60513-1
- E. A. Po, S. S. Snapp and A. Kravchenko, “Potato Yield Variability across the Landscape,” Agronomy Journal, Vol. 102, No. 3, 2010, pp. 885-894. doi:10.2134/agronj2009.0424
- Y. M. Oliver, M. J. Robertson and M. T. F. Wongbet, “Integrating Farmer Knowledge, Precision Agriculture Tools, and Crop Simulation Modelling to Evaluate Management Options for Poor-Performing Patches in Cropping Fields,” European Journal of Agronomy, Vol. 32, 2010, pp. 40-50. doi:10.1016/j.eja.2009.05.002
- J. Doorenbos and A. H. Kassam, “Yield Response to Water, FAO Irrigation and Drainage Paper No. 33,” Food and Agriculture Organization of United Nations, Rome, 1979.
- P. Steduto, T. C. Hsiao, D. Raes and E. Fereres, “AquaCrop—The FAO Crop Model for Predicting Yield Response to Water: I. Concepts and Underlying Principles,” Agronomy Journal, Vol. 101, No. 3, 2009, pp. 426-437. doi:10.2134/agronj2008.0139s
- C. B. Tanner and T. R. Sinclair, “Efficient Water Use in Crop Production,” In: H. M. Taylor, et al., Ed., Limitations to Water Use in Crop Production, ASA, CSSA, and SSSA, Madison, 1983.
- P. Steduto, T. C. Hsiao and E. Fereres, “On the Conservative Behavior of Biomass Water Productivity,” Irrigation Science, Vol. 25, No. 3, 2007, pp. 189-207. doi:10.1007/s00271-007-0064-1
- T. C. Hsiao, L. K. Heng, P. Steduto, B. Rojas-Lara, D. Raes and E. Fereres, “AquaCrop—The FAO Crop Model for Predicting Yield Response to Water: III. Model Parameterization and Testing for Maize,” Agronomy Journal, Vol. 101, No. 3, 2009, pp. 448-459. doi:10.2134/agronj2008.0218s
- L. K. Heng, S. R. Evett, T. A. Howell and T. C. Hsiao, “Calibration and Testing of FAO AquaCrop Model for Rainfed and Irrigated Maize,” Agronomy Journal, Vol. 101, No. 3, 2009, pp. 488-498. doi:10.2134/agronj2008.0029xs
- H. J. Farahani, G. Izzi, P. Steduto and T. Y. Oweis, “Parameterization and Evaluation of AquaCrop for Full and Deficit Irrigated Cotton,” Agronomy Journal, Vol. 101, 2009, pp. 469-476. doi:10.2134/agronj2008.0182s
- M. R. Todorovic, R. Albrizio, L. Zivotic, M. T. Abi Saab, C. Stöckle and P. Steduto, “Assessment of AquaCrop, CropSyst, and WOFOST Models in the Simulation of Sunflower Growth under Different Water Regimes,” Agronomy Journal, Vol. 101, No. 3, 2009, pp. 509-521. doi:10.2134/agronj2008.0166s
- S. Geerts, D. Raes, M. Garcia, R. Miranda, J. A. Cusicanqui, C. Taboada, J. Mendoza, R. Huanca, A. Mamani, O. Condori, J. Mamani, B. Morales, V. Osco and P. Steduto, “Simulating Yield Response to Water of Quinoa (Chenopodium quinoa Willd.) with FAO-AquaCrop,” Agronomy Journal, Vol. 101, No. 3, 2009, pp. 499-508. doi:10.2134/agronj2008.0137s
- D. Raes, P. Steduto, T. C. Hsiao and E. Fereres, “AquaCrop—The FAO Crop Model to Predict Yield Response to Water: II Main Algorithms and Software Description,” Agronomy Journal, Vol. 101, No. 3, 2009, pp. 438-447. doi:10.2134/agronj2008.0140s
- P. L. Kooman, M. Fahem, P. Tegera and A. J. Haverkort, “Effects of Climate on Different Potato Genotypes. 1. Radiation Interception, Total and Tuber Dry Matter Production,” European Journal of Agronomy, Vol. 5, 1996, pp. 193-205. doi:10.1016/S1161-0301(96)02031-X
- B. Jarsún, J. Gorgas, E. Zamora, H. Bosnero, E. Lovera, A. Ravelo and J. Tassile, “Los Suelos de Córdoba,” Agencia Córdoba Ambiente e Instituto Nacional de Tecnología Agropecuaria, EEA Manfredi, Córdoba, 2006.
- F. J. Adamsen, P. J. Pinter Jr., E. M. Barnes, R. L. La Morte, G. W. Wall, S. W. Leavitt and B. A. Kimball, “Measuring Wheat Senescence with a Digital Camera,” Crop Science, Vol. 39, No. 3, 1999, pp. 719-724. doi:10.2135/cropsci1999.0011183X003900030019x
- A. A. Gitelson, Y. J. Kaufman, R. Stark and D. Rundquist, “Novel Algorithms for Remote Estimation of Vegetation Fraction,” Remote Sensing of Environment, Vol. 80, No. 1, 2002, pp. 76-87. doi:10.1016/S0034-4257(01)00289-9
- Y. Li, D. Chen, C. N. Walker and J. F. Angus, “Estimating the Nitrogen Status of Crops Using a Digital Camera,” Field Crops Research, Vol. 118, No. 2, 2010, pp. 221-227. doi:10.1016/j.fcr.2010.05.011
- A. de la Casa, G. Ovando, L. Bressanini, Á. Rodríguez and J. Martínez, “Determinación de la Fracción de Suelo Cubierta con el Follaje de Papa a Partir del Cociente Entre Bandas de Fotografías Digitales,” Actas de la XIII Reunión Argentina y VI Latinoamericana de Agrometeorología, Bahía Blanca, Buenos Aires, 2010.
- J. D. Dardanelli, O. A. Bachmeier, R. Sereno and R. Gil, “Rooting Depth and Soil Water Extraction Patterns of Different Crops in a Silty Loam Haplustoll,” Field Crop Research, Vol. 54, 1997, pp. 29-38. doi:10.1016/S0378-4290(97)00017-8
- K. E. Saxton and W. J. Rawls, “Soil Water Characteristics by Texture and Organic Matter for Hydrologic Solutions,” Soil Science Society of America Proceedings of Annual Conference, Seattle, 2004.
- D. Raes, “ETo Calculator v3.1,” Land and Water Digital Media Series No. 36, Food and Agriculture Organization of United Nations, Rome, 2009.
- Soil Conservation Service, “Estimation of Direct Runoff from Storm Rainfall,” In: National Engineering Handbook, Soil Conservation Service, USDA, Washington DC, 1964.
- T. R. Sinclair and R. C. Muchow, “Radiation Use Efficiency,” Advances in Agronomy, Vol. 65, 1999, pp. 215- 265. doi:10.1016/S0065-2113(08)60914-1
- A. de la Casa, G. Ovando, L. Bressanini, Á. Rodríguez and J. Martínez, “Uso del Índice de Área Foliar y del Porcentaje de Cobertura del Suelo Para Estimar la Radiación Interceptada en Papa,” Agricultura Técnica (Chile), Vol. 67, 2007, pp. 78-85.
- A. de la Casa, G. Ovando, L. Bressanini, J. Martínez and Á. Rodríguez, “Eficiencia en el Uso de la Radiación en Papa Estimada a Partir de la Cobertura del Follaje,” Agriscientia, Vol. 26, 2011, pp. 21-30.
- S. R. Evett and J. A. Tolk, “Introduction: Can Water Use Efficiency Be Modeled Well Enough to Impact Crop Management?” Agronomy Journal, Vol. 101, No. 3, 2009, pp. 423-425. doi:10.2134/agronj2009.0038xs
- N. S. Boyd, R. Gordon and R. C. Martin, “Relationship between Leaf Area Index and Ground Cover in Potato under Different Management Conditions,” Potato Research, Vol. 45, No. 2, 2002, pp. 117-129. doi:10.1007/BF02736107
- A. Hornung, R. Khosla, R. Reich, D. Inman and D. G. Westfall, “Comparison of Site-Specific Management Zones: Soil-Color-Based and Yield-Based,” Agronomy Journal, Vol. 98, No. 2, 2006, pp. 407-415. doi:10.2134/agronj2005.0240
NOTES
*Corresponding author.

