International Journal of Astronomy and Astrophysics
Vol.3 No.3(2013), Article ID:36524,26 pages DOI:10.4236/ijaa.2013.33037
Dark Energy Explained via the Hawking-Hartle Quantum Wave and the Topology of Cosmic Crystallography
1Department of Physics, University of Alexandria, Alexandria, Egypt
2Department of Mathematics, University of Cairo, Cairo, Egypt
Email: Chaossf@aol.com
Copyright © 2013 Mohamed S. El Naschie, Atef Helal. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 22, 2013; revised July 21, 2013; accepted July 28, 2013
Keywords: Doubly Special Relativity; Week’s Manifold; Experimental Test of Einstein’s Relativity; Witten’s M-Theory; Ordinary Energy of the Quantum Particle; Hawking-Hartle Wave of Cosmos; Crystallographic Symmetry Groups; Revising Special Relativity
ABSTRACT
The aim of the present paper is to explain and accurately calculate the missing dark energy density of the cosmos by scaling the Planck scale and using the methodology of the relatively novel discipline of cosmic crystallography and Hawking-Hartle quantum wave solution of Wheeler-DeWitt equation. Following this road we arrive at a modified version of Einstein’s energy mass relation E = mc2 which predicts a cosmological energy density in astonishing accord with the WMAP and supernova measurements and analysis. We develop non-constructively what may be termed super symmetric Penrose fractal tiling and find that the isomorphic length of this tiling is equal to the self affinity radius of a universe which resembles an 11 dimensional Hilbert cube or a fractal M-theory with a Hausdorff dimension 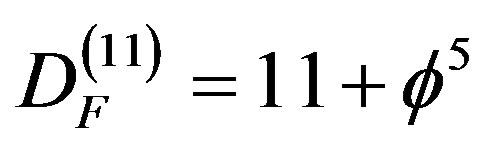 where
where . It then turns out that the correct maximal quantum relativity energy-mass equation for intergalactic scales is a simple relativistic scaling, in the sense of Weyl-Nottale, of Einstein’s classical equation, namely EQR = (1/2)(1/
. It then turns out that the correct maximal quantum relativity energy-mass equation for intergalactic scales is a simple relativistic scaling, in the sense of Weyl-Nottale, of Einstein’s classical equation, namely EQR = (1/2)(1/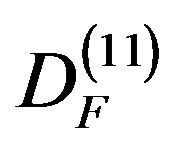 ) moc2 = 0.0450849 mc2 and that this energy is the ordinary measurable energy density of the quantum particle. This means that almost 95.5% of the energy of the cosmos is dark energy which by quantum particle-wave duality is the absolute value of the energy of the quantum wave and is proportional to the square of the curvature of the curled dimension of spacetime namely
) moc2 = 0.0450849 mc2 and that this energy is the ordinary measurable energy density of the quantum particle. This means that almost 95.5% of the energy of the cosmos is dark energy which by quantum particle-wave duality is the absolute value of the energy of the quantum wave and is proportional to the square of the curvature of the curled dimension of spacetime namely  where
where  and
and 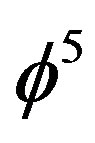 is Hardy’s probability of quantum entanglement. Because of the quantum wave collapse on measurement this energy cannot be measured using our current technologies. The same result is obtained by involving all the 17 Stein spaces corresponding to 17 types of the wallpaper groups as well as the
is Hardy’s probability of quantum entanglement. Because of the quantum wave collapse on measurement this energy cannot be measured using our current technologies. The same result is obtained by involving all the 17 Stein spaces corresponding to 17 types of the wallpaper groups as well as the  three dimensional crystallographic group which gives the number of the first level of massless particle-like states in Heterotic string theory. All these diverse subjects find here a unified view point leading to the same result regarding the missing dark energy of the universe, which turned out to by synonymous with the absolute value of the energy of the Hawking-Hartle quantum wave solution of Wheeler-DeWitt equation while ordinary energy is the energy of the quantum particle into which the Hawking-Hartle wave collapse at cosmic energy measurement. In other words it is in the very act of measurement which causes our inability to measure the “Dark energy of the quantum wave” in any direct way. The only hope if any to detect dark energy and utilize it in nuclear reactors is future development of sophisticated quantum wave non-demolition measurement instruments.
three dimensional crystallographic group which gives the number of the first level of massless particle-like states in Heterotic string theory. All these diverse subjects find here a unified view point leading to the same result regarding the missing dark energy of the universe, which turned out to by synonymous with the absolute value of the energy of the Hawking-Hartle quantum wave solution of Wheeler-DeWitt equation while ordinary energy is the energy of the quantum particle into which the Hawking-Hartle wave collapse at cosmic energy measurement. In other words it is in the very act of measurement which causes our inability to measure the “Dark energy of the quantum wave” in any direct way. The only hope if any to detect dark energy and utilize it in nuclear reactors is future development of sophisticated quantum wave non-demolition measurement instruments.
1. Introduction
The present work is mainly concerned with elucidating dark energy [1-5] by means of an accurate mathematical formulation which leads to a prediction in complete agreement with the cosmological measurement [5-7]. The task seems at first sight to be clearly very difficult.
The more reason for us to be considerably surprised is when we found out how simple and straight forward it is, particularly when adopting the methodology of what has come to be known in recent years as cosmic crystallography [6-8]. Thus in our analysis we will rely upon the quasi crystal model of Penrose [4-9] after making it super symmetric [10,11] as well as different higher dimensional versions of the classical Islamic tiling groups [12], i.e. the 17 wallpaper groups corresponding to 17 two and three Stein spaces [13]. In turn these Stein spaces are close cousins of compact and non-compact fundamental Lie symmetry groups [12-15] as well as the 8064 classical first massless state-like particles of Heterotic string theory [7-28]. In addition we show that our cosmos possesses a clopen topology and is pseudo flat on average. To facilitate quick understanding, our main results are summarized in Figures 1-14 with detailed explanation in the captions. In particular the main quantitative results obtained using advanced transfinite set theory are also confirmed using the exact solution of the hydrogen atom (see Figure 13) and we give various plausibility explanations of antigravity using simple demonstrations (see Figure 14).

Figure 1. Transfinite set theoretical formulation of quantum physics.
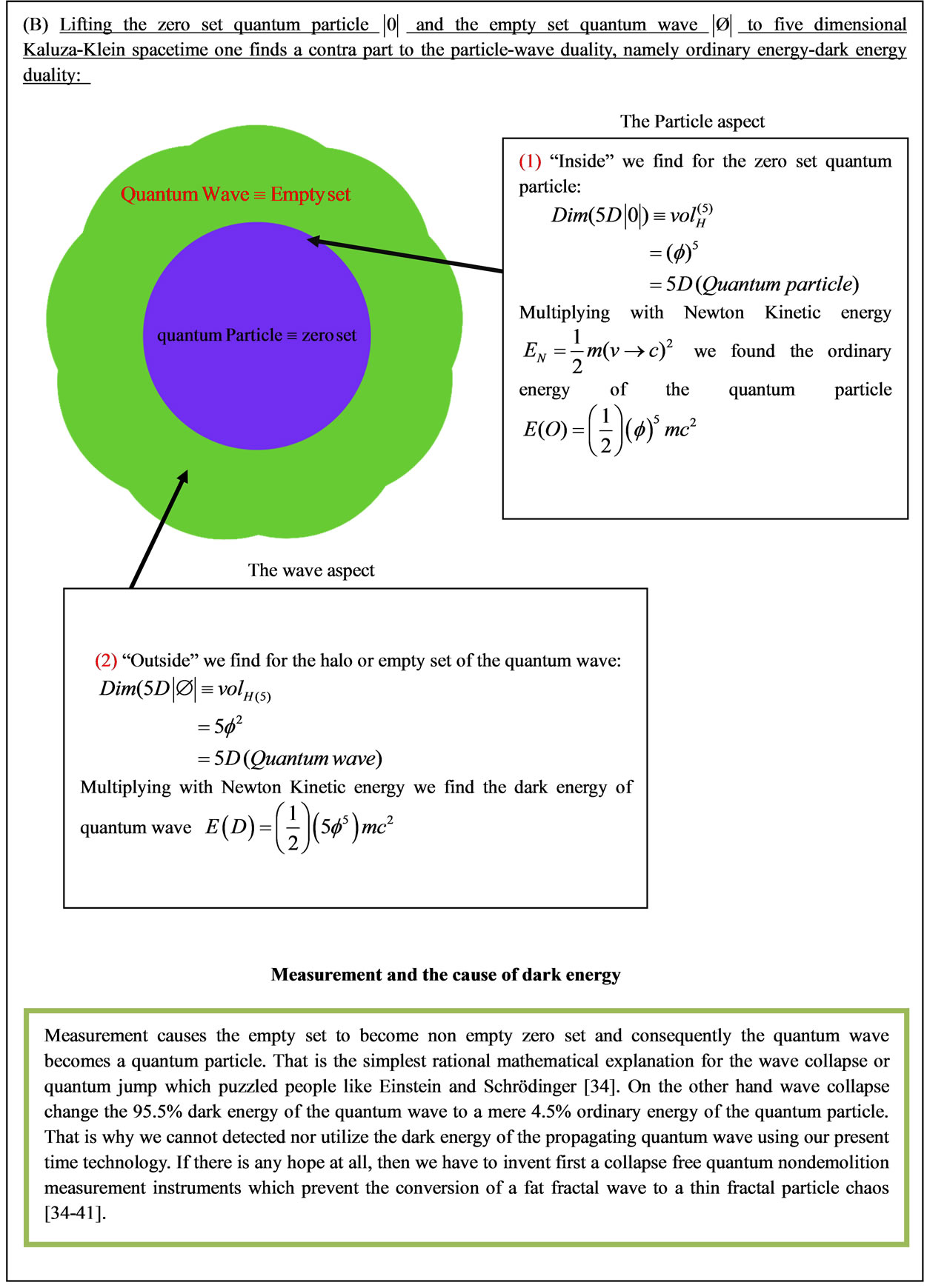
Figure 2. Quantum measurement and dark energy of the five dimensional Kaluza-Klein quantum wave.
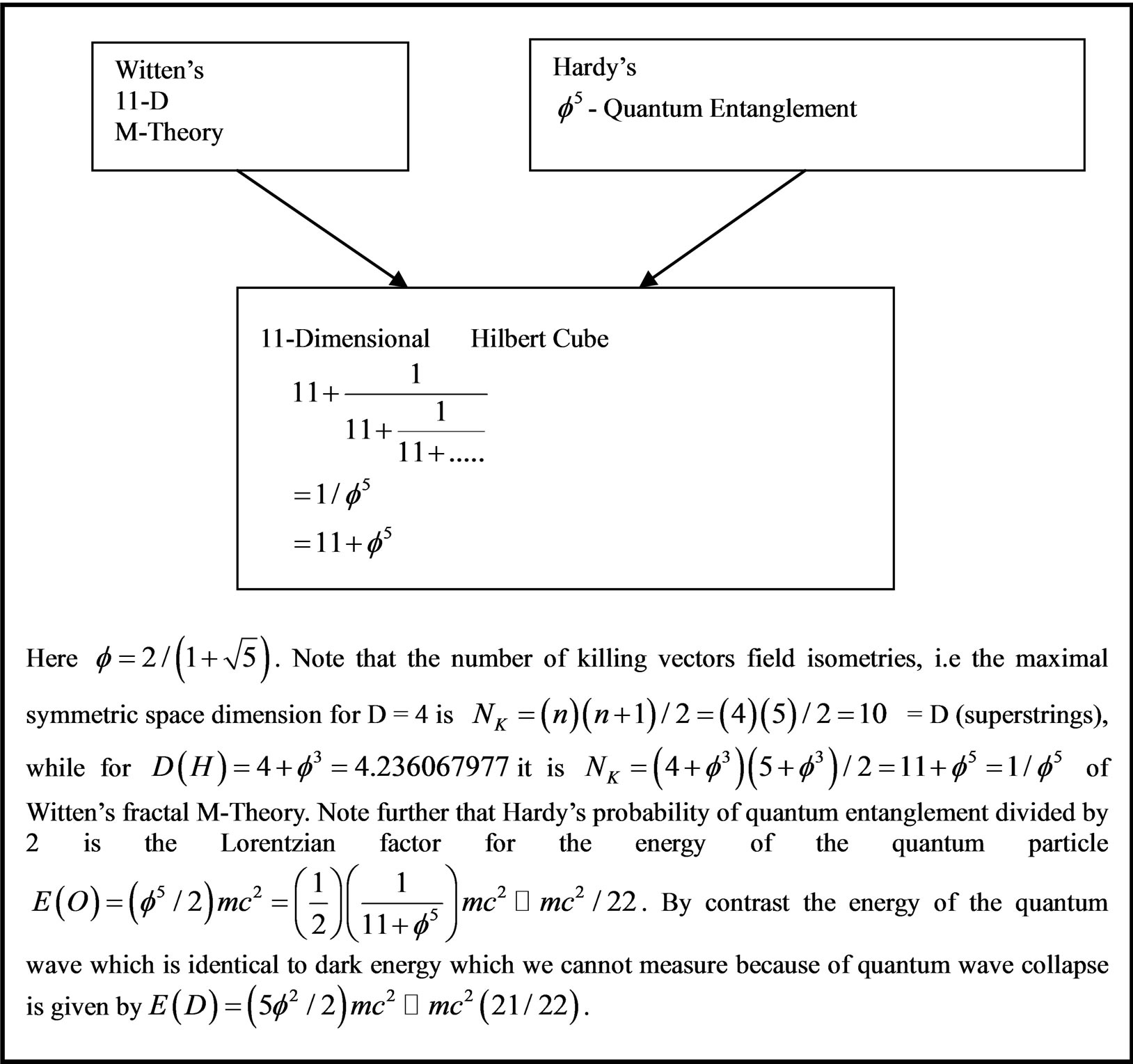
Figure 3. Combining Witten’s M-Theory and Hardy’s quantum entanglement to give a fractal M-Theory [23,24].
In the next section we review very briefly a few of the concepts and tools which we will need for revising Einstein’s equation of special relativity to a non-smooth spacetime geometry and elevating it to an equation of quantum gravity [17-35]. The intimate connection between non-classical physics and the source of this nonclassical behavior is essentially the fuzzy fractal geometry and fuzzy topology of spacetime. This is actually the most important point which we would like to underline in the present work [15-33]. The present resolution of the missing dark energy is only one important example of the power of the basic conclusion regarding the fractal non-classical nature of the fabric of four, five and eleven dimensional spacetime [2,3,22,25] (for more details see Figures 1-3). Even more profound than the above discussed result is the realization that dark energy is nothing but the energy of the quantum wave of the universe while ordinary energy is the energy of the quantum particle [35-39] (for elucidation see Figures 1, 2). On the other hand measurement collapses the Hawking-Hartle quantum wave of the cosmos which is the very reason why we cannot measure dark energy, unless we develop first some sophisticated quantum nondemolition measurement instruments [34]. Having said all that, it is still left open whether in view of KAM theorem the quantum wave and quantum spacetime is one and the same concept [39-54]. It is needless to say that dark energy is almost surely the driving force behind the increased rate of cosmic expansion and must be ascribed a physical reality however indirect. To enhance quick grasp of the plethora of the new ideas and results presented in this paper it is virtually summarized in 14 figures and charts in addition to the extensive commentaries there in.
2. General Background Information and Preliminary Remarks
As mentioned in the Introduction we will make here extensive use of the Penrose mathematical model for quasi crystals for which the Israeli engineering scientists Dan Shechtman was awarded the Nobel Prize in chemistry
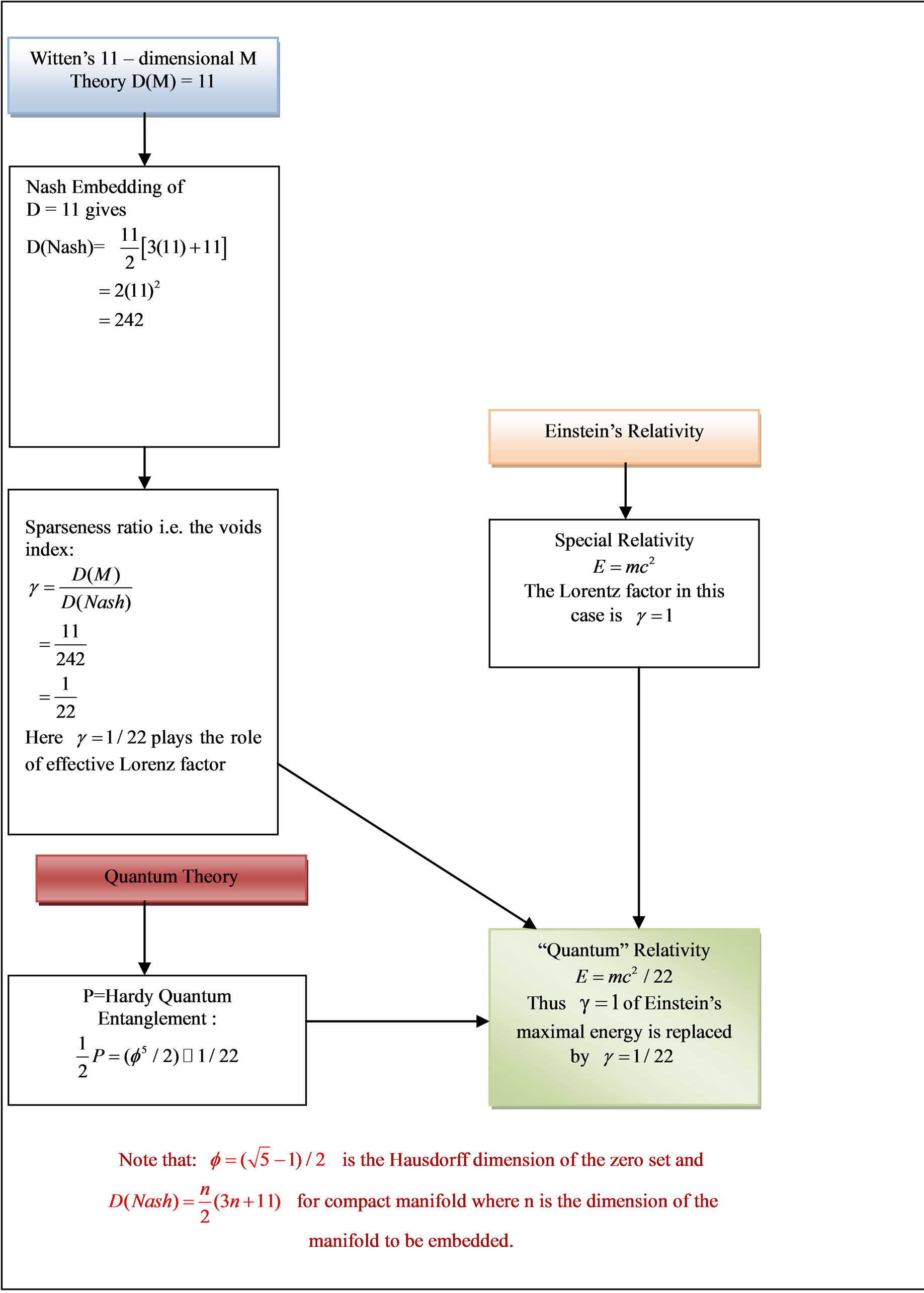
Figure 4. A flow chart starting from Nash global Euclidean embedding and Witten’s M-Theory explaining the logical connections and sequential deduction using Einstein relativity and leading to quantum relativity energy .
.

Figure 5. Finkelstein-like quantum relativity theory as an intersection of the three major fundamental theories of physics. Note that 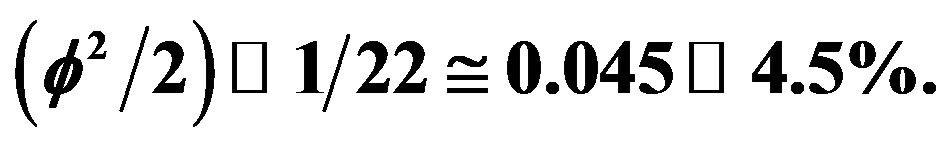 Consequently
Consequently  predicts 4.5% only of the energy which the classical equation of Einstein
predicts 4.5% only of the energy which the classical equation of Einstein  predicts. In other words,
predicts. In other words, 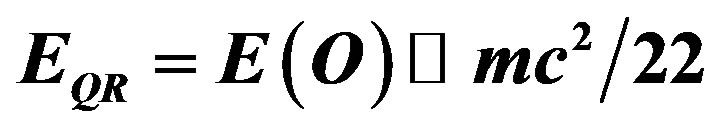 does not contradict the cosmological measurement but rather confirms the data of Refs. 17, 18 and 19. This is a clear cut resolution of the mystery of dark energy. It then turned out that ordinary energy is the energy of the quantum particle
does not contradict the cosmological measurement but rather confirms the data of Refs. 17, 18 and 19. This is a clear cut resolution of the mystery of dark energy. It then turned out that ordinary energy is the energy of the quantum particle  while dark energy is the energy of the quantum wave
while dark energy is the energy of the quantum wave . The sum is
. The sum is . Seen that way quantum spacetime and the quantum wave are different conceptions for one and the same thing. We cannot measure the energy of the quantum particle because measurement collapses the Hawking-Hartle quantum wave of the universe. In a single sentence, our theory is a based on D. Gross proposal to scale the Planck scale [58].
. Seen that way quantum spacetime and the quantum wave are different conceptions for one and the same thing. We cannot measure the energy of the quantum particle because measurement collapses the Hawking-Hartle quantum wave of the universe. In a single sentence, our theory is a based on D. Gross proposal to scale the Planck scale [58].
(2011) [4,9]. This is the well known Penrose-fractal tiling which is a two dimensional projection of a KaluzaKlein like five dimensional space [4,9]. Seen from the view point of noncommutative geometry, Penrose tiling is a quotient space and consequently a geometric realization of an essentially quantum structure. However one of the most important attributes of quantum particles is spin and Penrose tiling [4,9] does not have the extra spin 1/2 dimension of Fermions [4]. Taking 4 dimensions to be the natural habitat for Boson, we recognize the need for one more degree of freedom or 5 dimensions like in Kaluza-Klein theory to accommodate spin half. For a super symmetric Penrose space we must therefore combine two spaces together and find the corresponding quasi periodic structure [4,9]. As for the two and three Stein spaces, we know that the sum of all the 17 dimensions of these spaces comes up to exactly [16]
 (1)
(1)
where E12 is a conjectured exceptional Lie symmetry group [13]. There are deep reasons for this sum to be equal to 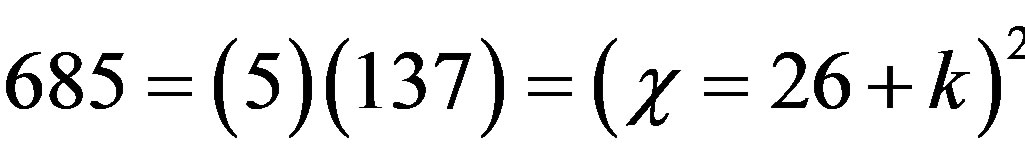 where
where 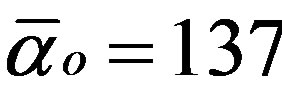 is the exact integer value for the inverse electromagnetic
is the exact integer value for the inverse electromagnetic

Figure 6. The Bi-Algebra and Bi-dimension theory of the 5-D quantum particle and the 5-D quantum wave [43] and corresponding energy using Newton’s kinetic energy as a template.

Figure 7. Classification and dictionary of normalized energies.

Figure 8. Overview on Weyl-Nottale scaling.
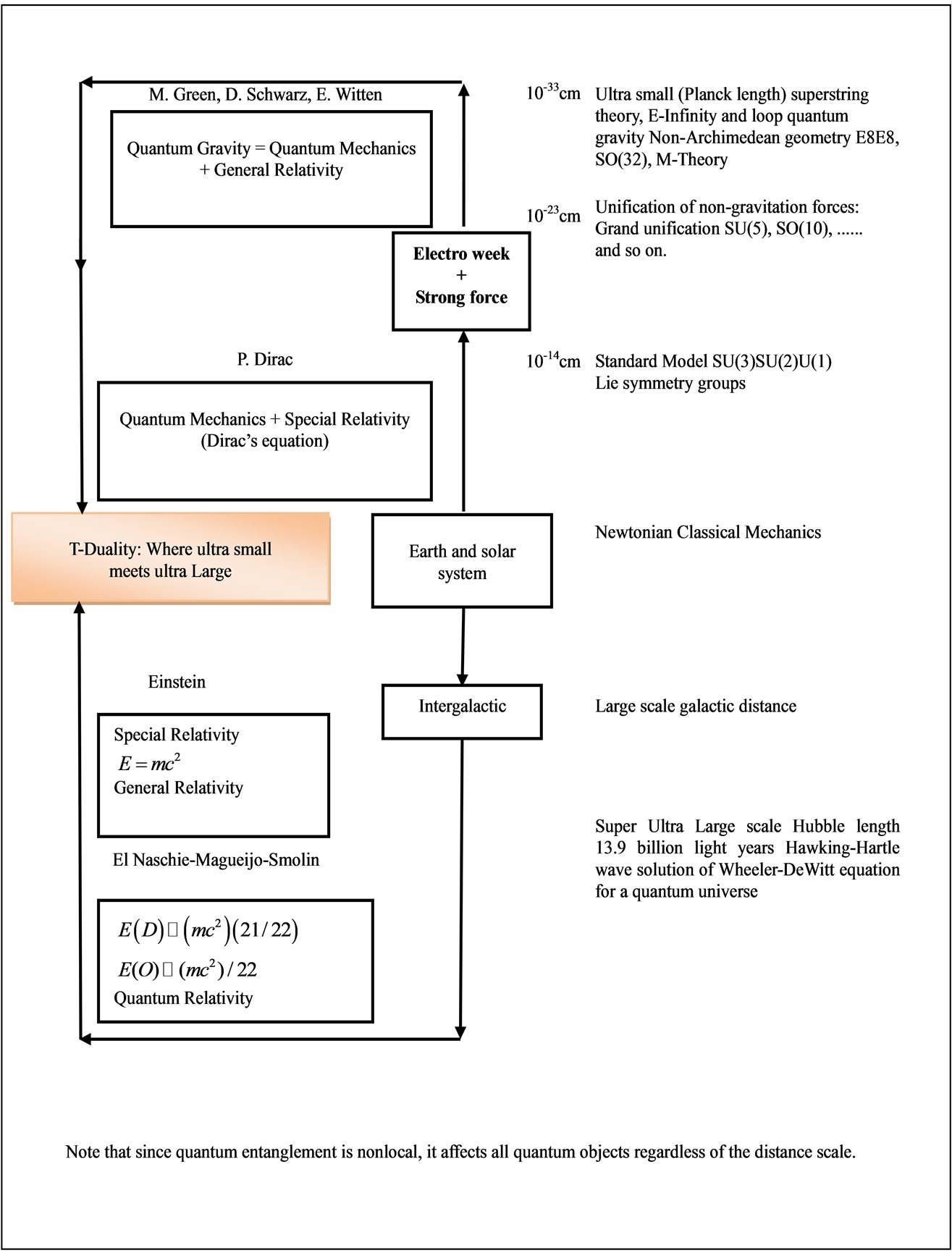
Figure 9. The length scales and ranges of validity for relativity and quantum mechanics.
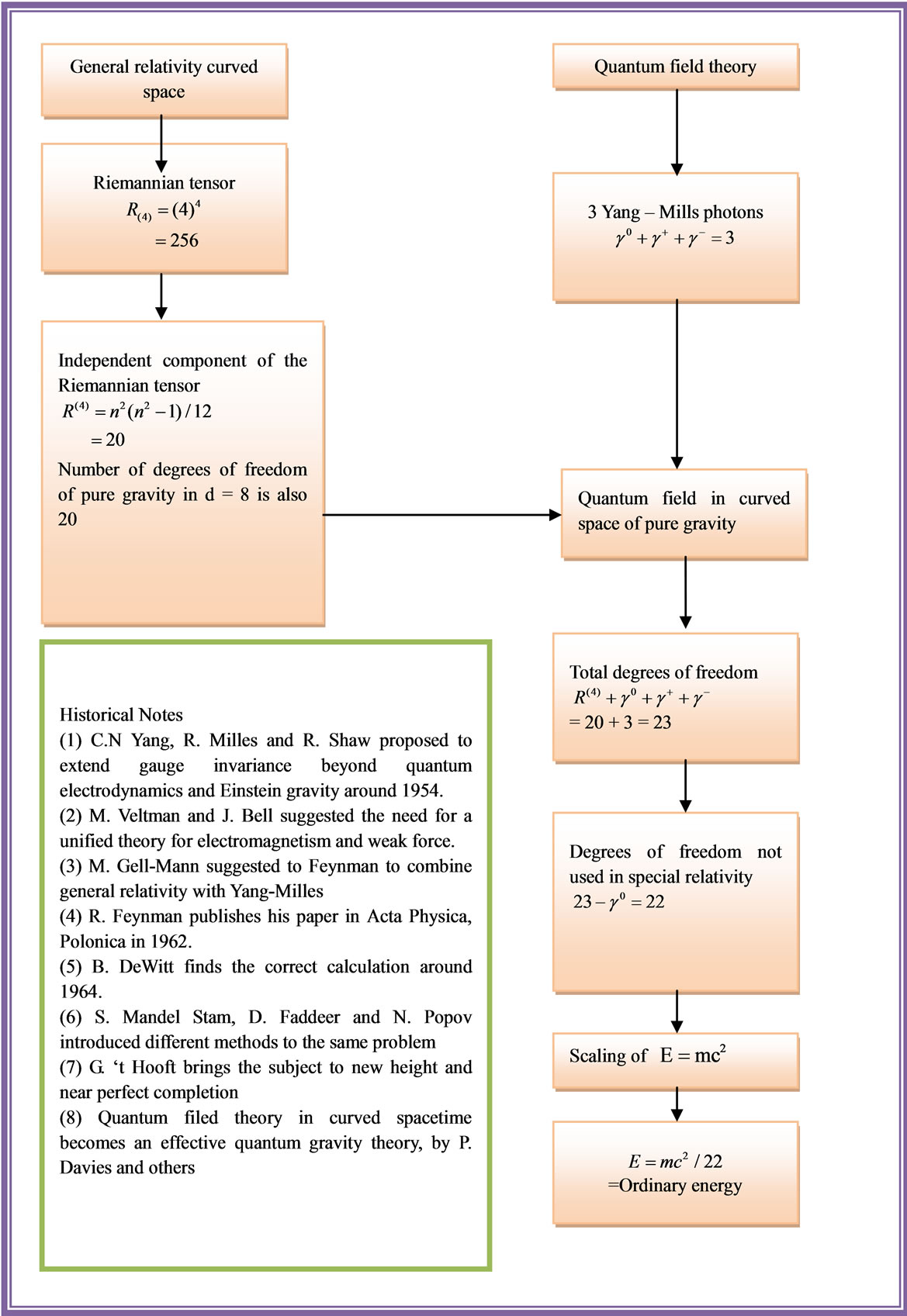
Figure 10. Overview on Deriving  from quantum field theory in curved spacetime or combining Yang-Mills theory with Einstein’s general relativity following R. Feynman’s and DeWitt’s work.
from quantum field theory in curved spacetime or combining Yang-Mills theory with Einstein’s general relativity following R. Feynman’s and DeWitt’s work.
 (a)
(a)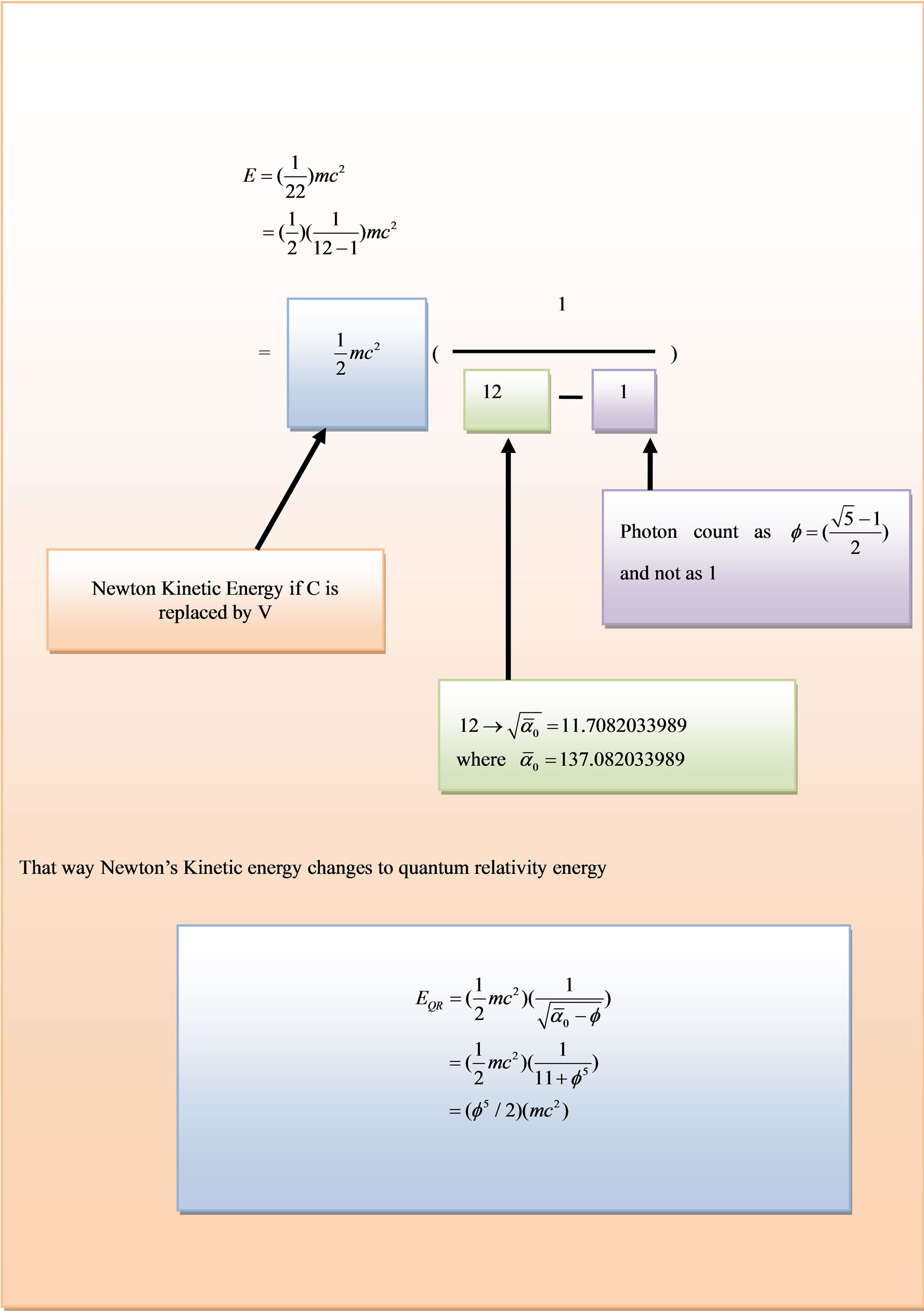 (b)
(b)
Figure 11. (a) Overview on applying fractal (fuzzy) logic in quantum gravity [41]; (b) Overview high energy physics counting versus fractal counting leading to simple formula for quantum relativity.

Figure 12. Overview on main conclusions.
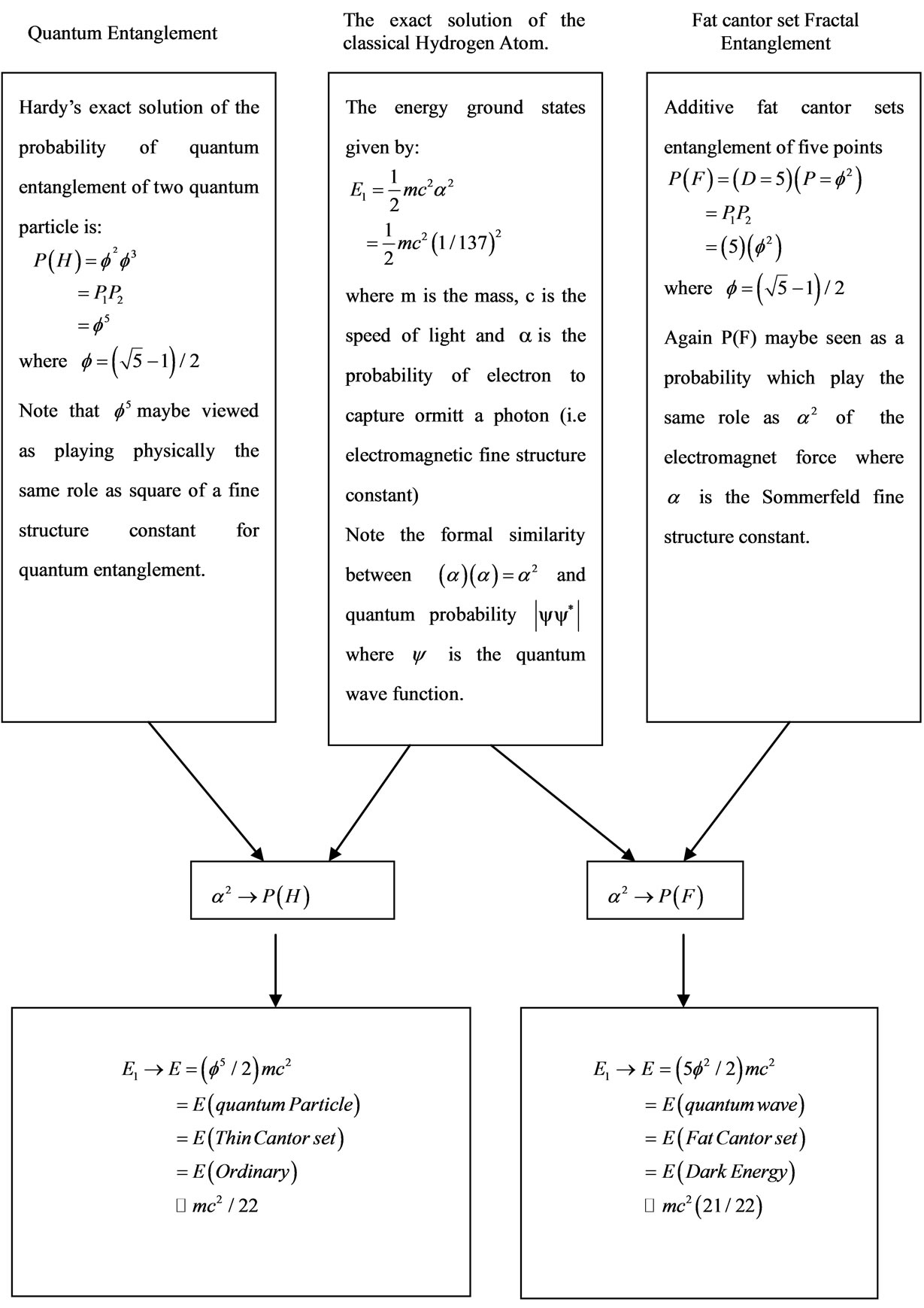
Figure 13. Deriving ordinary energy and dark energy from the ground state energy of the Hydrogen Atom.

Figure 14. Curvature-anti-curvature in material space: A simple demonstration indicating an analogy to negative curvature and antigravity. By squeezing a real material space in the form of a long cylindrical tube in the middle the circular cross section becomes oval shaped. However, this is only in the middle but as we move towards the far ends of the cylinder, the oval cross section rotates and takes a perpendicular position at the edge (see explanation in the main text, paragraph 7).
fine structure constant, 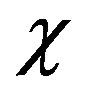 is the curvature of spacetime [28],
is the curvature of spacetime [28],  ,
,  is the probability of Hardy’s quantum entanglement [27] and
is the probability of Hardy’s quantum entanglement [27] and  [16]. Remarkably the sum of the dimensions of all the eight exceptional Lie groups of the E-line display a related behavior because [16-19]
[16]. Remarkably the sum of the dimensions of all the eight exceptional Lie groups of the E-line display a related behavior because [16-19]
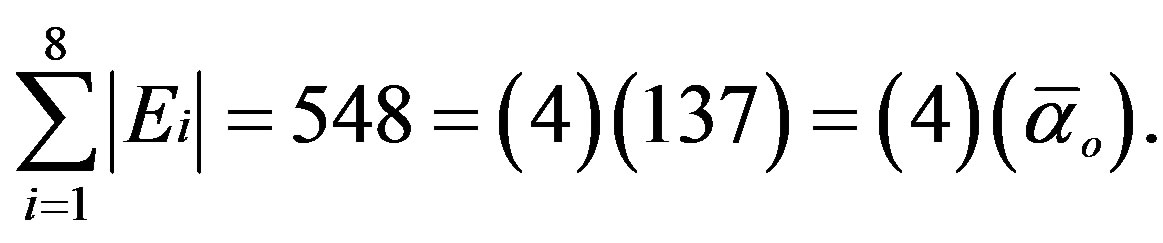 (2)
(2)
In fact we have
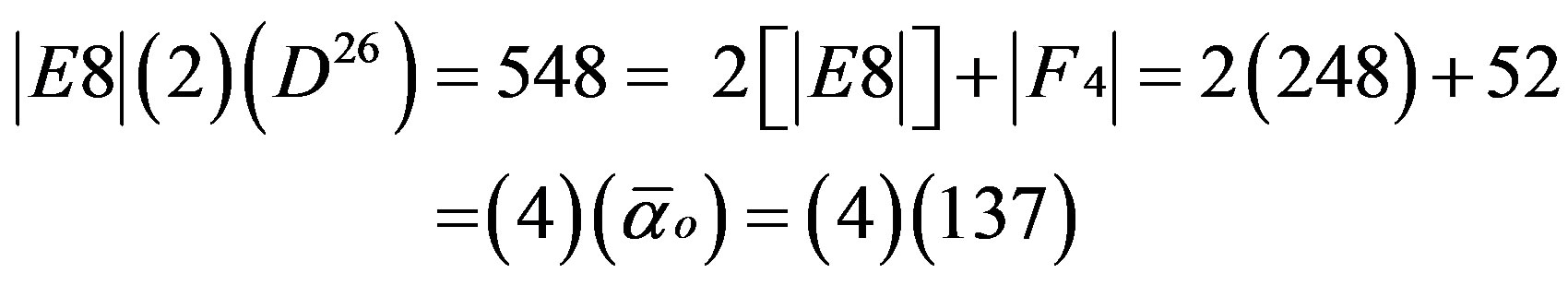 (3)
(3)
where 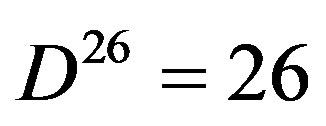 and
and  is also one of the original five exceptional Lie symmetry groups,
is also one of the original five exceptional Lie symmetry groups, 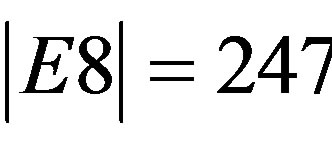 ,
,  ,
, 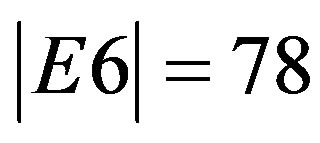 ,
, 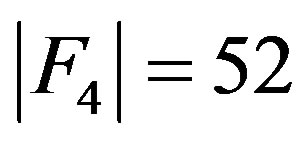 and
and 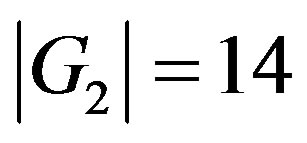 as well as the rest of the E-line
as well as the rest of the E-line 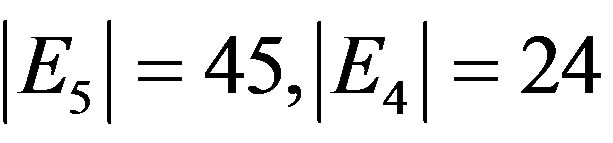 and
and  which were used extensively by the first author to develop high energy physics beyond the standard model [16-19]. In anticipation of discussing the role of symmetry groups in explaining the negative curvature effect of dark energy, we should mention a few further facts. First the sum of the dimension of the groups E8 to E5 is 504 which is equal to the corresponding particle like states of E8E8 Heterotic superstrings while adding E4 leads to 528 dimensions which is the maximal number of isometries or killing vector fields of Witten-Duff five Branes in the D = 11 model 18,50]. We note in anticipation of some later derivation that the sum of the dimension of the 17 Stein spaces is equal to the square of the curvature of our Cantorian fractal spacetime [28]. In other words the energy stored in this spacetime is [28]
which were used extensively by the first author to develop high energy physics beyond the standard model [16-19]. In anticipation of discussing the role of symmetry groups in explaining the negative curvature effect of dark energy, we should mention a few further facts. First the sum of the dimension of the groups E8 to E5 is 504 which is equal to the corresponding particle like states of E8E8 Heterotic superstrings while adding E4 leads to 528 dimensions which is the maximal number of isometries or killing vector fields of Witten-Duff five Branes in the D = 11 model 18,50]. We note in anticipation of some later derivation that the sum of the dimension of the 17 Stein spaces is equal to the square of the curvature of our Cantorian fractal spacetime [28]. In other words the energy stored in this spacetime is [28]
 (4)
(4)
3. Mathematical Background Information and Preliminary Considerations
Since KAM theorem of nonlinear dynamics and fractal weight and counting are important tools in the present analysis and to make the work reasonably self contained, we give first a brief summary of these subjects.
3.1. KAM Theorem [42] and Cantorian Foliation of Energy—General Remarks
Let us consider first a fairly familiar fact of Measure Theory [43] applied to certain number theoretical aspects of rational and irrational numbers on the real number line. It is well known that although both sets of numbers are dense, the former is zero measure while the latter has positive measure. The situation is precisely analogous to the Hamiltonian nonlinear dynamics energy Manifold and its Cantorian foliation of a two degree of freedom system with non-degenerating varying frequency ratio [42]. There we have the non-resonant tori possessing positive Lebesgue measure like the empty set modeling the quantum wave while the resonant tori have zero measure like the zero set modeling the quantum particle. Both sets are interwoven as in the famous KAM picture of nonlinear dynamic and Hamiltonian deterministic chaos. Furthermore we know that slight perturbation will destroy some of the non-resonant tori. That means empty set changes into zero set or in quantum physics terminology wave to particles i.e. we have state vector reduction or wave collapse due to perturbation caused for instance by measurement. The above brings immediately to mind the classical example used in nonlinear dynamical systems to illustrate the quintessence of KAM and the golden mean resonance ratio as the last bastion of stability before global chaos set on, namely “thick” fate Cantor set of positive Lebesgue measure changes into thin random Cantorian chaos [18,43-46]. Here we have again connection to E-Infinity and high energy physics because the building blocks of Cantorian spacetime are random cantor sets with a golden mean Hausdorff dimension [25]. This we consider further next.
3.2. Measure Theory, Thin and Thick Cantor Sets
The coastline of Norway is easily computed from a global map. However if we have to take into account all the fjords and those branching from them including every dent and stone then the task is almost impossible. This is the main point in fractals applied to nature namely to tame divisions using a theory with the obvious natural name: Measure Theory. Thus loosely speaking a set is a zero measure in certain spaces when it is not impossible but infinitely unlikely to find at random a point in this space.
Let us start by consider some illustrative simple examples and regard a unit interval [0, 1] i.e. all real numbers between zero and 1 including the end points. If we take a segment 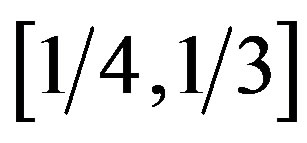 then the Lebesgue measure is
then the Lebesgue measure is  which is a positive number. This is a positive Lebesgue measure. Let us consider infinitely many points
which is a positive number. This is a positive Lebesgue measure. Let us consider infinitely many points . This is a zero Lebesgue measure] because a set of points, no matter how many are of total length zero. Cantor middle third set deterministic or random have also a zero measure. However the complement of these set, has a positive Lebesgue measure equal to one. In Ref. [47] we considered previously wild topology and fate fractals in high energy physics. In both cases of the above mentioned sets it was shown in the reference mentioned that we have Cantor dust of a Cantor set but in the case of positive Lebesgue measure we have thicker dust.
. This is a zero Lebesgue measure] because a set of points, no matter how many are of total length zero. Cantor middle third set deterministic or random have also a zero measure. However the complement of these set, has a positive Lebesgue measure equal to one. In Ref. [47] we considered previously wild topology and fate fractals in high energy physics. In both cases of the above mentioned sets it was shown in the reference mentioned that we have Cantor dust of a Cantor set but in the case of positive Lebesgue measure we have thicker dust.
3.3. The Thin Cantor Set Quantum Particle and the Thick Cantor Set Quantum Wave
It is easily shown that thin random Cantorian fractal dust are zero sets with topological dimension zero and Hausdorff dimension 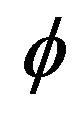 exactly as the zero set of the quantum particle, while the complementary thick Cantor set is the empty set with topological dimension minus one and Hausdorff dimension
exactly as the zero set of the quantum particle, while the complementary thick Cantor set is the empty set with topological dimension minus one and Hausdorff dimension 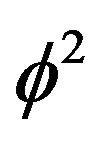 like the quantum wave. Thus the measure of both sets added together is
like the quantum wave. Thus the measure of both sets added together is  and similarly for the dimensions we have
and similarly for the dimensions we have  leading to something resembling classical Newtonian particle. From the above it may be tempting to ponder considering the quantum wave to be nothing but the quantum manifestation of the geometry and topology of a multifractal spacetime geometrical quasi manifold. Seen that way the Hawking-Hartle quantum wave of the cosmos as well as Feynmann’s nondifferentiable propagator would be more or less a different name for what is essentially the same mathematical construction with the same physical effect which could be labeled more direct as simply quantum spacetime [44-46].
leading to something resembling classical Newtonian particle. From the above it may be tempting to ponder considering the quantum wave to be nothing but the quantum manifestation of the geometry and topology of a multifractal spacetime geometrical quasi manifold. Seen that way the Hawking-Hartle quantum wave of the cosmos as well as Feynmann’s nondifferentiable propagator would be more or less a different name for what is essentially the same mathematical construction with the same physical effect which could be labeled more direct as simply quantum spacetime [44-46].
3.4. Fractal “Fuzzy” Counting of Fuzzy Fractal Logic
An essential part of understanding the set theoretical approach to quantum mechanics of the present derivation of dark energy from the quantum mechanics of the hydrogen atom (see Figure 13) is fractal counting. The theory of fractal logic [41] is a very recent offspring of Lotfi Zadeh’s fuzzy sets and fuzzy logic [48] which was outlined in few relatively recent publications [14,22,25,45]. In the context of high energy particle physics, the theory makes profound and unbelievable claims which are nevertheless accurate and leads to results in full agreement with experiments and the essence of many, if not all, theoretically generally accepted mathematical models of high energy physics [33].
To see this one should carefully ponder the implication of the following at first sight completely outrageous statement.
Assertions:
The twelve massless gauge bosons of the standard model (MS) where 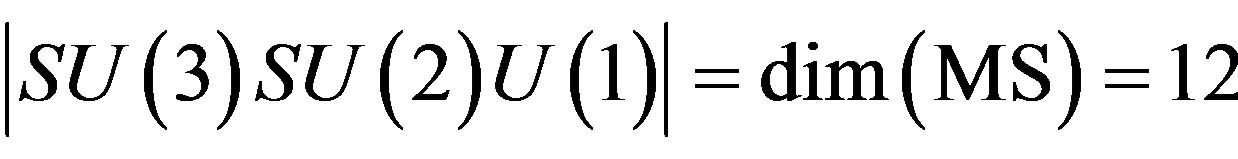 are in fact 14 particles and include the Higgs bosons as well as the graviton although the fuzzy fractal number of these particles is neither 12 nor of course 14 but 11.7082032... or more accurately
are in fact 14 particles and include the Higgs bosons as well as the graviton although the fuzzy fractal number of these particles is neither 12 nor of course 14 but 11.7082032... or more accurately

where  is the E-Infinity theoretical value of the inverse electromagnetic fine structure constant [22,25].
is the E-Infinity theoretical value of the inverse electromagnetic fine structure constant [22,25].
In other words the standard model is complete and includes the Higgs as well as the graviton. The only confusing thing is that the number of the Higgs and graviton elementary particle is not an integer as the experimenters expect. It is a fractally weighted number and very difficult to identify in the laboratory. This fact is the real reason for the difficulties associated with accurately identifying certain particles unambiguously in experimental facilities. We are expecting to count a number of particles as we count marbles or coins. However this is only a highly idealized picture familiar to us from our Newtonian classical every day surrounding only. The real high energy quantum physics picture is fuzzy fractal and counting particles should also be “accurately” fractal no matter how this statement may seem contradictory. In fact this is the essence of the lesson taught to us by Zadah fuzzy logic [48]. Therefore we should count high energy messenger particle as follows:
a) Strong Interaction:
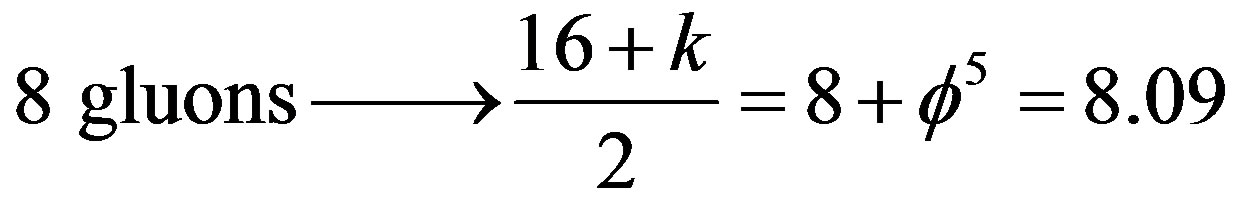
b) Week Force:
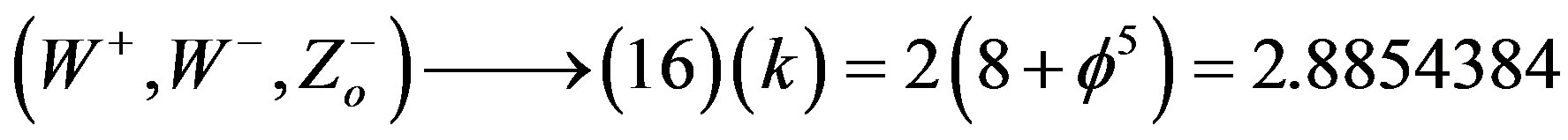
c) Electromagnetism:
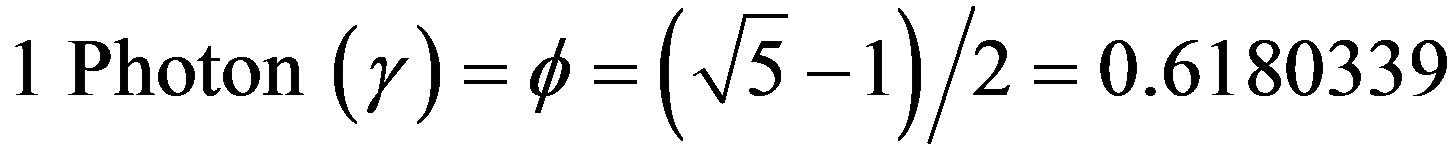
Mass and Gravity:

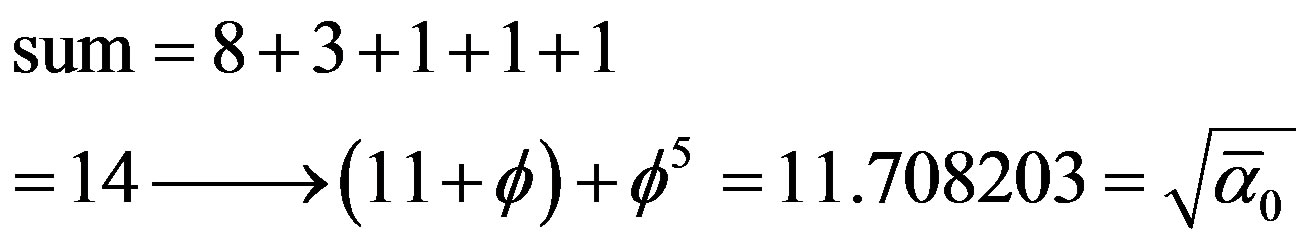
Thus we have:
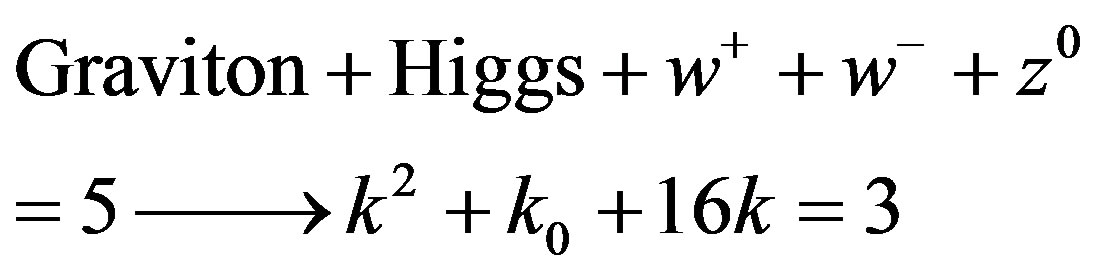
In other words the integer fundamental equation:
 Gravity + Electromagnetism + Holographic boundary
Gravity + Electromagnetism + Holographic boundary
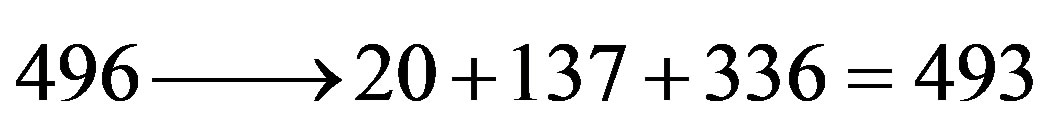 where E8 is the largest exceptional Lie symmetry group of the E-Line becomes an equality when adding electroweak + Higgs + Gravity and finding the exact equation of the conservation of the dimensions and isometries of the involved lie symmetry groups and degrees of freedom:
where E8 is the largest exceptional Lie symmetry group of the E-Line becomes an equality when adding electroweak + Higgs + Gravity and finding the exact equation of the conservation of the dimensions and isometries of the involved lie symmetry groups and degrees of freedom:
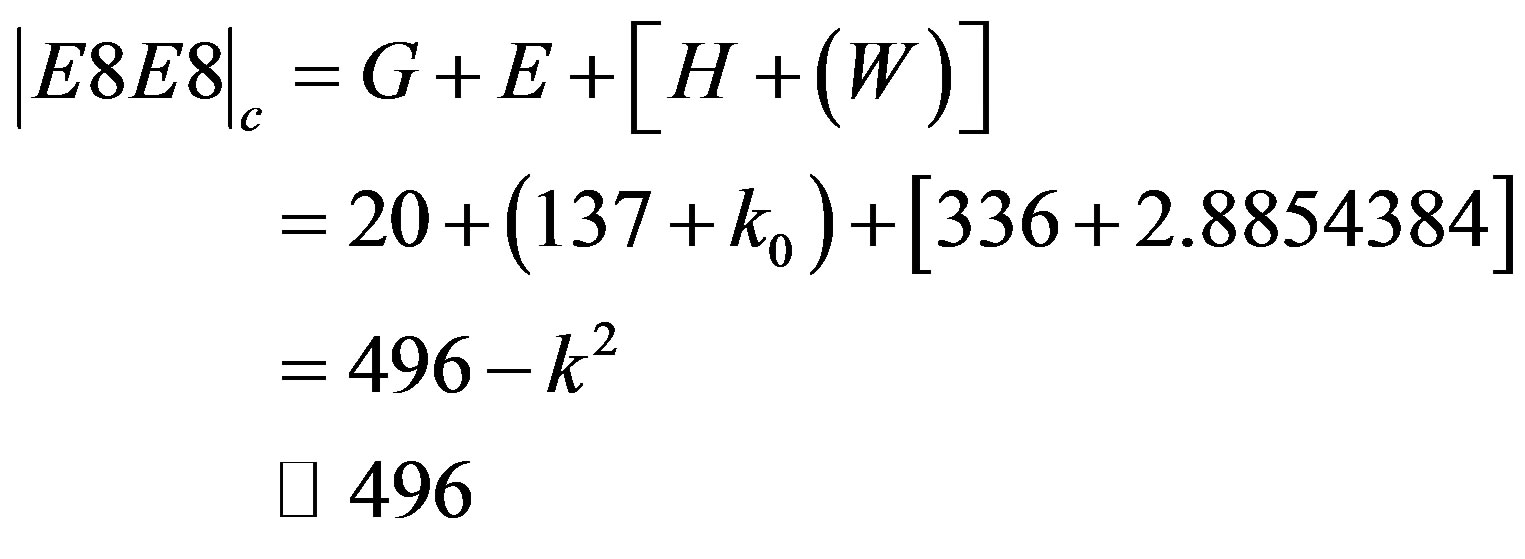
wher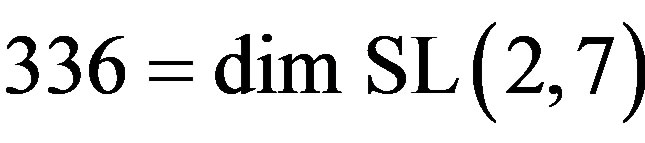 ,
, 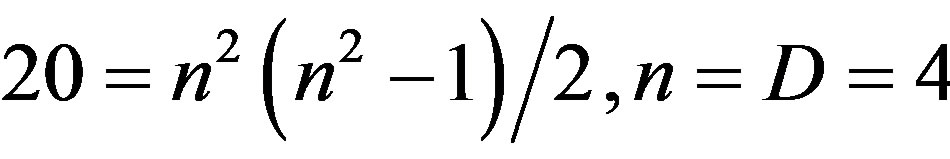 ,
,

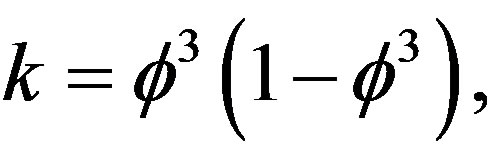 . Here G is gravity, E is electromagnetism, H is the holographic boundary, i.e. particle physics and W is the electroweak given by SU(2) in the integer approximation [22,25].
. Here G is gravity, E is electromagnetism, H is the holographic boundary, i.e. particle physics and W is the electroweak given by SU(2) in the integer approximation [22,25].
4. The Super Symmetric Penrose Quasi Crystal Tiling Space
The simplest fractal-like higher dimensional space one can think of is the Hilbert cube [20]. The dimension of this cube coincides with the expectation value of the Hausdorff dimension of the core of what is in the meantime fairly familiar E-infinity Cantorian fractal spacetime and is given by [20,21]

This infinite continued fraction is easily summed up to [20,21]
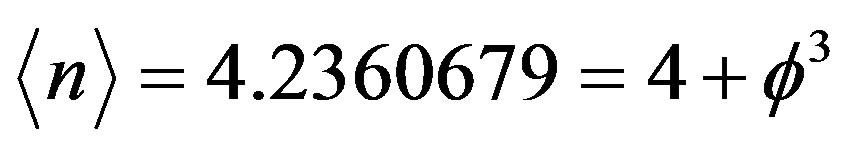
where .
.
The above result corresponds to a Menger-Urysohn topological dimension of exactly nt = 4. It is easy to see that from
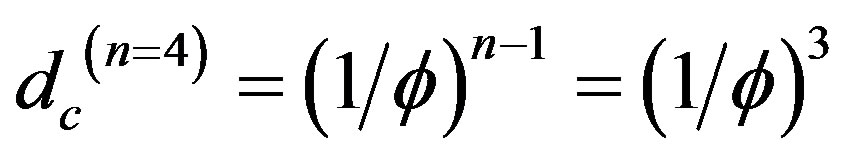 and find
and find
 .
.
Consequently to give the core of this space the additional spin 1/2 degree of freedom we need to consider a Hilbert cube with [22]

Now the space which unifies Boson and Fermions must be the intersection of both spaces which means
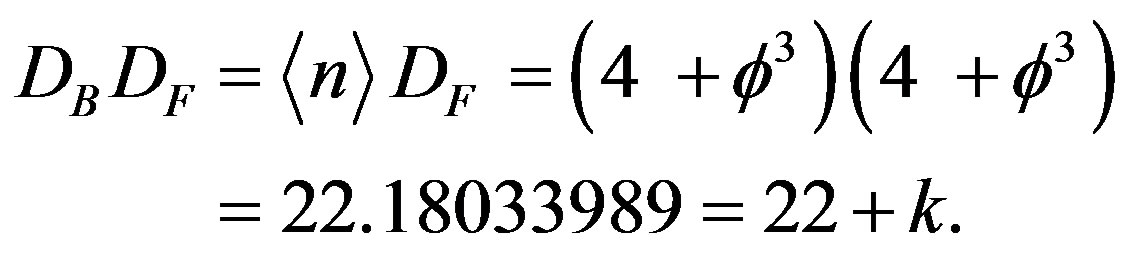
We know that the isomorphic length, i.e. the radius of the hyperbolic quotient space of the classical Penrose tiling is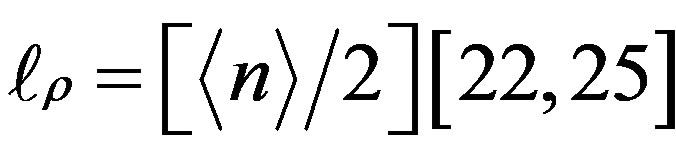 . By analogy for
. By analogy for  the isomorphic length is
the isomorphic length is . It is then trivial to see that the radius of the new super symmetric Penrose space is given by the following isomorphic length [23, 24]
. It is then trivial to see that the radius of the new super symmetric Penrose space is given by the following isomorphic length [23, 24]
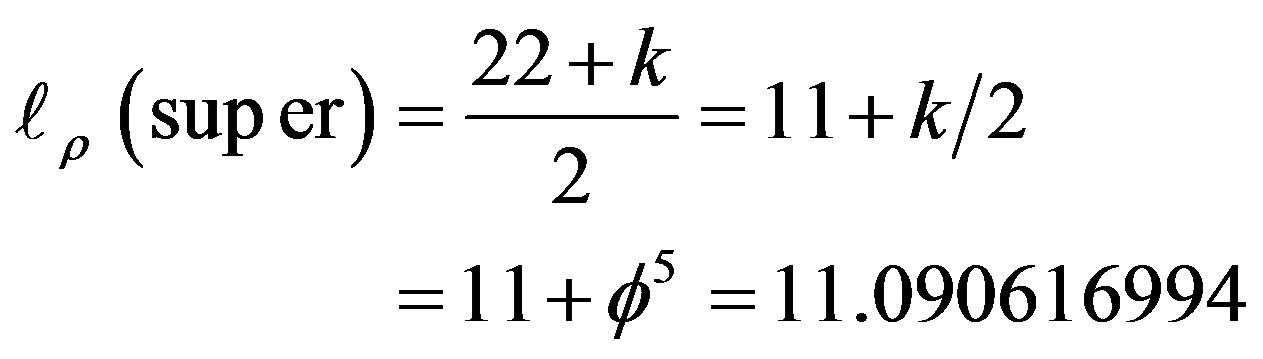
Noting that Witten’s almost all embracing M-theory is eleven dimensional, then we must conclude that similar to our 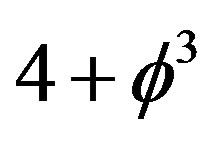 dimensional Hilbert cube, we now have an eleven dimensional Hilbert cube or equivalently a fractal Witten-like M-theory with a quasi Hausdorff dimension (see Figure 3) [23,24]
dimensional Hilbert cube, we now have an eleven dimensional Hilbert cube or equivalently a fractal Witten-like M-theory with a quasi Hausdorff dimension (see Figure 3) [23,24]

This is an 11 dimensional theory corrected transfinitely by adding 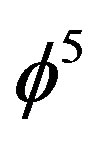 Hardy’s quantum probability of entanglement to it. We thus have this most important result, namely that the intrinsic or counterfactual quantum probability [25-27] of a fractal point in super symmetric M-theory space is clearly the inverse of
Hardy’s quantum probability of entanglement to it. We thus have this most important result, namely that the intrinsic or counterfactual quantum probability [25-27] of a fractal point in super symmetric M-theory space is clearly the inverse of  which is exactly because
which is exactly because  , i.e. Hardy’s generic entanglement [26,27]. Second, the super symmetric Penrose quasi crystal is essentially a fractal version of Witten’s M-theory and the corresponding fractal dimension is
, i.e. Hardy’s generic entanglement [26,27]. Second, the super symmetric Penrose quasi crystal is essentially a fractal version of Witten’s M-theory and the corresponding fractal dimension is 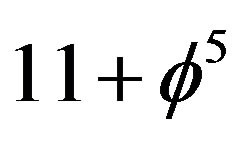 [19,26,27]. We conclude further that the corresponding Menger-Urysohn topological dimension is n = 6 like the dimension of Calabi-Yau manifold because (see Figure 3) [25]
[19,26,27]. We conclude further that the corresponding Menger-Urysohn topological dimension is n = 6 like the dimension of Calabi-Yau manifold because (see Figure 3) [25]
 .
.
In other words the fractal M-theory space has exactly 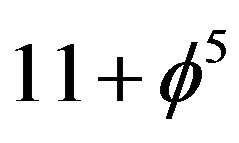 compactified dimensions, i.e.
compactified dimensions, i.e. 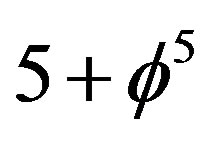 are totally curled up, presumably in the form of a fractal version of Witten’s 5D Brane [4,19]. Our super symmetric Penrose space turned out to be truly fundamental and represents de facto a version of Witten’s 5D Brane in eleven dimensions which we mentioned in paragraph two of the present work [19]. Since this Witten model is maximally symmetric and the associated number of killing vector fields (see Figure 3) is 528 given
are totally curled up, presumably in the form of a fractal version of Witten’s 5D Brane [4,19]. Our super symmetric Penrose space turned out to be truly fundamental and represents de facto a version of Witten’s 5D Brane in eleven dimensions which we mentioned in paragraph two of the present work [19]. Since this Witten model is maximally symmetric and the associated number of killing vector fields (see Figure 3) is 528 given
 then our fractal version will inherit much of this maximal symmetry and the fractional number of killing vector fields becomes
then our fractal version will inherit much of this maximal symmetry and the fractional number of killing vector fields becomes
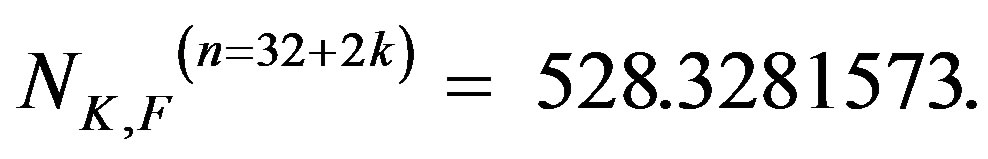
We conjecture that this space is at a minimum homomorphic to the Poincaré dodecahedral [31,32] proposed by Jean-Pierre Luminet for a wrap around well proportioned spacetime manifold [6,8]. It is relevant to note that 528 is also the sum of the dimension of the exceptional Lie groups

as discussed in Ref. [25]. Furthermore we see here a vital connection to anti-curvature of dark energy for the following: It is the different classical symmetry considerations which reduce the 256 components of the Riemannian tensor in D = 4 to only 20 independent components. However it is the ratio 504/528 = (21)/22 which decides upon dark energy where N(32) = 528 is maximally symmetric space and 504 is the sum of the dimensions of E8, E7, E6 and E5 as mentioned earlier on.
5. Cosmic Crystallography and the Heterotic String Connection
It is truly a remarkable mathematical fact that there exists only 17 wallpaper (Islamic) symmetry groups in two dimensions. In addition only 17 two and three Stein spaces [7,16] exist with a sum of dimension 686 which we mentioned earlier on. In flat Euclidean 3 dimensional space there are only 17 distinct multiply connected spaces [6]. The two and three Stein spaces are the most interesting for us here however because of the following interesting question which arises when we look at Stein space as a crystalographic group projected onto two dimensions [7,16]. If the dimensions of the 17 Stein spaces are assigned to the 17 wallpaper groups, then knowing that the number of 3 dimensional crystalographic groups is 230 and that only  of these groups correspond to the 17 two dimensional groups, then we can ask what is the dimension of these 219 groups corresponding to our 686 total dimensions discussed earlier [7,16]. Including as usual in our theory certain simplectic transfinite corrections [15] related as will be explained shortly to the Hardy quantum entanglement effects [26, 27], we can write
of these groups correspond to the 17 two dimensional groups, then we can ask what is the dimension of these 219 groups corresponding to our 686 total dimensions discussed earlier [7,16]. Including as usual in our theory certain simplectic transfinite corrections [15] related as will be explained shortly to the Hardy quantum entanglement effects [26, 27], we can write

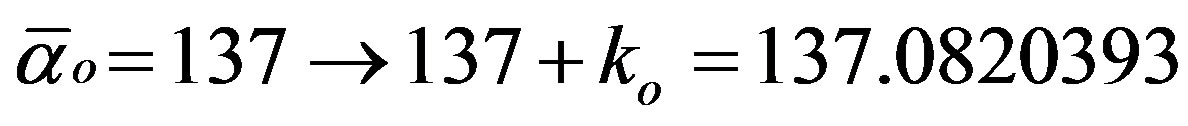
and
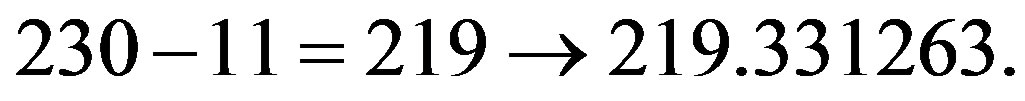
That way one finds the total dimensions corresponding to 686 to be [7]
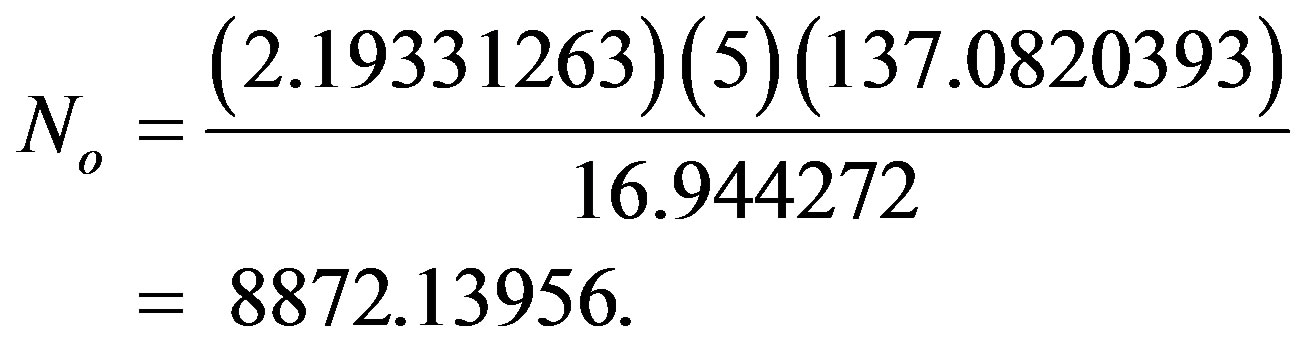
This is exactly the transfinitely exact corrected number of the first massless level of elementary particle-like states in the Heterotic spectrum. The sharp (non-fuzzy) ordinary value is of course the well known (336)(24) = 8064 [25]. Our value here corresponds to (336 + 16k) (24 + 2 + k). In other words, our value corrects 24 to almost 26 and 336 to approximately 339. It is possible then to analyze the missing dark energy using either the Bulk of 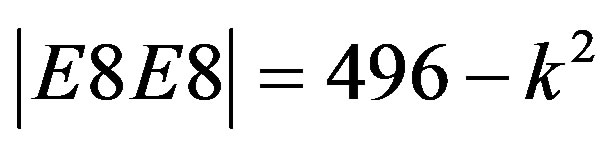 or the holographic boundary
or the holographic boundary , where
, where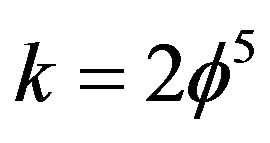 . The result will remain the same [17]. The objective of this section was merely to show that our result is deeply woven into Heterotic string theory and not only crystallography. In fact Euclidean embedding according to Nash formula [28,29] also plays a major role in taming “wild” symmetry groups. For instance the dimension 7 is the Nash embedding of one dimensional object and leads to
. The result will remain the same [17]. The objective of this section was merely to show that our result is deeply woven into Heterotic string theory and not only crystallography. In fact Euclidean embedding according to Nash formula [28,29] also plays a major role in taming “wild” symmetry groups. For instance the dimension 7 is the Nash embedding of one dimensional object and leads to 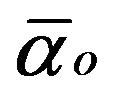 while two dimensional objects give Nash dimension 17 and leads to
while two dimensional objects give Nash dimension 17 and leads to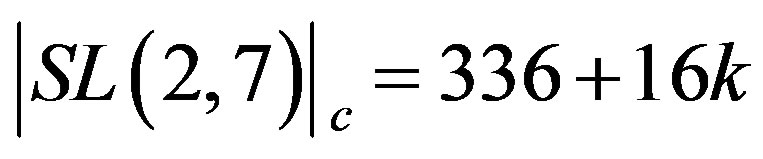 . For the sake of completion we briefly give this analysis starting from Nash’s formula for compact manifolds [25,28,29]
. For the sake of completion we briefly give this analysis starting from Nash’s formula for compact manifolds [25,28,29]

For n = 1 and n = 2 e find that

and

respectively. Taking 20 copies of the quantum and transfinite corrections of 7 one finds [25]
 and for the Immirzi entanglement
and for the Immirzi entanglement  one find:
one find:

respectively as should be.
In the next section we will be demonstrating how the preceding result can be used in a way relative at least in spirit to Hawking no boundary proposal and the quantum wave of the universe by summing over all compact matrices [36,37]. We also note that Euclidean embedding plays an important role via Campbell’s local embedding theorem in the work of P. Wesson on five dimensional physics [43].
6. Weeks Minimal Hyperbolic Space and the Density or Ordinary Energy and Dark Energy
Hyperbolic manifolds cannot have arbitrary small volumes [6,8]. Their volume is quantized so to speak with a minimum depending on shape. In 3D we have such a situation in knot theory for instance of what is called hyperbolic volume discussed in previous publications [20]. In connection with the work on Poincaré dodecahedron, J. Weeks found what at present is still the smallest volume of a hyperbolic space, namely [6]
V(weeks) = 0.94272 R3.
This space has 44 elements namely 26 points like the Bosonic strings and 18 faces. If our actual spacetime were made of such volumes, then it is tempting to conjecture that these volumes are the geometrical quanta of a unit which represents in part a screened volume so that only  remains. The energy inside is not there because the inside is a spacetime void. Consequently about 5.728% of the presumed energy of such a space will be a sort of dark energy [1]. We appreciate that it may be a far shot but more accurate consideration will show that the idea is not that much out and may come nearer to reality than meets the eyes. To outline the idea let us start by remembering that the average Hausdorff dimensions are in an infinite dimensional space [22,25] is
remains. The energy inside is not there because the inside is a spacetime void. Consequently about 5.728% of the presumed energy of such a space will be a sort of dark energy [1]. We appreciate that it may be a far shot but more accurate consideration will show that the idea is not that much out and may come nearer to reality than meets the eyes. To outline the idea let us start by remembering that the average Hausdorff dimensions are in an infinite dimensional space [22,25] is . Similarly in negative four dimensions the average dimension is
. Similarly in negative four dimensions the average dimension is . Being a Hausdorff dimension it is half way between being dimensions and being a volume [22,25]. Remembering that
. Being a Hausdorff dimension it is half way between being dimensions and being a volume [22,25]. Remembering that 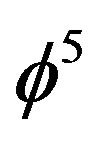 s also Hardy’s generic quantum entanglement [26,27], then one could view
s also Hardy’s generic quantum entanglement [26,27], then one could view  s being a sort of average minimal quasi “volume” or building block of spacetime. Recalling that the volume of a unit ball is
s being a sort of average minimal quasi “volume” or building block of spacetime. Recalling that the volume of a unit ball is 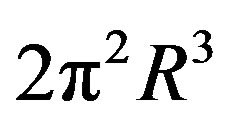 then setting
then setting  the
the  of classical geometry could be set directly in relation to
of classical geometry could be set directly in relation to 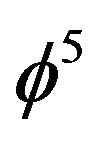 in Cantorian geometry. Consequently
in Cantorian geometry. Consequently  is the classical value of
is the classical value of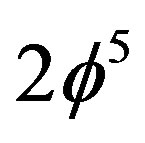 . This
. This 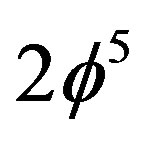 is nothing else but
is nothing else but
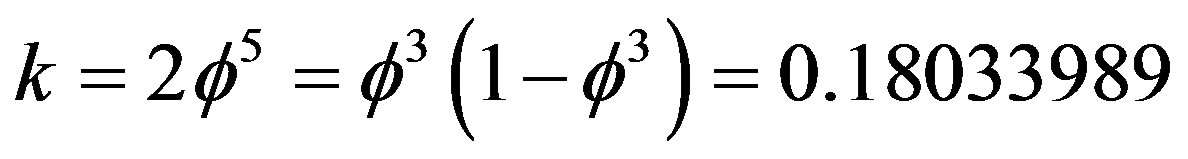
[22,25] which we meet continuously when adding or subtracting transfinite corrections in our theory to ensure symplecticity, i.e. area preservation and global harmony of the principal of maximal numerical harmony [33]. Now if we continue 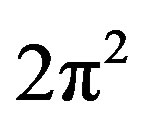 transfinitely then we can write [33]
transfinitely then we can write [33]
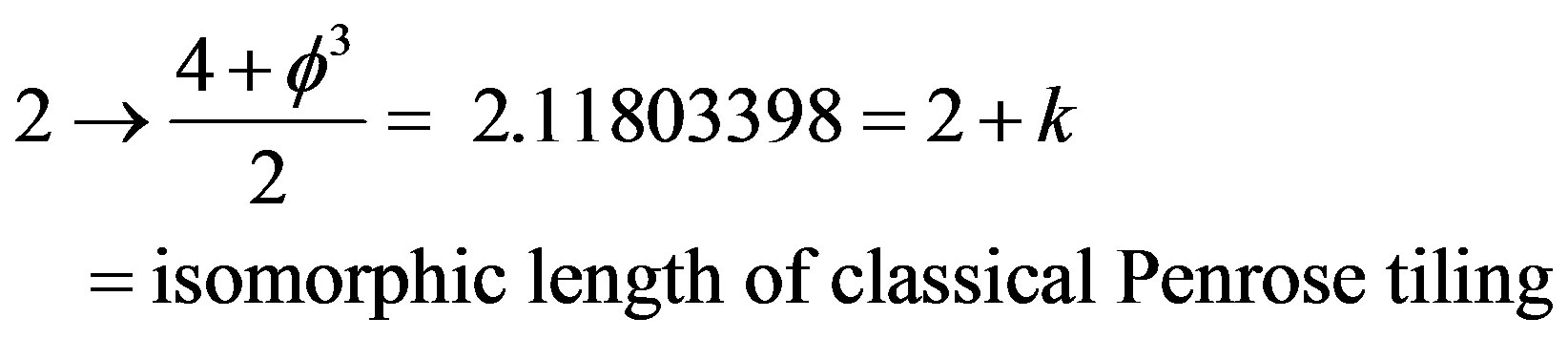
and
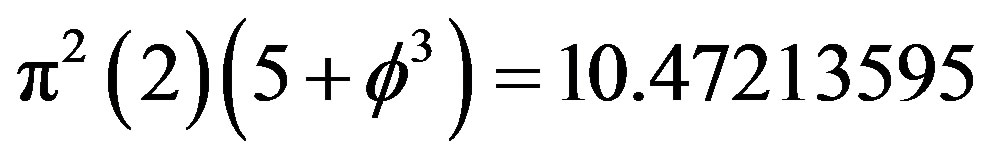 .
.
Thus we have [33]
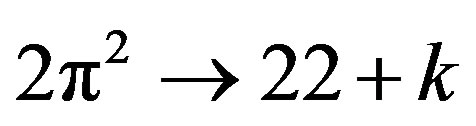 .
.
Measuring  in terms of our k minimal units we find
in terms of our k minimal units we find
 .
.
Thus our minimal Cantorian volume is about 123 times smaller than the classical volume. On the other hand we see that
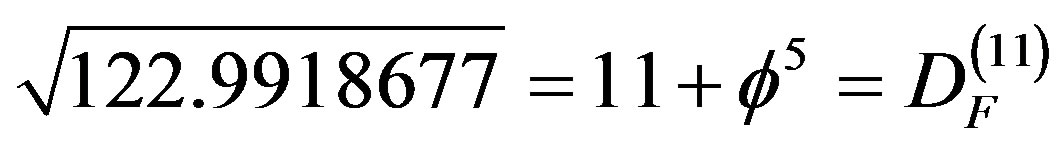
which is the dimension of fractal M-theory and therefore it is clear now that [22,25]

From these elementary considerations it is obvious that the total energy predicted in a classically correct way must be reduced by a factor equal to  i.e. a factor of
i.e. a factor of . The classical energy of Newton
. The classical energy of Newton

should therefore be changed according to
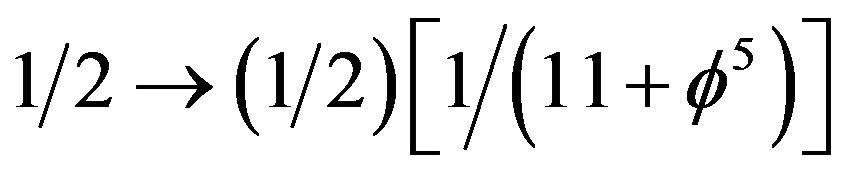
and
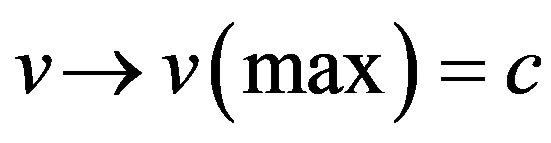
when we move towards the speed of light. At this speed spacetime becomes a Cantorian fractal and this is actually evident from the existence of effects such as the Rindler Wedge and Unruh temperature [17-29]. It is quite instructive at this point to look carefully at Equations (6) and (10) of relativistic Kinetic energy T as given by Rindler on page 112 in [35]. This equation reads . Setting
. Setting  qual to that of our quantum relativity energy of the quantum particle equation namely
qual to that of our quantum relativity energy of the quantum particle equation namely 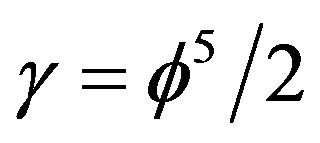 e see immediately that T become a negative energy value namely
e see immediately that T become a negative energy value namely
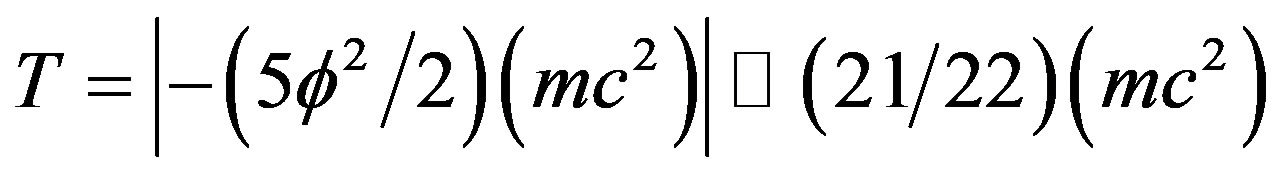
hich is identical to the kinetic quantum energy of the quantum wave. Note now the factor given by the ratio 21/22 which is exactly that obtained from considering the E-line of the exceptional Lie groups given in paragraph 4. This is also clearly the negative dark energy of the propagating quantum wave which on measurement transmute into quantum a potential ordinary energy
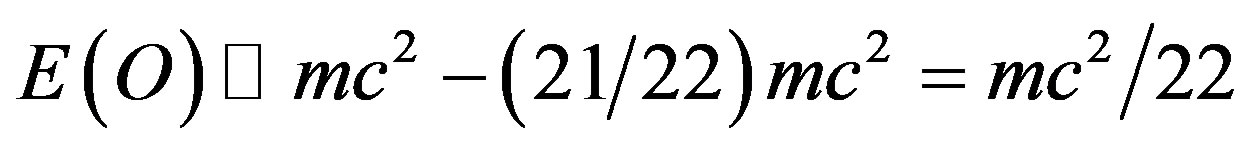
which we measure and we may be justified in liking it to the position energy of classical mechanics only in this case thw word position is not a sharp concept [45-47]. We conjecture that unless quantum wave nondemolition measurement instruments are used in future cosmological measurement it will not be possible to detect dark energy directly because of the quantum wave collapse [34,36,39]. The proceeding analysis also illustrates the paramount role played by hyperbolic geometry in fractal-quantum gravity and quantum relativity [40]. It is of paramount importance that our 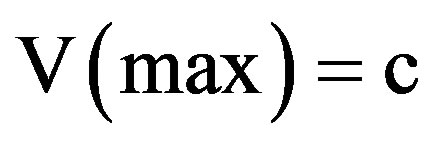 is not a constant but a sharp expectation average of a speed varying between zero and infinity because of the multi fractal nature of our Cantorian empty set micro spacetime [21,38]. Our theory may therefore be considered a varying speed of light theory like that of Moffat and Magueijo [53,54].
is not a constant but a sharp expectation average of a speed varying between zero and infinity because of the multi fractal nature of our Cantorian empty set micro spacetime [21,38]. Our theory may therefore be considered a varying speed of light theory like that of Moffat and Magueijo [53,54].
We note on passing that as the total energy stored in spacetime is proportional to the square of the curvature of spacetime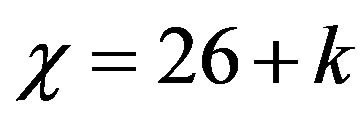 , i.e.
, i.e.
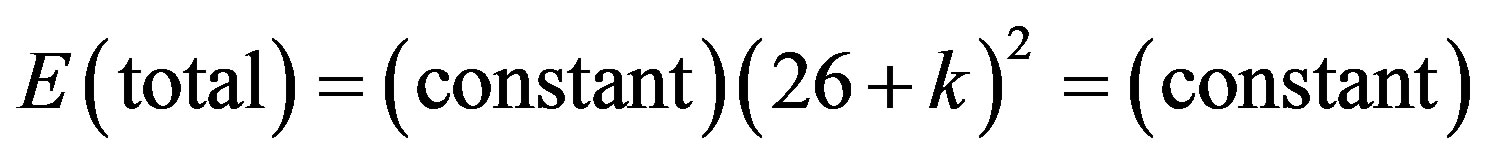 (685.4)the dark energy of the cosmos is proportional to the square of the curvature of the compactified dimension
(685.4)the dark energy of the cosmos is proportional to the square of the curvature of the compactified dimension , i.e.
, i.e.

where E8 is the largest exceptional Lie symmetry group [28].
7. The Reason for the Missing Dark Energy
From the preceding discussion we saw how a quasi crystal space, basically a super symmetric form of Penrose fractal tiling leads to the conclusion that Einstein’s energy-mass equation must be scaled down by a factor of 1/22 in order to encompass quantum mechanics via quantum entanglement. This is basically a reduction proportional to the dark dimensions of Bosonic strings. We mean that on the other hand a theory of almost everything [4] says that we need 26 spacetime dimensions [4]. However Einstein’s equation is based upon only 4 dimensions [4]. It follows then on the other hand that 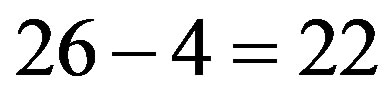 dimensions are hidden away and we intuittively see that these dimensions swallow energy which we call dark energy. Consequently we can call these dimensions dark dimensions. Now this could all be seen as a consequence of the quasi crystal fractal spacetime effect which causes the exact generic quantum entanglement to be
dimensions are hidden away and we intuittively see that these dimensions swallow energy which we call dark energy. Consequently we can call these dimensions dark dimensions. Now this could all be seen as a consequence of the quasi crystal fractal spacetime effect which causes the exact generic quantum entanglement to be 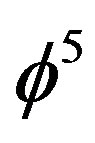 [26,27]. The factor in Einstein’s equation which should replace
[26,27]. The factor in Einstein’s equation which should replace 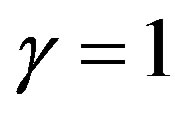 is
is . This is exactly what we found here in different ways and it could be shown that an appropriate Lorentzian transformation coupled to light cone quantization [30] will lead to the same result. In fact the fractal
. This is exactly what we found here in different ways and it could be shown that an appropriate Lorentzian transformation coupled to light cone quantization [30] will lead to the same result. In fact the fractal  dimensional version of Witten’s M-theory also leads to identical results as can easily be demonstrated and as is obvious from
dimensional version of Witten’s M-theory also leads to identical results as can easily be demonstrated and as is obvious from . Having said all of the above we must not overlook a second even deeper and more profound explanation for why we cannot detect dark energy. To put in a nutshell, dark energy is the energy of the quantum wave as modeled by the empty set in D = 5 while ordinary energy is the energy if the quantum particle modeled by the zero set in D = 5 Kaluza-Klein spacetime [26,27,38,39]. Consequently wave collapse on measurement will reduce an empty set quantum wave to a non-empty zero set quantum particle which means the total energy of the particle-wave is reduced to the energy of the particle only which amounts to only 4.5% of what is expected based on relativity theory. In Figure 4 we give an overview of the relation between Nash Embedding fractal M-Theory and the quantum relativity energy formula. In Figure 7 we give yet another overview on the normalized energy of different fundamental theories including loop quantum gravity and Unruh temperature. We also stress yet again the role of antigravity of the compactified hidden dimensions of spacetime in causing the increased rate of cosmic expansion as illustrated by the toy model of Figure 14.
. Having said all of the above we must not overlook a second even deeper and more profound explanation for why we cannot detect dark energy. To put in a nutshell, dark energy is the energy of the quantum wave as modeled by the empty set in D = 5 while ordinary energy is the energy if the quantum particle modeled by the zero set in D = 5 Kaluza-Klein spacetime [26,27,38,39]. Consequently wave collapse on measurement will reduce an empty set quantum wave to a non-empty zero set quantum particle which means the total energy of the particle-wave is reduced to the energy of the particle only which amounts to only 4.5% of what is expected based on relativity theory. In Figure 4 we give an overview of the relation between Nash Embedding fractal M-Theory and the quantum relativity energy formula. In Figure 7 we give yet another overview on the normalized energy of different fundamental theories including loop quantum gravity and Unruh temperature. We also stress yet again the role of antigravity of the compactified hidden dimensions of spacetime in causing the increased rate of cosmic expansion as illustrated by the toy model of Figure 14.
8. Regge-Like Quantum-Relativity Triangulation—Scaling the Planck Scale [58]
It is quite obvious that our minimal areas related to Hausdorff-like zero set quantum particle and the empty set spacetime or quantum wave [44-46] could be given a Regge calculus [4] “outlook” to say the least. At a minimum this geometrical tiling of the energy scape is quite instructive and can help deepen the understanding of the methodology leading to the two main energy density formulas obtained for ordinary and dark energy E(O) and E(D) respectively. The main point is that we could “Regge tile” our space in the case of the ordinary energy reduction factor 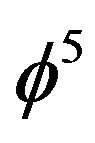 by either a rectangular area elements
by either a rectangular area elements  and then use as an “energy template” the Newton kinetic energy
and then use as an “energy template” the Newton kinetic energy 
and obtain our by now familiar quantum relativity formula for ordinary energy, namely:
 .
.
Alternatively and more in keeping with the conventional Regge triangulation as well as the geometry of our Klein modular holographic boundary to use triangular tiling so that the minimal area is
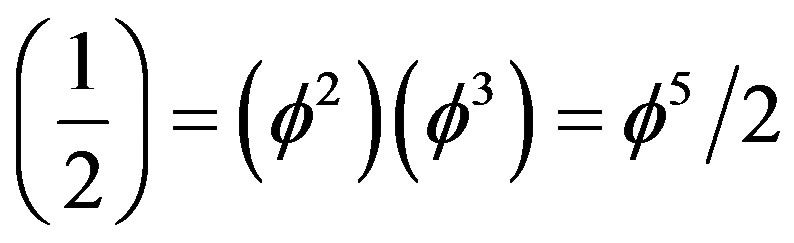 i.e. half of the quantum probability of Hardy’s entanglement. However in this case we must use Einstein’s energy as a “template” and find that:
i.e. half of the quantum probability of Hardy’s entanglement. However in this case we must use Einstein’s energy as a “template” and find that:
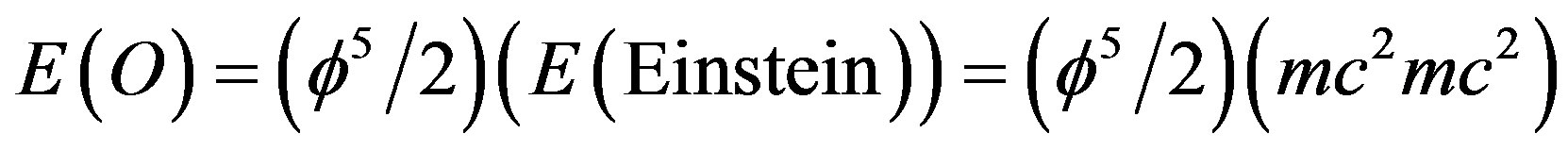 .
.
The same thing may be applied to the dark energy factor 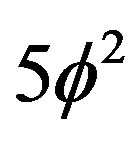 which is made of two parts, namely
which is made of two parts, namely 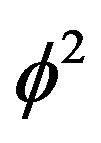 epresenting the square of the topological velocity of light
epresenting the square of the topological velocity of light  and 5 which is the topological Kaluza-Klein mass
and 5 which is the topological Kaluza-Klein mass . Again using Newton’s energy as a template one finds
. Again using Newton’s energy as a template one finds
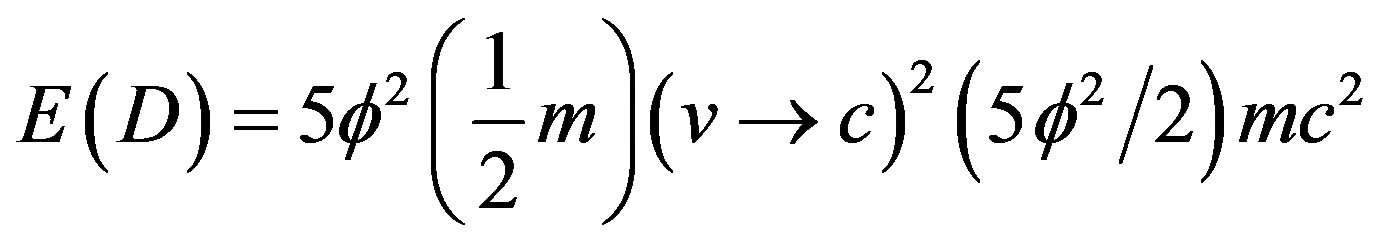 .
.
Alternatively we could use the Regge triangular minimal area, namely 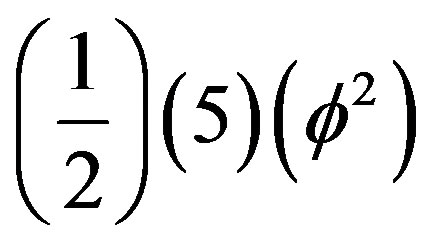 and Einstein energy as a template and obtain [54-57]
and Einstein energy as a template and obtain [54-57]
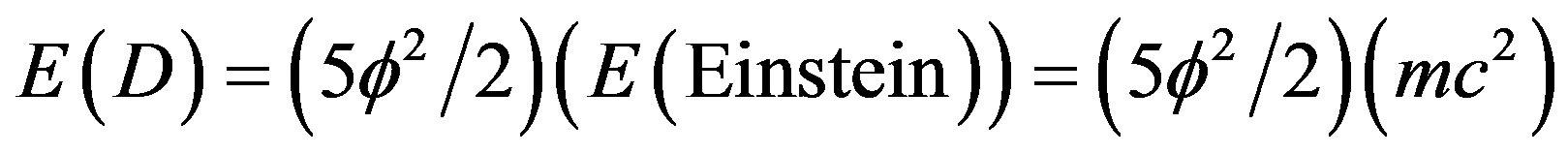 .
.
That way we see that our transfinite set theoretical approach to quantum physics, via scaling the Planck scale following D. Gross [58] is anchored in topology and we could use Newton or Einstein energy because they only connect the super structure to the topological foundation [44-46].
9. A Clopen on Average Flat Real Spacetime
Let us first recall that both of Einstein’s theories, the special and the general are based upon one isotropic spacetime geometry. By contrast and as reasoned on many previous occasions the very constancy of the measured speed of light being a constant expectation value implies the fundamental postulates of all fractal Cantorian spacetime theories that spacetime is only on the average quasi isotropic. In fact the Einstein spacetime isotropy was questioned long ago notably by Edward but also by others [4]. Now let us consider the Friedmann-RobertsonWalker metric [4]. With the conventional notation this is
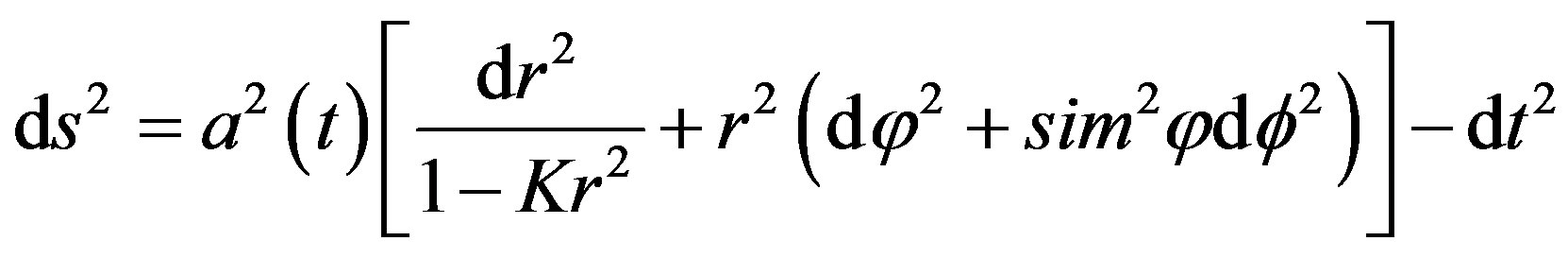
where K describes the spatial part of the geometry of spacetime. It is advantageous for understanding K to write ds2 in the following form
 .
.
That way we find that the following three values of :
:
1) 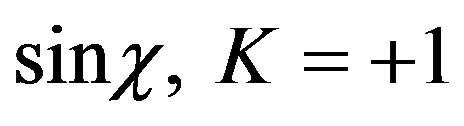 closed spacetime 2)
closed spacetime 2) 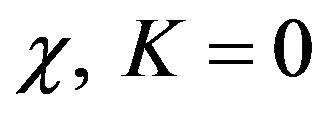 flat spacetime 3)
flat spacetime 3) 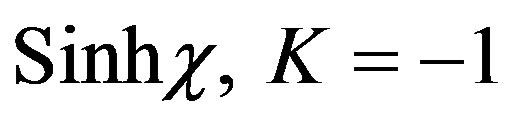 open universe.
open universe.
Note that the open universe involves a hyperbolic function and thus hyperbolic geometry which is nearest to our fractal Cantorian hyperbolic point-set geometry [40]. However our Cantor sets are both open and closed, i.e. clopen [44-46]. Noting what we said at the beginning, namely that real spacetime is more of a multifractal average than isotropic space, we are led via fractal and ultimate L logic of H. Wooden [39] to naively but correctly take the average of all the three cases. Thus our Cantorian K is effectively

This means our real Cantorian spacetime is clopen and pseudo flat which comes much nearer to the cosmic observation and measurement. Recalling now that we can also define a dimensionless density parameter

and therefore the matter distribution determines space geometry leading to [4]
1)  i.e.
i.e. 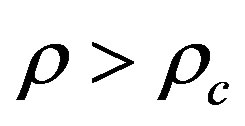 that means
that means 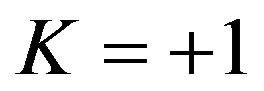
2)  i.e.
i.e. 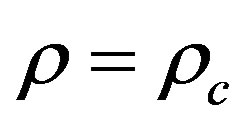 that means
that means 
3)  i.e.
i.e. 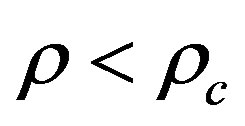 that means
that means 
where 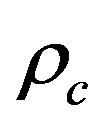 is the critical density. Consequently our model predicts via the same ultimate L logic [39] and provided that
is the critical density. Consequently our model predicts via the same ultimate L logic [39] and provided that  is larger than unity for
is larger than unity for 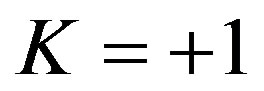 by almost the same amount it is smaller than unit for
by almost the same amount it is smaller than unit for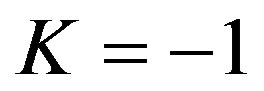 , we find that
, we find that
 .
.
Again this is in agreement with our mathematical model and current cosmic observation [1,2,44-46]. Taking the fact that our universe is clopen, pseudo flat and obeys Witten’s T-duality and generalized mirror symmetry where the 2-Adic norm of  is equal to that of quantum gravity
is equal to that of quantum gravity 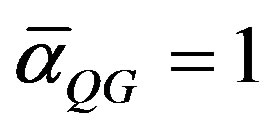 it can be shown that the topological speed of light is
it can be shown that the topological speed of light is  and that the topological Planck energy is
and that the topological Planck energy is . Using these values our present result follows directly with m = 5 from Magueijo-Smolin’s modified Einstein formula
. Using these values our present result follows directly with m = 5 from Magueijo-Smolin’s modified Einstein formula 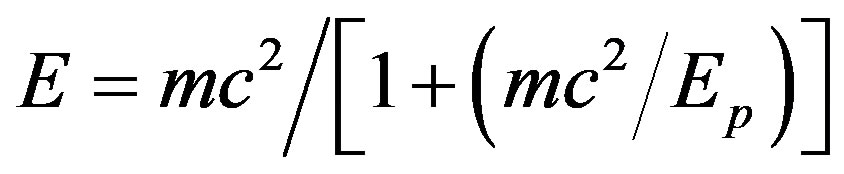 where Ep is the topological Planck energy as shown in [39,46].
where Ep is the topological Planck energy as shown in [39,46].
10. Dark Energy from Einstein’s Strength Criteria of the System of Equations
Einstein’s criteria of the strength of a system of equations in connection with general relativity is fairly well known [49]. It was also used on previous occasions for questions related to the unification of all fundamental forces and quantum gravity [4,25]. In this short section we outline a set of similar ideas to arrive from the classical 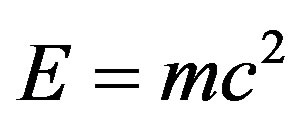 to the modified quantum relativity formula
to the modified quantum relativity formula . Our point of departure is related to Euclidean embedding however not the global Nash embedding used in earlier analysis but rather the local one attributed to Campbell [43]. Loosely speaking the theorem asserts that any reasonable Riemannian manifold can be locally embedded in a Ricci flat space with one more dimension. Taking advantage of Einstein’s general relativity and combining it with this theorem we are led naturally to a Nordstrom type of Kaluza-Klein theory [50] so that we will concentrate our attention on the strength of the system of equations related only to a higher dimensional Ricci tensor.
. Our point of departure is related to Euclidean embedding however not the global Nash embedding used in earlier analysis but rather the local one attributed to Campbell [43]. Loosely speaking the theorem asserts that any reasonable Riemannian manifold can be locally embedded in a Ricci flat space with one more dimension. Taking advantage of Einstein’s general relativity and combining it with this theorem we are led naturally to a Nordstrom type of Kaluza-Klein theory [50] so that we will concentrate our attention on the strength of the system of equations related only to a higher dimensional Ricci tensor.
As outlined in the superb book of Wesson [43] we also start from the Codazzi-Gauss equation and relate them to the said Ricci tensor which has  independent components. The components of this tensor must satisfy a system of three categories of Codazzi-Gauss equations obtained by contractions. The first set leads to as many equations as there are independent components, namely [4]
independent components. The components of this tensor must satisfy a system of three categories of Codazzi-Gauss equations obtained by contractions. The first set leads to as many equations as there are independent components, namely [4]
 .
.
The second set is simply n equations and the third is one scaler [4,43]. The total number of equations is thus [4,43]

Now we regard n as being not only the number of equations but also as a measure for the dimensionality of the geometrical objects constituting the space geometry which the Ricci tensor is describing. Thus for Einstein geometry we have a classical point with n = 0 and this leads not surprisingly to N(total) = 1. This is obviously the smallest number of equations possible and corresponds to maximally strong theory where E = mc2 is divided by unity giving us E(max) = mc2
as is well known. For the five dimensional Kaluza-Klein space we have a radically different Kaluza-Klein particle and thus Kaluza-Klein ‘geometrical’ points which are not zero points n = 0 but five dimensional points n = 5 [43,46]. In this case we find the number of equations goes up from 1 to 22:
N(total) = 22.
This is a much weaker theory and the corresponding Einstein energy density drops accordingly to

This is identical to the ordinary energy density of the quantum particle as shown previously using various other theories and methods [44-46].
It is interesting to see that five dimensions are indeed an optimal dimensionality to lead to unification of all fundamental interactions and that it is intimately connected to Witten’s D = 11 M-theory as well as D = 10 superstring theory all a part of E-infinity unit interval physics with the topological quantities  and
and  where
where , m is the topological 5D mass,
, m is the topological 5D mass,  is the topological speed of light and
is the topological speed of light and 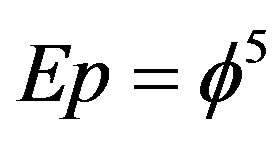 is the topological Planck energy or alternatively Hardy’s probability of quantum entanglement P(Hardy) =
is the topological Planck energy or alternatively Hardy’s probability of quantum entanglement P(Hardy) =  [43,46].
[43,46].
11. The Experimental Situation of E = mc2 and Its Revision to E = mc2/22
Having made substantial modification to E = mc2 a few words on the experimental situation are definitely in order at this point. There is a widespread misconception that E = mc2 (where E is the maximal energy, m is the rest mass and c is the speed of light) was tested to a very high degree of accuracy and is thus beyond revision. This is far from being an accurate description of the state of affairs regarding this arguably most famous of all equations [4]. In fact the opposite is true and with the benefit of hindsight we can say that it should have been clear from the beginning that most of the experiments conducted purporting to prove that E = mc2 are quantum experiments performed under classical and semi-classical assumptions as well as interpretations. A correct interpretation of classical experiments related to the validity of the correspondence principle would long ago have revealed that E = mc2 is not the complete story and would have prepared us for the relatively recent results of the COBE, MAP and supernova measurements and analysis and the ensuing introduction of the new concept of dark energy which took all of us with a huge surprise [1, 46,52]. In what follows we list the most obvious experiments which strongly hint at the afore mentioned misconception:
1) The correct interpretation of the famous COW experiment [55] as well as several refined versions of it all indicate a violation of the correspondence principle. Consequently there is no energy formula which can be exact and accurate without involving quantum theory, i.e. without quantum gravity or an effective quantum gravity theory [22,56].
2) Gravitational quanta were experimentally found, probably for the first time, by a Russian group led by V. V. Nesrizhevsky [57]. This is totally incompatible with a smooth continuous spacetime such as that of relativity and particularly E = mc2.
3) Quantum particles have no path. By contrast all experiments used in verifying E = mc2 discuss the set up and result in terms of a particle with a path which is a contradiction for an experiment which is aimed at solving a contradiction [7,9].
4) The cosmological measurements which led to the 2011 Nobel Prize in Physics all indicated that at a minimum something is amiss in standard relativity when probing extreme situations such as distances in the order of the Hubble radius [1,2,52].
5) The work of F. Zwiky as well as that of Magueijo, Moffat [53], Milgrom and Beckenstein apart of the flight of the Galileo probe as well as pioneer 10 and pioneer 11 [1,52] all show that something is not entirely right in the state of Denmark and as Shakespeare advises us in Hamlet: “There are more things in heaven and sky”. These things we hope we showed to be basically quantum spacetime itself or said a little more conservatively, it is the dark energy of a quantum wave which is devoid not only of matter and momentum but also of ordinary energy which is the privilege of the quantum particle only [45-47].
12. Conclusions
Whether we use E8E8 string theory, the holographic principle, the fractal M-theory or as done here, cosmic crystallography, the reduction in the energy predicted by Einstein is the same, namely a factor of 1/(22 + k) = 0.04508497187, i.e. a missing amount of dark energy equal to [1-3]
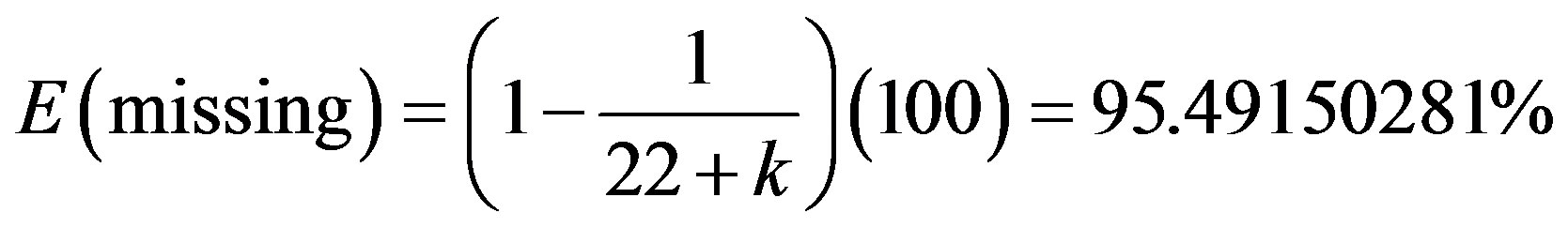 .
.
The simplest explanation of them all is that Einstein’s universe is superficially a smooth 4D space. On the other hand the real large scale structure of the real universe which respects its own fine structure (fractal-Cantorian) details is a self similar 11 dimensional space with the remarkable dimension (see Figures 3 and 4) [23,24]
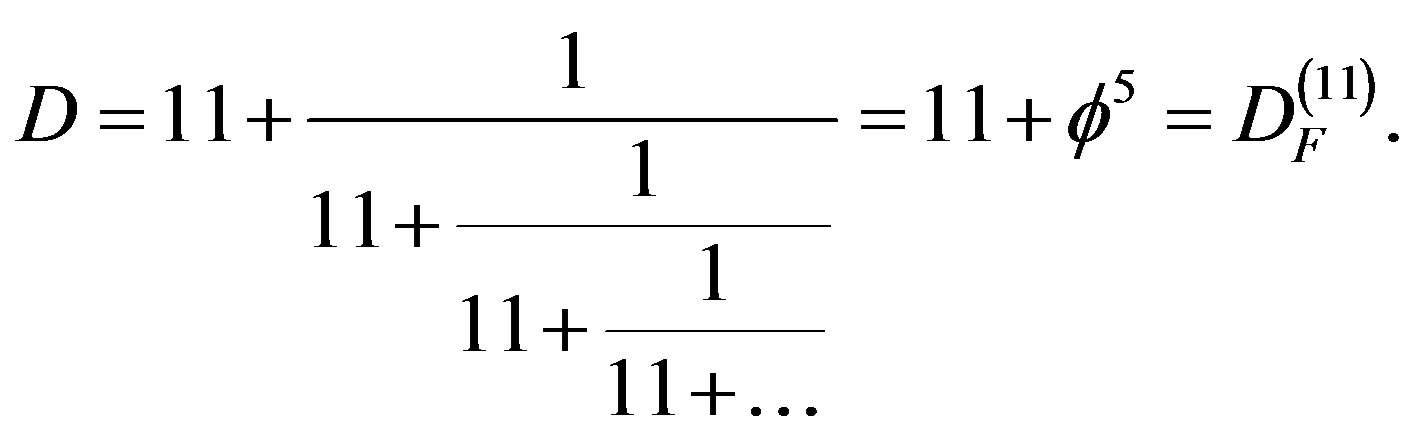
The kinetic energy equation
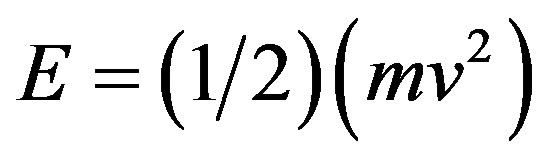
must therefore be rescaled down in accordance with the principle of scale relativity or the universal Weyl gauge theory [9,22,25] as follows
 .
.
Nottale’s scale relativity [3] gave an ingenious solution to this point long ago (see Figure 8) albeit approximately using logarithmic scale relativity rather than our present Cantorian golden mean based universal Weyl scaling [22,25]. Following the same strategy using the Poincaré dodecahedron would lead to equally satisfactory resolution of the issue of dark energy [1-4]. It is clear that fuzzy Hardy’s generic quantum entanglement in the form of fine structure added to Witten’s 11 dimensions of his M-theory produced a very powerful mathematical model, namely  dimensional spacetime theory capable of dealing with and correcting Einstein’s energy mass equation. Similar comments must be said about combining quantum Yang-Mills Theory with general relativity as explained in Figure 10. Finally in Figure 11, we summarized the methods of fractal logic as applied in deriving E of quantum relativity [41]. Some readers who are experimentally inclined may find the toy model for antigravity of Figure 14 quite amazing if not enlightening. In short we could say that the reason for the increased rate of cosmic expansion is in geometrical terms the anti-curvature of the compactified space dimensions while in physical terms it is the negative pressure of the dark energy of the quantum wave.
dimensional spacetime theory capable of dealing with and correcting Einstein’s energy mass equation. Similar comments must be said about combining quantum Yang-Mills Theory with general relativity as explained in Figure 10. Finally in Figure 11, we summarized the methods of fractal logic as applied in deriving E of quantum relativity [41]. Some readers who are experimentally inclined may find the toy model for antigravity of Figure 14 quite amazing if not enlightening. In short we could say that the reason for the increased rate of cosmic expansion is in geometrical terms the anti-curvature of the compactified space dimensions while in physical terms it is the negative pressure of the dark energy of the quantum wave.
It is important to draw attention to the validation of our main result, namely
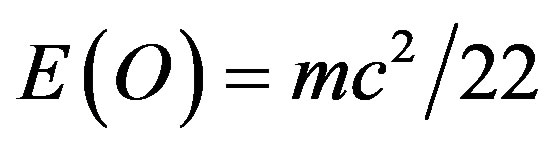 and
and 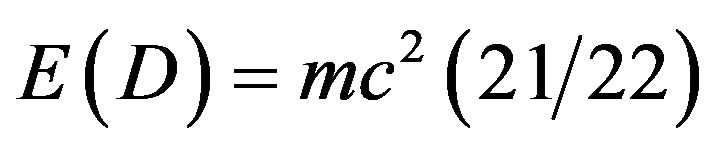
obtained by scaling the Planck scale following D. Gross idea [58] and using advanced transfinite set theory, and using a relatively mundane conventional method, namely varying the fine structure constant and replacing  by
by 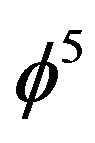 as explained in Figure 13 [51].
as explained in Figure 13 [51].
Nonetheless all of the above does not give still a quantum explanation of why we cannot measure dark energy directly. The complete answer to this question is the quantum particle wave duality [36]. Dark energy is the energy of the wave modeled by the empty set in five dimensional Kaluza-Klein spacetime [38,39,43]. Since measurement changes an empty set to zero set the wave change in to a particle. This is thus the collapse of the Hawking-Hartle wave function of the universe [34,36] which reduces energy to 4.5% and prevents the detection of the 95.5% propagation quantum kinetic energy [35], i.e. the dark energy. It is interesting to see how the energy formula for real energy is a straight forward application of the mathematical theory of intersection as shown in Figure 5. In addition and as presented in the chart of Figure 6, the relation between the zero set energy of the particle and the empty set energy of the wave is clearly a consequence of the particle wave duality of quantum mechanics and the topological fact that the wave is the cobordism of the particle. Finally one frequently overlooks the theoretical and experimental fact that quantum entanglement is nonlocal and separation in space has no meaning in that context. Therefore quantum entanglement has the same effect even on fantastically large length scales as explained in Figure 9. A short overview of the main conclusions and results of present work is given in Figure 12. Needless to say that in the present work we do addresses the issue of dark matter which is included in E = mc2 as the dark energy of the quantum wave. Nevertheless the vital question still leaves concerning whether the quantum wave and quantum spacetime are basically identical concepts or not in view of KAM theorem. That means harnessing the energy of the quantum wave could in fact be harnessed the energy of spacetime itself which is quite an old ideal situation between science fiction and science fact. Last but not least we state without explicit derivation which we reserves for future publication that our theory is implicitly a varying speed of light theory like that of Moffat and Magueijo’s explicit varying speed of light theory [53,54]. It may also be considered a doubly special relativity theory [54].
REFERENCES
- L. Amendola and S. Tsujikawa, “Dark Energy: Theory and Observations,” Cambridge University Press, Cambridge, 2010. doi:10.1017/CBO9780511750823
- Y. Baryshev and P. Teerikorpi, “Discovery of Cosmic Fractals,” World Scientific, Singapore, 2002.
- L. Nottale, “Scale Relativity,” Imperial College Press, London, 2011.
- R. Penrose, “The Road to Reality,” Jonathan Cape, London, 2004.
- J. Mageuijo and L. Smolin, “Lorentz Invariance with an Invariant Energy Scale,” Physical Review Letters, Vol. 88, No. 19, 2002, Article ID: 190403.
- J.-P. Luminet, “The Wraparound Universe,” A.K. Peters Ltd., Wellesley, 2008.
- M. S. El Naschie, “The Crystallographic Space Groups and Heterotic String Theory,” Chaos, Solitons & Fractals, Vol. 41, No. 5, 2009, pp. 2282-2284. doi:10.1016/j.chaos.2008.09.001
- J. R. Weeks, “The Shape of Space,” Marcel Dekker, New York, 2002.
- L. Marek-Crnjac, “The Hausdorff Dimension of the Penrose Universe,” Physics Research International, Vol. 2011, 2011, Article ID: 874302.
- I. Aitchison, “Super Symmetry in Particle Physics,” Cambridge University Press, Cambridge, 2007.
- A. Elokaby, “The Deep Connection between Instantons and String States Encoded in Klein’s Modular Space,” Chaos, Solitons & Fractals, Vol. 42, No. 1, 2009, pp. 303-305. doi:10.1016/j.chaos.2008.12.001
- M. S. El Naschie, “Anomalies Free E-Infinity from von Neumann’s Continuous Geometry,” Chaos, Solitons & Fractals, Vol. 38, No. 5, 2008, pp. 1318-1322. doi:10.1016/j.chaos.2008.06.025
- M. S. El Naschie, “Quasi Exceptional E12 Lie Symmetry Group with 685 Dimensions, KAC-Moody Algebra and E-Infinity Cantorian Spacetime,” Chaos, Solitons & Fractals, Vol. 38, No. 4, 2008, pp. 990-992. doi:10.1016/j.chaos.2008.06.015
- M. S. El Naschie, “Average Exceptional Lie and Coxeter Group Hierarchies with Special Reference to the Standard Model of High Energy Particle Physics,” Chaos, Solitons & Fractals, Vol. 37, No. 3, 2008, pp. 662-668. doi:10.1016/j.chaos.2008.01.018
- M. S. El Naschie, “KAC-Moody Exceptional E12 from Simplictic Tiling,” Chaos, Solitons & Fractals, Vol. 41, No. 4, 2009, pp. 1569-1571. doi:10.1016/j.chaos.2008.06.020
- M. S. El Naschie, “The Internal Dynamics of the Exceptional Lie Symmetry Groups Hierarchy and the Coupling Content of Unification,” Chaos, Solitons & Fractals, Vol. 38, No. 4, 2008, pp. 1031-1038.
- M. S. El Naschie, “High Energy Physics and the Standard Model from the Exceptional Lie Groups,” Chaos, Solitons & Fractals, Vol. 36, No. 1, 2008, pp. 1-17. doi:10.1016/j.chaos.2007.08.058
- M. S. El Naschie, “Symmetry Group Prerequisites for E-Infinity in High Energy Physics,” Chaos, Solitons & Fractals, Vol. 35, No. 1, 2008, pp. 202-211. doi:10.1016/j.chaos.2007.05.006
- M. S. El Naschie, “Fuzzy Knot Theory Interpretation of Yang-Mills Instantons and Witten’s 5-Brane Model,” Chaos, Solitons & Fractals, Vol. 38, No. 5, 2008, pp. 1349-1354. doi:10.1016/j.chaos.2008.07.002
- J.-H. He, “Hilbert Cube Model for Fractal Spacetime,” Chaos, Solitons & Fractals, Vol. 42, No. 5, 2009, pp. 2754-2759. doi:10.1016/j.chaos.2009.03.182
- M. S. El Naschie, “An Irreducibly Simple Derivation of the Hausdorff Dimension of Spacetime,” Chaos, Solitons & Fractals, Vol. 41, No. 5, 2009, pp. 1902-1904. doi:10.1016/j.chaos.2008.07.043
- M. S. El Naschie, “A Review of E-Infinity and the Mass Spectrum of High Energy Particle Physics,” Chaos, Solitons & Fractals, Vol. 19, No. 1, 2004, pp. 209-236. doi:10.1016/S0960-0779(03)00278-9
- M. S. El Naschie, “On an Eleven Dimensional E-Infinity Fractal Spacetime Theory,” International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 7, No. 4, 2006, pp. 407-409.
- M. S. El Naschie, “The Discrete Charm of Certain Eleven Dimensional Spacetime Theory,” International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 7, No. 4, 2006, pp. 477-481.
- M. S. El Naschie, “The Theory of Cantorian Spacetime and High Energy Particle Physics (An Informal Review),” Chaos, Solitons & Fractals, Vol. 41, No. 5, 2009, pp. 2635-2646. doi:10.1016/j.chaos.2008.09.059
- J.-H. He, et al., “Quantum Golden Mean Entanglement Test as the Signature of the Fractality of Micro Spacetime,” Nonlinear Science Letters B, Vol. 1, No. 2, 2011, pp. 45-50.
- M. S. El Naschie, “Quantum Entanglement as a Consequence of a Cantorian Micro Spacetime Geometry,” Journal of Quantum Information Science, Vol. 1, No. 2, 2011, pp. 50-53. doi:10.4236/jqis.2011.12007
- M. S. El Naschie, “Derivation of the Euler Characteristic and Curvature of Cantorian Fractal Spacetime Using Nash Euclidean Embedding and the Universal Menger Sponge,” Chaos, Solitons & Fractals, Vol. 41, No. 5, 2009, pp. 2394-2398. doi:10.1016/j.chaos.2008.09.021
- M. S. El Naschie, “Arguments for Compactness and Multiple Connectivity of Our Cosmic Spacetime,” Chaos, Solitons & Fractals, Vol. 41, No. 5, 2009, pp. 2787-2789. doi:10.1016/j.chaos.2008.10.011
- M. S. El Naschie, “Light Cone Quantization, Heterotic Strings and E-Infinity Derivation of the Number of Higgs Bosons,” Chaos, Solitons & Fractals, Vol. 23, No. 5, 2005, pp. 1931-1933. doi:10.1016/j.chaos.2004.08.004
- M. S. El Naschie, “Fuzzy Platonic Spaces as a Model for Quantum Physics,” Mathematical Models, Physical Methods and Simulation in Science & Technology, Vol. 1, No. 1, 2008, pp. 69-90.
- M. S. El Naschie, “Hilbert Space, Poincaré Dodecahedron and Golden Mean Transfiniteness,” Chaos, Solitons & Fractals, Vol. 31, No. 4, 2007, pp. 787-793. doi:10.1016/j.chaos.2006.06.003
- M. S. El Naschie, “Transfinite Harmonization by Taking the Dissonance Out of the Quantum Field Symphony,” Chaos, Solitons & Fractals, Vol. 36, No. 4, 2008, pp. 781-786. doi:10.1016/j.chaos.2007.09.018
- S. Nakajima, et al., “Foundations of Quantum Mechanics in the Light of New Technologies,” World Scientific, Singapore, 1996.
- W. Rindler, “Relativity (Special, General and Cosmological),” Oxford University Press, Oxford, 2004.
- G. W. Gibbons, et al., “The Future of Theoretical Physics and Cosmology,” Cambridge University Press, Cambridge, 2003.
- S. Hawking, et al., “Brane New World,” Physical Review D, Vol. 62, No. 4, 2000, Article ID: 043501. doi:10.1103/PhysRevD.62.043501
- M. S. El Naschie, “A Unified Newtonian-Relativistic Quantum Resolution of the Supposedly Missing Dark Energy of the Cosmos and the Constancy of the Speed of Light,” International Journal of Modern Nonlinear Theory and Application, Vol. 2, No. 1, 2013, pp. 43-54. doi:10.4236/ijmnta.2013.21005
- L. Marek-Crnjac, et al., “Chaotic Fractals at the Root of Relativistic Quantum Physics and Cosmology,” International Journal of Modern Nonlinear Theory and Application, Vol. 2, No. 1A, 2013, pp. 78-88.
- M. S. El Naschie, “The Hyperbolic Extension of Sigalotti-Hendi-Sharifzadeh’s Golden Triangle of Special Theory of Relativity and the Nature of Dark Energy,” Journal of Modern Physics, Vol. 4, No. 3, 2013, pp. 354- 356. doi:10.4236/jmp.2013.43049
- M. S. El Naschie, S. Olsen, J. H. He, S. Nada, L. Marek-Crnjac, A. Helal, et al., “On the Need for Fractal Logic in High Energy Quantum Physics,” International Journal of Modern Nonlinear Theory and Application, Vol. 1, No. 3, 2012, pp. 84-92. doi:10.4236/ijmnta.2012.13012
- J. Guckenheimer and P. Holmes, “Nonlinear Dynamical Systems and Bifurcation of Vector Fields,” Springer Verlag, New York, 1994.
- P. S. Wesson, “Five-Dimensional Physics,” World Scientific, Singapore, 2006.
- F. Morgan, “Geometric Measure Theory,” Academic Press, Amsterdam, 2009.
- M. S. El Nasche, “A Fractal Menger Sponge Spacetime Proposal to Reconcile Measurements and Theoretical Predictions of Cosmic Dark Energy,” International Journal of Modern Nonlinear Theory and Application, Vol. 2, No. 2, 2013, pp. 107-121.
- M. S. El Naschie, “Quantum Entanglement: Where Dark Energy and Negative Gravity plus Accelerated Expansion of the Universe Comes from,” Journal of Quantum Information Science, Vol. 3, No. 2, 2013, pp. 57-77. doi:10.4236/jqis.2013.32011
- M. S. El Naschie, “Dark Energy from Kaluza-Klein Spacetime and Noether’s Theorem via Lagrangian Multiplier Method,” Journal of Modern Physics, Vol. 4, No. 6, 2013, pp. 757-760. doi:10.4236/jmp.2013.46103
- M. S. El Naschie, “Elementary Prerequisites for E-Infinity,” Chaos, Solitons & Fractals, Vol. 30, No. 3, 2006, pp. 579-605. doi:10.1016/j.chaos.2006.03.030
- B. Kosko, “Fuzzy Thinking,” Flamingo-Harper Collins Publishers, London, 1993.
- M. S. El Naschie, “Is Einstein’s General Field Equation More Fundamental than Quantum Mechanics and Particle Physics,” Chaos, Solitons & Fractals, Vol. 30, No. 3, 2006, pp. 525-531. doi:10.1016/j.chaos.2005.04.123
- P. Halpern, “The Great Beyond,” John Wiley & Sons, New York, 2004.
- E. J. Copeland, M. Sami and S. Tsujikawa, “Dynamics of Dark Energy,” International Journal of Modern Physics D, Vol. 15, No. 11, 2006, pp. 1753-1936.
- J. Magueijo and J. W. Moffat, “Comments on ‘Note on Varying Speed of Light Theories’,” General Relativity and Gravitation, Vol. 40, 2007, pp. 1797-1803.
- J. Magueijo and L. Smolin, “Gravity’s Rainbow,” Classical and Quantum Gravity, Vol. 21, No. 7, 2004, p. 1725.
- R. Calella, A. Woverhauser and S. A. Werner, “Observation of Gravitationally Induced Quantum Interference,” Physical Review Letters, Vol. 34, No. 23, 1975, pp. 1472-1474. doi:10.1103/PhysRevLett.34.1472
- M. S. El Naschie, “A Resolution of the Cosmic Dark Energy via Quantum Entanglement Relativity Theory,” Journal of Quantum Information Science, Vol. 3, No. 1, 2013, pp. 23-26. doi:10.4236/jqis.2013.31006
- V. V. Nesvizhevky and A. K. Petukhov, “Study of Neutron Quantum States in the Gravity Field,” European Physical Journal C, Vol. 40, No. 4, 2005, p. 479. doi:10.1140/epjc/s2005-02135-y
- D. Gross, “Can We Scale the Planck Scale?” Physics Today, Vol. 42, No. 6, 1989, p. 9.

