International Journal of Astronomy and Astrophysics
Vol. 3 No. 2 (2013) , Article ID: 33238 , 6 pages DOI:10.4236/ijaa.2013.32021
Cosmological Distances in Five General Cosmic Models
Department of Astronomy, Faculty of Science, King Abdulaziz University, Jeddah, Saudi Arabia
Email: flbukhari@hotmail.com
Copyright © 2013 Fadel A. Bukhari. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 3, 2013; revised February 4, 2013; accepted February 12, 2013
Keywords: Extragalactic Distances; Cosmology; Cosmic Dynamics
ABSTRACT
Four cosmological distances were investigated in the light of the five general cosmic models which were developed in a previous study. These are the proper distance, luminosity distance, angular diameter distance and distance modulus. Each of these distances was studied in terms of the redshift of the extragalactic objects. Estimations of the horizon distance of the universe, the total mass and the mass of matter within the horizon distance, the equivalent numbers of the Milky Way-like galaxies and the Coma-like clusters of galaxies to the mass of matter were determined in the general models at the present time.
1. Introduction
One of the most interesting aspects of investigating cosmic models is determination of cosmological distances of the extragalactic objects in these models such as the proper distance, luminosity distance, angular diameter distance (the proper distance of the object when its light was emitted) and distance modulus.
In a previous study five general cosmic models were developed using comprehensive selection ratios of the universe components which are luminous matter, dark matter, photons, neutrinos, and dark energy [1]. Although some physical properties of the universe were discussed in these models, we concentrate in this article on precise determination of cosmic distances of the extragalactic objects in terms of their redshifts.
The importance of this study comes from the fact that the cosmic distances mentioned above are most commonly used in many cosmological researches. As a consequence of specifying cosmic distances, interesting estimations were computed in the general models at the present time. These estimations are horizon distance, total mass within the horizon distance, mass of matter (luminous and dark matter) within the horizon distance, and its equivalent numbers of both the Milky Way-like galaxies and the Coma-like clusters.
Description of methodology is given in Section 2, while results are presented in Section 3, accuracy and errors are illustrated in Section 4, and discussion and conclusion are shown in Section 5.
2. Methodology
The proper distance of an extragalactic object at present time  is given by
is given by
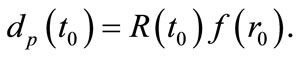 (1)
(1)
where 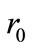 is the radial comoving coordinate of the object now, and
is the radial comoving coordinate of the object now, and  is expressed as
is expressed as
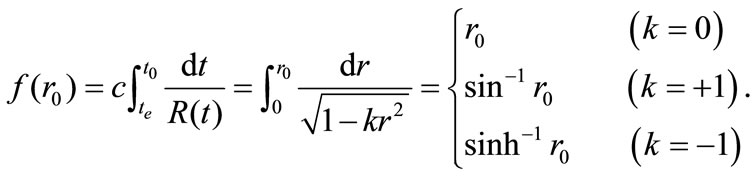 (2)
(2)
where  is the scale factor of the universe expansion,
is the scale factor of the universe expansion, 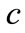 the speed of light,
the speed of light, 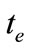 the emission time of the object photon and
the emission time of the object photon and 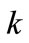 the curvature of space in the universe. Let
the curvature of space in the universe. Let  then Equation (2) becomes
then Equation (2) becomes
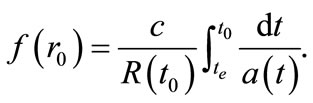 (3)
(3)
Substituting by Equation (3) in Equation (1) we get
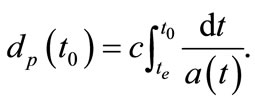 (4)
(4)
From [1] we have seen that the expansion speed of the universe is
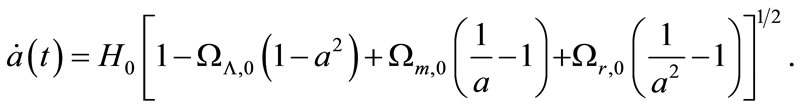 (5)
(5)
where  and
and  are the density parameters of the dark energy, matter and radiation at the present time respectively.
are the density parameters of the dark energy, matter and radiation at the present time respectively. 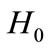 is the Hubble parameter at the present time. Equation (5) can be written as
is the Hubble parameter at the present time. Equation (5) can be written as
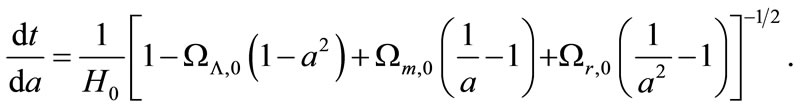 (6)
(6)
Substituting by Equation (6) in Equation (4) we find
 (7)
(7)
where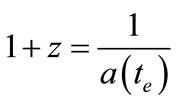 ,
, 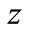 is the redshift of the object.
is the redshift of the object.
The luminosity distance 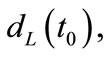 angular diameter distance
angular diameter distance  and distance modulus of the object at the present time are expressed respectively as
and distance modulus of the object at the present time are expressed respectively as
 (8)
(8)
 (9)
(9)
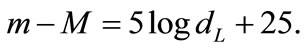 (10)
(10)
where 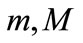 are the apparent and absolute magnitudes of the object. The distances
are the apparent and absolute magnitudes of the object. The distances 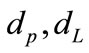 and
and 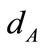 are measured in Mpc.
are measured in Mpc.
It is obvious from Equation (7) that the horizon distance of the universe at the present time is given by
 (11)
(11)
where 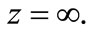 The Robertson-Walker metric of spacetime which describes the expansion or contraction of homogeneous and isotropic universe is given by
The Robertson-Walker metric of spacetime which describes the expansion or contraction of homogeneous and isotropic universe is given by
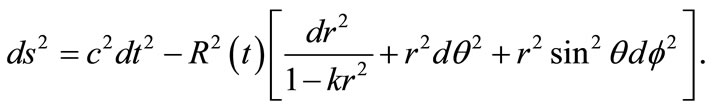 (12)
(12)
where  are the comoving coordinates of a point in space. The volume of three dimensional sphere can be written as
are the comoving coordinates of a point in space. The volume of three dimensional sphere can be written as
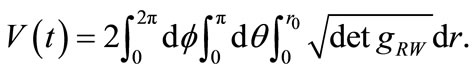 (13)
(13)
where 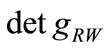 is the determinant of the spatial part of the Robertson-Walker metric matrix and given by
is the determinant of the spatial part of the Robertson-Walker metric matrix and given by
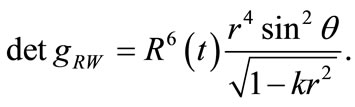 (14)
(14)
Since the space of the universe is flat at the present time, hence 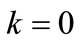 and
and
 (15)
(15)
Substituting by (15) in (13) we have

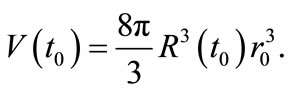 (16)
(16)
For flat space (1) and (2) give
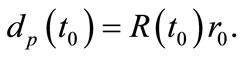 (17)
(17)
Substituting by (17) in (16) we get at the present time
 (18)
(18)
Similarly the volume of sphere of radius  is expressed as
is expressed as
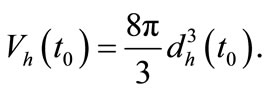 (19)
(19)
From the previous study [1] it is obvious that at any given cosmic time the total density of the universe is given by



or
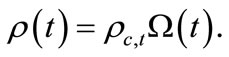 (20)
(20)
where the parameters 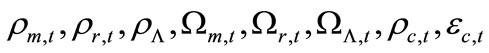 and
and  are all defined exactly as in the previous study. At the present time Equation (20) gives
are all defined exactly as in the previous study. At the present time Equation (20) gives
 (21)
(21)
The total mass within  is given by Equations (19), (21) as
is given by Equations (19), (21) as
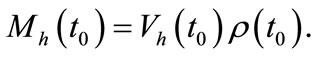 (22)
(22)
The mass of matter within 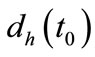 is
is

or
 (23)
(23)
Since the masses of the Milky Way galaxy 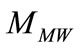 and the Coma cluster
and the Coma cluster  are
are  , [2], where
, [2], where 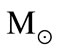 is the solar mass. Therefore the equivalent numbers of the Milky Way-like galaxies and the Coma-like clusters to
is the solar mass. Therefore the equivalent numbers of the Milky Way-like galaxies and the Coma-like clusters to 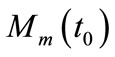 are respectively
are respectively
 (24)
(24)
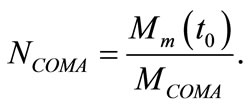 (25)
(25)
3. Results and Discussion
The proper distance-redshift relation (7) in the general models up to  is plotted in Figure 1, where the distributions increase with
is plotted in Figure 1, where the distributions increase with  and they coincide on each other for
and they coincide on each other for 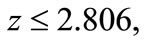 but they slightly diverge from each other afterwards such that the distributions of the general models
but they slightly diverge from each other afterwards such that the distributions of the general models  and
and  are at the top followed by those of the general models
are at the top followed by those of the general models 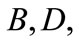 and
and  respectively.
respectively.
The distributions of the luminosity distance-redshift relation in the general models up to  are shown in Figures 2(a)-(e). In each figure the upper curve represents Equation (8) and the lower curve represents the relation
are shown in Figures 2(a)-(e). In each figure the upper curve represents Equation (8) and the lower curve represents the relation
 (26)
(26)
where  is the decelerating parameter of the universe at the present time [3,4]. It is noticeable that
is the decelerating parameter of the universe at the present time [3,4]. It is noticeable that 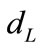 continuously raises with
continuously raises with 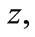 however, Equation (26) gives less estimation of
however, Equation (26) gives less estimation of 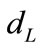 than that of Equation (8) for
than that of Equation (8) for
 and the difference between the two estimations increases also with
and the difference between the two estimations increases also with 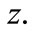 This is due to the repulsive effect of the dark energy. Initially, when the universe has small volume the effect of gravity is greater than the effect of dark energy, so the initial expansion rate of the universe is slow just as in Friedmaun models. However, there will come a point when the repulsive effect of the dark energy will equal and then exceeds the effect of gravity and the universe will expand in continuously increasing rate. In this case, distant galaxies will have greater distances from us than their distances in the case of the Friedmaun models [5].
This is due to the repulsive effect of the dark energy. Initially, when the universe has small volume the effect of gravity is greater than the effect of dark energy, so the initial expansion rate of the universe is slow just as in Friedmaun models. However, there will come a point when the repulsive effect of the dark energy will equal and then exceeds the effect of gravity and the universe will expand in continuously increasing rate. In this case, distant galaxies will have greater distances from us than their distances in the case of the Friedmaun models [5].
Figure 3 illustrates the distributions of the angular diameter distance—redshift relation (9) in the general models up to 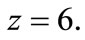 These distributions coincide on each other for
These distributions coincide on each other for  then they start diverging slightly from each other with the distributions of the general models
then they start diverging slightly from each other with the distributions of the general models 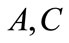 and
and 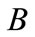 are at the top followed by those of the general models
are at the top followed by those of the general models 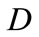 and
and  respectively. All distributions raise up appreciably fast until the value
respectively. All distributions raise up appreciably fast until the value  given in each general model in Table 1, then the distributions decrease gradually with increasing
given in each general model in Table 1, then the distributions decrease gradually with increasing 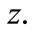
The distance modulus-redshift relation is determined using Equations (8) and (10) and represented by the
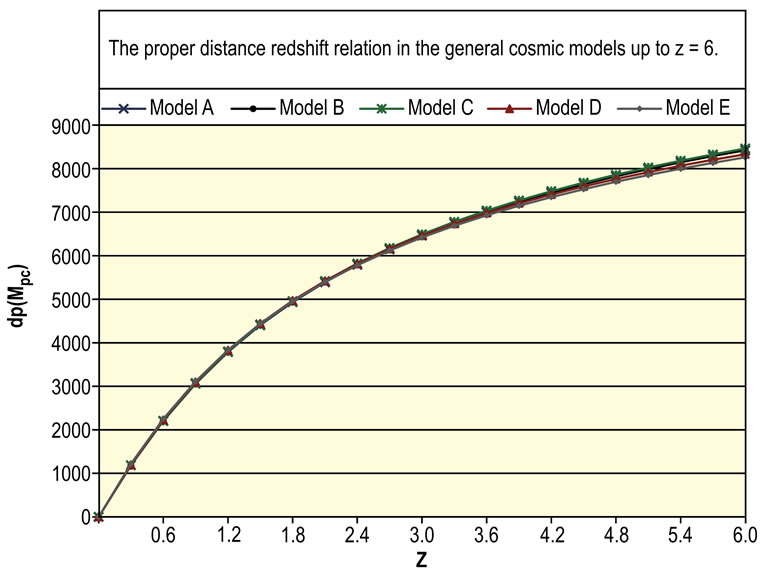
Figure 1. The proper distance redshift relation in the general cosmic models up to z = 6.
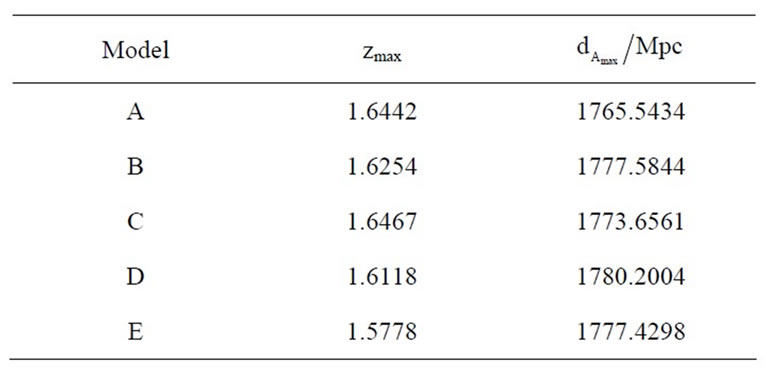
Table 1. Maximum values of the angular diameter distances in the general cosmic models.
 (a)
(a) (b)
(b)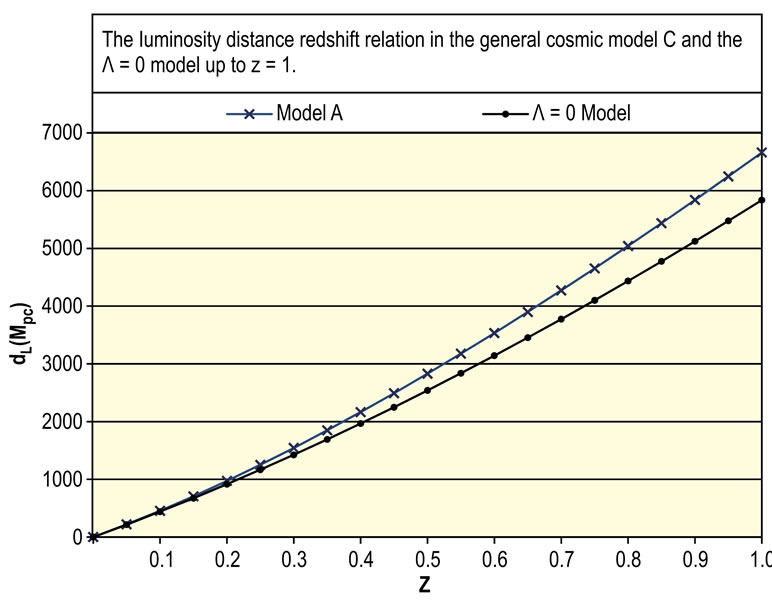 (c)
(c)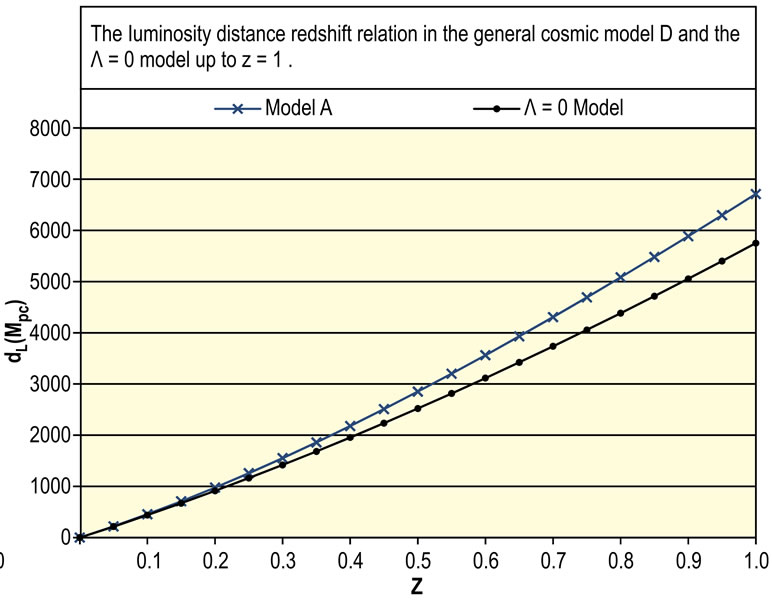 (d)
(d)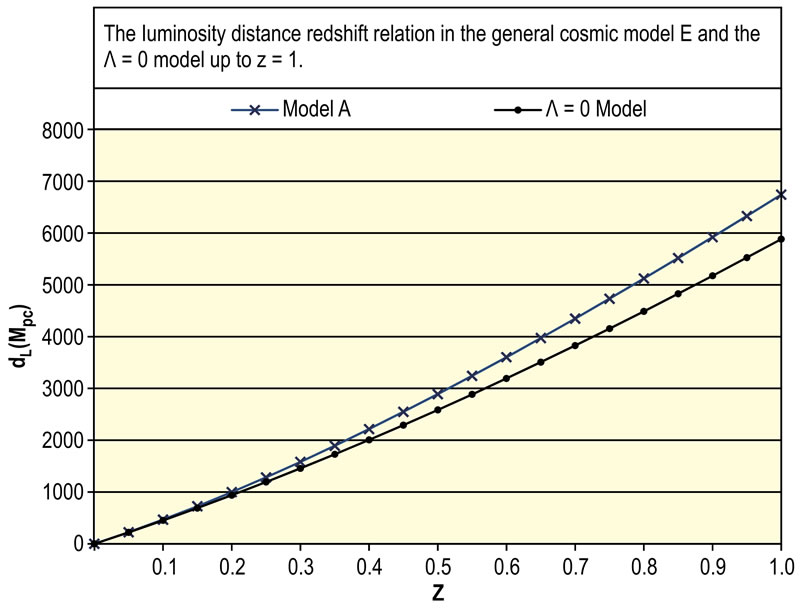 (e)
(e)
Figure 2. (a) The luminosity distance redshift relation in the general cosmic model A and Λ = 0 model up to z = 1; (b) The luminosity distance redshift relation in the general cosmic model B and Λ = 0 model up to z = 1; (c) The luminosity distance redshift relation in the general cosmic model C and Λ = 0 model up to z = 1; (d) The luminosity distance redshift relation in the general cosmic model D and Λ = 0 model up to z = 1; (e) The luminosity distance redshift relation in the general cosmic model E and Λ = 0 model up to z = 1.
distributions in the general models up to 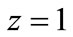 exhibited in Figure 4. It is prominent that
exhibited in Figure 4. It is prominent that 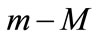 increases continuously with
increases continuously with 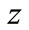 in all general models, and the distributions of these models coincide on each other.
in all general models, and the distributions of these models coincide on each other.
Values of 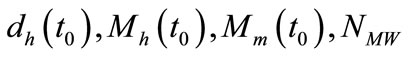 and
and 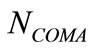 were computed in the general models at the present time using Equations (11) and (22)-(25) respectively. These values and their possible ranges are shown in Table 2. More details about calculations of these estimations are given in the next section.
were computed in the general models at the present time using Equations (11) and (22)-(25) respectively. These values and their possible ranges are shown in Table 2. More details about calculations of these estimations are given in the next section.
4. Accuracy and Errors
In computing the proper distance 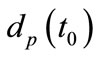 of an extragalactic object at the present time in terms of its redshift
of an extragalactic object at the present time in terms of its redshift  one can get an average value of
one can get an average value of 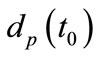 to good degree of accuracy by applying Equation (7), where the parameters
to good degree of accuracy by applying Equation (7), where the parameters 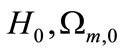 and
and 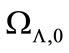 have their average values in the general model
have their average values in the general model 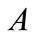 obtained from [1].
obtained from [1].
Nevertheless, more accurate value of  can be obtained by calculating
can be obtained by calculating  in all the possible observed 163 models of the case A [1]. Assume the average of these 163 values of
in all the possible observed 163 models of the case A [1]. Assume the average of these 163 values of  is
is 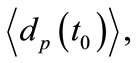 and the maximum and minimum values of
and the maximum and minimum values of 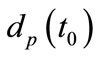 are
are
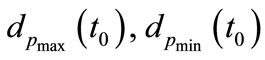 respectively. Let
respectively. Let 
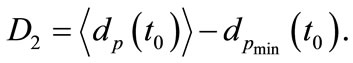 Then the accurate value of the proper distance of the extragalactic object is
Then the accurate value of the proper distance of the extragalactic object is
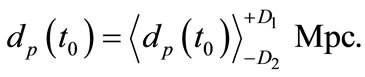 (27)
(27)
This procedure was used to determine the average estimations of the parameters  and
and 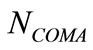 with their possible ranges in the general models as illustrated in Table 2.
with their possible ranges in the general models as illustrated in Table 2.
5. Conclusions
In this paper distributions of the proper distance, luminosity distance, angular diameter distance and distance modulus were investigated in terms of the redshift of an
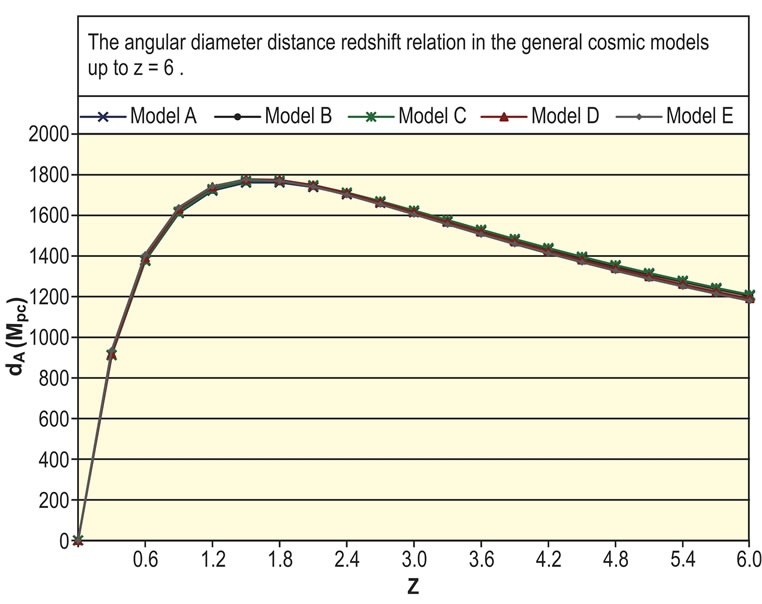
Figure 3. The angular diameter distance redshift relation in the general cosmic models up to z = 6.
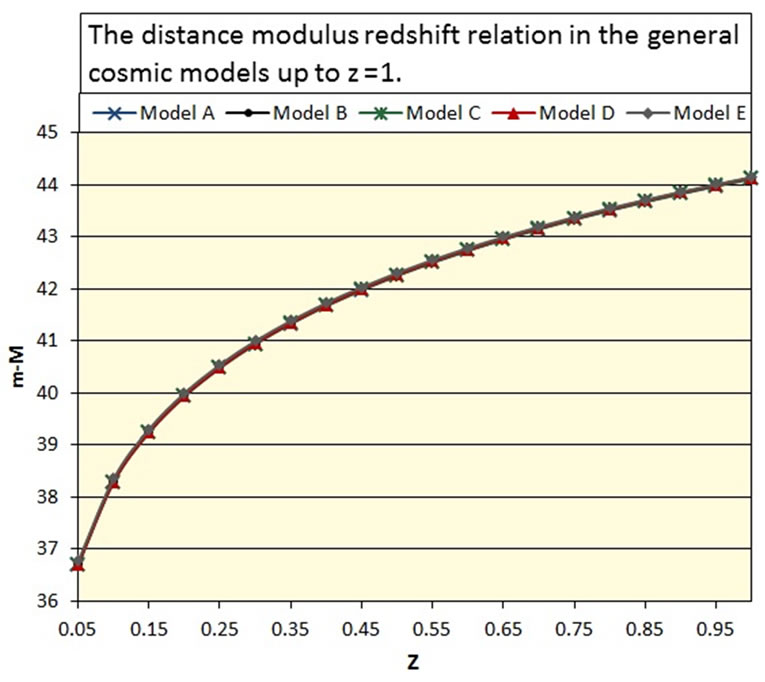
Figure 4. The distance modulus redshift relation in the general cosmic models up to z = 6.

Table 2. Estimation of the horizon distance , the total mass and the mass of matter within the horizon distance, the equivalent numbers of the Milky way-like galaxies and the Coma-like clusters to the mass of matter in the general cosmic models at the present time.
extragalactic object in the light of the five general cosmic models which were constructed in a previous paper. It is found that all of these cosmological distances increase continuously with redshift except the angular diameter distance which increases very rapidly with redshift to maximum value and then it decreases gradually with increasing 
Calculations of the horizon distance, the total mass and the mass of matter within the horizon distance, the equivalent numbers of the Milky Way-like galaxies and the Coma-like clusters of galaxies to the mass of matter were all obtained in the general cosmic models at the present time.
6. Acknowledgements
This paper was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah. The author, therefore, acknowledges with thanks DSR technical and financial support.
REFERENCES
- F. A. Bukhari, “Journal of King Abdulaziz University: Science,” 2013.
- B. Ryden, “Introduction to Cosmology,” Addison & Wesley, Boston, 2003.
- S. Weinberg, “Gravitation and Cosmology,” John Wiley & Sons, Ltd., Hoboken, 1972.
- J. N. Islam, “An Introduction to Mathematical Cosmology,” Cambridge University Press, Cambridge, 2002.
- I. Morison, “Introduction to Astronomy and Cosmology,” John Wiley & Sons, Ltd., Hoboken, 2008.

