Advances in Chemical Engineering and Science
Vol.04 No.04(2014), Article ID:50918,8 pages
10.4236/aces.2014.44055
Prediction of Kappa Number in Eucalyptus Kraft Pulp Continuous Digester Using the Box & Jenkins Methodology
Flávio M. Correia1*, José V. Hallak d’Angelo1, Roger J. Zemp1, Sueli A. Mingoti2
1Chemical Engineering Faculty, UNICAMP—University of Campinas, Campinas, Brazil
2Department of Statistic, UFMG—Federal University of Minas Gerais, Belo Horizonte, Brazil
Email: *flaviomcorreia@uol.com.br
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 August 2014; revised 16 September 2014; accepted 10 October 2014
ABSTRACT
The quality of the resulting pulping continuous digesters is monitored by measuring the Kappa number, which is a reference of residual lignin. The control of the kappa number is carried out mainly in the top of the digester, therefore it is important to get some indication of this analysis beforehand. In this context, the aim of this work was to obtain a prediction model of the kappa number in advance to the laboratory results. This paper proposes a new approach using the Box & Jenkins methodology to develop a dynamic model for predicting the kappa number from a Kamyr continuous digester from an eucalyptus Kraft pulp mill in Brazil. With a database of 1500 observations over a period of 30 days of operation, some ARMA models were studied, leading to the choice of ARMA (1, 2) as the best forecasting model. After fitting the model, we performed validation with a new set of data from 30 days of operation, achieving a model of 2.7% mean absolute percent error.
Keywords:
Continuous Digester, Kappa Number Prediction, Time Series, Box & Jenkins

1. Introduction
For the past years, the pulp mill engineers have faced the task of doing better with less. The process industries face considerable control challenges, especially in the consistent production, high quality, stable operation and more efficient use of raw materials and energy. Kraft pulping is a complex mix of nonlinear, multivariable and interactive chemical and physical processes. The pulp digester is one of the major unit operations in the pulp mill and its proper control is very important to the all pulp production steps. Kappa number, which is the main control variable, is sampled infrequently and usually long time delays associated with its measurements. Considering the long process time delays between many of the important variables affecting digester performance and kappa number, an inferential model for this important measure would be very useful. In continuous digester, the control of the kappa number is carried out mainly in the top of the equipment; therefore it is important to get some indication of the quality beforehand. The residence time from the top to the bottom of the digester (where kappa number is measured) is about 3 - 5 hours.
Forecasting plays a central role in the efficient operation of chemical reactors, as it provides valuable information on the expected future direction of various factors. Modeling and identification are important parts of a good control and fault diagnosis systems. In this work, inferential models for kappa number from a eucalyptus Kraft pulp Kamyr digester are developed using the method of time series of Box & Jenkins [1] .
2. Kraft Pulping
Among all the processes in the pulp industry, the delignification of woodchips plays the most vital role. The continuous pulp digester is the equipment designed to convert chips into a cellulose fiber pulp. Lignin serves to hold the cellulose fibers and other elements and binding them together into the anatomical structure of the wood. Lignin is a complex, three-dimensional polymer containing mostly phenyl propane units joined together by various ether and carbon-carbon linkages. Lignin is susceptible to degradation and dissolution by treatment with strong bases under elevated temperatures. Thus, lignin can be removed from the wood, leaving separated cellulose fibers in the form of a pulp. The main quality parameter for the pulp is the Kappa number, which is a reference for the amount of lignin in the wood. During Kraft pulping, it is necessary to remove as much lignin as possible with minimum loss or degradation of the carbohydrate groups. Aim of the Kraft pulping processes is to deliberate the lignin by dissolving or degradation [2] .
The pulping of the wood is accomplished by cooking them in a heated causticizing solution of NaOH and NA2S, known as white liquor. The digester is essentially a tubular reactor, where chips flow from the inlet at the top to the outlet at the bottom of the digester. The chip column is heated up by various circulation systems as it moves downwards. It consists of some zones where the flow of white liquor is either in co-current or in counter-current with respect to the chips flow, dependent on the functional zone. A schematic overview of the digester and its functional zones is given in Figure 1.
In case of single vessel, pre-steamed chips and white liquor are fed into the continuous digester. At the top of the digester, they are heated to reach the cooking temperature using direct steam. Temperatures in this zone are around 120˚C - 140˚C, and pressure around 8 - 9 kg/cm2. In the impregnation zone chips are brought into contact with a co-current flow of white liquor, starting the diffusion into the woodchips porous and the delignification reaction slowly begins. In order to reach the required reaction temperatures, in the various zones part of the white liquor flow is drawn off the digester. The white liquor is supplied through a system of concentric pipes. After being heated in external heat exchangers, the white liquor flow is fed back into the heating zone for gradually heating the white liquor to the desired reaction temperatures (150˚C - 160˚C). The majority of the delignification takes place in this section where the pulp Kappa number is drastically reduced.
A concentric pipe ending above the end of the cooking zone injects a relatively cold, washing liquor flow. The temperature of the chips is reduced and the delignification reactions are quenched. The quench liquor is a process flow coming from the digester, referred to as black liquor. In the washing zone, a counter current flow washes the degradation products from the pulp. In the counter current region a large average driving force is maintained between the chips and the washing liquor. A process flow referred to as dilution liquor is used as washing liquor. In an actual digester, a part of the wash liquor is fed into the digester through the cold blow line, which prevents caking of the pulp in the bottom of the digester. The temperature of the wash liquor has a large influence on the pulp quality. As diffusion is favored by high temperatures, more degradation products are washed from the pulp at higher temperatures. However, too high temperatures cause continuation of the delignification process, damaging the cellulose fibers structure producing a lower pulp viscosity. In the cooling zone, part of the injected filtrate flow goes down and thus travels co-current with respect to the chips. At the bottom of this zone, the outlet device is located.
The final cooking result (kappa number) is achieved from the digester blow line by using laboratory analysis
Figure 1. Typical Kamyr continuous digester [3] .
or an automatic device. So, long delays make it difficult to use feedback or feed forward control to change process conditions.
2.1. The Kappa Number
The main control variable in a Kamyr digester is the kappa number, which represents a reference to the amount of residual lignin in the pulp (and also a reference of leucochromophores groups). The primary control objective for the digester is to produce pulp at a specified Kappa range, thus producing pulp of steady quality. The steady blow line kappa number enables stability in the following parts of the fiber line. A high kappa number increases the bleaching chemicals cost. On the other hand, a low Kappa number means damaging the cellulose fibers (affecting pulp yield and strengths).
Controlling the digester is a difficult task because of the long time delays involved, non-linear behavior and infrequent availability of process measurements. In a general way, Kamyr digester chip level poses a difficult control problem, because the chip column dynamics are complex and it is difficult to measure the chip-liquor interface. A good control of the chip level is required to smooth digester operations [4] . If a disturbance affecting the Kappa number occurs, it will take at least one process dead time increased by the time required for analysis before the disturbance is detected.
In many digesters, the kappa number is measured off-line (although online analyzers are very common) using TAPPI T236-85 method [5] . An accurate dynamical model of the process can be very useful for predicting the future behavior of important process variables and can serve as the basis for developing an advanced control scheme. On the other hand the complexity and the high nonlinearity of the reactor makes it difficult to build models for estimating the kappa number in real time, using first principles or simple stochastic methods. An accurate model however would be very desirable, since it could serve either as an inferential sensor for the kappa number on-line estimation, or as the basis of a model-based control scheme.
2.2. Kraft Pulping Modeling
The Kraft pulping process for both batch and continuous digesters has been modeled to various levels of complexity. Optimal cooking conditions in the chip scale are well known. However, the usual problem is that the optimal conditions in the digester scale cannot be ensured. Large dimensions of the process equipment, difficult measurements and long residence time are the main reasons for this.
The development of rate expressions for Kraft pulping is complex by the heterogeneous nature of the system. A variety of factors affect the overall reaction rate, among them are thermal factors, fluid dynamic factors, diffusion characteristics of the liquor and chips, and the delignification reactions [6] . Modeling and simulation of pulping processes has been used for predictive analysis, configuration changes, process optimization by virtually changing combinations of process parameter settings, or simply for gaining better understanding of an existing process.
The industrial statistical models approach is timely dependent, since it can quantitatively identify the dyna- mics or physical properties of a process, using data obtained during actual production conditions. Different models control in kraft pulping are widely avalaible in the literature concerning to kappa number prediction. Among them, Alexandridis et al. [7] studied neural network methodology to develop a dynamic model for predicting kappa number either as inferential sensor or as a predictor of the future behavior of the process. Used data points from a Kamyr continuous digester, whit the objective to control the kappa number in a simulated continuous digester. Ahvenlampi and Kortela [8] studied a fuzzy clustering approach in the controllability of the kappa number. The results showed the usability of the combined hybrid system in the monitoring of the process and the kappa number prediction. Halmevaara and Hyotniem [9] developed a method using multivariate regression to capture the dependencies among the system parameters and quality measures of a double vessel continuous digester to softwood pulp through six operational variables of the digester.
The production of pulp for paper products has been a widely studied subject, especially concerning to softwood aspects, but few are the references to kappa number prediction techniques concerning to hardwood pulps.
3. Box & Jenkins Methodology
The ability to forecast optimally, to understand dynamic relationships between variable and to control optimally is of great practical importance. Much of statistical methodology is concerned with models in which the observations are assumed to vary independently. In many applications dependence between the observations is regarded as a nuisance, and in planned experiments, randomization of the experimental design is introduced to validate analysis conducted as if the observations were independent. However, a great deal of data in engineering and industries occur in the form of time series where observations are dependent and where the nature of this dependence is of interest in itself. The body of techniques available for the analysis of such series of dependent observations is called time analysis series (a set of observation generated sequentially in time), which may be classified as linear or nonlinear. Linear models are the most popular ones, due to their simplicity and ease of use. Examples of widely used linear methodologies are the Auto Regressive (AR) Moving Average (MA) models, which had been studied extensively by George Box and Gwilym Jenkins, and their names have frequently been used synonymously with general ARMA processes applied to time-series analysis, forecasting and control. The auto-regressive model specifies that the output variable depends linearly on its own previous values. The moving average specifies a dependence relationship among the successive error terms, which in this time-terminol- ogy should not be confused with the use of the same phrase in other statistical methods. The term “moving average” is used only in reference to a series of terms involving errors at different time periods. This general model uses an iterative three-stage modeling approach [10] :
Model identification and model selection: making sure that the variables are stationary, identifying seasonality in the dependent series (seasonally differencing it if necessary), and using plots of the autocorrelation and partial autocorrelation functions of the dependent time series to decide which (if any) autoregressive or moving average component should be used in the model.
Parameter estimation using computation algorithms to determine the coefficients that best fit the selected ARMA model.
Model checking by testing whether the estimated model conforms to the specifications of a stationary univariate process. In particular, the residuals should be independent of each other and constant in mean and variance over time. If the estimation is inadequate, it is necessary to return to the first step and attempt to build a better model.
After these steps, it is important to make a model validation.
Autoregressive (AR) models may be effectively coupled with moving average (MA) models to form a very general and useful class of stationary time-series models called autoregressive/moving average (ARMA) expressed by Equation (1), which may be easily included in any electronic spread sheet:
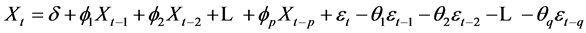 (1)
(1)
where:
Xt is the value of the output variable at time t;
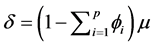 ; μ denoting the process mean;
; μ denoting the process mean;
 are the parameters of the AR model;
are the parameters of the AR model;
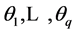 are the parameters of the MA model;
are the parameters of the MA model;
εt is the random error component at the time t.
The parameters of the model are estimated by least squares or the maximum likelihood statistical method [11] under the assumption of normal distribution for the random error component. Conditions on the parameters
 are required for proper estimation
are required for proper estimation
The input series for ARMA needs to be stationary (should have a constant mean, variance, and autocorrelation through time). In order to determine the stationarity, it is necessary to examine the plot of the data and autocorrelogram. Not only does the model have to be stationary, it also has to be invertible. There is a “duality” between the moving average process and the autoregressive process, the moving average equation above can be rewritten (inverted) into an autoregressive form (of infinite order). However, this can only be done if the moving average parameters follow certain conditions. Otherwise, the series will not be invertible [12] .
Most time series analysis consists of observations that are serially dependent in the sense that a model statistical with one or more parameters can be estimated to describe the relationship of consecutive observations and to forecast future values of the series from a specific time. In the recent years, the use of time series models for conducting forecasts in datasets has proved to be an important and reliable tool in several areas and research practice confirms its power and flexibility [13] [14] . Put into words, each observation of the series can be expressed as a random error component (εt) plus a linear combination of prior observations and prior random shocks.
4. Data Acquisition
Statistical modeling techniques were used to evaluate data generated from a eucalyptus Kraft pulp mill located at Minas Gerais state in Brazil. The equipment under study is a Kamyr single vessel vapor phase continuous digester in process of Extended Modified Continuous Cooking (EMCC) with a capacity of 500,000 admt/year. Data were collected under steady state operation over a period of 2 months totaling 2.306 observations that were divided into two data sets equally. The first was used as reference (to estimate the parameters of the model) and the second was used to validate the model. Some process variables contained occasional missing values and the corresponding data points in the input variables were removed. All the variables are relative to 30 minutes averages. To estimate the parameters, it was used the statistical software Eviews (Econometric Views) v.5 [15] .
5. Results and Discussion
Assumptions of normality, linearity, and homogeneity of variance were evaluated at building model data set. Models were evaluated according to different statistical decision criteria, like Mean Absolute Deviation (MAD), Mean Absolute Percent Error (MAPE), Rooted Mean Square Error (RMSE), Akaike Information Criterion (AIC), Schwarzs Bayesian Criterion (SBC), Durbin Watson (DW), R2 adjusted and Theil Inequality Coefficient (TIC). A discussion of the use of these and related scalar measures to choose between alternative models in a class, is available in different statistic books [10] [12] [13] .
In Figure 2 are presented the histogram and descriptive statistic of the standardized values of the Kappa number. Data were auto scaled to unit variance (i.e., each data were divided by its standard deviation) and mean centered. Assumption of normality is providing by large sample size and visual evidence of the graphic.
The study of residuals was considering in the choice of the models. It is very important for deciding on the appropriateness of a given forecasting model. If the errors are essentially random, the model may be a good one. If the errors show any type of pattern it is an indication that the model is not taking care of all the systematic information in the date set.
To identify the best model, were examined the autocorrelation and partial correlation of the kappa number data, and were observed significant autocorrelations (at 5% significance level) in the first 2 - 3 lags, and removal of the dependence on the intermediate observations (those within the lag).
According to some statistical decision criteria (AIC, SBC, TIC, RMSE, MAD and MAPE) presented in Figure 3 and Figure 4, the best forecasting model was the ARMA (1, 2). It’s estimated parameters are presented in Figure 4.
In Figure 4 are also presented the actual and forecasted kappa on each time t, calculated by parameters indicated according to preceded observations.
Histogram of the residuals (actual-estimated) and corresponding descriptive statistics data are shown in Figure 5.
Residuals autocorrelation and partial correlation are presented in Figure 6 adjusted for ARMA (1, 2), indicating a white noise and homoscedasticity of residuals.
Figure 2. Histogram and descriptive statistics of standardized Kappa number.
Figure 3. ARMA (1, 2) model estimated parameters.
Figure 4. ARMA (1,2) forecasting parameters.
Figure 5. Residuals histogram of ARMA (1, 2) model.
Figure 6. Residuals correlograms.
Considering accuracy and parsimony properties, the models ARMA (2, 1) ARMA (2, 2) and ARMA (1, 1) (in this order) showed good results according to the statistical decision criteria indicated at Table 1.
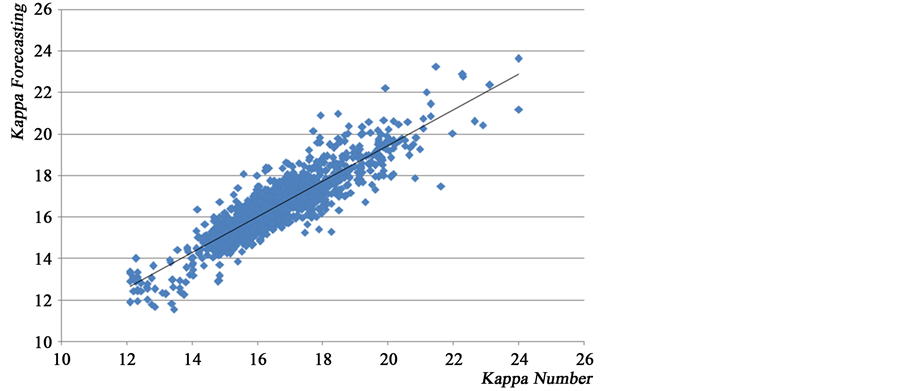
Applying coefficients indicated in Figure 3 at Equation (1), the second data set obtained from one month of the continuous digester operation were compared to the fitted model to perform the predictions. A value of MAPE around of 2.7% was obtained as can be seen at Table 2. A scatter graphic of observed/estimated kappa of model ARMA (1, 2) is shown in Figure 7 showing the good accuracy of the model.
Figure 7. Validation of model ARMA (1, 2) fitted for Kappa series.
Table 1. Results from the statistical criteria for approved models.
Table 2. Results from the statistical criteria for validation data.
6. Conclusion
In this paper we have shown general results concerning the performance of ARMA models for predicting the kappa number in continuous digester. Analysis of the generalized residuals and different statistical forecasting indexes indicates good fitting of three models by autoregressive and moving average parameters of order 1 and 2. From the results, it can be concluded that Box & Jenkins methodology was appropriated to predict the kappa number in continuous digester, being simple and easily implemented in any eletronic spreadsheet configuration.
References
- Box, G. and Jenkins, G. (1994) Time Series Analysis: Forecasting and Control. Holden-Day, San Francisco.
- Kokurek, M.J., Grace, T.M. and Malcom, E.W., Eds. (1989) Alkaline Pulping, Vol. 5 of Pulp and Paper Manufacture. 3th Edition, Joint Textbook Committee of the Paper Industry, Atlanta.
- Smook, G.A. (1988) Handbook for Pulp and Paper Technologists. TAPPI, Atlanta.
- Correia, F.M., Colodette, J.L., Regazzi, A.J. and Gomide, J.L. (2011) Eucalyptus Chip Compaction Disturbance Analysis in a Vapor Phase Continuous Digester. Proceedings of the 5th International Colloquium on Eucalyptus Kraft Pulp, P. Seguro, Brasil.
- TAPPI—Test methods (2001) TAPPI T 236 OM-06 Kappa Number of Pulp Atlanta, USA.
- Gullichsen and Fogelholm, Eds. (1999) Chemical Pulping: Vol. 5 of Papermaking Science and Technology Series. TAPPI Press, Atlanta.
- Alexandridis, A., Sarimveis, H., Bafas, G. and Retsina T. (2002) A Neural Network Approach for Modeling and Control of Continuous Digesters. TAPPI Fall Technical Conference, San Diego.
- Ahvenlampi, T. and Kortela, U. (2005) Clustering Algorithms in Process Monitoring and Control Application to Continuous Digesters. Informatica, 29, 101-109.
- Halmevaara, K. and Hyötyniemi, H. (2005) Performance Optimization of Large Control Systems—Case Study on a Continuous Pulp Digester. Proceedings of the 15th IFAC World Congress, Czech Republic.
- Makridakis, S.G., Wheelwright, S.C. and Hyndmann, R.J. (1998) Forecasting: Methods and Applications. 3th Edition, John Wiley and Sons, 642pp.
- Berkson, J. (1956) Estimation by Least Squares and by Maximum Likelihood. Proceedings of the Third Berkeley Symposium on Mathematical Statistics and Probability, Vol. 1: Contributions to the Theory of Statistics, 1-11. University of California Press, Berkeley. http://projecteuclid.org/download/pdf_1/euclid.bsmsp/1200501642
- Bowerman, B.L, O’Connell, R.T. and Koehler, A.B. (2005) Forecasting, Time Series, and Regression: An Applied Approach. 4th Edition, Duxbury Press, 686 p.
- Pankratz, A. (2009) Forecasting with Univariate Box-Jenkins Models: Concepts and Cases (Vol. 224). John Wiley & Sons, Hoboken.
- Tufa, L.D., Ramasamy, M., Patwardhan, S.C. and Shuhaimi, M. (2010) Development of Box-Jenkins Type Time Series Models by Combining Conventional and Orthonormal Basis Filter Approaches. Journal of Process Control, 20, 108-120.
- www.eviews.com
NOTES
*Corresponding author.