Journal of Biomaterials and Nanobiotechnology
Vol.3 No.1(2012), Article ID:16700,9 pages DOI:10.4236/jbnb.2012.31014
Measurements of Heat Treatment Effects on Bovine Cortical Bones by Nanoindentation and Compression Testing
![]()
1Centre of Excellence in Engineered Fibre Composites, Faculty of Engineering and Surveying, University of Southern Queensland, Toowoomba, Australia; 2Department of Mechanical Engineering, The Hong Kong Polytechnic University, Hong Kong, China; 3Centre for Advanced Composite Materials, Department of Mechanical Engineering, The University of Auckland, Auckland, New Zealand; 4Department of Applied Biology and Chemical Technology, The Hong Kong Polytechnic University, Hong Kong, China.
Email: {MeiLing.Lau, *Kin-tak.Lau}@usq.edu.au
Received October 19th, 2011; revised November 22nd, 2011; accepted December 16th, 2011
Keywords: Bone; Heat Treatment; Nanoindentation; Mechanical Properties; BSE and EDX
ABSTRACT
Heat treatment of bone is one of the reliable and simple sterilization methods to overcome the risk of rejection and disease transfer from allograft and xenograft, in particular for the prevention of human immunodeficiency virus (HIV) infection. However, the mechanical property of the micro-structural level after heat treatment is not well characterized. To address this issue, this study was carried out to compare the localized mechanical properties of micro-structural tissue with those at the global structural level. Nanoindentation technique has been well accepted as an accurate technique to measure mechanical property of small and heterogeneous specimen nondestructively, as well as the complex bio-material of micro-structural level, often with a resolution of better than 1 mm. In this study, nanoindentation was conducted to measure the localised elastic modulus and hardness values of bones at temperature of 23˚C (room temperature – nonheated sample), 90˚C and 150˚C, respectively. All experiments were conducted at room temperature (~23˚C). The elastic modulus (E) and nanoindentation hardenss (H) values in the longitudinal direction of bones heated at 150˚C were recorded as 23.43 GPa and 0.73 GPa, respectively; as in transverse direction, the E and H values were 12.77 GPa and 0.54 GPa, respectively. It showed significant increases of 44% and 43% in the longitudinal direction as compared to those of the non heat-treated bones. In addition, E and H values in transverse direction also showed increases of 23% and 38%, respectively as compared to those of the non heat-treated bones. Furthermore, heat-treated bones at 90˚C in longitudinal direction also appeared to have significant increases of 18% and 31% in E and H values, respectively. However, the E and H values in transverse direction increase only by 0.4% and 12.8%, respectively. In addition, compressive test is employed to measure the global stiffness (E) of the bone samples. When heated at 150˚C, the bone specimen showed an increase of 60% in stiffness (E) and an increase of 26% in yield stress. On the other hand, when heated at 90˚C, a slight increase of 11.4% in stiffness (E) and 21.5% in yield stress were recorded respectively. Furthermore, energy dispersive X-ray spectroscopy (EDX) which integrated with Backscattered Electron (BSE) imaging was conducted to examine the relationship between mineral content and mechanical strength within the nanoindentation regions. The data demonstrated that the non heat-treated bones obtained the highest calcium wt% amongst the three groups; as temperature increased, there was a slight decrease in calcium wt%; however, the changes were not severe in this study.
1. Introduction
Autografts are commonly used for human bone replacement; however, they are limited in volume and additional surgery is needed [1]. In the last decade, heat-treated cortical bone has been proposed as a substitute for bone transplant material to overcome the risks of rejection and disease transfer from allograft and xenograft [2]. With advantages obtained in biological and mechanical properties, it is believed that heat-treated bones can be excellent alternative material for bone grafts and synthetic bone substitutes. Extensive research has been conducted in the past decade to study the structural arrangements, material compositions and mechanical properties of bone [1-10] in order to understand the bone problems such as bone fracture. Bone remodeling and the design of bone-implant system have also been carried out. Various methods have been used to visualise the internal architecture of the cancellous bone to create in vivo images of whole bone, such as quantitative computed tomography (QCT) and magnetic resonance (MR) [11]. With the combination of finite element (FE) modelling, the elastic and failure properties of the cancellous bone can be quantified directly from the high-resolution images of the QCT and MR [11-14]; mechanical testing [1,2,15-17] and nanoindentation testing [18-23] are used to measure the elastic modulus and hardness of cortical and cancellous bone.
Apart from the study of the structural and mechanical properties, a number of experiments have been focused in investigating the effect of mineral content after heat treatment. As described by Todoh et al. [24], the mineral inside the bone controls its stiffness and strength, while the collagen matrix controls the toughness, viscoelasticity and tensile strength. Therefore, the degeneration of mineral content and collagen matrix would affect the bone’s mechanical properties. Todoh et al. [24] have also reported that the Young’s modulus of cortical bone along the bone axis, after degeneration at 200˚C, to be about 12 GPa (using the four-point bending test), whereas that of the intact specimen was 20 GPa. The tensile strength of the degenerated specimen was 38 MPa as compared to 178 MPa for the intact specimen. However, a contradictory result was obtained by Catanese III et al. [1]: the elastic modulus remained similar to that of an intact cortical bone along the bone axis, being 16.3 ± 2.2 GPa for compression and 16.3 ± 3.7 GPa for tension when a cortical bone was heated up to 350˚C. In addition, the cortical bone was found to have maintained 63% of its intact strength in compression after being heated up to 350˚C, making it well suited for compressive load-bearing applications as mentioned by Catanese III et al. [1].
Nanoindentation testing is one of the promising novel techniques recently used to quantify the mechanical properties of microstructures of various materials. This technique evolves from conventional Vickers microhardness testing, with additional capability of making small indentations at precise positions on microstructural features, while concurrently monitoring the loads and displacements of the indenter on the specimen surface. The nanoindentation is well suited to examine the microstructual features of material surface to provide a spatial resolution which is less than 1 mm [9,10,20,25]. Since bone tissues varies at different structural levels (from microsturcture of 10 to 500 mm to sub-nanostructure of 1 nm) [3], the mechaniccal properties of microstructural units of bone tissues down to the osteon level can be explored by using nanoindentation technique. By analyzing the indentation load-displacement behaviour, it is possible to obtain the measurements of the Young’s modulus, E, and hardness, H, of the bone [1,9,19,23]. Rho et al. [20] have employed the nanoindentaion technique to indirectly measure the Young’s modulus of bone through the observation of the return path of the load-displacement curve. It has been reported that the Young’s modulus, measured in the longitudinal direction are 22.5 ± 1.3 GPa for the osteons and 25.8 ± 0.7 GPa for the interstitial lamellae. Higher elastic moduli of 24.7 ± 2.5 GPa and 30.1 ± 2.4 GPa, for the osteons and the interstitial lamellae of cortical bone in the longitudinal direction, respectively, have also been reported by Wang et al. [19]. In addition, the hardness values of the cortical bone in the longitudinal direction ranging from 0.81 to 0.89 GPa for the osteons and the interstitial lamellae were also reported by Wang et al. [19].
The goal of this study is to employ surface nanoindentation to localize the mechanical properties, both elastic moduli and hardness values of different heat-treated bovine cortical bones in longitudinal and transverse directions. In addition, compressive test is employed to characterize the global elastic modulus of bone specimens in longitudinal direction. This research also represents an attempt to understand the correlation between mineral content and the mechanical strength by backscattered electron (BSE) imaging.
2. Materials and Methods
2.1. Sample Preparation for Nano-Indentation Test and BSE Imaging
An experimental study was conducted to examine the mechanical properties of non-heated and pre-heated bovine cortical bones through nanoindentation. Three specimens of rib from a fresh frozen bovine were machined into 5 mm thickness along its transverse plane, and another three specimens were sectioned into 3 mm thickness along its longitudinal plane by a low-speed diamond saw (Metkon, resin bonded diamond cut-off wheels) under constant water application. A soft water jet was used to remove marrow inside the specimens. All the specimens were then placed into an ultrasonic bath to remove surface debris. Six specimens were equally divided into three groups. All specimens were prepared promptly after sacrifice within 12 hours in order to obtain a more accurate result and eliminate the effects induced by chemical fixation. According to Currey et al. [26], the use of aldehydes can alter the mechanical properties of bones due to the fact that chemical fixation has a direct effect on the polypeptide collagen chains.
Bone specimens in Group 1 were dried naturally at room temperature and non-heat treated as a control group, whereas Groups 2 and 3 were dried and heat-treated at pre-set temperatures in an oven, the details are as follows:
Group 1: Dried at room temperature (~23˚C) for 24 hours and embedded inside epoxy resin to provide support and allowed to cure over night at room temperature (~23˚C).
Group 2: Heat-treated at 90˚C for 2 hours and embedded inside epoxy resin to provide support and allowed to cure overnight at room temperature (~23˚C).
Group 3: Heat-treated at 150˚C for 2 hours and embedded inside epoxy resin to provide support and allowed to cure overnight at room temperature (~23˚C).
The reason to divide the specimens into non-heat treated and heat treated groups are to investigate the mechanical properties difference between these groups. These temperature ranges were selected for this study because it has been reported that non-calcified collagen of bone collagen molecules denature at about 60˚C and about 150˚C for the calcified collagen [24,27] while the heat treatment time setting was according to Todoh et al. as reference [24]. The temperature in the oven was programmed to desire range until it is stable for heat-treated the specimens. After cooling down for 12 hours, the bone specimens were embedded without being vacuumed into epoxy resin to provide support and allowed to cure for 24 hours at room temperature. Since only Araldite GY251 epoxy resin (with hardener HY956 mixture ratio of 5:1) was used to provide support for the bone specimens, there was, no need to use vacuum container to remove excessive bubbles that were induced by mixing the epoxy and hardener. Fan et al. [28] and Hoffler et al. [29] have stated that the employment of epoxy resin, as a support of bone only pervades into trabecular pores but not the tissue, thus, minimally influencing the nanoindentation results. All the indentations were performed away from the bone and resin boundary to improve data accuracy.
To minimize the confounding effect of surface roughness on nanoindentation properties, all the specimen surfaces were finely polished before the nanoindentation tests. The specimens were grounded by different grades of silicon carbide papers (60, 320, 800, 1200 and 2000 grits) under soft water jet and then further polished manually by soft synthetic flock polishing cloths with different grades of the diamond powder (15 mm, 6 mm and 1 mm). After grinding and polishing, the specimens were washed by distilled water to clean up the surface debris. In order to obtain a clear lamellar microstructure of the bone as shown in Figure 1, all the specimen preparations were confirmed under an optical microscope to obtain a smooth surface for indentation.
Same groups of bovine specimens were used for BSE imaging. After the nanoindention test, the surfaces of bovine cortical specimens in the longitudinal direction were coated in a thin layer of carbon by vacuum evaporation, the used of carbon instead of coated with gold because the images are more clear and furthermore, the coating method was according to Roschger et al. [30] as reference.
2.2. Sample Preparation for Compression Test
For the compressive test, additional 9 specimens of rib cut in the longitudinal direction were machined and divided into 3 groups, the cross sectional dimensions were approximately 1.2 × 2.6 mm with 1 mm height. Bone specimens in Group 1 were non-heated as a control group, whereas Groups 2 and 3 were heat-treated at pre-set temperatures in an oven at 90˚C and 150˚C, respectively. The preparation procedures were the same as that for nanoindentation test but without embedding the specimens into epoxy in order to avoid any inaccurate result.
2.3. Nanoindentation Test
A scanning nanoindenter (TriboScratch; Hysitron, Inc., Minneapolis, USA) comprised of a scanning probe microscope and a nanoindentation transducer was used at room temperature (~23˚C) throughout the experimental study. A sharp Berkovich (three-sided pyramid) diamond indenter tip was embedded in the transducer to measure the nanoindentation modulus and hardness. The experimental specimen was glued on a stainless steel stage and the microstructure to be indented was located under the indenter with an optical microscope for continuous monitoring of the loads and indenter displacements. By using the x-y table and z height, the small indentations could be precisely positioned on the specimen surface with constant loading and displacement rate. Note that the working distance between the indenter and specimen was retained constant throughout the test.
At the start of the test, the Berkovich indenter tip was slowly driven towards the specimen surface at a constant displacement rate and a permanent hardness impression was made after the surface contact. A maximum load of 30 mN with a loading and unloading rate of 0.3 mN/s produced a surface contact depth of 1000 nm and the hardness impression was held for a period of 5 s at the maximum load to eliminate any creep behaviour. The data obtained from indentation load-displacement test were analysed to calculate the elastic modulus, E, and the hardness, H, using the method of Oliver and Pharr, where the indenter area function has been well documented [31]. This method is based on the measurement of the contact stiffness S, from the upper portion of the unloading data to determine the relationship between contact stiffness and the elastic properties of the specimen.

Figure 1. (a) A total of 75 indentations were produced in the longitudinal direction of non-heat treated bovine cortical bones; (b) A total of 118 indentations were produced in the transverse direction of non-heat treated bovine cortical bones.
In the upper portion of the initial unloading, the contact stiffness S is defined as,
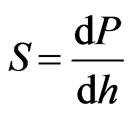 (1)
(1)
The relationship between contact stiffness and the elastic properties of the specimen is given by
 (2)
(2)
where P is the load, h is the depth, 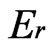 is the reduced modulus, and A is the projected area of the elastic contact. The reduced modulus is related to the elastic modulus, E as per Equation (3)
is the reduced modulus, and A is the projected area of the elastic contact. The reduced modulus is related to the elastic modulus, E as per Equation (3)
 (3)
(3)
where, 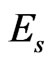 and
and 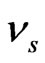 are the elastic modulus and Poisson’s ratio for the specimen, respectively and
are the elastic modulus and Poisson’s ratio for the specimen, respectively and 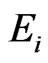 and
and 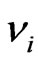 are the same parameters for the indenter. For a standard diamond indentor probe,
are the same parameters for the indenter. For a standard diamond indentor probe, 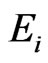 is 1140 GPa and
is 1140 GPa and 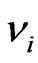 is 0.07. Bone has been assumed to be isotropic, elasto-plastic material; thus, the Poisson’s ratio
is 0.07. Bone has been assumed to be isotropic, elasto-plastic material; thus, the Poisson’s ratio 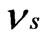 may be taken as 0.3. As mentioned by Rho et al. [8], the change of measured value of
may be taken as 0.3. As mentioned by Rho et al. [8], the change of measured value of 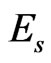 should not excess 8% while
should not excess 8% while  ranged from 0.2 to 0.4.
ranged from 0.2 to 0.4.
The elastic modulus is derived by measuring the initial unloading stiffness and assuming that the contact area is equal to the optically measured area of the hardness impression. The hardness, H, is calculated as:
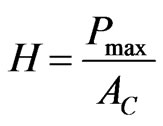 (4)
(4)
where, Pmax is the maximum indentation force, 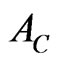 is the projected contact area.
is the projected contact area.
2.4. Mechanical Properties Measured by Compressive Tests
The compressive test was performed on an axial static testing (RT/50(50kN), MTS Corp., Eden Prairie, Minnesota). The specimen was aligned in its bone axis and placed between two parallel stainless steel platens. The compressive strengths of all specimens were tested to failure at a compression speed of 0.4 mm/s. Stress was determined from the measured applied force (P) divided by the crosssectional area (A), (σ = P/A) whereas, strain (e) was measured as length elongation (δ divided by the original specimen length (L0). A program was created to obtain the data and an excel file was used to plot the stress vs strain curve, thus, the elastic modulus or Young’s modulus (E = σ/e) was generated from the slope of the stress-strain curve in the elastic region. Since it is often difficult to pinpoint the exact stress at which plastic deformation begins, the yield stress is often taken to be the stress needed to induce a specific amount of permanent strain, typically 0.2% [32].
2.5. Examination of Mineral Content by BSE Imaging
BSE imaging (Scanning Electron Microscope, Leica Stereoscan 440) was operated with the accelerating voltage of 20 kV at a working distance of 10 mm to capture the images. Backscattered electrons were obtained by a detector that reflected back the high-energy electrons after they collided on the specimen surface. The BSE signal was then converted into grey-scale images by analysing the contrast of the images; it allowed the determination of chemical compositions and distribution in the samples [30].
3. Results
3.1. Nanoindentation Results
In total, 642 indentations were made within osteons and nearby interstitial regions of cortical bone along the longitudinal direction. However, due to the structural arrangements of lamella, it is difficult to distinguish osteons and the interstitial regions in transverse direction, therefore, the indentation sites were ramdonly chosen, and the elastic modulus in transverse direction was the mean of the osteons and interstitial regions. Lamella is defined as the submicrostructure level according to Rho et al. [3]. Three groups of elastic modulus (E) and hardness (H) measurements of the bovine cortical bones in longitudinal and transverse directions were obtained through load-displacement curves as shown in Figure 2, indicating the response of osteons varied with direction. For Group 1, a total of 75 indentations, as shown in Figure 1(a), were produced in the longitudinal direction, the average Young’s modulus (E) in longitudinal direction was 16.23 GPa, and the average hardness value (H) was 0.51 GPa, whereas, 118 indentations as shown in Figure 1(b) produced in the transverse direction, gave the average values of E and H as 10.38

Figure 2. Load-displacement curve of heat-treated bone at 90˚C. S is the contact stiffness, P is the applied load and h is the depth. S is the slope of the initial portion of unloading curve.
GPa and 0.39 GPa, respectively. The average Young’s modulus and hardness values for heat-treated (90˚C and 150˚C) specimens (Groups 2 and 3), calculated from a number of indentations, are summarised in Table 1.
The nanoindentation experimental data showed significant increases of 44% and 43% in E and H values, respectively in longitudinal direction when bones were heated at 150˚C as compared to those of the non-heat treated bones. In addition, E and H values in transverse direction also showed increases of 23% and 38%, respectively at 150˚C as compared to their counter parts. Furthermore, heat-treated bones at 90˚C in the longitudinal direction appeared to have significant increases of 18% and 31% in E and H values, respectively. However, heat-treated bones at 90˚C appeared not to increase as much in the transverse direction, increasing by only 0.4% and 12.8% in E and H values, respectively.
3.2. Compressive Test Results
The differences in the elastic properties of the non-heated and heat-treated samples were analysed using one-way analysis of variance (ANOVA). The elastic modulus (obtained from the linear portion of the stress-strain curve) of the bovine bone varies with the increase of heating temperature as shown in Table 2. The compressive modulus of Group 1 specimen is 3.5 ± 0.6 GPa, whereas, the moduli of Group 2 and 3 are 3.9 ± 0.44 GPa and 5.6 ± 0.48 GPa respectively. The bone specimen, heat-treated at 90˚C
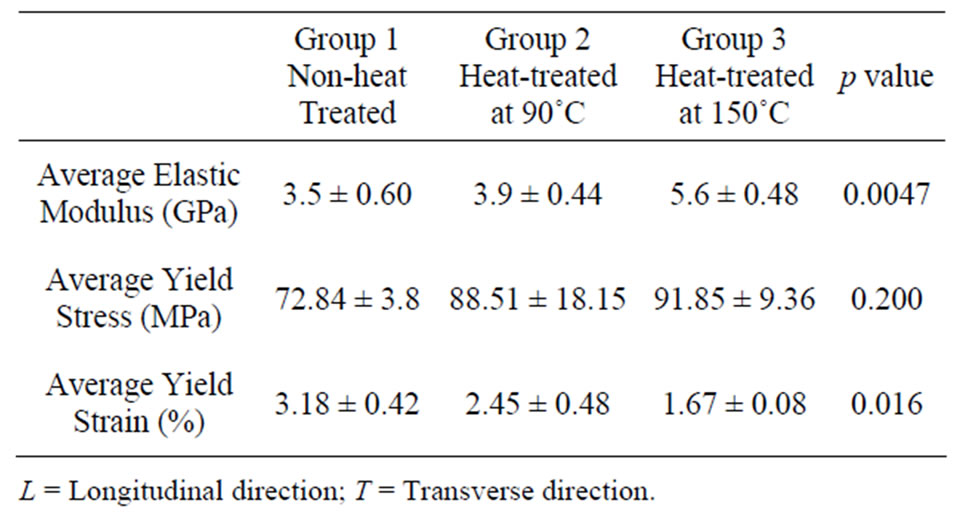
Table 1. Average elastic moduli and hardness values of bovine cortical bone in various temperatures.
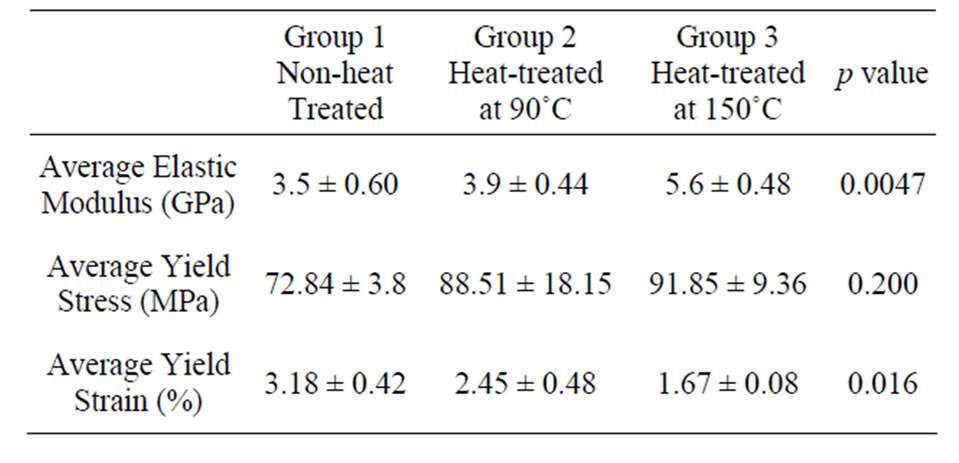
Table 2. Average elastic moduli, yield stress and yield strain of cortical bovine bone in various temperatures.
shows a slight increase of 11.4% in stiffness (E). In addition, a significant increase of 60% in stiffness (E) is obtained in bone specimen heat-treated at 150˚C. The yield stress and yield strain for heat-treated (90˚C and 150˚C) specimens (Groups 2 and 3), are also shown in Table 2. Figure 3 shows the typical stress strain curve of the nontreated group bovine specimen. Whereas Figure 4 shows the Young’s modulus and yield stress (σy) vs heating temperature.
3.3. Backscattered Electron (BSE) Imaging
Results
Six sites within the indentation regions were scanned and the indentation marks can be seen clearly in Figure 5. By visual examination of the BSE images, it was observed that the light gray regions corresponded to the tissues with higher mineral content and dark gray regions had lower mineral content. The imaged results were consistent with those of Hoc et al. [10], Roschger et al. [30] and Bloebaum et al. [33]—the local variation of mineral content can be quantified by the frequency distribution of gray levels.
In addition, energy dispersive X-ray spectroscopy (EDX) was performed to further examine the weight percentages of calcium and phosphorous in each site. EDX measurements were used to conduct Ca/P molar ratios, which confirmed the compositional differences among three groups of specimens in Table 3. The data demonstrate that the non heat-treated bones has the highest (66.6%) weight percentage (wt%) of calcium amongst the three groups. As the bovine bones are heat-treated, the wt% of calcium has a slight decrease. Heat-treated bovine cortical bones at 90˚C contain 65% of wt% of calcium on average (a decrease of 2.5%). In addition, the average wt% of calcium of heat-treated bovine cortical bones at 150˚C is 62.9%, indicating a higher decrease of around 5.6% compared to the non-heated group.
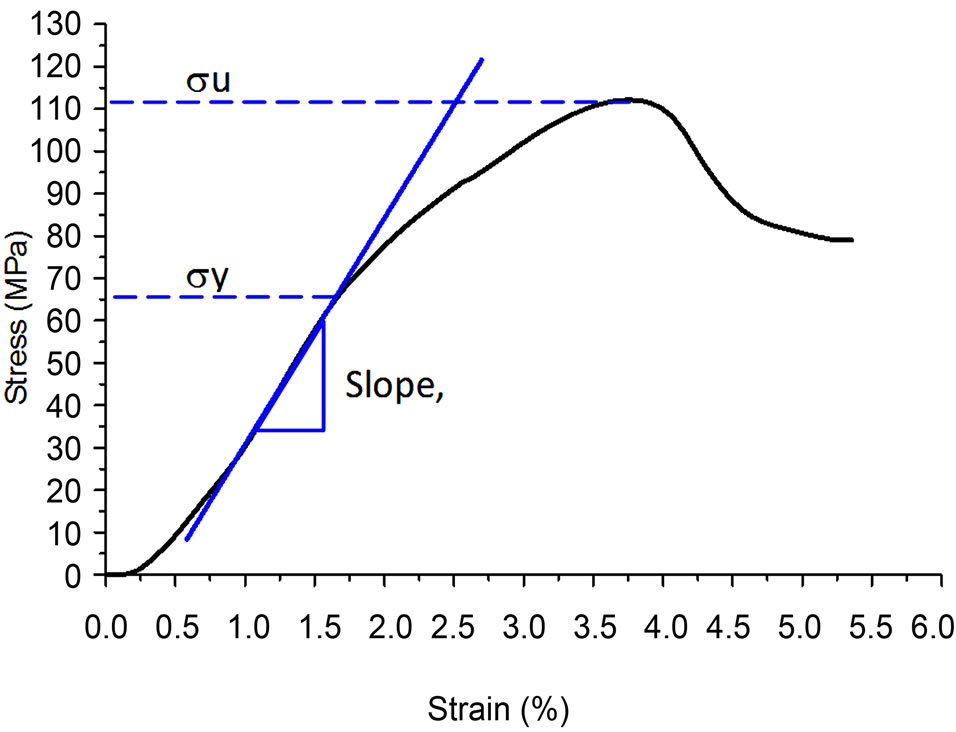
Figure 3. Stress-strain curve of heat-treated bone at 90˚C.
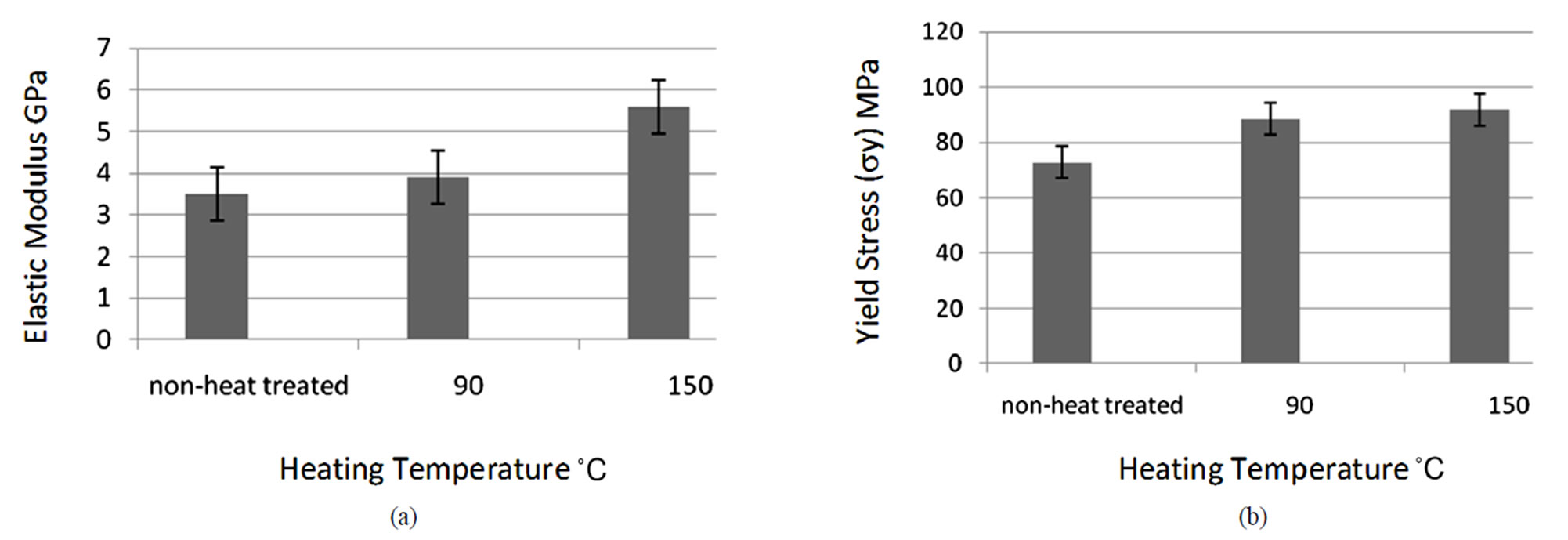
Figure 4. Compressive test results for mechanical properties: (a) Young’s modulus vs heating temperature; (b) Yield stress (sy) vs heating temperature.

Figure 5. Backscattered scanning electron (BSE) images of bovine cortical bone. Light and dark gray regions represent the higher and lower mineral contents, respectively.
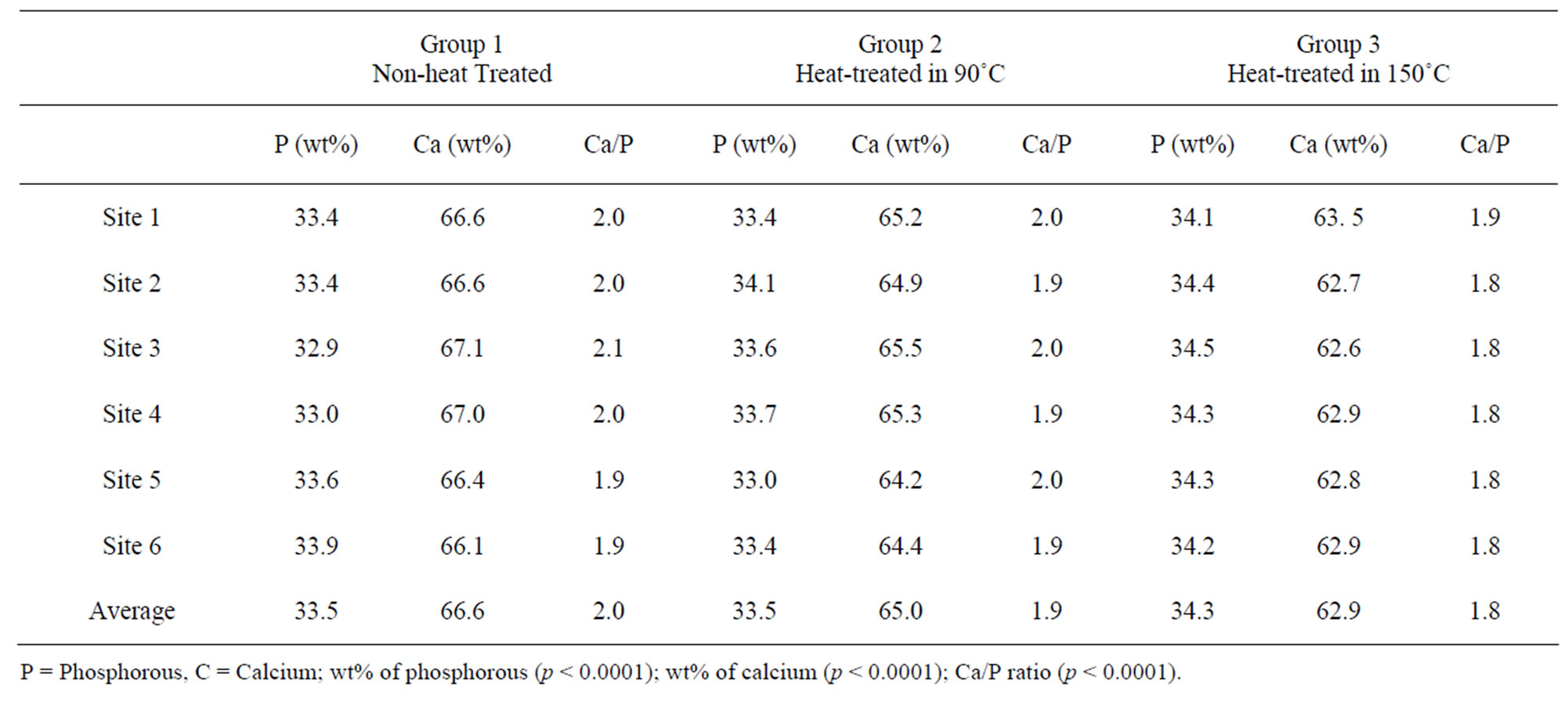
Table 3. Average weight percentage of calcium and phosphorous.
4. Discussion
A number of attempts have been made in the past few years to examine the mineral contents of bones after heat treatment, owing to the fact that the degeneration of mineral content is correlated to the strength of a bone [1,2,24,27,34]. In addition, collective evidence shows that a heat-treated bone could be one of the excellent substitutes for bone transplantation, apart from alleviating the risks of rejecttion and disease transfer from allografts and xenografts in implantation of bone, [1]. Heat-treated bone can also maintain desirable biological and mechanical properties. Shin et al. have reported that heat treatment can be a simple and practical way for clinical use in hospital to lower the infection of HIV as compared to gamma-irradiation or the use of ethylene oxide gas [2].
This study has demonstrated the localized properties of cortical bovine bones, both Young’s modulus (E) and hardness value (H), vary with heating temperatures applied to the bones and the orientation (the longitudinal and transverse directions) of the bones. In the longitudinal direction, the E and H values are generally much higher than those in the transverse direction at any heat treatment temperature reported in this study. This finding shows that the structural orientation of the collagen network has a significant influence on the mechanical properties of bone. According to Zioupos et al. [35] and Wang et al. [36], collagen parameters are correlated to toughness values and bone strength but have no significant impact on bone stiffness. Although it has been reported that collagen molecules may denature at about 43˚C for non-calcified collagen, and about 150˚C for the calcified collagen [27], the elastic modulus (E) does not change significantly. The result of nanoindentation technique has demonstrated that heat-treated cortical bones can maintain relatively high elastic moduli and hardness values at 90˚C and 150˚C as compared to those of the non-treated bones. The results also agree well with the findings of Catanese III et al. [1], who reported that the cortical bones heated up to 350˚C still maintained 63% of the elastic strength in compression compared to that of the untreated bones. They suggested that heat-treated bones at 350˚C could still be an excellent compressive load-bearing substitute in a human body.
In order to further investigate the global mechanical properties of bovine bone, compressive tests were conducted to measure the load-bearing ability of the specimen. It is interesting to note that the elastic modulus (E) of bone specimen in the compressive tests appear to have changed as much as those of the localized mechanical properties in the nanoindentation tests, thus indicating the resistance to deformation in heat-treated bovine specimens to be higher than that of the non-heated bones. Although the impact on stiffness is limited, the increased temperature might render the bones more brittle. Various researchers have reported that the variation in bone strength is related to the change of bone collagen [2,24,27]. Wang et al. [27] had stated that, the collagen molecules structure would be irreversibly changed (eg. unwinding of the triple helix) at specific temperature (over 150˚C), which play an important role in the fracture properties of bone. In addition, Shin et al. [2] have also reported that the degeneration of collagen most likely would affect bone strength against torsion rather than compression.
About 70% of bone tissues by weight are composed of inorganic components (mainly calcium and phosphorous crystals) which provide compression load-bearing properties and stiffness. In this study, BSE imaging was used to examine the correlation between Young’s modulus and the mineral content after heating. The lighter gray BSE images appear to have higher mineral contents than those of the darker ones. In addition, the weight percentages of calcium and phosphorous in Group 3 show a slight decrease as temperature increased. Although this slight change might be due to the local variations of mineral contents of a bone specimen, it also revealed that a lower mineral content exists in the BSE imaged region. A big loss of calcium can make it difficult to maintain higher toughness and stiffness in bones to withstand compression and bending. As stated by Bloebaum et al. [33] and Rho et al. [37], mineral content is a significant contributing factor to bone stiffness and strength. However, in this study, the changes were not severe (with P content increasing and Ca/P ratio decreasing) and the measurements were localized. Therefore the overall effects of these changes on the properties appear to be not as significant as other parameters. Several other parameters, such as the porosity, cross sectional area of cortical bone and lamina orientation at different treated temperatures are likely to play important roles in varying degrees for determining the bone properties.
There are several limitations that influence to this study: first, heat induced changes in the collagen fiber should involve other testing procedures, in particular for measuring the degeneration of the collagen molecules. In addition, according to various researchers [27,35,36], the degeneration of collagen fiber may not be the only factor causing the deterioration of bone strength and toughness. Secondly, EDX is one of the imaging methods to assess the weight percentages of calcium and phosphorous, but according to Raspanti et al. [38], the mineral phase structure of the bovine cortical bone remains unaffected when heated up to 500˚C. However, contrary to this, Holden et al. [39] have found that as temperature exceeds 400˚C, the mineral phase of human bone has significant changes, which can probably affect the bone stiffness and strength. Finally, different anatomical regions lead to the measured differences in results. As reported by Zysset et al. [22], the turnover rate and osteon type are distinctive to different anatomical locations: higher turnover rate means the reduced the mean age of osteons and lower mineralisation. Thus, larger sample size in various regions and various pre-heated temperatures are needed to enhance the accuracy of the results.
5. Conclusion
This paper presents the mechanical properties of bovine cortical bones in different directions under varying pretreating temperatures. The nano-indentation results present generally a higher Young’s modulus and hardness value in the heat-treated (at 90˚C and 150˚C) bones compared to those of the non-heated bones. This opens a scope for heat-treated bones to be a good bone graft substitutes with reduced risk of rejection and disease transfer. The compressive test results also agree with the nano-indentation results and it is found that as temperature increases the bone still maintains a higher elastic strength compared to the non-treated bones. The BSE imaging and EDX reveal only a slight decrease in calcium, thus, the increase in temperature appears not to be significant for the change in mineral content. In conclusion, heat treatment at both 90˚C and 150˚C are deemed to be acceptable, from the biological and biomechanical points of view. However, for bone grafting the ultimate clinical decision regarding the usage of heat-treated bones have to be made after considering other non-mechanical factors.
6. Acknowledgements
This project is supported by The Hong Kong Polytechnic University Grant and Research Grant Council (PolyU5198/ 07E-B-Q084) and the Centre of Excellence in Engineered Fibre Composites, The University of Southern Queensland, Australia.
REFERENCES
- J. Catanese III, J. D. Featherstone and T. M. Keaveny, “Characterization of the mechanical and ultrastructural properties of heat-treated cortical bone for use as a bone substitute,” Journal of Biomedical Meterials Research, Vol. 45, No. 4, 1999, pp. 327-336. doi:10.1002/(SICI)1097-4636(19990615)45:4<327::AID-JBM7>3.0.CO;2-L
- S. Shin, H. Yano, T. Fukunaga, S. Ikebe, K. Shimizu, N. Kaku, H. Nagatomi and S. Masumi, “Biomechanical properties of heat-treated bone grafts,” Archives of Orthopaedic and Trauma Surgery, Vol. 125, No. 1, 2005, pp. 1-5. doi:10.1007/s00402-004-0746-6
- J. Y. Rho, L. Kuhn-Spearing and P. Zioupos, “Mechanical properties and the hierarchical structure of bone,” Medical Engineering and Physics, Vol. 20, No. 2, 1998, pp. 92-102. doi:10.1016/S1350-4533(98)00007-1
- A. Stanishevsky, S. Chowdhury, P. Chinoda and V. Thomas, “Hydroxyapatite nanoparticle loaded collagen fiber composites: Microarchitecture and nanoindentation study,” Journal of Biomedical Meterials Research, Vol. 86A, No. 4, 2008, pp. 873-882. doi:10.1002/jbm.a.31657
- F. Ferreira, M. A. Vaz and J. A. Simões, “Mechanical Properties of bovine cortical bone at high strain rate,” Material Characterization, Vol. 57, No. 2, 2006, pp. 71-79. doi:10.1016/j.matchar.2005.11.023
- A. Tatarinov, N. Sarvazyan and A. Sarvazyan, “Use of multiple acoustic wave modes for assessment of long bones: Model study,” Ultrasonics, Vol. 43, No. 8, 2005, pp. 672-680. doi:10.1016/j.ultras.2005.03.004
- T. Jämsä, J. Y. Rho, Z. Fan, C. A. MacKay, S. C. Marks Jr. and J. Tuukkanen, “Mechanical properties in long bones of rat osteopetrotic mutations,” Journal of Biomechanics, Vol. 35, No. 2, 2000, pp. 161-165. doi:10.1016/S0021-9290(01)00203-2
- Z. Fan, P. A. Smith, E. C. Eckstein and G. F. Harris, “Mechanical properties of OI type III bone tissue measured by nanoindentation,” Journal of Biomedical Meterials Research, Vol. 79A, No. 1, 2006, pp. 71-77. doi:10.1002/jbm.a.30713
- J. Y. Rho and G. M. Pharr, “Effects of drying on the Mechanical properties of bovine femur measured by nanoindentation,” Journal of Materials Science: Materials in Medicine, Vol. 10, No. 8, 1999, pp. 485-488. doi:10.1023/A:1008901109705
- T. Hoc, L. Henry, M. Verdier, D. Aubry, L. Sedel and A. Meunier, “Effect of microstructure on the mechanical properties of Haversian cortical bone,” Bone, Vol. 38, No. 4, 2006, pp. 466-474. doi:10.1016/j.bone.2005.09.017
- B. van Rietbergen, S. Majumdar, W. Pistoia, D. C. Newitt, M. Kothari, A. Laib and P. Rüegsegger, “Assessment of cancellous bone mechanical properties from micro-FE models based on micro-CT, pQCT and MR images,” Technology and Health Care, Vol. 6, No. 5-6, 1998, pp. 413-420.
- A. Ural and D. Vashishth, “Cohesive finite element modeling of age-related toughness loss in human Cortical bone,” Journal of Biomechanics, Vol. 39, No. 16, 2006, pp. 2974-2982. doi:10.1016/j.jbiomech.2005.10.018
- A. Ural and D. Vashishth, “Anisotropy of age-related toughness loss in human cortical bone: A finite element study,” Journal of Biomechanics, Vol. 40, No. 7, 2007, pp. 1606-1614. doi:10.1016/j.jbiomech.2006.07.023
- Z. Fan, J. Y. Rho and J. G. Swadener, “Three-dimensional finite element analysis of the effects of anisotropy on bone mechanical properties measured by nanoindentation,” Journal of Meterials Research, Vol. 19, No. 1: 2004, pp. 114-122. doi:10.1557/jmr.2004.19.1.114
- S. M. Bowman, J. Zeind, L. J. Gibson, W. C. Hayes and T. A. McMahon, “The Tensile Behavior of Demineralized Bovine Cortical Bone,” Journal of Biomechanics, Vol. 29, No. 11, 1996, pp. 1497-1501. doi:10.1016/0021-9290(96)84546-5
- S. P. Kotha and N. Guzelsu, “Tensile behavior of cortical bone: Dependence of organic matrix material properties on bone mineral content,” Journal of Biomechanics, Vol. 40, No. 1, 2007, pp. 36-45. doi:10.1016/j.jbiomech.2005.11.016
- J. D. Currey, “The Effect of Porosity and Mineral Content on the Young’s Modulus of Elasticity of Compact Bone,” Journal of Biomechanics, Vol. 21, No. 2, 1988, pp. 131- 139. doi:10.1016/0021-9290(88)90006-1
- C. H. Turner, J. Y. Rho, Y. Takano, T. Y. Tsui and G. M. Pharr, “The Elastic Properties of Trabecular and Cortical Bone Tissues Are Similar: Results from Two Microscopic Measurement Techniques,” Journal of Biomechanics, Vol. 32, No. 4, 1999, pp. 437-441. doi:10.1016/S0021-9290(98)00177-8
- X. J. Wang, X. B. Chen, P. D. Hodgson and C. E. Wen, “Elastic modulus and hardness of cortical and trabecular bovine bone measured by nanoindentation,” Transactions of Nonferrous Metals Society China, Vol. 16, No. 2, 2006, pp. s744-s748. doi:10.1016/S1003-6326(06)60293-8
- J. Y. Rho, T. Y. Tsui and G. M. Pharr, “Elastic properties of human cortical and trabecular lamellar bone measured by nanoindentation,” Biomaterials, Vol. 18, No. 20, 1997, pp. 1325-1330. doi:10.1016/S0142-9612(97)00073-2
- L. Oyen, “Nanoindentation hardness of mineralized tissues,” Journal of Biomechanics, Vol. 39, No. 14, 2006, pp. 2699-2702. doi:10.1016/j.jbiomech.2005.09.011
- P. K. Zysset, X. E. Guo, C. E. Hoffler, K. E. Moore and S. A. Goldstein, “Elastic modulus and hardness of cortical and trabecular bone lamellae measured by nanoindentation in the human femur,” Journal of Biomechanics, Vol. 32, No. 10, 1999, pp. 1005-1012. doi:10.1016/S0021-9290(99)00111-6
- J. Y. Rho, M. E. Roy II, T. Y. Tsui and G. M. Pharr, “Elastic properties of microstructural components of human bone tissue as measured by nanoindentation,” Journal of Biomedical Meterials Research, Vol. 45, No. 1, 1999, pp. 48-54.
- M. Todoh, S. Tadano and Y. Imari, “Effect of Heat Denaturation of Collagen Matrix on Bone Strength,” Proceedings of 13th International Conference on Biomedical Engineering, Singapore, Vol. 23, 3-6 December 2008, pp. 2034-2037.
- R. Akhtar, S. Morse and P. M. Mummery, “Nanoindentation of Bone in a Physiological Environment,” Materials Research Society Symposium Proceedings, Vol. 844, 2005, pp. 15-20.
- J. D. Currey, K. Brear, P. Zioupoa and G. C. Reilly, “Effect of Formaldehyde fixation on some mechanical properties of bovine bone,” Biomaterials, Vol. 16, No. 16, 1995, pp. 1267-1271. doi:10.1016/0142-9612(95)98135-2
- X. Wang, R. A. Bank, J. M. Teloppele, K. A. Athansiou and C. M. Agrawal, “Effect of Collagen Denaturation on Bone Biomechanical Integrity,” 45th Annual Meeting, Orthopaedic Research Society, Anaheim, 1-4 February 1999, p. 782.
- Z. Fan, J. G. Swadener, J. Y. Rho, M. E. Roy and G. M. Pharr, “Anisotropic properties of human tibial cortical bone as measured by nanoindentation,” Journal of Orthopaedic Research, Vol. 20, No. 4, 2000, pp. 806-810. doi:10.1016/S0736-0266(01)00186-3
- C. E. Hoffler, K. E. Moore, K. Kozloff, P. K. Zysset, M. B. Brown and S. A. Goldstein, “Heterogeneity of Bone Lamellar-Level Elastic Moduli,” Bone, Vol. 26, No. 6, 2000, pp. 603-609. doi:10.1016/S8756-3282(00)00268-4
- P. Roschger, E. P. Paschalis, P. Fratzl and K. Klaushofer, “Bone mineralization density distribution in health and disease,” Bone, Vol. 42, No. 3, 2008, pp. 456-466. doi:10.1016/j.bone.2007.10.021
- W. C. Oliver and G. M. Pharr, “An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments,” Journal of Biomedical Meterials Research, Vol. 7, No. 6, 1992, pp. 1564-1583. doi:10.1557/JMR.1992.1564
- D. Roylance, “Stress Strain Curve,” Department of Materials Science and Engineering, Massachusetts Institute of Technology, Cambridge, 1999. http://ocw.mit.edu/courses/materials-science-and-engineering/3-11-mechanics-of-materials-fall-1999/modules/ss.pdf
- R. D. Bloebaum, J. G. Skedros, E. G. Vajda, K. N. Bachus and B. R. Constantz, “Determining mineral content variations in bone using backscattered electron imaging,” Bone, Vol. 20, No. 5, 1997, pp. 485-490. doi:10.1016/S8756-3282(97)00015-X
- H. Trębacz and K. Wójtowicz, “Thermal stabilization of collagen molecules in bone tissue,” International Journal of Biological Macromolecules, Vol. 37, No. 5, 2005, pp. 257-262. doi:10.1016/j.ijbiomac.2005.04.007
- P. Zioupos, J. D. Currey and A. J. Hamer, “The role of collagen in the declining mechanical properties of aging human cortical bone,” Journal of Biomedical Meterials Research, Vol. 45, No. 2, 1999, pp. 108-116. doi:10.1002/(SICI)1097-4636(199905)45:2<108::AID-JBM5>3.0.CO;2-A
- X. Wang, R. A. Bank, J. M. TeKoppele and C. M. Agrawal, “The role of collagen in determining bone mechanical properties,” Journal of Orthopaedic Research, Vol. 19, No. 6, 2001, pp. 1021-1016. doi:10.1016/S0736-0266(01)00047-X
- J. Y. Rho, P. Zioupos, J. D. Currey and G. M. Pharr, “Microstructural elasticity and regional heterogeneity in human femoral bone of various ages examined by nanoindentation,” Journal of Biomechanics, Vol. 35, No. 2, 2002, pp. 189-198. doi:10.1016/S0021-9290(01)00199-3
- M. Raspanti, S. Guizzardi, V. De Pasquale, D. Martini and A. Ruggeri, “Ultrastructure of heat-Deproteinated compact hone,” Biomaterials, Vol. 15, No. 6, 1994, pp. 433- 437. doi:10.1016/0142-9612(94)90222-4
- J. L. Holden, J. G. Clement and P. P. Phakey, “Age and Temperature Related Changes to the Ultrastructure and Composition of Human Bone Mineral,” Journal of Bone and Mineral Research, Vol. 10, No. 9, 1995, pp. 1400-1409. doi:10.1002/jbmr.5650100918
NOTES
*Corresponding author.

