International Journal of Geosciences
Vol. 3 No. 3 (2012) , Article ID: 21196 , 9 pages DOI:10.4236/ijg.2012.33060
Prediction of Concrete Faced Rock Fill Dams Settlements Using Genetic Programming Algorithm
Civil Engineering Department, Shahid Bahonar University, Kerman, Iran
Email: marandi@uk.ac.ir, mahmoodvn@gmail.com
Received January 16, 2012; revised March 30, 2012; accepted April 7, 2012
Keywords: Concrete faced rock-fill dams; settlement; genetic programming algorithm; finite element model
ABSTRACT
In the present study a Genetic Programing model (GP) proposed for the prediction of relative crest settlement of concrete faced rock fill dams. To this end information of 30 large dams constructed in seven countries across the world is gathered with their reported settlements. The results showed that the GP model is able to estimate the dam settlement properly based on four properties, void ratio of dam’s body (e), height (H), vertical deformation modulus (Ev) and shape factor (Sc) of the dam. For verification of the model applicability, obtained results compared with other research methods such as Clements’ formula and the finite element model. The comparison showed that in all cases the GP model led to be more accurate than those of performed in literature. Also a proper compatibility between the GP model and the finite element model was perceived.
1. Introduction
One of the most important reasons of dam failures is uncontrolled settlements. Especially in the case of earth dams due to weak compaction and the use of improper materials this may occur. Such phenomenon may lead to very huge economic costs and human casualties but it has not been studied completely yet.
In the last centuries various concrete faced rock-fill dams are designed and constructed in many countries across the world. Exclusively in the past decades, the designing process and their construction has been changed considerably [1]. Such phenomenon occurred specially for the concrete faced rock fill dams. Recent growing demands for taller and larger dams, has changed the fundamental rules dominant in their design. This has led to new theories on the basis of new methods of testing materials and new techniques for the analysis.
Basically deformation of a dam may happen in three steps or situations: during the construction, during the first impounding, and while servicing. There are two basic approaches found in the literature for the estimation of the crest and body settlement in dams: 1) Numerical methods such as the finite element method, finite difference method; and 2) Experimental methods.
Almost all methods exist for prediction of dam deformations cover only one or two steps of the three steps mentioned above. For example, finite element method is used for the analysis of dam deformation during construction and first impounding. While, experimental methods are used for estimation of dam deformation during construction and servicing [2].
Sowers et al. in 1965 gathered information of 14 dams without attention to their heights, methods used in their section design, material used in the dam body and their construction methods and draw a scatter chart for height of dams over logarithm of the time. While better methods of construction e.g. better compaction or better proofing decrease the amount of settlement, they indicated that the settlement is independent of all these factors [3].
Lawton and Lester (1964) used data of 11 dams where, their settlement were at least 0.02 percent of their heights and presented in a settlement equation. The equation used depends only on the height and is not related to the time needed for the settlement [4].
Soydemir and Kjaemsli (1979) combined displacement equations in respect to time and height and obtained a new equation for the displacement of dam in various time periods using 48 different dam settlements data [5].
In 1984 Clements studied on 68 earth dams with well compacted poured concrete deck. He determined limits on the maximum and minimum of crest settlements and made a comparison between Soydemir and Kjaemsli method and real measured values in the field. The results showed that the method may have big errors (correlation about 0.247 to 0.897) in the estimation. Clements also suggested new deformation graphs for constructed dams which can be used in design and estimation of settlements [6].
Pinto and Marques Filho in 1998 presented a simple way for an approximate estimation of concrete faced rock-fill dams (CFRD) deformations. Their investigation showed that the void ratio and downstream valley shape have the most important effect on the deformation modulus1 of under construction dams. Accordingly for narrow valleys whose shape factors are less than 3.5, the effect of valley shape is higher than those with bigger shape factors2 (SF > 4). This means in wider hills the void ratio is more effective [8]. They also presented the following equation for the vertical deformation modulus.
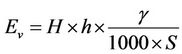 (1)
(1)
where Ev is vertical deformation modulus, H is embankment height above a determined point in meters, h is embankment height below a determined point, γ is embankment density in KN/m3 and s is the settlement of specified point in meter [9].
The Finite element method is a new method in comparison with the other methods used in the literature. Its reliability is highly dependent on the selected constitutive model for materials and an appropriate meshing which best cover the real environment. Kovacevic (1994), Duncan (1992, 1996) are the first investigators who used the finite element methods for the study of rock-fill embankment deformations during dam construction and the first impounding. They discussed on the analysis methods, limitations and combining different stress-strain models and their errors. Based on Duncan’s studies, a good correlation exists between the estimated and observed values [10-12].
Frequently, the estimation of dam properties is based on the experiments of previously constructed dams. There is much information published for estimation of concrete faced rock-fill dams. However these papers are written on the basis of limited information and in almost all cases concentrated on one or two of the effective parameters on rock modulus of elasticity or measured deformation. To overcome these limitations and present a simpler method, genetic programming algorithm which is of interest of various engineering fields can be aproposed method for the prediction of dam crests deformations. Due to high complexity and the presence of different variables in the soil responses, the genetic programming with a perfect training algorithm is extended. However, the authors could not find any data obtained for estimation of crest settlement of concrete faced rock-fill dams using GP algorithm in literature. In this paper an investigation is carried out on the deformation behavior of concrete faced rock-fill dams using GP modeling. For this purpose, documents from 30 information bases and from 7 countries across the world are used. The studies are concentrated on four effective parameters for prediction of dam crest settlement. These parameters are: void ratio of dam’s body (e), height of dam (H), vertical deformation modulus (Ev) and shape factor of the dam (SF). For training of the model, 67 percent of information (information of 21 dams out of 30 dams) is randomly selected and 33 percent of the rest (information of 9 dams) is used for dam prediction testing. To verify the suggested model with other methods in literature, the prediction results obtained for concrete faced rock-fill dams is compared with the Clement method.
2. Behavior Characteristics of Concrete Faced Rock-Fill Dams (CFRDs)
Due to the better performance and lower costs, construction of the concrete faced rock-fill dams (CFRDs) have been used wide spread since 4 decades ago. The CFRDs have become more common than rock-fill dams with clayey cores. Experience showed that even though these types of dams are economical and reliable, but in most cases the concrete decks are exposed to failure, damage and settlement. Table 1 shows performance and structural properties of CFRDs used in the present study [13].
Clements studied on the real settlements of 68 earth dams after construction and compared the results with the estimated values derived from the following equation:
 (2)
(2)
where S is the crest settlement in meters, H is the height of dam in meters, a and b are experimental constants of the equation. The constants values are given in Table 2.
Table 3 shows the measured values of the crest settlements of 35 dams in the fields and estimated values using Clements experimental equation for period of 10 years after construction. Statistical analysis between these two type of data shows that there is a weak correlation of R2 = 0.201 between the results. Therefore, it seems the Clements method is very conservative.
3. The Genetic Programing (GP) Model
3.1. Structure of the GP SDEL
In the recent years, the GP algorithm which is inspired by the nature and is based on the Darwin’ theory of evolution has been used for various purposes [7-14]. In 1992, John Koza used this algorithm as a specialization of the genetic algorithm (GA) with a difference that programs
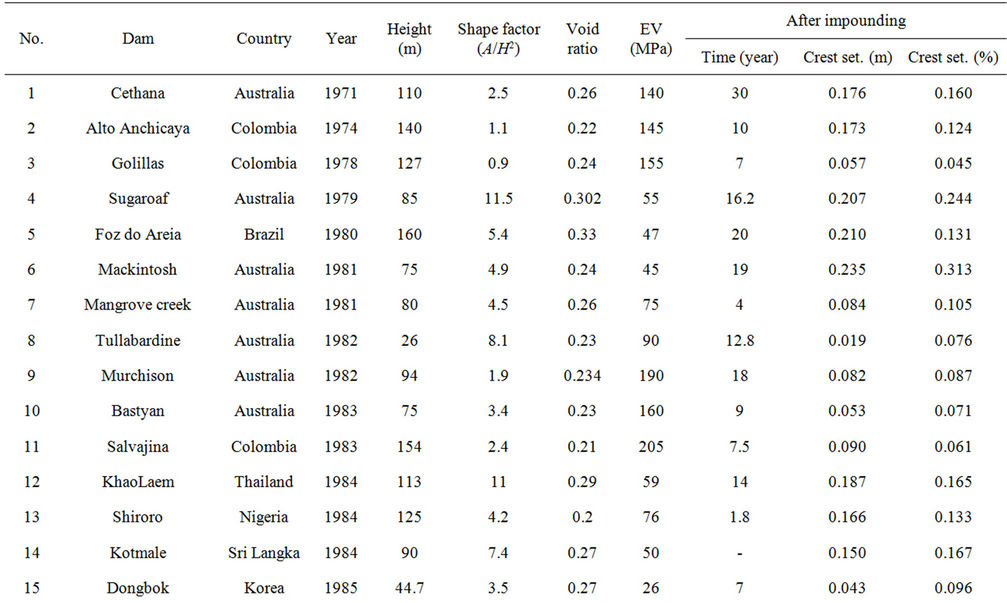
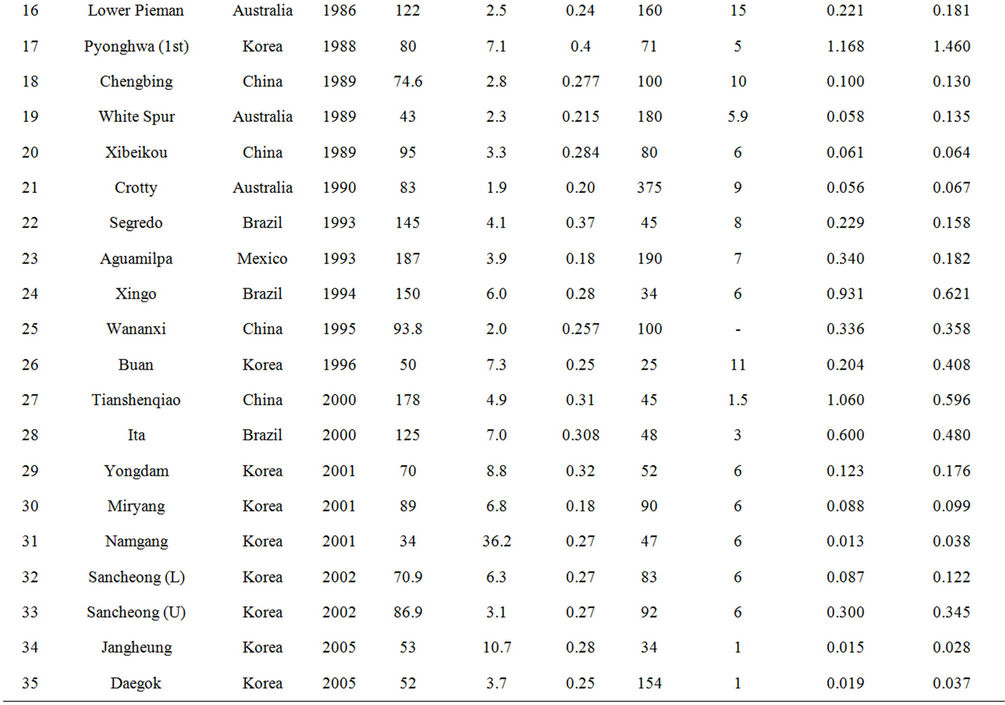
Table 1. Performance and structural properties of CRFDs [13].
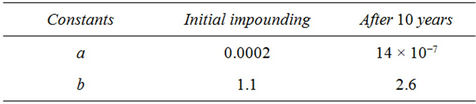
Table 2. Constants values of a and b [6].
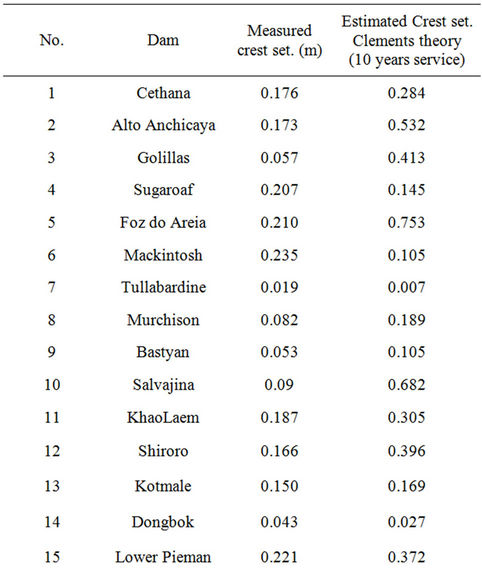
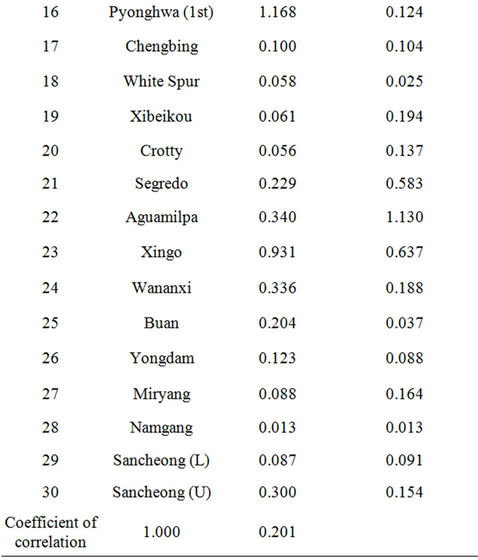
Table 3. Comparison of measured and estimated settlements values [13].
are replaced with individuals and establishes branches of a tree. Random changes are happened via replacement of the operators in the programs, changing value of a knot or replacement of the branches of the trees with each other [15,16]. Figure 1 shows three examples of GPs as trees.
The main characteristic of the GP algorithms is that they need a large population with thousands or even millions of individuals. Therefore, these algorithms are usually very slow and because of working on the basis of trees, more individuals in the population, more efficient and faster algorithms are obtained [14]. However, in general case, attaining a desired fitness value is very time consuming, but this is not very horrific because with one time of running the algorithm, a model attains which could be used simply for the problem. Another special characteristic of the GP is that, the answer is a model instead of a value which may be nonlinear. In addition to these aspects, in the standard form of GA, the lengths of chromosomes are constant, but in the GP algorithm these lengths might be variable. In the GP algorithm the first step is to make the first generation by creation of random programs. Each program has a fitness value that determines the chance of the program in the creation of the next generation. In the GP algorithms, two main operators which are necessary to make the next generations are crossover and mutation.
In the crossover process, a child program is made by changing the random parts of two selected parents. As shown in Figure 2, point C of the parent 1 and point D of the parent 2 are selected for the crossover process, and then the outcome children of such process are drawn. The mutation process in which, a child program is modified by altering a randomly selected part, is a guarantee for the existence of versatility in the population of a generation. An example of such process is shown in Figure 3 where, the mutation has been done in point C. A schematic flowchart for the creation of the generations in the GP algorithm is shown in Figure 4. At the present study, a GP model is proposed for the prediction of concrete faced rock fill dams settlements considering different variables that affect the results and the domain in which these variables changes. It is noteworthy that using the GP algorithms does not guarantee obtaining the most optimum result but it allows achieving an approvable result in a reasonable calculating time.
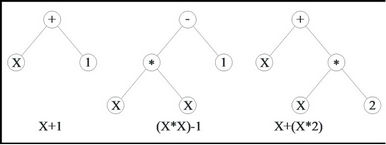
Figure 1. Examples of trees in the GP algorithm structure.
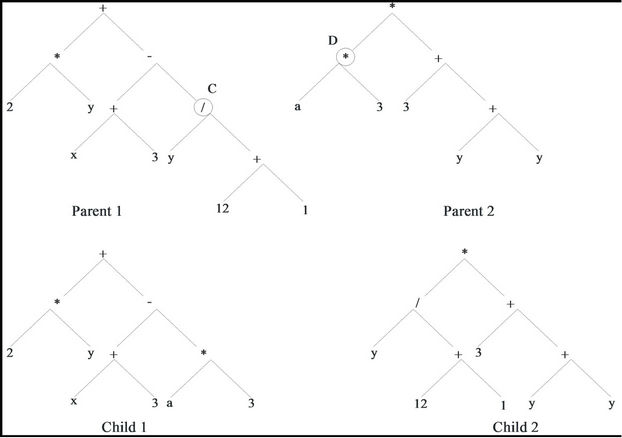
Figure 2. Example of crossover process.
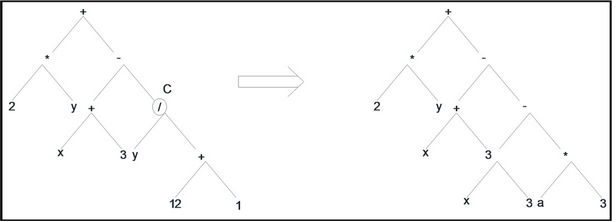
Figure 3. Example of mutation process.

Figure 4. A schematic flowchart for the creation of generations in the GP algorithm.
3.2. Initial Information for the GP Model
Paying attention to the information in Table 1, it can be seen that big differences exist between the times when settlements are measured. It is also perceived that the settlement would reach to a moderately persistent amount about 6 years after construction of the CFRs, so information of settlement before this age is not invokable. According to this, information of 5 dams includes Mangrove Greek, Tianshengiao, Ita, Janheung and Daegok has been ignored and information of 30 other dams has been used. The range of changes in the height and length of these dams are 26 - 187 m and 110 - 1168 m respectively. The input variables which are used for the prediction of the settlement are shape factor (SF), void ratio (e), height (H) and vertical deformation modulus (Ev) of dams. Table 4 shows the range at which these input parameters changes.
3.3. The GP Model for the Prediction of Dams Crest Settlements
A GP model is constructed on the basis of 67 percent of the all existing data (information of 21 dams of all 30 dams). The remaining information (the remaining nine dams) has been used for testing the model. The overall characteristics of the algorithm are presented in Table 5.
After training and using the above information, the model is finalized as follows:
Settlement = R* × R(3)
where R and R* are functions of the parametersas follows:
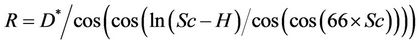
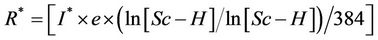
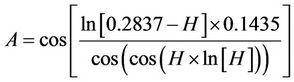
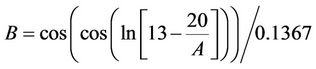

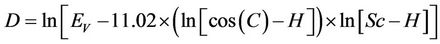
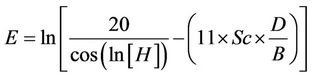
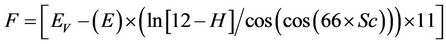
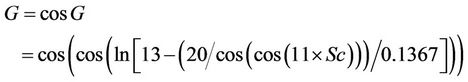
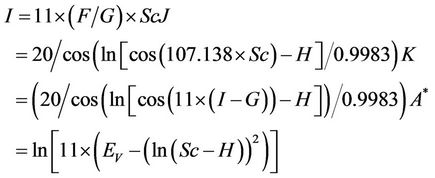
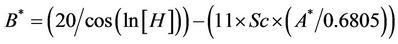
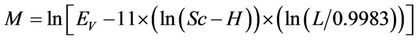
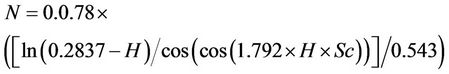
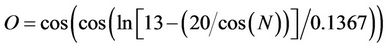
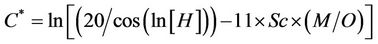


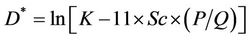
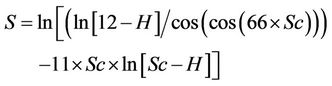
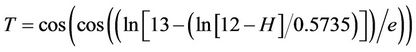

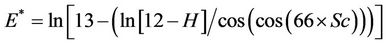
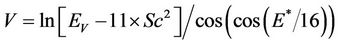
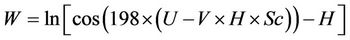
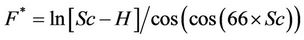
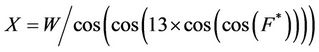

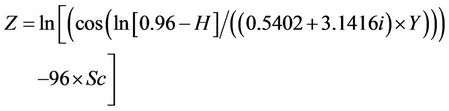
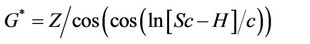
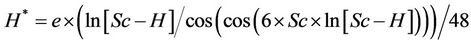
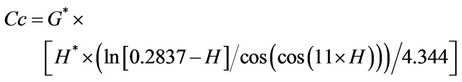
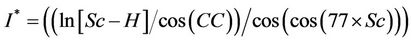
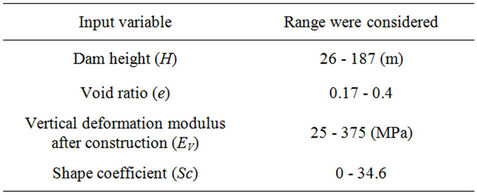
Table 4. Range of input parameters changes.
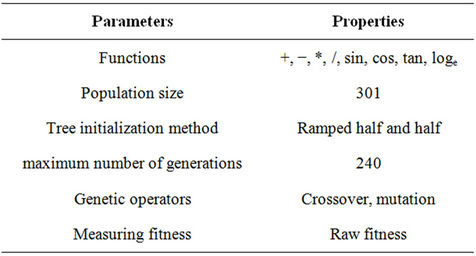
Table 5. The overall characteristics of the GP algorithm.
The number of knots in the model is 701 and its depth is 50. The results indicate that; there is a good agreement between the results and measured settlements with correlation factor of 0.98, and a proper performance for the model in the testing stage is achieved.
4. The Verification of the Trained Model
With training the model, and to demonstrate the efficiency of the algorithm for the prediction of the CFRDs settlements, information of 9 dams is used for the testing. To verify the trained model, the results obtained are compared with the findings of the Clements method. The reliability of the model and predicted values for the crest settlement obtained in the present work and the ones obtained by the Clements method is shown in Figure 5.
Table 6 shows the mean, standard deviation and the minimum least square error values between the measured values (using Clements model) and those obtained by present GP model. The results indicate that; even though the statistical analysis is derived from a limited set of information, however the performance of the present GP model is better in comparison with the Clements model. Due to the lack of physical model for testing and measurement of the crest settlement and for complex phenomena, it seems that; the presented GP algorithm has the capability for prediction of dam crest settlement.
5. Comparison between the GP and Finite Element Models
To evaluate and compare the results obtained by the GP and finite element models, the Daegok earth dam is modeled using the presented GP model and PLAXIS method. Daegok dam is a CFRD type dam with 52 m in height. The dam crest length and width are 190 m and 9.5 m respectively. The total volume of its body is 479 m3. The slope of the upstream face is 1V:1.4H, and for the downstream face is 1V:1.8H. The details of the dam section and construction procedures are shown in Figure 6 and Table 7 [9]. Tables 8 and 9 present the overall specifications of soils used in the dam model. Due to using rock material in the dam body, a hardening hyperbolic soil model is used for the analysis. It is assumed that the soil is homogenous in all cases. Table 8 describes the common properties of the Mohr-Coulomb and hardening models, while Table 9 contains complementary parameters belong only to the hardening model.
There are 14 computing phases in the Plaxis model. The first phase is considered for applying initial stresses. Due to slope existence, the gravity loading method is used. The other 13 phases are considered for modeling of the layered soils and three impounding steps of 15, 30 and 40 meters levels. Using this model, the long term settlement for the dam crest is 7.9 cm, while the dam settlement at the end period of construction is about 3 cm, which is shown in Figure 7. Using equation (1), for a point located near the dam crest, the vertical deformation modulus (Ev) is determined 138.8 MPa at the end of construction period as follow:
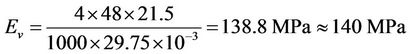 (4)
(4)
At this stage, using Equation (3) and the values of e = 0.25, H = 52 m, Sc = 3.7, and Ev = 140 MPa, the dam crest settlement is predicted by the GP model, which is equal to 7.8 cm. This finding is very close to the ones obtained by the finite element method. The results confirm the liability of the presented GP model.
6. Conclusions
In the present study which focused on the prediction of earth dam crest settlement using the genetic program
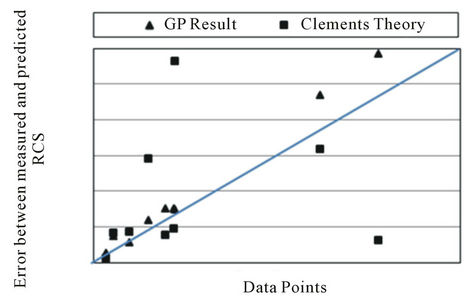
Figure 5. The results of present GP model in comparison with the Clements model.
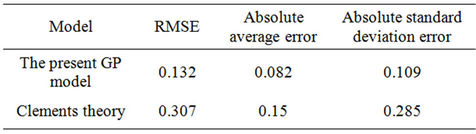
Table 6. Statistical comparison between the present GP model and Clements model.

Table 7. The construction time-table of Daegok Dam [9].

Figure 6. The Daegok dam cross section.
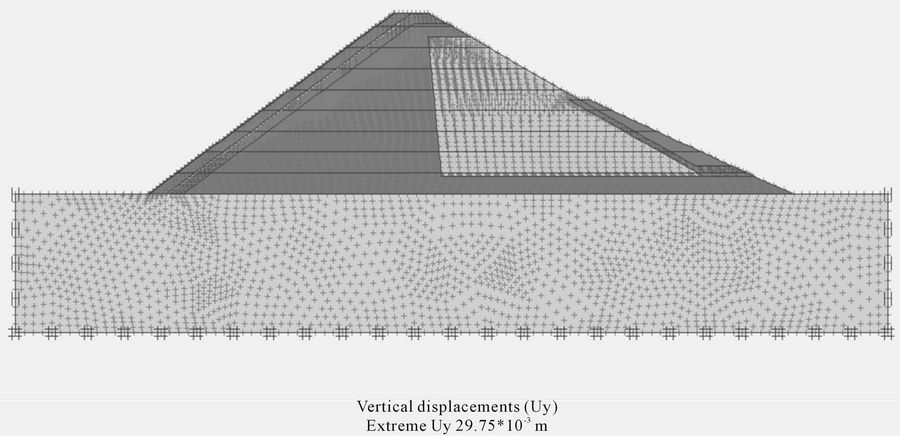
Figure 7. The crest settlement after dam construction.
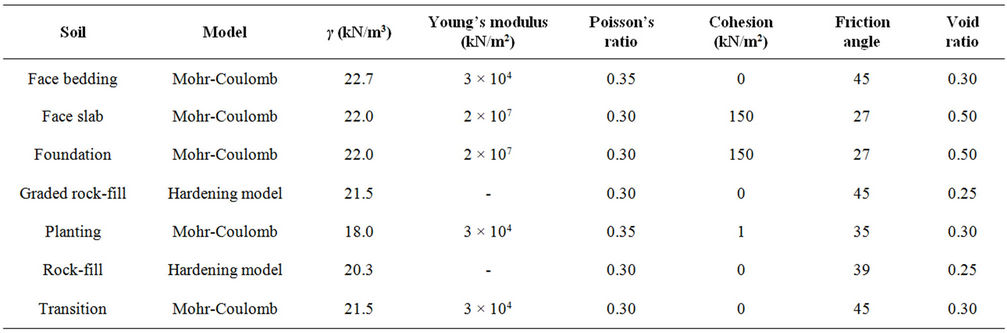
Table 8. Properties of soil in the hardening and Mohr-Coulomb models.
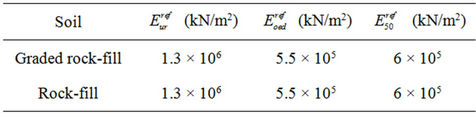
Table 9. Special properties for the soil hardening model.
ming model the following conclusions are made:
1) The results obtained by the GP model is in agree with the ones calculated through the experimental measurements.
2) The GP model, which is based on four characteristics of: Ev, H, e, and Sc has the best applicability and is in contrast with conventional methods such as Clements method, which only uses the H parameter for estimation of the crest settlement.
3) The results obtained by the GP model have a good compatibility with the finite element modeling.
4) The GP model is a trained model, and is capable of calculating the dam crest settlement without using any field laboratory tests.
5) The GP model can be used for complex problems, where rock-fill with various settlement aspects are involved.
6) Even though, the GP model is derived from a limited set of information and is not necessarily the most perfect one, however, the performance of this model is better in comparison with the conventional models such as: the Clements model.
7) The main weakness of the GP modeling is the time consuming and the needs for a huge population, but when the model is trained, many complex aspects can be predicted.
REFERENCES
- G. Hunter and R. Fell, “The Deformation Behavior of Rokfill,” Uniciv. Report No. 405, The University of New South Wales, Sydney, 2002.
- F. Saboya, R. Barosa and A. Vasconcelos, “The Influence of the Left Abutment Geometry on the Behaviour of Xingo Rock-Fill Dam,” Proceedings of the International Symposium on Concrete Faced Rock-Fill Dams, Beijing, 18 September 2000, pp. 565-572.
- G. F. Sowers, R. C. Williams and T. S. Wallace, “Compressibliity of Broken Rock and the Settlement of Rockfills,” Proceedings of the 6th International Conference on Soil Mechanics and Foundation Engineering, Toronto, Vol. 2, 1965, pp. 561-565.
- F. L. Lawton and M. D. Lester, “Settlement of Rockfill Dams,” Proceedings of the 8th International Congress on Large Dams, Edinburgh, Vol. 3, 1964, pp. 599-613.
- C. Soydemir and B. Kjaernsli, “Deformations of Membrane-Faced Rockfill Dams,” Proceedings of the 7th European Conference on Soil Mechanics and Foundation Engineering, Brighton, Vol. 3, 1979, pp. 281-284.
- R. P. Clements, “Post-Construction Deformation of Rockfill Dams,” Journal of Geotechnical Engineering, Vol. 110, No. 7, 1984, pp. 821-840. doi:10.1061/(ASCE)0733-9410(1984)110:7(821)
- M. D. Fitzpatrick, B. A. Cole, F. L. Kinstler and B. P. Knoop, “Design of Concrete-Faced Rockfill Dams,” In: J. B. Cooke and J. L. Shererd, Eds., Concrete Face Rockfill Dams-Design, Construction, and Performance, 1985, pp. 410-434.
- N. L. S. Pinto and P. L. M. Filho, “Estimating the Maximum Face Slab Deflection in CFRDs,” Hydropower & Dams, Vol. 5, No. 6, 1998, pp. 28-30.
- P. Han-Gyu, S. Min-Woo, K. Yong-Soeng and L. HeiuDae, “Settlement Behavior Characteristics of CFRD in Construction Period-Case of Daegok Dam,” Journal of the KGS, Vol. 21, No. 7, 2005, pp. 91-105.
- N. Kovacevic, “Numerical Analyses of Rockfill Dams, Cut Slopes and Road Embankments,” Ph.D. Thesis, Imperial College of Science, Technology and Medicine, London, 1994.
- J. M. Duncan, “State of the Art: Static Stability and Deformation Analysis,” ASCE Geotechnical Special Publication, Vol. 1, No. 31, 1992, pp. 222-266.
- J. M. Duncan, “State of the Art: Limit Equilibrium and Finite-Element Analysis of Slopes,” ASC.E Journal of Geotechnical Engineering, Vol. 122, No. 7, 1996, pp. 577-595. doi:10.1061/(ASCE)0733-9410(1996)122:7(577)
- Y. S. Kim and B. T. Kim, “Prediction of Relative Crest Settlement of Concrete-Faced Rockfill Dams Analyzed Using an Artificial Neural Network Model,” Computers and Geotechnics, Vol. 35, No. 1, 2008, pp. 313-322. doi:10.1016/j.compgeo.2007.09.006
- Y. Zhang and S. Bhattacharyya, “Genetic Programming in Classifying Large-Scale Data: An Ensemble Method,” Information Sciences, Vol. 163, No. 1-3, 2004, pp. 85- 101. doi:10.1016/j.ins.2003.03.028
- J. R. Koza, “Genetic Programming: On the Programming of Computers by Means of Natural Selection,” 6th Printing, Massachusetts Institute of Technology, Cambridge, 1998.
- J. R. Koza, M. A. Keane, M. J. Streeter, J. Matthew, W. Mydlowec, J. Yu and G. Lanza, “Genetic Programming IV: Routine Human-Competitive Machine Intelligence,” Springer, New York, 2005.
NOTES
1For determining deformation behavior of rocks, deformation modulus during construction (Erc) and during the first filling (Erf) are defined which are related to its void ratio and the bed rock properties. Theoretically vertical deformation modulus (Ev) gradually decreases with increase in the dam’s height [7].
2SF = A/H2 where H is embankment height in meters and A is the area of upstream deck area in squared meters.

