Open Journal of Fluid Dynamics
Vol.3 No.2(2013), Article ID:33671,6 pages DOI:10.4236/ojfd.2013.32017
On the Boundary Layer Flow over a Moving Surface in a Fluid with Temperature-Dependent Viscosity
1Department of Mathematics, University of Dar es Salaam, Dar es Salaam, Tanzania
2Cape Peninsula University of Technology, Bellville, South Africa
Email: ewambui02@gmail.com
Copyright © 2013 E. W. Mureithi et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 25, 2013; revised April 28, 2013; accepted May 6, 2013
Keywords: Flat Moving Surface; Temperature Dependent Viscosity; Self-Similar Equations; Viscous Dissipation
ABSTRACT
This paper examines a boundary layer flow over a continuously moving heated flat surface with velocity 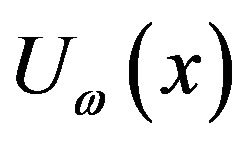 in a streaming flow with velocity
in a streaming flow with velocity 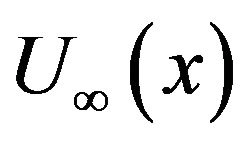 and with temperature dependent viscosity,
and with temperature dependent viscosity,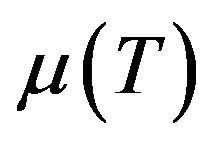 . The momentum and the energy equations are coupled through the viscous dissipation term. The coupled boundary layer equations are transformed into a self-similar form using an appropriate similarity variable. An efficient numerical technique is used to solve the self-similar boundary layer equations. It is shown that at low enough values for the velocity ratio
. The momentum and the energy equations are coupled through the viscous dissipation term. The coupled boundary layer equations are transformed into a self-similar form using an appropriate similarity variable. An efficient numerical technique is used to solve the self-similar boundary layer equations. It is shown that at low enough values for the velocity ratio , an increase in viscous dissipation enhances greatly the local heat transfer leading to temperature overshoots adjacent to the wall. The viscosity variation parameter is shown to have significant effects on the temperature dependent viscosity and the velocity and temperature distribution within the boundary layer.
, an increase in viscous dissipation enhances greatly the local heat transfer leading to temperature overshoots adjacent to the wall. The viscosity variation parameter is shown to have significant effects on the temperature dependent viscosity and the velocity and temperature distribution within the boundary layer.
1. Introduction
Studies on heat and mass transfer in boundary layers over continuously moving or stretching surfaces have been increasing due to their wide variety of applications in manufacturing processes such as glass-fibre production, metal extrusion, materials-handling conveyors and paper production.
One of the earliest studies on boundary-layer flow past moving surfaces was initiated by Sakiadis [1], who investigated momentum transfer for a flow over a continuously moving plate in quiescent fluid. The results of Sakiadis were later verified experimentally by Tsou et al. [2]. Over recent years studies of boundary layer past moving or stretching surfaces in otherwise quiescent fluids included the work of Ali [3] who investigated similarity solutions for a thermal boundary layer over a power-law stretching surface with suction or injection; Elbashbeshy [4] who studied heat transfer over a stretching surface with suction or injection; Magyari and Keller [5] who studied similarity solutions for boundary layer flow over an exponentially stretching surface and Mureithi [6] who examined linear stability properties of a boundary layer flow over a moving surface in a streaming flow.
Studies on free-stream effects on boundary-layer flows over moving or stretching surfaces included the work of Abdelhafez [7] and Chappidi and Gunnerson [8] who independently considered flows over moving surfaces in which both the surface and the free stream moved in the same direction. In their studies, they formulated two sets of boundary value problems for the cases 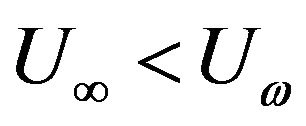 and
and . Afzal [9] formulated a single set of equations using as reference velocity a composite velocity given by
. Afzal [9] formulated a single set of equations using as reference velocity a composite velocity given by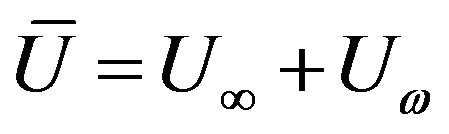 . Later Lin and Huang [10] used Afzal’s formulation to study momentum and heat transfer for a flow over a surface moving parallel or reversely to the free stream with temperature dependent viscosity. A study by Afzal [11] investigated momentum transfer on a power law stretching surface with free-stream pressure gradient.
. Later Lin and Huang [10] used Afzal’s formulation to study momentum and heat transfer for a flow over a surface moving parallel or reversely to the free stream with temperature dependent viscosity. A study by Afzal [11] investigated momentum transfer on a power law stretching surface with free-stream pressure gradient.
The current study investigates a boundary layer flow over a moving surface in a streaming flow with a temperature dependent dynamic viscosity,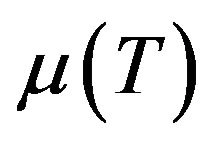 . The Ling and Dybbs [12] model for
. The Ling and Dybbs [12] model for  is used in this study.
is used in this study.
In Section 2, we formulate the problem. In Section 3, boundary layer equations are reduced to the self-similar form. In Section 4, numerical solutions for the self-similar boundary layer equations are presented and discussed and conclusions are drawn in Section 5.
2. Problem Formulation
An incompressible flow past an infinite surface continuously moving with velocity  in a streaming flow with velocity
in a streaming flow with velocity 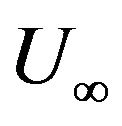 and with temperature dependent viscosity
and with temperature dependent viscosity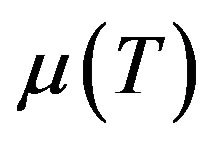 , is investigated. The fluid is of density
, is investigated. The fluid is of density , thermal conductivity
, thermal conductivity  and specific heat capacity
and specific heat capacity 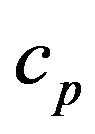 (at constant pressure). The boundary layer equations are
(at constant pressure). The boundary layer equations are
 (1)
(1)
The boundary conditions for this flow are
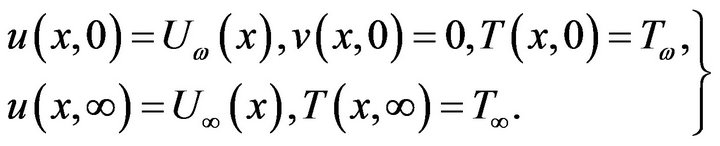 (2)
(2)
for a flow over an impermeable surface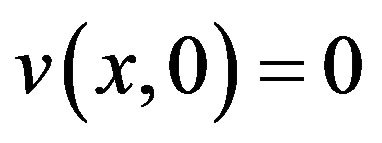 .
.
The following temperature dependent viscosity model due to Ling and Dybbs [12] is used here:
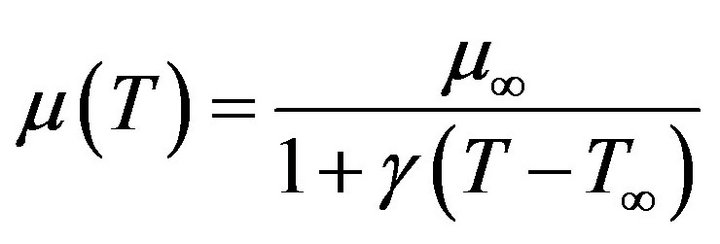
where 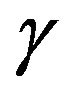 is a constant,
is a constant, 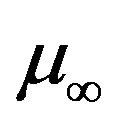 is the constant reference viscosity in the absence of heating. The case
is the constant reference viscosity in the absence of heating. The case 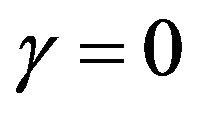 corresponds to the constant viscosity situation.
corresponds to the constant viscosity situation.
3. Self-Similar Boundary Layer Equations
The basic flow is rendered in non-dimensional form through setting

where 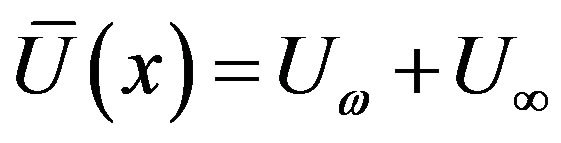 is the reference velocity (Afzal et al. [9]),
is the reference velocity (Afzal et al. [9]), 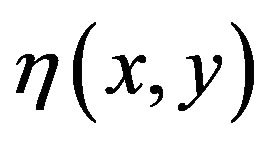 is the boundary-layer similarity variable and
is the boundary-layer similarity variable and  and
and  are the scaled free-stream velocity and temperature, respectively. The parameter
are the scaled free-stream velocity and temperature, respectively. The parameter 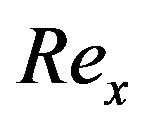 is the local Reynolds number defined as
is the local Reynolds number defined as
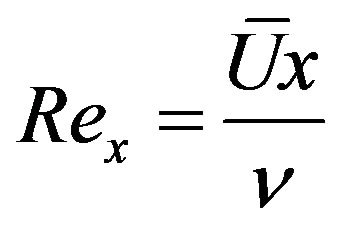 .
.
In non-dimensional form, the Lings-Dybbs model becomes
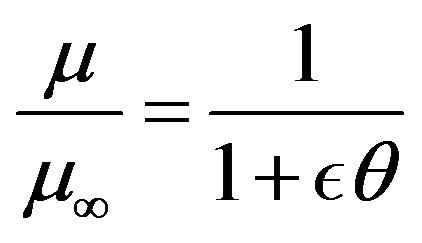
where 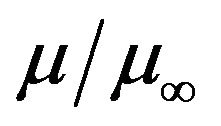 is the dimensionless dynamic viscosity and
is the dimensionless dynamic viscosity and 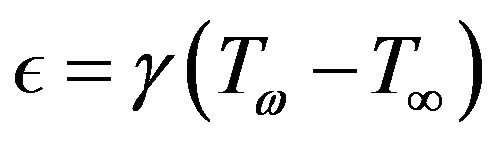 is the variable viscosity parameter. The case
is the variable viscosity parameter. The case 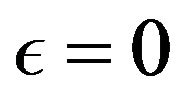 is equivalent to the case
is equivalent to the case  corresponding to constant viscosity.
corresponding to constant viscosity.
From the equation of continuity we have
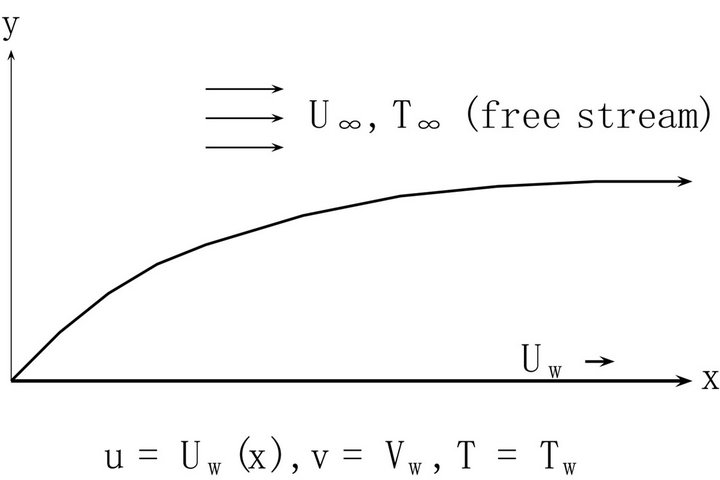
Figure 1. Schematic diagram for the problem.
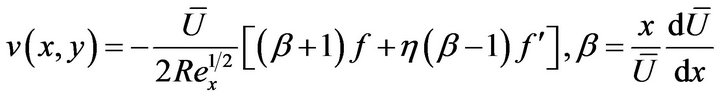
where the parameter  reduces to the pressure gradient parameter
reduces to the pressure gradient parameter
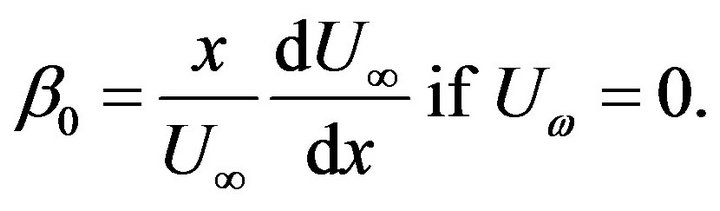
We assume power-law variations in the free-stream velocity and wall velocity of the form 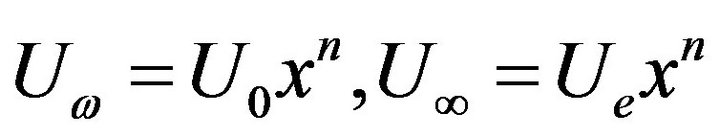 so that.
so that.
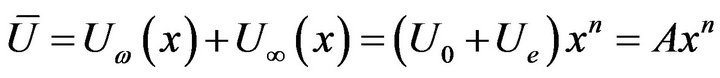
and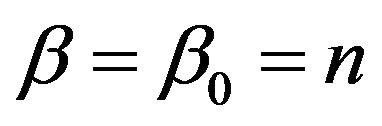 . The dimensionless similarity boundarylayer equations take the form
. The dimensionless similarity boundarylayer equations take the form
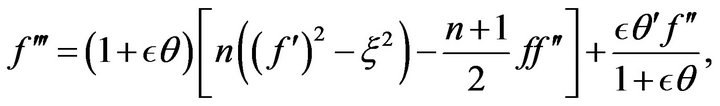 (3)
(3)
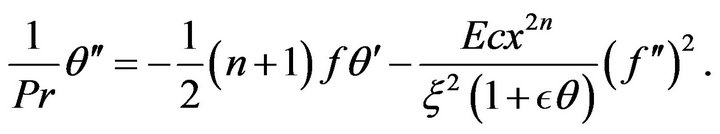 (4)
(4)
with boundary conditions
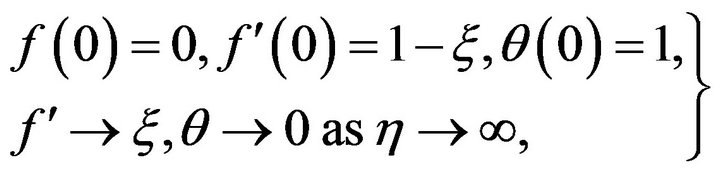 (5)
(5)
where
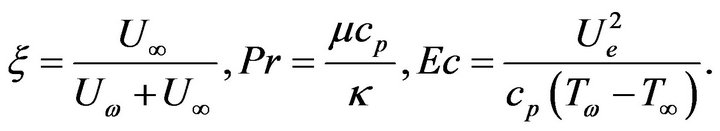
The parameter 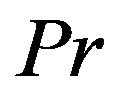 is the Prandtl number and
is the Prandtl number and 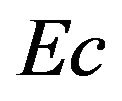 is the Eckert number. The flow is self-similar if one of the following is satisfied:
is the Eckert number. The flow is self-similar if one of the following is satisfied:
1. n = 0 for any Ec.
2. Ec = 0 for any n (negligible viscous dissipation).
remarks We have assumed that both the wall and the free stream move in the same direction so that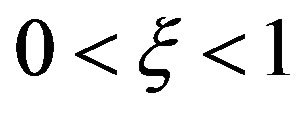 . The case when
. The case when  is corresponds to a wall moving in an otherwise quiescent fluid
is corresponds to a wall moving in an otherwise quiescent fluid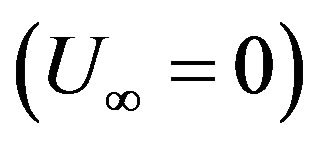 ,
, 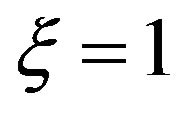 corresponds to flow over a stationary wall
corresponds to flow over a stationary wall 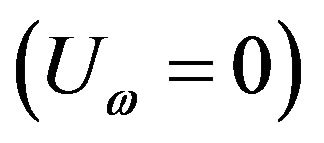 and
and 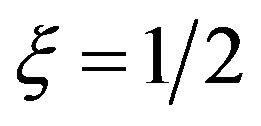 is equivalent to
is equivalent to 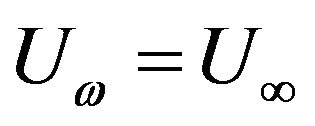 so that the wall and the freestream move with the same speed. When
so that the wall and the freestream move with the same speed. When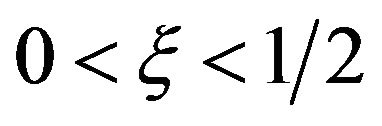 , the wall moves faster that the free-stream while the case when
, the wall moves faster that the free-stream while the case when 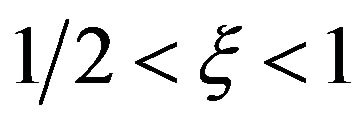 corresponds to the free-stream moving faster than the wall.
corresponds to the free-stream moving faster than the wall.
The surface shear stress and surface heat transfer are represented using the local skin friction factor,  , and the local Nusselt number,
, and the local Nusselt number,  , respectively defined as
, respectively defined as
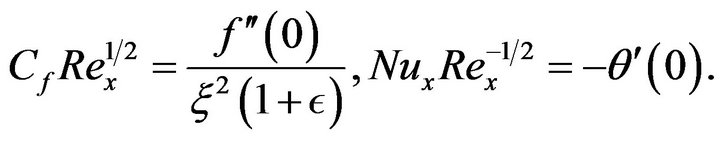
4. Numerical Solution and Discussion of Results
The coupled self-similar boundary layer Equations (3) and (4) together with the boundary conditions (5) are solved numerically using a shooting method coupled with the fourth-order Runge-Kutta scheme.
The results presented here are for the cases when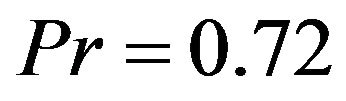 . Self-similar solutions were obtained for two cases. Case one is the flow viscous dissipation and
. Self-similar solutions were obtained for two cases. Case one is the flow viscous dissipation and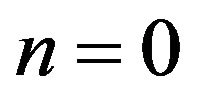 . Case two corresponds to the case with
. Case two corresponds to the case with 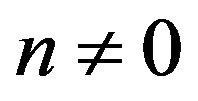 but without viscous dissipation effects.
but without viscous dissipation effects.
Figures 2 and 3 show that the effect of varying the fluid viscosity variation parameter 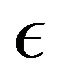 on the temperaturedependent dynamic viscosity,
on the temperaturedependent dynamic viscosity, 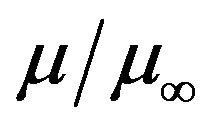 and the streamwise velocity
and the streamwise velocity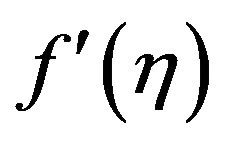 , within the boundary layer. At any location within the boundary layer
, within the boundary layer. At any location within the boundary layer 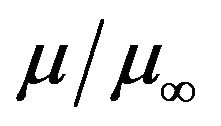 decreases with increase in the viscosity parameter,
decreases with increase in the viscosity parameter,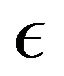 . The boundary layer thickness is found to decrease with increase in
. The boundary layer thickness is found to decrease with increase in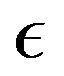 . The parameter
. The parameter 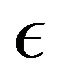 is a measure of fluid viscosity variation.
is a measure of fluid viscosity variation.
The effect of varying viscous dissipation parameter, 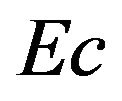 , and the velocity ratio
, and the velocity ratio  on the temperature distribution in the boundary layer is shown in Figures 4 and 5. Figure 4 shows that for
on the temperature distribution in the boundary layer is shown in Figures 4 and 5. Figure 4 shows that for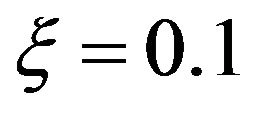 , increasing
, increasing 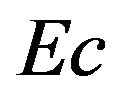 results in temperature over-shoot near the wall, with peaks in creasing with increase in
results in temperature over-shoot near the wall, with peaks in creasing with increase in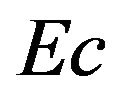 . Figure 5 illustrates the effect of varying the velocity ratio on the temperature distribution. For the case when
. Figure 5 illustrates the effect of varying the velocity ratio on the temperature distribution. For the case when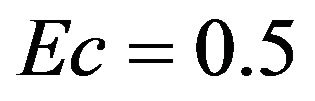 , the results show that the temperature peaks are realized for
, the results show that the temperature peaks are realized for 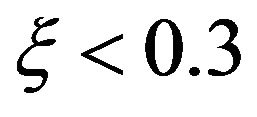 and the peaks amplitudes increase with decrease in
and the peaks amplitudes increase with decrease in .
.
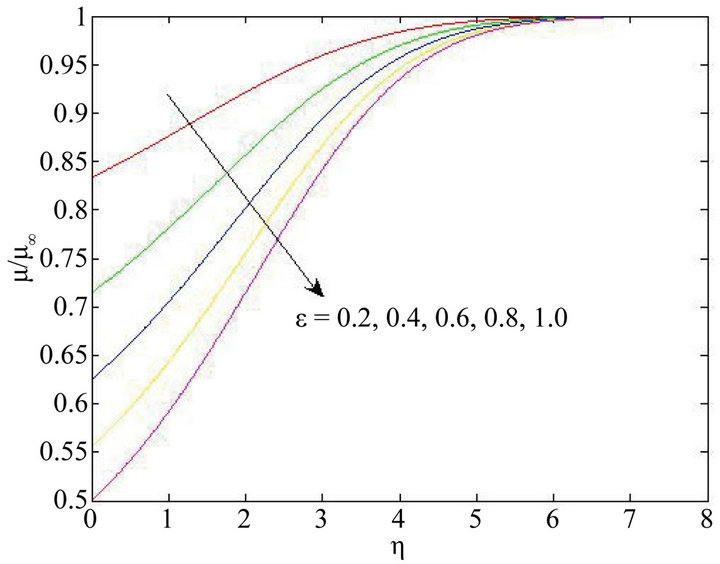
Figure 2. Effects of viscosity variation parameter on the dynamic viscosity for 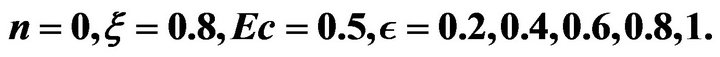
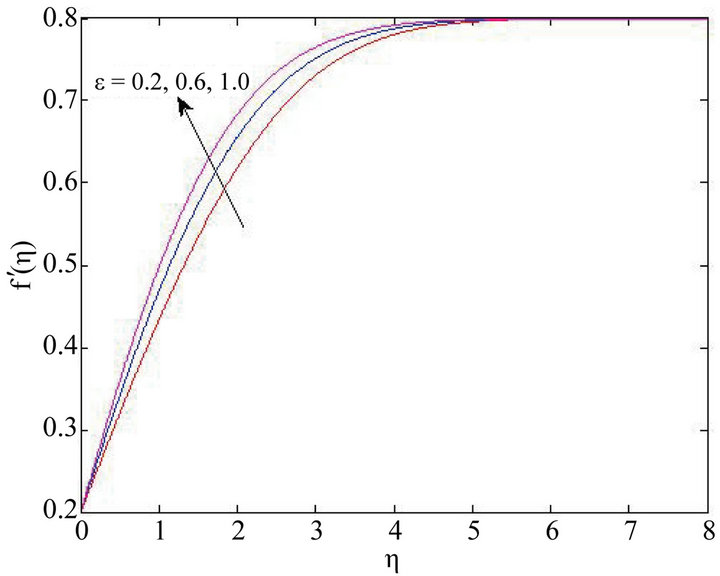
Figure 3. Effects of viscosity variation parameter on velocity profiles for  .
.
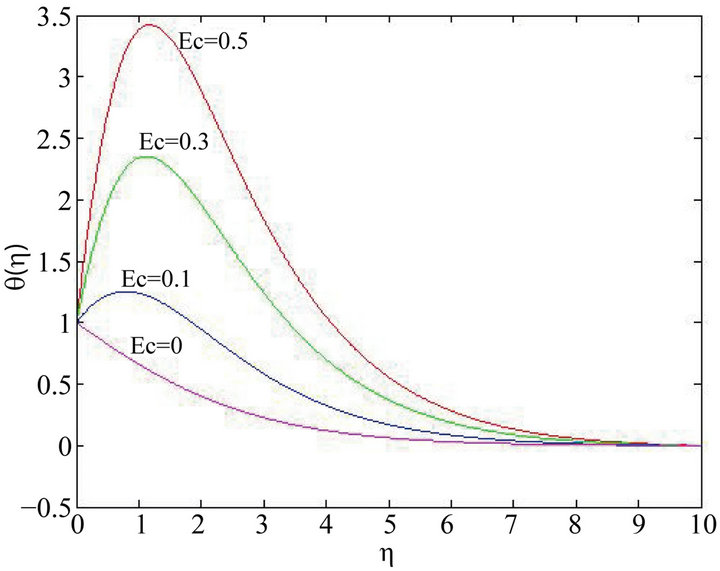
Figure 4. Effects of varying 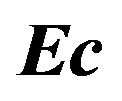 on temperature distribution for
on temperature distribution for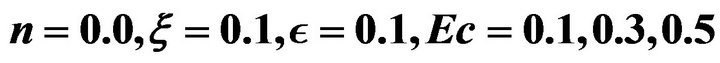 .
.
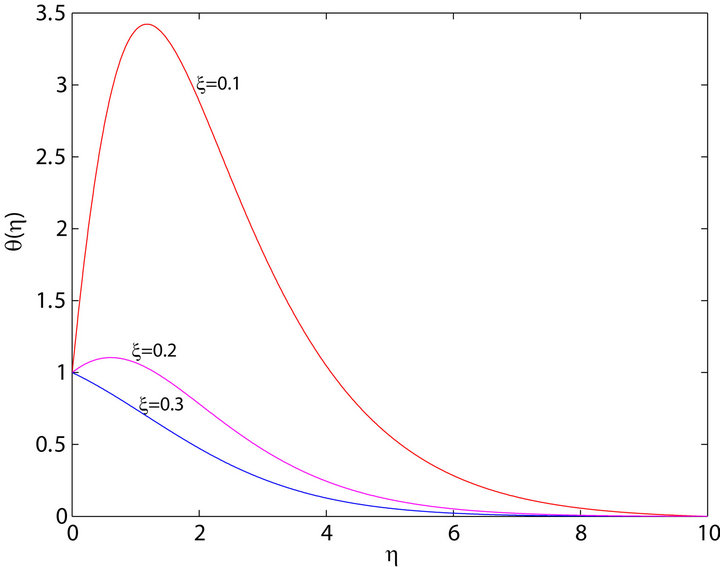
Figure 5. Effects of viscosity variation on the temperature distribution profiles for  .
.
The skin-friction is presented as a function of 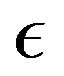 in Figures 6 and 7. These figures show the effect of varying
in Figures 6 and 7. These figures show the effect of varying  on the local skin friction coefficient for the case when
on the local skin friction coefficient for the case when 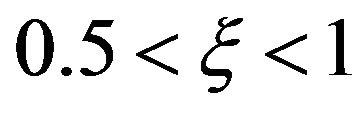 and
and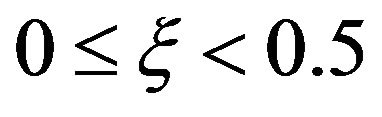 . For the case when
. For the case when 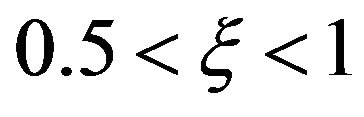 , the local skin friction coefficient is positive and hence the fluid exerts a dragging force on the wall. For this case, increasing
, the local skin friction coefficient is positive and hence the fluid exerts a dragging force on the wall. For this case, increasing  results in increase in the skin friction coefficient. For the case when
results in increase in the skin friction coefficient. For the case when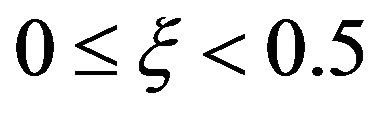 , the local skin friction coefficient is negative, which is an indication that the wall drags the fluid. Also, increasing
, the local skin friction coefficient is negative, which is an indication that the wall drags the fluid. Also, increasing 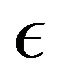 results in a decrease in the skin friction.
results in a decrease in the skin friction.
In Figure 8, the effect of varying  on local Nusselt number is shown as a function of
on local Nusselt number is shown as a function of 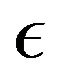 for the cases when
for the cases when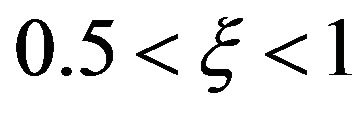 . The results show that the heat transfer coefficient decreases with increase in
. The results show that the heat transfer coefficient decreases with increase in  and increases with increase in
and increases with increase in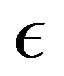 .
.
The results shown in Figure 9 are interesting. It is shown that for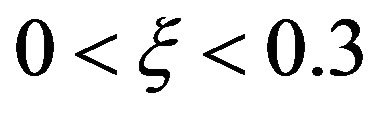 , the local Nusselt number is
, the local Nusselt number is

Figure 6. The skin friction coefficient against  for the case when
for the case when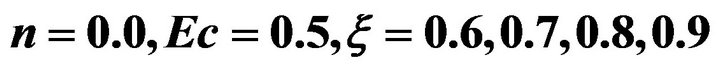 .
.

Figure 7. The skin friction coefficient against  for the case when
for the case when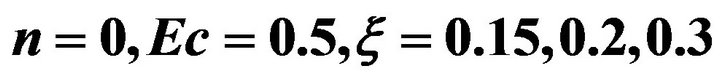 .
.
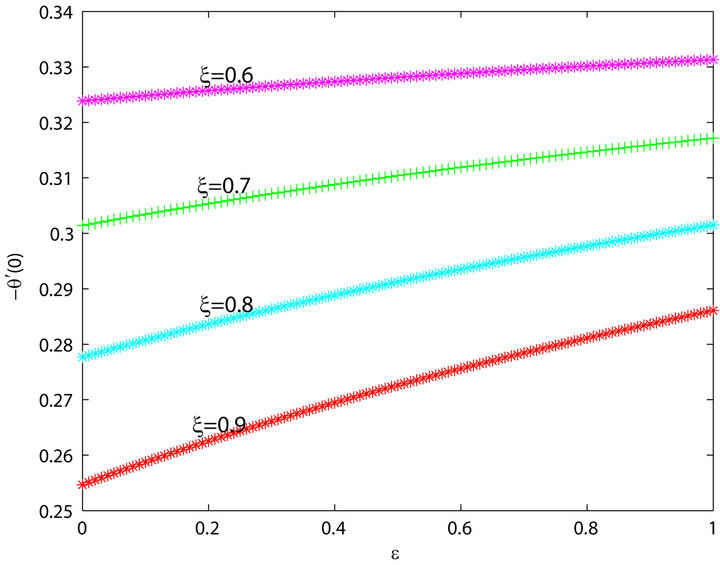
Figure 8. The heat transfer coefficient against 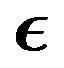 for the case when
for the case when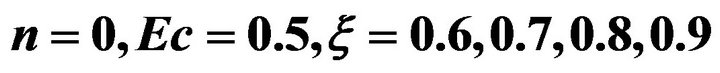 .
.
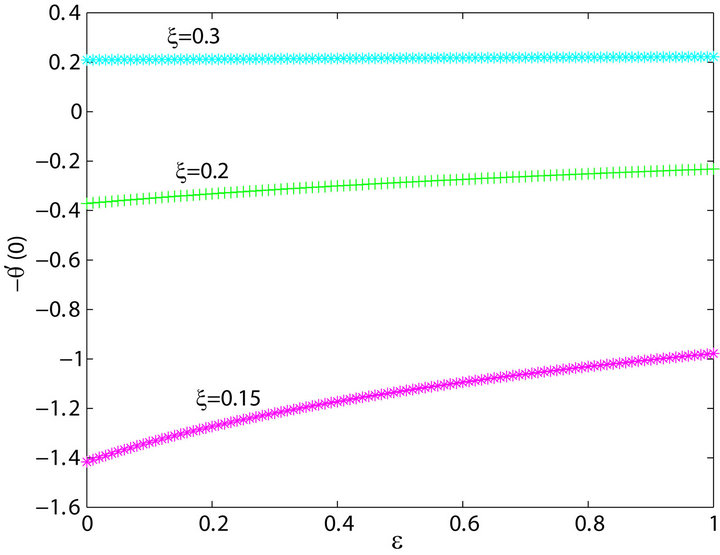
Figure 9. The heat transfer coefficient against  for the case when
for the case when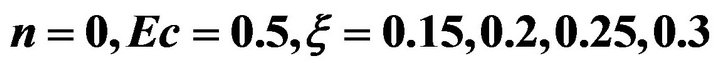 .
.
negative, changing sign to positive for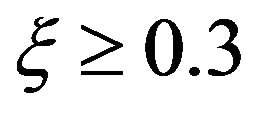 . This explains the results observed in Figure 7 where temperature over-shoot were observed adjacent to the wall. These results show that for low enough values for
. This explains the results observed in Figure 7 where temperature over-shoot were observed adjacent to the wall. These results show that for low enough values for , the heat transfer from wall to the fluid is greatly enhanced resulting in temperature over-shoots adjacent to the wall.
, the heat transfer from wall to the fluid is greatly enhanced resulting in temperature over-shoots adjacent to the wall.
The effect of varying 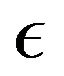 on the velocity and temperature distribution within the boundary layer is presented in Figures 10 and 11 for the case when wall is moving faster than the free-stream. The results show that velocity boundary layer thickness decreases with increase
on the velocity and temperature distribution within the boundary layer is presented in Figures 10 and 11 for the case when wall is moving faster than the free-stream. The results show that velocity boundary layer thickness decreases with increase  and that the temperature peaks decrease with increase in
and that the temperature peaks decrease with increase in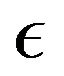 . This shows that the increasing
. This shows that the increasing  results in a decrease in heat transfer from the wall to the fluid.
results in a decrease in heat transfer from the wall to the fluid.
5. Conclusions
A self-similar boundary layer flow has been presented
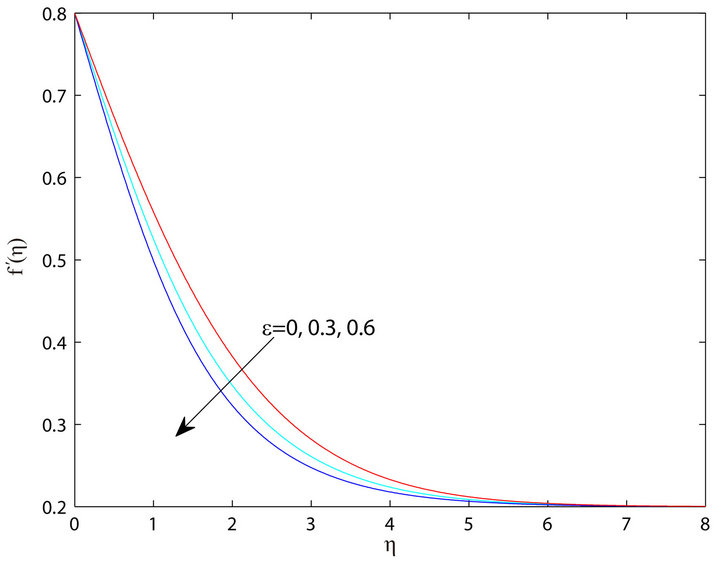
Figure 10. Effects of varying 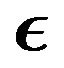 on the velocity distribution
on the velocity distribution 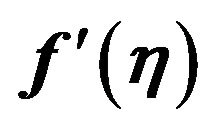 for
for 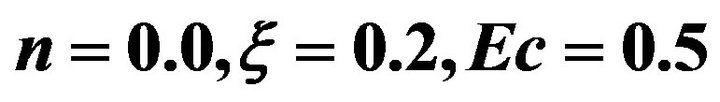 and
and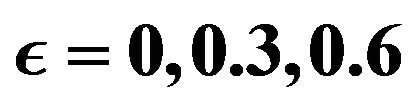 .
.
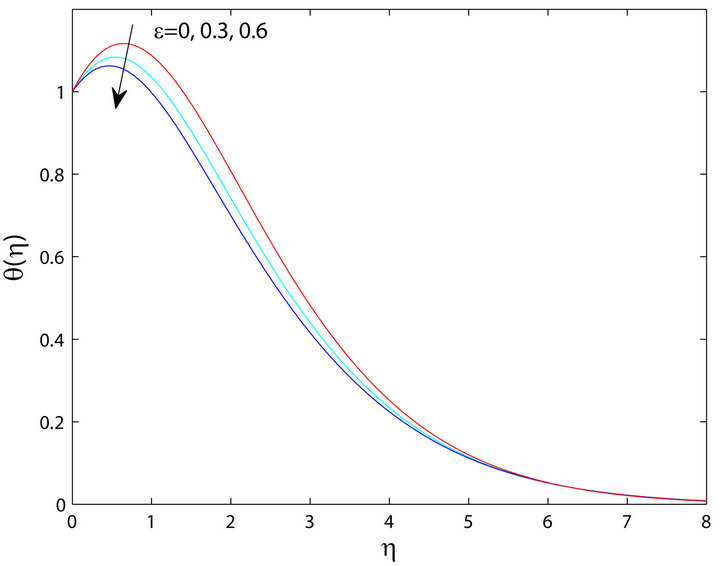
Figure 11. Effects of varying 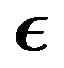 on the temperature distribution
on the temperature distribution 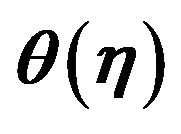 for n = 0.0, ξ = 0.2, Ec = 0.5 and
for n = 0.0, ξ = 0.2, Ec = 0.5 and  = 0, 0.3, 0.6.
= 0, 0.3, 0.6.
for a flow over a continuously moving heated surface in a fluid with temperature dependent viscosity. The selfsimilar equations were solved numerically and the results are presented in graphs.
In this study the effects of varying the viscosity variation 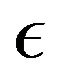 and the velocity ratio
and the velocity ratio  are investigated for the case when the surface moves in the same direction as the free-stream.
are investigated for the case when the surface moves in the same direction as the free-stream.
For low enough values for the velocity ratio ξ, the local heat transfer is found to be negative, indicating the heat transfer from the wall to the fluid is greatly enhanced near the wall as the Eckert number increases. This is seen in the temperature distribution profiles where temperature peaks are observed adjacent to the wall.
For the case when the wall moves faster than the fluid, the skin friction coefficient is negative, indicating that wall drags the fluid. The reverse occurs for the case when  where the skin friction is positive and hence the free-stream exerts a dragging force on the boundary layer.
where the skin friction is positive and hence the free-stream exerts a dragging force on the boundary layer.
REFERENCES
- B. C. Sakiadis, “Boundary Layer Behavior on Continuous Solid Surfaces: II Boundary Layer on a Continuous Flat Surface,” American Institute of Chemical Engineers Journal, Vol. 7, No. 2, 1961, pp. 221-225. doi:10.1002/aic.690070211
- F. Tsou, E. M. Sparrow and J. R. Goldstein, “Flow and Heat Transfer in the Boundary Layer on a Continuous Moving Surface,” International Journal of Heat and Mass Transfer, Vol. 10, No. 2, 1967, pp. 219-235. doi:10.1016/0017-9310(67)90100-7
- M. E. Ali, “On the Thermal Boundary Layer on a PowerLaw Stretched Surface with Suction or Injection,” International Journal of Heat and Fluid Flow, Vol. 16, No. 4, 1995, pp. 280-290. doi:10.1016/0142-727X(95)00001-7
- E. M. Elbashbeshy, “Heat Transfer over a Stretching Surface with Variable Surface Heat Flux,” Journal of Physics D: Applied Physics, Vol. 31, No. 16, 1998, pp. 1951- 1954. doi:10.1088/0022-3727/31/16/002
- E. Magyari and B. Keller, “Heat and Mass Transfer in the Boundary Layer on an Exponentially Stretching Continuous Surface,” Journal of Physics D: Applied Physics, Vol. 32, No. 5, 1999, pp. 577-585. doi:10.1088/0022-3727/32/5/012
- E. W. Mureithi, “Stability Properties of a Boundary Layer Flow Past a Continuously Moving Wall in a Streaming Flow,” International Journal of Fluid Mechanics Research, Vol. 33, No. 5, 2006, pp. 430-444. doi:10.1615/InterJFluidMechRes.v33.i5.40
- T. A. Abdelhafez, “Skin Friction and Heat Transfer on a Continuous Flat Surface Moving in a Parallel Free Stream,” International Journal of Heat and Mass Transfer, Vol. 28, No. 6, 1985, pp. 1234-1237. doi:10.1016/0017-9310(85)90132-2
- P. R. Chappidi and F. S. Gunnerson, “Analysis of Heat and Momentum Transport along a Moving Surface,” International Journal of Heat and Mass Transfer, Vol. 32, No. 7, 1989, pp. 1383-1386. doi:10.1016/0017-9310(89)90039-2
- N. Afzal, A. Badaruddin and A. A. Elgarvi, “Momentum and Heat Transport on a Continuous Flat Surface Moving in a Parallel Stream,” International Journal of Heat and Mass Transfer, Vol. 36, No. 13, 1993, pp. 3399-3403. doi:10.1016/0017-9310(93)90022-X
- H. T. Lin and S. F. Huang, “Flow and Heat Transfer of Plane Surface Moving in Parallel and Reversely to the Free Stream,” International Journal of Heat and Mass Transfer, Vol. 37, No. 2, 1994, pp. 333-336. doi:10.1016/0017-9310(94)90104-X
- N. Afzal, “Momentum Transfer on Power Law Stretching Plate with Free Stream Pressure Gradient,” International Journal of Engineering Science, Vol. 41, No. 11, 2003, pp. 1197-1207. doi:10.1016/S0020-7225(03)00002-8
- J. X. Lings and A. Dybbs, “Forced Convection over a Flat Plate Submerged in a Porous Medium; Variable Viscosity Case,” ASME, New York, 1987.

