Advances in Microbiology
Vol. 2 No. 2 (2012) , Article ID: 19687 , 16 pages DOI:10.4236/aim.2012.22020
The Poisson Distribution Is Applied to Improve the Estimation of Individual Cell and Micropopulation Lag Phases
1Departamento de Nutrición, Bromatología y Tecnología de los Alimentos, Facultad de Veterinaria, Universidad Complutense, Madrid, Spain
2Servicio Informático de Apoyo a Docencia e Investigación, Universidad Complutense, Madrid, Spain
Email: juaguirr@vet.ucm.es
Received January 24, 2012; revised February 14, 2012; accepted March 16, 2012
Keywords: Individual cells; micropopulations; lag phase; Poisson distribution
ABSTRACT
Many articles dealing with individual cell lag phase determination assume that growth, when observed, comes from one cell. This assumption is not in agreement with the Poisson distribution, which uses the probability of growth in a sample to predict how many samples contain one, two, or some other number of cells. This article analyses and compares different approaches to improve the accuracy of lag phase estimation of individual cells and micropopulations. It argues that if the highest initial load, as predicted by the Poisson distribution, is assigned to the sample with the shortest lag phase, the second highest to the sample with the second shortest lag phase and so on, the resulting lag phase distributions would be more accurate. This study also proposes the use of a robust test, permutation test, to compare lag phase distributions obtained in different situations.
1. Introduction
The measuring of any parameter characterizing the microbial growth is essential for any quantitative microbial risk assessment. Then, to know the microbial lag phase length of viable cells is critical, especially in RTE products, which nature and storing conditions may allow the growth of viable, pathogen or not, bacteria. In the case of populations of thousands or hundreds of viable cells, the lag phase, is quite reproducible if the pre-inoculation and growth conditions are constant. However, the lag phase of populations composed by few cells, or even by only individual cells, is inherently variable. Therefore, it is understandable that researchers [1-9] have paid attention to the distribution of single cells lag times and to the techniques that can measure them. Measuring the lag time of individual cells requires direct microscopic observation [4,8] or techniques to isolate single cells [10]. Cell isolation can be achieved by diluting [2], sorting by flow cytometry [11] or inactivating all organisms except one [9]. When growth is detected in some samples and not in others, it is commonly assumed that growth comes from one cell [12]. The number of samples must always be high for reliable mathematical treatment. It is recommended that approximately 100 samples show growth [13], and this figure must not be a high percentage of the samples. Guillier et al. [5] stated that if 35% of samples show growth, this should not significantly affect individual cell lag phase distributions because at least 80% of samples contain one cell, according to the Poisson distribution function.
“Growth/no growth sampling” has been widely applied to foods and opaque liquids; in the special case of translucent liquids, an apparatus called the Bioscreen C can be used to construct 200 growth curves simultaneously for the same temperature, on the basis of the turbidity resulting from microbial growth. If the specific growth rate (μ) under the experimental conditions is known, the lag phase is determined using the following equations. In the case of translucent liquids analyzed using Bioscreen, the equation is [14]:
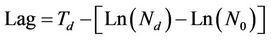 (1)
(1)
where Td is the detection time, i.e. the time needed to reach an arbitrary absorbance (turbidity), Ln(Nd) is the natural logarithm of the number of cells generating such absorbance, Ln(N0) is the natural logarithm of the number of organisms in the inoculum, and μ is the specific growth rate. In the case of opaque samples [6], the equation is:
 (2)
(2)
where Tcount is the time between inoculation and plating of the sample, Ln(xcount) is the natural logarithm of the cell number detected at Tcount, Ln(xinitial) is the natural logarithm of the initial number of bacteria and µ is the specific growth rate.
When a certain percentage of samples does not show growth, the assumption that growth in the other samples is due to one cell contravenes the predictions of the Poisson distribution. Several researchers have used the Poisson distribution to calculate the proportion of growthpositive samples initially containing more than one cell [5,11,15,16]. McKellar and Hawke [17] recognised that one of the limitations of the Bioscreen as a tool to study single cell behaviour is that it is difficult to ensure that the growth in any given positive well arose from a single cell. Earlier, some authors [2,15] performed a series of binary dilutions to have one cell per sample. Francois et al. [2] observed that single cells should be found in wells of Bioscreen microtitre plates where the mean cell number added to each well was less than one. These authors advocate pooling data from the last five binary dilution series to maximise the number of replicate wells; these series contained 0.7812, 0.3906, 0.1951, 0.0977, and 0.0977 cells per well, from a theoretical mean dilution range.
According to the Poisson probability function, if a determined number of occurrences (ρ is expected, then the probability that there are exactly k occurrences (k being a non-negative integer number, k = 0, 1, 2, ∙∙∙) is:
 (3)
(3)
where e is the base of the natural logarithm; k is, in our case, the number of organisms in a sample, and the probability of k is given by the function; ρ is a positive real number, which expresses the average number of cells per sample; and k! is the factorial of k. To highlight the relevance of the data that equation (3) offers, the Table 1 has been built up. This table shows the percentages of samples predicted by equation (3) that would contain a determined number of viable cells as a function of the percentage of samples, in which growth was detected. The average number of cell per sample (m) is also shown in Table 1. This average is calculated by assuming that the number of cell per sample follows a Poisson distribution. Hence, the following equation was used:
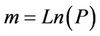 (4)
(4)
where P is the probability of there is not any viable cell in a sample. Applying equation (3) to the data of Francois et al. [2], with an average number of cells per sample of 0.78, indicates that 65% of the positive samples contain one cell, 25.3% contain two, 6.6% three and 1.3% four. These figures suggest that the estimated lag phase determinations for individual cells will have a certain error. Indeed, Baranyi et al. [18] affirmed that the greater the Poisson parameter (ρ, average number of cells per sample), the less accurately equations (1) and (2) estimate the distribution of the single cell lag time. If samples are considered to contain only one cell, the value of Ln(N0) in equation (1) and Ln(Xinitial) in equation (2) is zero. However, if the predictions of the Poisson function are applied, we have to assume that some samples contain two, three or more cells, which is an undisputed fact in most real samples. In this case, Ln(N0) and Ln(Xinitial) are positive numbers that lengthen the lag phase of such samples.
The aim of this study is to compare the individual cell and/or micropopulation lag phase distributions obtained by assuming that all samples with growth contain one

Table 1. Percentage of samples with a determined number of cells, as predicted by Poisson function (equation (3)).
cell, with the distributions obtained by assuming a different number of cells per sample according to the Poisson distribution function.
2. Material and Methods
2.1. Simulation
A simulation was generated considering a different average number of cells per sample (0.2 - 2.0). To create the simulation, 100 values of lag phases were randomly generated by assigning them values from 40 to 180 arbitrary time units, following a gamma distribution with the following parameters: shape = 5.5, scale = 16.5, mean = 91.7 and standard deviation = 29.4. A specific growth rate (μ) of 0.0693 h–1 was also considered. The resulting distribution data are those of Scenario I (see next section).
2.2. Scenarios
Four scenarios were used to calculate the lag phase distributions: Scenario I assumes that all samples contain one cell. Scenarios II-IV use the Poisson distribution function to assign a number of cells to each sample. In Scenario II, the sample with the shortest lag phase contains the highest number of cells, according to the average number of cells per sample and the Poisson table [19], the sample with the second shortest lag contains the second highest number of cells, and so on. In Scenario III, the number of cells is randomly distributed among samples, regardless of the lag phase length. Scenario IV is calculated like Scenario II, except that all samples with more than one cell are not considered. From the data of Scenario I, lag phases were recalculated according to the assumptions of Scenarios II, III and IV and the corresponding distributions were obtained.
2.3. Statistical Analysis
Pairwise comparisons of the variances of lag phase distributions were carried out using a permutation test to analyse homogeneity of the two variances; this bilateral test assumes that the variances ratio is one. Permutation tests are non-parametric significance tests based on permutation resampling without replacement, with observed lag times drawn at random from the original data and reassigned to the two groups being compared. The distribution of possible variance ratios is calculated for all samples assuming the null hypothesis of homogeneity, and the observed ratio is positioned along this distribution. Values falling outside the main distribution rarely occur by chance and therefore give evidence of heterogeneity of variances [20]. Since our study involves multiple comparisons of several groups, a p-value correction must be applied in order to minimise the probability of rejecting a true hypothesis. The Holm-Bonferroni p-value correction [21] was applied. This correction is less conservative than those of Bonferroni and Sidak [22], which are also applied in the permutation test program described in appendix A.
A permutation test routine including a multiple comparison test was programmed using R language [23], which is described in Annex 1.
2.4. Application of Scenarios to Experimental Data
To check how well the simulations mimic the reality, the four scenarios were applied to the lag phases of Enterococcus faecalis, Pseudomonas fluorescens, Salmonella enterica serovar Enteritidis and Listeria innocua subjected to different irradiation treatments in tryptic soy broth (TSB) and cooked ham and subsequently incubated at different temperatures (experimental data from Aguirre et al. [9]). Lag phases were estimated according to equations (1) and (2) after determining the percentage of samples without growth and considering the Poisson function predictions and the scenarios above described.
3. Results
3.1. Simulation
Figure 1(a) shows the increase in the mean lag and Figures 1(b) and (c) show, respectively, the decrease in the standard deviation and the coefficient of variation as a function of the average number of cells per sample. The dashed line in Figure 1 shows the mean and standard deviations of the data in Scenario I. As expected, the greater the number of cells per sample is, the larger the difference between the mean and standard deviation of Scenario I data and those of the others. The distributions of Scenario III were not considered further because the averages were identical to those of Scenario II and their standard deviations were very close to those of Scenario I (data not shown).
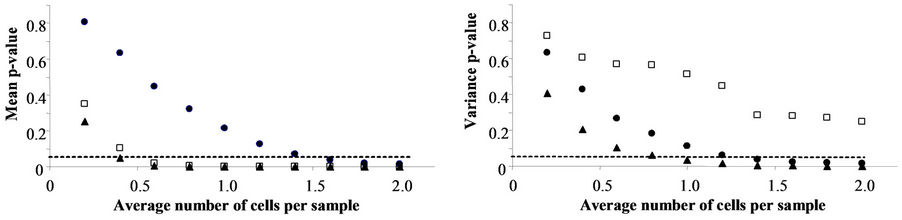
Comparison of the distributions obtained in Scenarios I and II, I and IV and II and IV (Figure 2) shows that the higher the more probable number per sample is, the smaller the p value for comparisons of the mean and standard deviation, according to the permutation test. Significant differences (α < 0.05) were found among the three comparisons for the mean and between Scenarios I and II and I and IV for the standard deviation.
3.2. Application of Scenarios to Experimental Data
Table 2 summarises the experimental data, including the expected inactivation according to the irradiation applied, the average number of surviving cells per sample and the
 (a)
(a)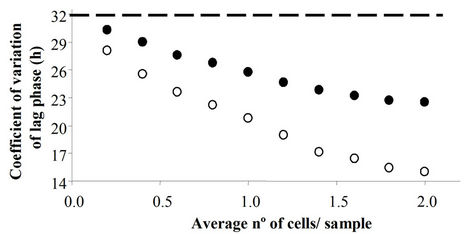 (b)
(b)
Figure 1. Effect of the average number of cells per sample on the mean (a), standard deviation (b) and coefficient of variation (Sd*100/mean, C) of lag phase distribution in a model system assuming that lag phases follow a gamma distribution and that m = 0.0693 h−1. Dashed lines represent the mean, standard deviation and coefficient of variation assuming that all samples contain one cell (Scenario I). Solid symbols show the results assuming a variable number of cells per sample, and assuming that the sample with the shortest lag phase contains the highest number of cells, the sample with the second shortest lag contains the second highest number, and so on, according to the Poisson distribution function (Scenario II). Empty symbols represent the results following the assumptions in (Scenario II) but including only samples with one cell (Scenario IV).
 (a) (b)
(a) (b)
Figure 2. Comparison by permutation test of means (a) and variances (b) of lag phase distributions obtained when all samples with growth are assumed to contain one cell (Scenario I) with those obtained under other assumptions (Scenarios II and IV). The solid circles show the comparison between (Scenarios I and II), in which samples with growth are assumed to contain one or more cells according to the truncated Poisson distribution, and assuming that the sample with the shortest lag phase is supposed to have the highest inocula. The solid triangles show the comparison between (Scenarios I and IV), which makes the same assumptions as (Scenario II) but excludes samples containing more than one cell. Empty squares show the comparison between (Scenarios II and IV). Dashed lines represent the α-value = 0.05. Data below the line indicate significant differences.
characteristics of the distributions (mean, standard deviation and coefficient of variation) for each substrate, treatment (Aguirre et al. [9]) and scenario. Scenario III was not considered for the reasons mentioned above. As in the simulations, analysis of the experimental data showed that the mean lag phase when growth is assumed to be due to a variable number of cells (Scenario II) was equal to, or higher than, the mean when growth is assumed to be due to a single cell (Scenario I). In contrast, the standard deviations in Scenario II were always lower than those in Scenario I, except in the case of Salmonella Enteritidis growing in ham at 7˚C after no treatment.
The permutation test was used to compare the distributions between Scenarios I and II, I and IV and II and IV.
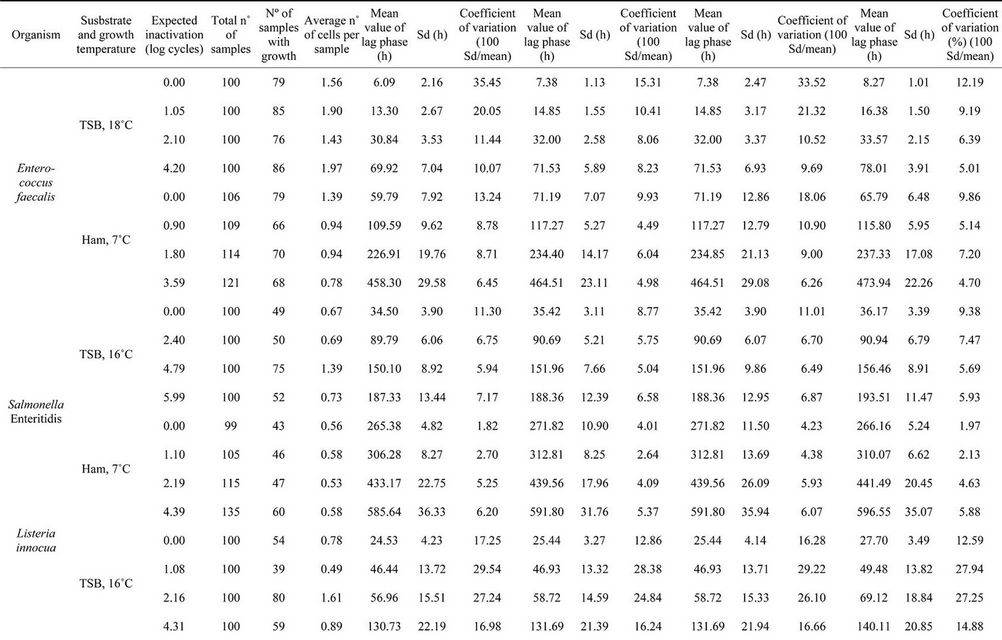
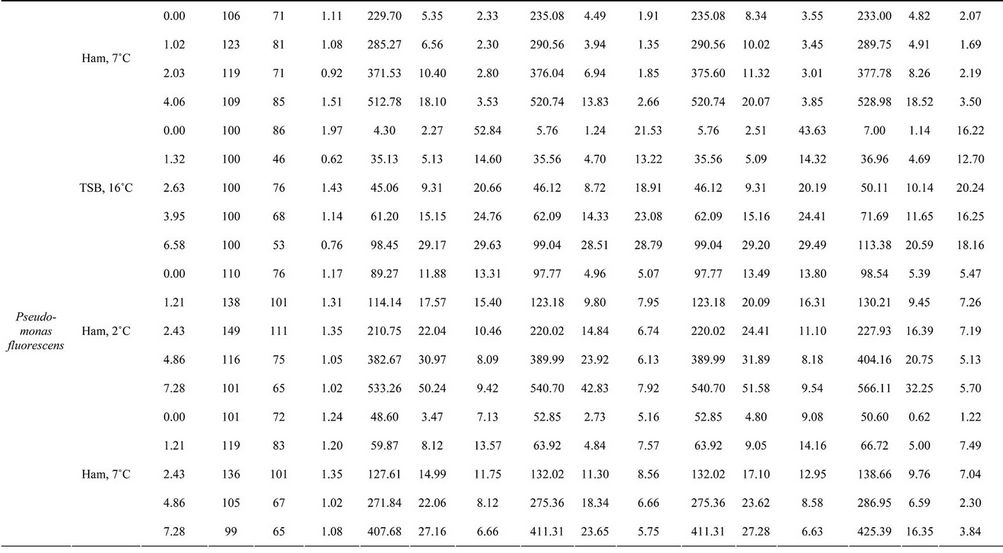
Table 2. Lag phases of organisms surviving treatment on ham and TSB, as calculated using four scenarios. Explanation on scenarios is in legend of Figure 1.
Several significant differences (α < 0.05) were found and in order to clarify the reasons of such differences, the average number of cells per sample and the specific growth rate were plotted (Figure 3).
4. Discussion
Obviously, to consign to oblivion the Poisson function of distribution, when growth is observed in a determined percentage of homogeneous samples, and consider that this growth comes from one viable cell, is erroneous because the probability of that a significant number of samples contains more than one cell is very high (see Table 1); obviously, the higher the average number of cells per sample is, the higher the probability of finding
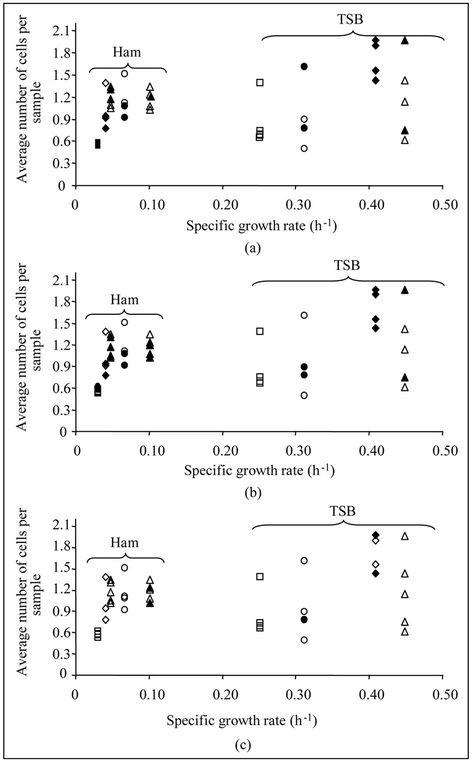
Figure 3. Comparison of lag phase distributions between Scenarios I and II (a), I and IV (b), and II and IV (c) using the permutation test. Empty symbols indicate that there are no significant differences (α > 0.05) between distributions. Solid symbols indicate significant differences (α < 0.05). Data were taken from Aguirre et al. (2011) and correspond to Listeria innocua (circles), Pseudomonas fluorescens (triangles), Salmonella Enteritidis (squares) and Enterococcus faecalis (diamonds).
samples with more than one cell.
In order to determine more accurately the lag phase, we propose to assume that the sample with the shortest lag phase contains the highest number of cells, according to the Poisson distribution, the sample with the second shortest contains the second highest number of cells, and so on (Scenario II). This assumption is based on the fact that higher inocula need less number of duplications (i.e. less time) to reach a determined number of cells (Td or Tcount in equations (1) and (2), respectively) and then, lag is actually longer than if the growth had been generated by only one cell. Furthermore, it is known that the lag phase of individual cells is variable [1,7,9] and, logically, it is more likely to find a fast cell in starting the growth in samples that contain higher number of cells and, obviously, lag phase of these samples must be shortened because of the “fast” cells. Pin and Baranyi [7], working with single cells and micropopulations, stated that samples with low initial number of cells, showed longer lag times—in average—than those initiated with more cells. All these reasonings support the starting hypothesis.
The greater the number of cells per sample is, the larger the difference between the mean and standard deviation of lag phase distributions (Figure 1). Then, when individual cell lag phases are determined, larger errors are expected as the number of cells per sample increases, confirming the Baranyi et al. [18] statement. In other words, in practical situations, the greater the number of samples with microbial growth is, the greater the expected errors in individual cell lag phase estimation. Figure 2 corroborates this finding since the higher the average number of cells per sample is, the more probably is to find significant differences (α < 0.05) between the distributions of all scenarios analyzed.
Remarkable differences between Scenarios I and IV were observed in both the mean and the standard deviation (Figure 1). It is important to remember that in this case, lag phase data, when one cell per sample is assumed (Scenario I), are compared with the lag phase data of cells with longer lags (IV), which are more likely to contain, actually, one cell. Samples with shorter lag phases are ignored in Scenario IV and, therefore, data from fast cells growing alone are not included. Then, the lag phase average is always biased to long times in this scenario.
Scenarios II and III should model the experimental data more closely than Scenario I because equations (1) and (2), used to calculate the lag phase, reduce the time to reach a given microbial concentration (Td or Tcount) by the time that the initial cell number takes to reach the given concentration {[(Ln(Nd) – Ln(N0)]/μ] or [(Ln(Xcount) – Ln(Xinitial)]/μ]}. This is true regardless of the variability in growth rate observed in the first divisions of a cell [4], because this variability seems to be randomly distributed [24]. Recalculating the lag phases of samples more likely to contain more than one cell is easily accomplished by substituting N0 or Xinitial in equations (1) and (2), respectively, by the number of cells predicted by the Poisson function. When the lag phase is determined by Bioscreen or in food, assuming that all samples contain one cell, the sample with the shortest lag phase is most likely to contain the highest inoculum, and samples with the longest lag phases are most likely to contain only one cell. Based on this reasoning, if more accurate data on initial microbial concentration can be obtained, the quality of lag phase estimation will improve, although these estimations are not absolutely accurate due to the intrinsic cell variability. Actually, one cell may have a short lag phase, even shorter than that of a micropopulation of two medium or long lag phase cells, even considering that one cell have to duplicate once more than two cells to reach the same number of daughter cells and this duplication time is, of course, considered by equations (1) and (2) when calculating lag phases.
The analysis of the experimental data of Table 2 shows that the mean lag phase, when growth is assumed to be due to a variable number of cells (Scenario II), was higher than the mean when growth is assumed to be due to a single cell (Scenario I). Furthermore, the lower the lag phases of Scenario I were, the greater the percentage of increase (Table 2). This means that considering that all samples contain one cell in optimum growth conditions or in healthy cells, which imply short lag phases, generates relevant inaccuracies, while the lag phase determination of injured cells and at suboptimal growth conditions, the error may even become negligible (Table 2). These statements are only pertinent for the lag phase average because if we consider the transformation from Scenario I to Scenario II, data to data, it is evident that short lag phases estimated according to Scenario I are transformed in longer ones, probably in a non realistic way. An example is shown in Tables 3 and 4, which show the lag phases of non-radiated and irradiated (2 kGy) Enterococcus faecalis in TSB at 18˚C, respectively (data of distributions are shown in Table 2). The analysis of the Table 3 data allows to affirm that the recalculation of lag phases according to Scenario II, ascribing the highest number of cells to the sample with the shortest lag and the second highest number of cells to the second shortest, etc., result in a too long lag phases for such samples, which hardly correspond to a samples with five cells instead one (the first two data of the left columns of the Table 3). The analysis of Table 4 data drives to the same reasoning, although the lengthening of lag phases due to the irradiation minimizes the differences. In contrast, the standard deviations in Scenario II were almost always lower than those in Scenario I (Table 2), which means a lower dispersion of data and, presumably, a
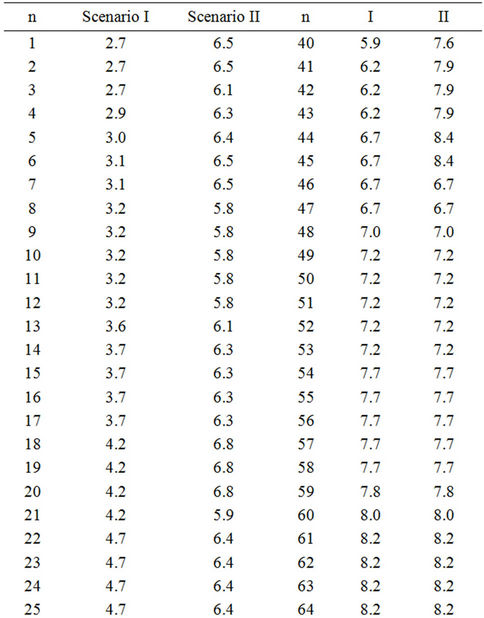
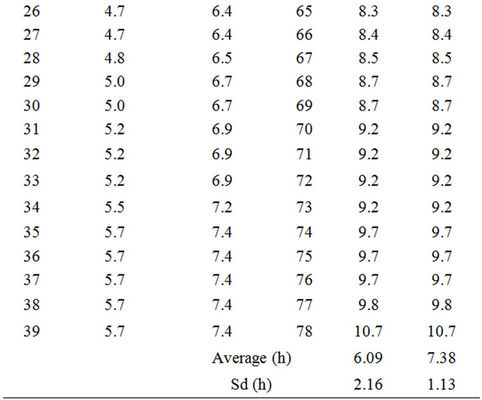
Table 3. Lag phases of non-radiated Enterococcus faecalis in TSB at 18˚C calculated by equation (1) considering a constant μ of 0.409 and assuming: Scenario I: All samples contain 1 cell; Scenario II: The sample in column “Scenario I” with the shortest lag phase contains the highest inoculum, the second shortest, the second highest, and so on. Number of cells per sample was estimated according to the Poisson distribution considering that the average number of cells per sample was 1.56 (Table 2). Then, according to the Poisson function of distribution (equation (3)), the first two samples must contain five cells, the next five samples four cells, the next thirteen samples three cells, the next twenty six samples two cells and the last thirty three samples one cell. n. Number of sample, decreasingly ordered according to the Scenario I lag phase.
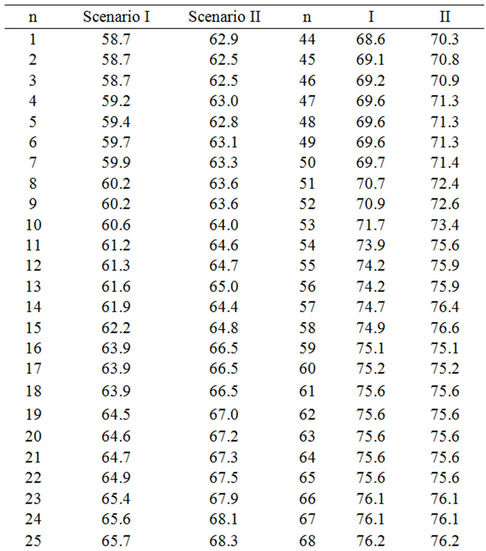
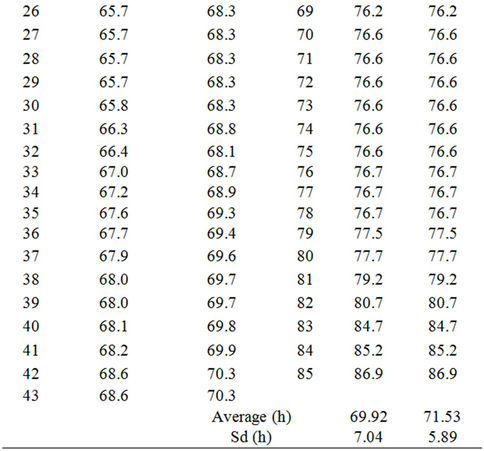
Table 4. Lag phases of Enterococcus faecalis irradiated with 2 kGy in TSB at 18˚C calculated by equation (1) considering a constant μ of 0.409 and assuming: Scenario I: All samples contain 1 cell; Scenario II: The sample in column “Scenario I” with the shortest lag phase contains the highest inoculum, the second shortest, the second highest, and so on. Number of cells per sample was estimated according to the Poisson distribution considering that the average number of cells per sample was 1.97 (Table 2). Then, according to the Poisson function of distribution (equation (3)), the first sample must contain six cells, the next three samples five cells, the next nine samples four cells, the next eighteen samples three cells, the next twenty seven samples two cells and the last twenty seven samples one cell. n. Number of sample, decreasingly ordered according to the Scenario I lag phase.
more accurate lag phase determinations when applying the Scenario II, which means that, in spite of the above discussed arguments, the average of the recalculated distribution (Scenario II) must be more realistic than that of Scenario I.
The robust permutation test (see Annex 1) is proposed to compare lag phase distributions. When this test was applied to the experimental data of Aguirre et al. [9], several significant differences (α < 0.05) were found between Scenarios I and II, I and IV and II and IV. From Figure 3, it may be deduced that the higher the average number of cells per sample was, the greater the probability that there would be significant differences in distributions between Scenario I and II or between I and IV. This is consistent with the predictions of the simulation generated in this study. The influence of the specific growth rate on the distributions is less clear.
5. Conclusion
To estimate lag phase, the assumption that growth comes from one cell in all samples when a certain percentage of them does not show microbial growth contradicts the Poisson distribution function. Taking into account the percentage of samples showing microbial development, the Poisson function allows ascribing higher inocula to the samples with shorter lag phases. Considering Poisson-based predictions of the number of cells per sample, instead of considering that all samples contain one cell, the accuracy of the average lag phase determinations of micropopulations will be improved. In fact, the more samples there are that contain more than one cell, the greater the improvement will be. This improvement is likely to be statistically significant mainly in cases where the average number of cells per sample is relatively high.
6. Acknowledgements
The authors gratefully acknowledge the support of the Ministerio de Educación y Ciencia (Spain), Program Consolider CARNISENUSA CSD2007-0016 and AGL- 2010-16598. We thank Armando Chapin Rodríguez for his assistance in the manuscript writing.
REFERENCES
- P. J. Stephens, J. A. Joynson, K. W. Davies, R. Holbrook, H. M. Lappin-Scott and T. J. Humphrey, “The Use of an Automated Growth Analyser to Measure Recovery Times of Single Heat-Injured Salmonella Cells,” Journal of Applied Microbiology, Vol. 83, No. 4, 1997, pp. 445-455. doi:10.1046/j.1365-2672.1997.00255.x
- K. Francois, F. Devlieghere, A. R. Standaert, A. H. Geeraerd, J. F. Van Impe and J. Debevere, “Modelling the Individual Cell Lag Phase. Isolating Single Cells: Protocol Development,” Letter of Applied Microbiology, Vol. 37, No. 1, 2003, pp. 26-30. doi:10.1046/j.1472-765X.2003.01340.x
- A. Metris, S. M. George, M. W. Peck and J. Baranyi, “Distribution of Turbidity Detection Times Produced by Single Cell-Generated Bacterial Populations,” Journal of Microbiological Methods, Vol. 55, No. 3, 2003, pp. 821- 827. doi:10.1016/j.mimet.2003.08.006
- A. Elfwing, Y. LeMarc, J. Baranyi and A. Ballagi, “Observing Growth and Division of Large Numbers of Individual Bacteria by Image Analysis,” Applied and Environmental Microbiology, Vol. 70, No. 2, 2004, pp. 675- 678. doi:10.1128/AEM.70.2.675-678.2004
- L. Guillier, P. Pardon and J. C. Augustin, “Influence of Stress on Individual Lag Time Distributions of Listeria monocytogenes,” Applied and Environmental Microbiology, Vol. 71, No. 6, 2005, pp. 2940-2948. doi:10.1128/AEM.71.6.2940-2948.2005
- M. D’Arrigo, G. D. Garcia de Fernando, R. Velasco de Diego, J. A. Ordonez, S. M. George and C. Pin, “Indirect Measurement of the Lag Time Distribution of Single Cells of Listeria innocua in Food,” Applied and Environmental Microbiology, Vol. 72, No. 4, 2006, pp. 2533- 2538. doi:10.1128/AEM.72.4.2533-2538.2006
- C. Pin and J. Baranyi, “Kinetics of Single Cells: Observation and Modeling of a Stochastic Process,” Applied and Environmental Microbiology, Vol. 72, No. 3, 2006, pp. 2163-2169. doi:10.1128/AEM.72.3.2163-2169.2006
- G. W. Niven, J. S. Morton, T. Fuks and B. M. Mackey, “Influence of Environmental Stress on Distributions of Times to First Division in Escherichia coli Populations, as Determined by Digital-Image Analysis of Individual Cells,” Applied and Environmental Microbiology, Vol. 74, No. 12, 2008, pp. 3757-3763. doi:10.1128/AEM.02551-07
- J. S. Aguirre, M. R. Rodriguez and G. D. Garcia de Fernando, “Effects of Electron Beam Irradiation on the Variability in Survivor Number and Duration of Lag Phase of Four Food-Borne Organisms,” International Journal of Food Microbiology. Vol. 149, No. 3, 2011, pp. 236-246. doi:10.1016/j.ijfoodmicro.2011.07.003
- I. A. Swinnen, K. Bernaerts, E. J. Dens, A. H. Geeraerd and J. F. Van Impe, “Predictive Modelling of the Microbial Lag Phase: A Review,” International Journal of Food Microbiology. Vol. 94, No. 2, 2004, pp. 137-159. doi:10.1016/j.ijfoodmicro.2004.01.006
- J. P. Smelt, G. D. Otten and A. P. Bos, “Modelling the Effect Of Sublethal Injury on the Distribution of the Lag Times of Individual Cells of Lactobacillus plantarum,” International Journal of Food Microbiology, Vol. 73, No. 2-3, 2002, pp. 207-212.
- A. Metris, S. M. George and J. Baranyi, “Use of Optical Density Detection Times to Assess the Effect of Acetic Acid on Single-Cell Kinetics,” Applied and Environmental Microbiology, Vol. 72, No. 10, 2006, pp. 6674-6679. doi:10.1128/AEM.00914-06
- BACANOVA, “Final Report on the European Project QLRT-2000-01145: Optimisation of Safe Food Processing Methods Based on Accurate Characterisation of Bacterial Lag Time Using Analysis of Variance Techniquesm,” BACANOVA Consortium, European Commission, Brussels, 2005.
- J. Baranyi and C. Pin, “Estimating Bacterial Growth Parameters by Means of Detection Times,” Applied and Environmental Microbiology, Vol. 65, No. 2, 1999, pp. 732- 736.
- R. C. McKellar and K. Knight, “A Combined DiscreteContinuous Model Describing the Lag Phase of Listeria monocytogenes,” International Journal of Food Microbiology, Vol. 54, No. 3, 2000, pp. 171-180. doi:10.1016/S0168-1605(99)00204-4
- T. P. Robinson, O. O. Aboaba, A. Kaloti, M. J. Ocio, J. Baranyi and B. M. Mackey, “The Effect of Inoculum Size on the Lag Phase of Listeria monocytogenes,” International Journal of Food Microbiology, Vol. 70, No. 1-2, 2001, pp. 163-173. doi:10.1016/S0168-1605(01)00541-4
- R. C. McKellar and A. Hawke, “Assessment of Distributions for Fitting Lag Times of Individual Cells in Bacterial Populations,” International Journal of Food Microbiology, Vol. 106, No. 2, 2006, pp. 169-175. doi:10.1016/j.ijfoodmicro.2005.06.018
- J. Baranyi, S. M. George and Z. Kutalik, “Parameter Estimation for the Distribution of Single Cell Lag Times,” Journal of Theoretical Biology, Vol. 259, No. 1, 2009, pp. 24-30. doi:10.1016/j.jtbi.2009.03.023
- I. Espejo, F. Fernández, M. A. López, M. Muñoz, A. M. Rodríguez, A. Sánchez and C. Valero, “Estadística Descriptiva y Probabilidad,” 3rd Edition, U.d.C., Cadiz, 2006. http://knuth.uca.es/repos/l_edyp/pdf/-febrero06/lib_edyp.apendices.pdf
- T. Hesterberg, D. S. Moore, S. Monaghan, A. Clipson, R. Epstein and G. P. McCabe, “Bootstrap Methods and Permutation Tests,” In: W. H. McCabe, Ed., Introduction to the Practice of Statistics (5th Edition), Freeman & Co., New York, 2005, pp. 14.1-14.70.
- S. Holm, “A Simple Sequentially Rejective Multiple Test Procedure,” Scandinavian Journal of Statistics, Vol. 6, 1979, pp. 65-70.
- H. Abdi, “Bonferroni and Sidák Corrections for Multiple Comparisons,” In: C. S. Neil Salkind, Ed., Encyclopedia of Measurement and Statistics, Dallas, Thousand Oaks, 2007, pp. 103-107.
- R Version 2.72, “Language and Environment for Statistical Computing,” The R Foundation for Statistical Computing, 2008.
- C. Pin and J. Baranyi, “Single-Cell and Population Lag Times as a Function of Cell Age,” Applied and Environmental Microbiology, Vol. 74, No. 8, 2008, pp. 2534- 2536. doi:10.1128/AEM.02402-07
Appendix A
#####################################################
# PROGRAM PERMUTATION_VARIANCE_RATIO_TEST v2.0 #
#####################################################
# Authors: María del Carmen Bravo and Juan Aguirre - November 2011
# This R program (http://cran.es.r-project.org/) applies the permutation
# test to the null hypothesis of homogeneity of two variances.
# It applies a multiple test procedure to comparisons of several variance
# pairs. To minimize the probability of rejecting a true hypothesis# Bonferroni and Sidak p-value corrections, as well as the less conservative
# Holm-Bonferroni corrections, are applied to the p-values.
# The lag-time distribution of single cells of different microorganisms is
# analysed. For each microorganism, the analysis is carried out using 3, 4, or
# 5 dose or scenario groups. By default, the number of variance pair
# comparisons in these cases are 3, 6 and 10, respectively.
# All tests are bilateral (alternative hypothesis is nonhomogeneity).
# Extension to unilateral tests (alternative hypothesis is that one variance
# is larger), and to different numbers of doses or scenarios, is possible.
# Also the number of comparisons may be reduced.
# Permutation test:
# ----------------# The homogeneity of two variances test is equivalent to the variance
# ratio test, with the null hypothesis stating that the ratio of variances
# is equal to 1.
# For two dose or scenario groups, the variances of the lag-time of both
# groups and their ratio (variance_ratio) are computed.
# For a number of times, n_permutations:
# - Lag-time observations are randomly distributed into the two dose
# or scenario groups. Original dose or scenario sizes are maintained.
# - Variances of both groups and their ratio are computed.
# A distribution of the variance ratios is obtained.
# If the variance_ratio value is an anomalous value of this distribution# then the hypothesis of homogeneity of variances is rejected.
# A histogram of the variance ratio distribution is generated.
# Bonferroni and Sidak p-value corrections:
# ----------------------------------------# The output of each homogeneity of variances test is its p-value and
# the corrected Sidak and Bonferroni p-values that take into account the
# number of variance pair comparisons. The Bonferroni correction is the
# test p-value multiplied by the number of comparisons. This value
# must be compared to a multiple significance level alpha.
# Holm-Bonferroni p-value corrections:
# -----------------------------------# p-values of homogeneity of variance tests are ordered from lower to higher.
# These values are compared to alpha/n_comparisons, alpha/(n_comparisons-1)
# alpha/(n_comparisons-2),..., alpha, respectively. The p-values must be lower
# than this second set of values to be significant with a multiple
# significance level alpha.
# References:
# ----------# Abdi, H. 2007. Bonferroni and Sidák corrections for multiple comparisons.
# In: N.J. Salkind (ed.) Encyclopedia of Measurement and Statistics, Thousand # Oaks, CA: Sage. pp. 103-107
# Hesterberg, T., Moore, D.S., Monaghan, S., Clipson, A., Epstein, R.. McCabe, # G.P., 2005, Bootstrap Methods and Permutation Tests. In: Moore, D.S. &
# McCabe, G.P.: Introduction to the Practice of Statistics, Fifth Ed., W.H.
# Freeman & Co. pp. 14.1-14.70.
# Holm, S., 1979. A simple sequentially rejective multiple test procedure.
# Scandinavian Journal of Statistics, 6, 65-70.
# R version 2.7.2, 2008. R: A Language and Environment for Statistical
# Computing. Reference Index. The R Foundation for Statistical Computing.
# ISBN 3-900051-07-0.
# To run the program in R: Mouse-selection of several sentences + F5
#####################################################
# Function definitions #
#####################################################
# The function definitions part of the program is executed once.
# permutation_test function definition.
# g1, g2: ordinal numbers identifying dose or scenario groups.
permutation_test <- function(g1,g2) {
assign("k",k+1,envir=.GlobalEnv)
lag2g<-LAG[Key==keys[g1] | Key==keys[g2]]
ng1<-n_groups[g1]
ng2<-n_groups[g2]
n1<-ng1
n11<-ng1+1
n2<-ng1+ng2 variance_ratio<-var_groups[g1]/var_groups[g2]
s_variance_ratio<-numeric(n2)
s_variance_ratio<-variance_ratio
for (i in 1:(n_permutations-1)) {
s_lag2g<-sample(lag2g)
s_variance_ratio<-c(s_variance_ratio,var(s_lag2g[1:n1])/var(s_lag2g[n11:n2]))
}
position<-length(s_variance_ratio[s_variance_ratio<=variance_ratio])
# p_inf: left tail estimated probability for variance_ratio value
p_inf<-position/n_permutations
p_sup<-1-p_inf
p_value<-print_results (g1,g2,variance_ratio,p_inf,p_sup)
# If the user does not want to see the histograms, add the # symbol as the
# first character in the following two sentences.
win.graph()
histogram(s_variance_ratio,g1,g2)
p_value
}
# print_results function definition print_results <- function (g1,g2,coc,p_inf,p_sup) {
cat ('------------------- Permutation test ---------------------',"\n")
cat('Groups:', keys[g1],keys[g2],"\n")
cat('Variance ratio:',coc,"\n")
# p_value: p-value for the two-tailed test
if (1/n_permutations < p_inf & p_inf <= 0.5) p_value <- p_inf*2
if (0 < p_sup & p_sup < 0.5) p_value <- p_sup*2
# p_bon, p_sidak: corrected Bonferronni and Sidak p_values for
# n_comparisons tests
if ((1/n_permutations p_bon <- p_value*n_comparisons p_sidak <- 1-(1-p_value)^n_comparisons } if (p_inf==1/n_permutations | p_sup==0) { p_value <- 1/n_permutations p_bon <- 1/n_permutations p_sidak <- 1/n_permutations cat('Two-tailed p_value lower than',1/n_permutations,"\n") cat('Bonferroni corrected p_value lower than',1/n_permutations) cat("\n",'Sidak corrected p_value lower than',1/n_permutations,"\n") } if (p_value > 1/n_permutations) cat('Two-tailed p_value:',p_value,"\n") if (1/n_permutations < p_value & p_value < alpha) { cat('Bonferroni corrected p_value:',p_bon,"\n") cat('Sidak corrected p_value:',p_sidak,"\n") } if (min(p_bon,p_sidak)>alpha ) { cat('** Non significant differences between variances **',"\n")} if (min(p_bon,p_sidak) {cat ('** Variances of doses groups are different **',"\n")} cat ('----------------------------------------------------------',"\n") p_value } # histogram function definition histogram <-function (x,g1,g2) { graph_name<-paste(file_name,sheet_name,'Groups:',keys[g1],'and',keys[g2]) hist(x, main = graph_name) } ##################################################### # End of function definitions # ##################################################### ##################################################### # Main program # ##################################################### # Program parameters: # ------------------# alpha: Multiple significance level for n_comparisons of permutation # test of the homogeneity of two variances. Usual value: 0.05 # n_permutations: Number of permutations. Usual value: 10000 # file_name: Name of the Excel file with the input data # sheet_name: Name of the Excel sheet with the input data # Name of columns: Key LAG # Key refers to treatment names (doses or scenarios) # LAG refers to LAG-time # groups_number: Number of dose or scenario groups. # Possible values: 3, 4, 5 # n_comparisons: Number of pairwise comparisons. Values: 3, 6, 10 # for respective group_number values of 3, 4, 5 # Its value is used for p_value corrections # keys: group_number dimension vector with dose or scenario group names # digits: Number of digits for output of numerical values # output_file_name: Name of output file when user wants program output # diverted to a file instead of to the R terminal # This main program must be executed once for all variance comparisons of # lag-time distribution for each microorganism # IMPORTANT NOTE: The user must assign values to these program parameters # --------------alpha <- 0.05 n_permutations <- 10000 # file_name and sheet_name are only necessary for the output, to identify # results file_name <- 'file-name.xls' sheet_name <- 'sheet-name' groups_number <- 3 # Give the dose or scenario names in the case of groups_number equal # to 3, 4 or 5. Names are case-sensitive. if (groups_number == 3) keys <- c('A','B','C') if (groups_number == 4) keys <- c('A','B','C','D') if (groups_number == 5) keys <- c('A','B','C','D','E') # Output: # ------# Program output can be diverted to the R terminal (default) or to a file. # If output is written to a file, specify the name of the file # (for example: output_file_name="c:/output_files/Lag_ HAM.txt") # and run the following two sentences without the # symbol. # output_file_name="complete-file-name" # sink(file = output_file_name, append = TRUE, type = "output",split = FALSE) # the append = TRUE option means that the output will be appended # to the file; otherwise, it will overwrite the contents of the file. # If during an R session you want to divert output to the R terminal# run the next sentence without the # symbol. # sink(file=NULL) ################### Data entry #################### # 1. Open the Excel file file_name, sheet sheet_name # 2. Select the columns Key and LAG (names are case-sensitive) # 3. Click menu option Edit --> Copy (or CTRL + C ) # 4. Execute the next two R sentences # If the decimal point is written as a comma in your input data, read # the note at the end of the program data<- read.table("clipboard",header=T) attach(data) # digits controls the number of digits to print # when printing numeric values. # options(digits=5) ################## Running the analysis ############## # User has two options: # 1) Select all sentences through to the end of the program and execute them # 2) Execute the following command blocks as appropriate if (groups_number == 3) n_comparisons <- 3 if (groups_number == 4) n_comparisons <- 6 if (groups_number == 5) n_comparisons <- 10 cat('Input data: File ', file_name ,', sheet ', sheet_name,"\n") cat('Number of doses or scenario groups:',groups_number,"\n") cat('Number of comparisons:',n_comparisons,"\n") cat('Multiple significance level:', alpha,"\n") g1<-Key[Key==keys[1]] ng1<-length(g1) g2<-Key[Key==keys[2]] ng2<-length(g2) g3<-Key[Key==keys[3]] ng3<-length(g3) n_groups<-c(ng1,ng2,ng3) var1<-var(LAG[Key==keys[1]]) var2<-var(LAG[Key==keys[2]]) var3<-var(LAG[Key==keys[3]]) var_groups<-c(var1,var2,var3) # Running this block is required for groups_number > 3, though it can be run # for any value of groups_number. if (groups_number>3) { g4<-Key[Key==keys[4]] ng4<-length(g4) n_groups<-c(n_groups,ng4) var4<-var(LAG[Key==keys[4]]) var_groups<-c(var_groups,var4) } # Running this block is required for groups_number = 5, though it can be run # for any value of groups_number. if (groups_number==5) { g5<-Key[Key==keys[5]] ng5<-length(g5) n_groups<-c(n_groups,ng5) var5<-var(LAG[Key==keys[5]]) var_groups<-c(var_groups,var5) } # Continue running the program std_groups <- sqrt(var_groups) cat('Names of doses or scenario groups:', keys,"\n") cat('Variances:', var_groups,"\n") cat('Standard deviations:', std_groups,"\n") # k: Initialization of the number of comparisons # performed. User should not # change this value # k increments its value by one each time #permutation_test function is run k<-0 c1<-numeric(n_comparisons) c2<-numeric(n_comparisons) p_values<-numeric(n_comparisons) # Execution of the permutation_test function as permutetion_test(g1,g2)# where g1, g2: ordinal numbers identifying dose or scenario groups. # n_comparisons permutation_test definition functions must be run. p<-permutation_test(1,2); c1[k]<-1; c2[k]<-2; p_values[k]<-p p<-permutation_test(1,3); c1[k]<-1; c2[k]<-3; p_values[k]<-p p<-permutation_test(2,3); c1[k]<-2; c2[k]<-3; p_values[k]<-p # Running this block is required for groups_number > 3, though it can be run # for any value of groups_number. if (groups_number>3) { p<-permutation_test(1,4); c1[k]<-1; c2[k]<-4; p_values[k]<-p p<-permutation_test(2,4); c1[k]<-2; c2[k]<-4; p_values[k]<-p p<-permutation_test(3,4); c1[k]<-3; c2[k]<-4; p_values[k]<-p } # Running this block is required for groups_number = 5, though it can be run # for any value of groups_number. if (groups_number==5) { p<-permutation_test(1,5); c1[k]<-1; c2[k]<-5; p_values[k]<-p p<-permutation_test(2,5); c1[k]<-2; c2[k]<-5; p_values[k]<-p p<-permutation_test(3,5); c1[k]<-3; c2[k]<-5; p_values[k]<-p p<-permutation_test(4,5); c1[k]<-4; c2[k]<-5; p_values[k]<-p } # Continue running the program: # -to control possible errors in k value and # -to perform tests that apply Holm-Bonferroni p-value corrections if (k>n_comparisons) { cat ('******* ERROR *******',"\n") cat ('The number of permutation tests run is greater than', n_comparisons) cat ("\n",'Start the running of the program from sentence k<-0') } # ord_p: test p-values in order of increasing value ord_p <- order(p_values) # alpha_i: Holm-Bonferroni significance level for the ith test for a multiple # significance level alpha alpha_i<-c(alpha/n_comparisons:1) C<-matrix(c(c1[ord_p],c2[ord_p],p_values[ord_p],alpha_i),nrow=n_comparisons) aux<-numeric(n_comparisons) for (i in 1:n_comparisons) { aux[i]<-0 if (C[i,3]< C[i,4]) aux[i]<-1 } CC<-matrix(c(C,aux),nrow=n_comparisons) #L: number of significance tests L <-sum(CC[,5]) #CCC: matrix of significance tests. #columns 1 and 2: Identification numbers of #dose or scenario groups #column 3: p-value for the bilateral test #column 4: alpha_i value to be compared with p-value CCC<-CC[,1:4][CC[,5]==1] dim(CCC)<-c(L,4) cat ("\n") cat ('** Application of Holm-Bonferroni p-value corrections **',"\n") cat ('--------------------------------------------------------',"\n") if (L==0) { cat ('** Non significant differences between any pair of variances **',"\n")} if (L > 0) { cat ('** Pairs of variances that are different **',"\n") cat ('Doses Doses p-value H-B correction',"\n") cat ('----- ----- ------- --------------',"\n") for (i in 1:L) { cat(format(keys[CCC[i,1]],width=12),format(keys[CCC[i,2]],width=12) format(CCC[i,3],width=8,digits=5)format(CCC[i,4],width=9,digits=5),"\n")} cat ('Significant because p-value < Holm-Bonferroni correction',"\n") } cat ('--------------------------------------------------------',"\n") cat ('********************************************************',"\n") # End of the program # Notes: # -----# When running attach(data), the message # The following object(s) are masked from data # (position 3): # Key LAG # should be ignored # For data in which the decimal is marked with a comma instead of a period# use the following sentence without the # symbol # data<-read.table("clipboard",dec=",",header=T#) # Data can be read from CSV files exported from Excel # For data in which the decimal is marked with a # period, use the following # sentence without the # symbol # data<-read.csv2("complete-file-name",header=T#) # For data in which the decimal is marked with a comma, use the following # sentence without the # symbol # data<- read.csv("complete-file-name",header=T) # Example of complete-file-name: # c:/data/VT2kgy.csv # To avoid the following error # Error en win.graph() : too many devices open # close graphing devices when many are open # To avoid the following error # Error en var(LAG[Key == keys[1]]) : 'x' is empty # ensure that the names in the column Key of the # Excel file are # the same as the names given in the sentence # if (groups_number ...) keys <- c('A',...)

