Journal of High Energy Physics, Gravitation and Cosmology
Vol.03 No.01(2017), Article ID:73779,32 pages
10.4236/jhepgc.2017.31014
Does Entropy Manufacture Impacts DM Density Profiles and How Well Does the Scientific Community Understand If or Not Gravity Is always Either a Classical and/or Quantum Phenomenon at Its Genesis over 13.7 Billion Years Ago?
Andrew Walcott Beckwith
Physics Department, College of Physics, Chongqing University Huxi Campus, Chongqing, China

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: January 18, 2016; Accepted: January 21, 2017; Published: January 24, 2017
ABSTRACT
In the 12th Marcel Grossmann Meeting, July 9th, 2009, the author raised the issue of whether early graviton production could affect non-Gaussian contributions to DM density profiles. Specifically, does a first-order phase transition, in the formation of GW also lead to variation in density fluctuations of space plasma production? and curvature perturbations? We submit that the answer to this question will lead to quantifying fluctuations in space time which affect the stability and formation of DM halos and DM density profiles. Furthermore, we look at whether or not there is a relationship between DM and DE, and gravitons. This is suggested by a modification of Randal Sundrum brane world models, which may be used to admit a very small four-dimensional standard space time non-zero graviton mass. Non zero graviton mass in 4 dimensional space time, as well as modification of existing KK graviton theories will lead to a speed-up of cosmological expansion when the red shift was approximately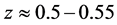 , i.e., about a billion years ago. Finally, the issue of if gravity is a quantum phenomenon will be brought up in the context of understanding if or not squeezing of coherent states is mandatory at the onset of inflation.
, i.e., about a billion years ago. Finally, the issue of if gravity is a quantum phenomenon will be brought up in the context of understanding if or not squeezing of coherent states is mandatory at the onset of inflation.
Keywords:
KK Graviton Theories, Non-Zero Graviton Mass, Non-Gaussian Contributions to DM Density Profiles

1. Introduction
We wish to study how relic gravitational waves relate to relic gravitons [1] , in order to answer some basic questions as to the likelihood of detection of GW, using appropriate instrumentation. To achieve this, we will examine some of the startling similarities and differences between GW equation dynamics and Kaluza-Klein (KK) gravitons [2] . This issue of apparently combined sources of planar wave generation of gravitational waves is a precursor to what would happen if squeezed states occurred in the onset of the big bang. i.e. what would happen with multiple super position of different coherent states? Part of what happens is that squeezed states in the beginning of inflation may be similar to multiple vacuum states contributing to different coherent states. Thereby introducing, at the beginning of inflation non Gaussian contributions to the initial relic gravitational wave forms. The sticking point is that, GWs are composed of coherent states of many gravitons [3] , and coherent state of gravitons requires minimization of uncertainty and as in the simple harmonic oscillator (SHO), small deviations at best from semi-classical approximations. In the case of relic conditions, at the onset of inflation, there are many contributing vacuum states [4] , which would make minimization of uncertainty highly problematic. However, the author suggests (for reasons to be presented in this paper) that gravitons from non-relic conditions may conceivably be measurable, although with difficulty. Recently [5] a PRD paper (Dr. Li et al., 2009) suggests a suitable GW measurement protocol, which may identify relic GW and show whether or not the conditions for graviton measurement are obtainable from astrophysical sources., provided an adequate detector is used. Li’s PRD article [5] assumes a detector which measures the influx of gravitons from these astrophysical sources directly. The reproduced Table 1 presents a generally accepted range of GW frequencies.
Table 1. Magnitude, sources, and top frequency values for HFGW (from Li et al. 2008) [5] .
This reproduced PRD table [5] is important since it suggests that relic GW, if properly measured, may be the first ones to await experimental verification. The PRD authors suggest that focusing on relic GW would be the most likely method of detecting gravitational waves, using the detector design specified in the paper.
2. Review of Simple Models as to Gravitons as Either Due to Strings/Something Else
The following is a review of some of the material .Beckwith presented at Rencontres De Blois [6] , in June, 2009. The summary of concepts will reflect upon interpretation of either the classical and/or quantum foundations of gravitons/ GW. How Equation (0.5) can be used to formulate appropriate operations.
A. Two alternative routes to generation of entropy
We wish to present two alternative routes to generation of entropy. The first, is a counting algorithm, as an adaptation of Y.J. Ng’s infinite quantum (modified Boltz- mann’s) statistics [7] , whereas the second is referencing A. Glinka’s research presentation on “graviton gas [8] ” as a way of understanding a different perspective as to how to get a partition function for gravitons which is congruent to the Wheeler De Witt equation. Here are a few questions which are posed for the reader to think about.
1. Is each “particle count unit” as brought up by Ng, equivalent to a brane-antibrane unit in brane treatments of entropy?
2. Is the change of entropy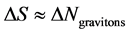 ?
?
3. Is this graviton production scheme comparable to Glinka’s quantum gas, from the Wheeler De Witt equation?
We wish to understand the linkage between dark matter and gravitons. To consider just that, we look at the “size” of the nucleation space, V. V for nucleation is HUGE. Graviton space V for nucleation is tiny, well inside inflation/therefore, the log factor drops OUT of entropy S if V chosen properly for both Equation (1) and Equation (2). Ng’s [7] result begins with a modification of the entropy/partition function Ng used the following approximation of temperature and its variation with respect to a spatial parameter, starting with temperature 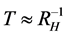 (
( can be thought of as a representation of the region of space where we take statistics of the particles in question). Furthermore, assume that the volume of space to be analyzed is of the form
can be thought of as a representation of the region of space where we take statistics of the particles in question). Furthermore, assume that the volume of space to be analyzed is of the form  and look at a preliminary numerical factor we shall call
and look at a preliminary numerical factor we shall call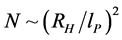 , where the denominator is Planck’s length (on the order of
, where the denominator is Planck’s length (on the order of 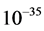 centimeters). We also specify a “wavelength” parameter
centimeters). We also specify a “wavelength” parameter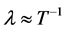 . So the value of
. So the value of 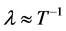 and of
and of 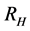 are approximately the same order of magnitude. Now this is how Jack Ng changes conventional statistics: he outlines how to get
are approximately the same order of magnitude. Now this is how Jack Ng changes conventional statistics: he outlines how to get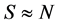 , which with additional arguments we refine to be
, which with additional arguments we refine to be  (where
(where 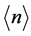 is graviton density). Begin with a partition function
is graviton density). Begin with a partition function
 (1)
(1)
This, according to Ng, [7] leads to entropy of the limiting value of, if 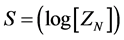
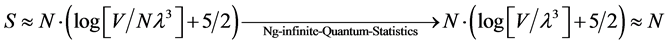 (2)
(2)
But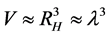 , so unless N in Equation (0.2) above is about 1, S (entropy) would be < 0, which is a contradiction. Now this is where Jack Ng introduces removing the N! term in Equation (1) above, i.e., inside the Log expression we remove the expression of N in Equation (2) above. The modification of Ng’s entropy expression [9] is in the region of space time for which the general temperature dependent entropy Kolb and Turner expression breaks down. In particular, the evaluation of entropy we do via the modified Ng argument above is in regions of space time where
, so unless N in Equation (0.2) above is about 1, S (entropy) would be < 0, which is a contradiction. Now this is where Jack Ng introduces removing the N! term in Equation (1) above, i.e., inside the Log expression we remove the expression of N in Equation (2) above. The modification of Ng’s entropy expression [9] is in the region of space time for which the general temperature dependent entropy Kolb and Turner expression breaks down. In particular, the evaluation of entropy we do via the modified Ng argument above is in regions of space time where 







where

tion (with 

Such a linkage would open up the possibility that the density of primordial gravitational waves could be examined, and linked to modeling gravity as an effective theory. The details of linking what is done with Equation (2) and bridging it to Equation (3) await additional theoretical development, and are probably conceptually understandable if the following is used to link the two regimes. i.e. we can use the number of space time operations used to create Equation (2), via Seth Lloyds [10]

Essentially, what will be done is to use Equation (5) to show linkage between a largely thermally based production of entropy, as implied by Equation (3) and a particle counting algorithm, as given by Equation (2). This due to the problems inherent in making connections between a particle count generation of entropy, and thermal contributions. i.e. two different processes are involved.
C. Introduction. Connection between gravitons and GWs
The first topic to raise is whether or not there is a way to make a connection between gravitons and GWs. In perturbative string theory, a graviton is a closed string in a very particular low-energy vibrational state. And in string theory, a graviton can be connected to a gravitational wave by linking the graviton particle to the curvature of the space-time continuum and calculating the gravitational force exerted. Unfortunately, for string theory, the only way to link gravitons to GWs is by obtaining the coherent state of many gravitons, i.e., looking at Gaussian states with minimum uncertainty, which would be stationary However, as Grishchuck showed, as reported by Allen, Flanagan, and Papa [11] (1999) relic GW generation is Gaussian, but NOT stationary,... Now can a standard planar approximation optimally work for detecting GWs? Probably not, based on Ming-Lei Tong and Yang Zhang [12] (2007), using GW spectra and numerical simulations, which gave a null result for detector (circular waveguides). This result has already been established by Ingley and Criuse (2001) [13] . So, let us see how the inputs gravitational waves OF WHAT? to the circular wave guide via numerical representation of planar waves for GW/ Gravitons MEANING? was initiated.
To do this, we need to consider the behavior of relic GW, as suggested by Tong and Zhang [12] (2007): 


This has the very simple solution, with a mean average for the approximate square of

where the spectrum 








This is where one can write
where 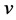




via the time of equality between dark energy and matter density, with 




Figure 1. i.e. how we obtain from the “bottom up” development of galactic super structure [44] .
kilometers, which would make modified gravitational measurements a near impossibility. i.e. one of the challenges would be to see if or not experimental protocol exists that would allow tests of

Obviously, the issue of whether or not a graviton has a mass will impact how realistic the approximations given really are, as well as be important to the issue which Leszek M. Sokolowski, Andrzej Staruszkiewicz [16] (2006) raised: “The graviton must have features different from those of the photon and these cannot be predicted from classical general relativity.” This will impact strongly upon how to analyze the relationship between wavelength 

D. Linkage of DM to gravitons and gravitational waves?
Let us state that the object of early universe GW astronomy would be to begin with confirmation of whether or not relic GW were obtainable , and then from there to ascertain is there is linkage which can be made to DM production... Durrer, Massimiliano Rinaldi (2009) [18] , state that there would be probably negligible for this case (practically nonexistent) graviton production in cosmological eras after the big bang.. In fact, they state that they investigate the creation of massless particles in a Universe which transits from a radiation-dominated era to any other (via an) expansion law. “We calculate in detail the generation of gravitons during the transition to a matter dominated era. We show that the resulting gravitons generated in the standard radiation/matter transition are negligible” This indicated to the author, Beckwith, that it is appropriate to look at the onset of relic GW/Graviton production. Note also that Ruth Durrer, Massimiliano Rinaldi [18] state furthermore in their conclusions: “a graviton spectrum present at the beginning of the radiation era can become significantly amplified and modified by intermediate, non standard evolution of the universe”. This is in part what will be suggested. A non standard evolution protocol which delivers One of the cruder ways of delineating the evolution of GW is the super adiabatic approximation, done for when 


Which to first order when 

This will be contrasted with a very similar evolution equation for gravitons, of the form (i.e. KK gravitons in higher dimensions)

One of the most frequently appealed to models of linkage between gravitons, and DM is the so called KK graviton, i.e. as a DM candidate. KK gravitons. Note that usual Randal Sundrum brane theory has a production rate [20] of

as the number of Kaluza Klein gravitons per unit time per unit volume Note that this production rate is for a formula assuming mass for which


where R is the assumed higher dimension “size” and, d is the number of dimensions above 4, and typically we obtain

If KK gravitons have the same wavelength as DM, this will support Jack Ng’s [7] treatment of DM. All that needs to put this on firmer ground will be to make a de facto linkage of KK Gravitons, as a DM candidate, and more traditional treatments of gravitons, which would assume a steady drop in temperature from






As well as being related to an overall wave functional which can be derived from a line element

With 
equation for the KK gravitons is very smilar to work done by Baumann, Daniel, Ichiki, Kiyotomo, Steinhardt, Paul J. Takahashi, Keitaro [23] (2007) with similar assumptions, with the result that KK gravitons are a linear combination of Bessel functions. Note that one has for gravitions [20] [21] .

Ruth Gregory, Valery A. Rubakov and Sergei M. Sibiryakov [24] (2000) make the additional claim that for large z (the higher dimensions get significant) that there are marked oscillatory behaviors, i.e. Rapid oscillations as one goes into the space for branes for massive graviton expansion [21] , [24] .

This is similar to what Baumann, Daniel, Ichiki, Kiyotomo, Steinhardt, Paul J. Takahashi , Keitaro [23] (2007) for GW, in a relic setting, with the one difference being that the representation for a graviton is in the z ( additional dimension) space, as opposed to what Bauman et al. did for their evolution of GW, with an emphasis upon generation in
overall GR space time. Furthermore, the equation given in
for massive graviton evolution as KK gravitons along dS branes is similar to evolution of GW in more standard cosmology that the author, Beckwith, thinks that the main challenge in clarifying this picture will be in defining the relationship of dS geometry, in overall Randall Sundrum brane world to that of standard 4 space. We need though, now to look at whether or not higher dimensions are even relevant to GR itself.
3. Now the Main Topic: How Would DM Be Influenced by Gravitons, in 4 Dimensions
We will also discuss the inter relationship of structure of DM, with challenges to Gaussianity. The formula as given by [25] , [26]

will be gone into the variation, so alluded to which we will link to a statement about the relative contribution of Gaussianity, via looking at the gravitational potential [26] [27]

Here the expression 





It is note worthy to note that the question of DM/ KK gravitons, and also the mass of the graviton not only has relevance to whether or not, higher dimensions are necessary/ advisable in space time models , but also may be relevant to if massive gravitons may solve/partly fulfill the DE puzzle. To whit, KK gravitons would have a combined sum of Bessel equations as a wave functional representation. In fact V. A. Rubasov [20] [21] writes that KK graviton representation as, after using the following normalization
where 

This allegedly is for KK gravitons having an order of TeV magnitude mass 


mass, before the KK graviton, as a “massive” graviton moves with velocity 
the RS dS brane. If so, and if 
then one may relate the mass of the KK gravition, moving at high speed, with the initial rest mass of the graviton, which in four space in a rest mass configuration would have a mass many times lower in value, i.e. of at least




In the case of working with a simpler version of the Friedman equation with no graviton mass, but with pressure and density factored in, we can obtain [29] [30] [31]

This will lead to a very simple de celebration parameter value of [29] [30] [31]

The article will see what happens to insure whether or not the sign of Equation (25) and Equation (26) and Equation (26) goes from positive to negative. Needless to say, if one has a graviton mass

And [29] [30] [31]

For the matter dominated era, it is important to note that the R.H.S. of Equation (28) is zero. This leads to Equation (26) having increasingly positive acceleration values as would be definitely be given for masses of 



equation. i.e. when using ultra low graviton mass, where 
and 


As can be related to, if we wish to look at string theory versions of the FRW equation, in Friedman-Roberson-Walker metric space, we can do the following decomposition, with different limiting values of the mass, and other expressions, e.g. as a function of an existing cosmological constant.

As well as

Not only this, if looking at the brane theory Friedman equations as presented by/for Randall Sundrum theory, it would be prudent working with [32]

For the purpose of Randal Sundrum brane worlds, Equation (32) is what will be differentiated with respect to
a derivable equation which will be for a RS brane world version of
different versions of what q should be will be offered as far as what the time dependence of terms in 1.10 actually is. Note that Roy Maartens has written as of 2004 that KK modes [32] (graviton) satisfy a 4 Dimensional Klein-Gordon equation, with an ef-
fective 4 dim mass, 

“dimensional value” of higher dimensions. The value 


and

If one is adding, instead the small mass of [34]

with 

This is, using the language V.A. Rubakov [20] [21] put up equivalent to writing, using Equation (28)

i.e. how to inteprept the quantity 

A. Not everyone buys dark energy. i.e. Controversies of DM/DE applications to cosmology. How HFGW may help resolve them
The following is meant as a travelogue as to current problems in cosmology which will require significant revision of our models. Exhibit A as to what to consider is the cosmic void hypothesis’. See Timothy Clifton, Pedro G. Ferreira and Kate Land [36] . i.e. Clifton raises the following question-can HFGW and detectors permit cosmologist to get to the bottom of this? “Solving Einstein’s equations for an averaged matter distribution is NOT the same as solving for the real matter distribution and then averaging the resultant geometry” (“We average, then solve when in effect we should solve, then average”).
Next, let us look at a recently emerging conundrum of DM feeding into the structure of new galaxies and their far earlier than expected development, i.e. 5 billion years after the big bang. Galaxy formation issues… Hierarchical Galaxy Formation theory at a glance usually proceeds as follows. i.e. what happens when the following diagram of simple addition of new structure no longer holds ? This is very significant, since when the significant formation of galaxies occurs, as of about 


Several scenarios which will be investigated. First of all, note the formula of variation of DM density which exists has, among other things a Hubble parameter H, and also the 2nd derivative of the gravitational potential



and

then the contribution of large




When using the formula, 







Then

Alternately, if the brane theory model of a gravitational potential were used, with KK graviton modes, then

Now for some sort of bounds as to what may be acceptable bounds in error, based upon CMB data

Depending upon which model is used for describing 



Non-linear dynamics at recombination will lead to, for CMBR a treatment similar to what was given by Jean-Luc Lehners, Paul J. Steinhardt, (2009) [39] , i.e., if 


Also, White and Hu [41] (1996), also have a convenient way to link the gravitational potential 


A simple way to understand what is said by Equation (46) is to consider if or not it is linkable to the Sach-Wolfe effect. Here, the Sachs-Wolfe effect (ISW) occurs when the Universe is dominated in its density by something other than matter. If the Universe is dominated by matter, then large-scale gravitational potential wells and hills do not evolve significantly. If the Universe is dominated by radiation, or by dark energy, though, those potentials do evolve, subtly changing the energy of photons passing through them. If there is a major difference in the initial and final ratios 
good approximation,
are valid, then one has, say

Equation (47) has its counterpart in what Daniel Babich, Paolo Creminelli, Matias Zaldarriaga [42] (2004) about the influence of curvature “perturbations” with some of them being linear, and the others showing a slight perturbative effect. i.e. look at

Here, 


where we use


What is actually observed, contradicts this halo emerging history “tree”, i.e. Although this “story” for DM seems to be well established. i.e. Just ONE little problem: DM appears to be fattening up young galaxies, allowing for far-earlier-than-expected creation of early galaxies. “A clutch of massive galaxies that seem to be almost fully-formed just 5 billion years after the big bang challenge models that suggest galaxies can only form slowly. Tendrils of dark matter that fed the young galaxies on gas could be to blame (NASA/CXC/ESO/P Rosati et al.)” [45] leading to [46] .
Needless, to say though, an analysis of the influence of DM on structure formation would have to take into consideration the datum presented by [47] as reporting upon the data analysis of G. Hinsaw [48] and others as to the relative super abundance of DM in early universe conditions. i.e. considering the following. The relative imprecision of graviton measurement, can be given as follows. This is a measurement in particle physics, and if the KK graviton is linkable to DM, it means that we will have to have very good ways to test for production rates, as will be argued later. The following below is a typical representation of the KK tower model for gravitons, with the zeroth KK mode being approximately the 4 dimensional graviton. From scattering data, the relative mass contributions show up, as follows for KK gravitons, as modeled below. These representation are for leading up to investigating if or not one needs KK gravitons, as either a semi classical, or a brane theory/string theory construct, as a was of determining if either.
1) Gravitons have mass, i.e. 

2) DE style expansion at 
3) DM may be connected with KK variants of higher dimensional generalizations of 
4) The issue of if or not gravitons/entropy/constituent DM may be linked to instanton physics models of gravitons Understanding the KK gravitons as a DM candidate may permit us to understand how DM and DE are inter related. See as given below. The discussion of such will involve coherent state of gravitons as contributors to GW. This is the message of Figure 2 below.
Figure 2. From G. Hingsaw presentation, in COMO, Italy, July 2009 at the ISAPP [49] .
How DM, and other constituent parts of the early 380 thousand year old universe evolved to have connections with KK gravitons is connected closely with the following
B. Issues about Coherent state of Gravitons (linking gravitons with GW)
In the quantum theory of light (quantum electrodynamics) and other bosonic quantum field theories , coherent states were introduced by the work of Roy J. Glauber in 1963 [50] Now, it is well appreciated that Gravitons are NOT similar to light. So what is appropriate for presenting gravitons as coherent states? Coherent states, to first approximation are retrievable as minimum uncertainty states. If one takes string theory as a reference, the minimum value of uncertainty becomes part of a minimum uncertainty which can be written as given by Maggiorie, [51] and Venziano [52] , where



To put it mildly, if we are looking at a solution to minimize graviton position uncertainty, we will likely be out of luck if string theory is the only tool we have for early universe conditions. Mainly, the momentum will not be small, and uncertainty in momentum will not be small either. Either way, most likely, 


And that is the problem, with regards to string theory, what is an appropriate vacuum expectation value for treating a template of how to nucleate gravitons into a coherent state with respect to relic conditions. Ford, in 1994 [55] , wrote a squeezed state operation S () via



Here, the value 










C. Can any detector measure
Not now. Current limits would be, for 





However, what one sees in string theory, is a situation where a vacuum state as a template for graviton nucleation is built out of an initial vacuum state,



where combining the 

The right hand side of Equation (54) given above becomes a highly non classical operator, i.e. in the limit that the super position of states 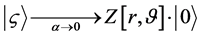











If 






Then the Lagrangian for deriving Equation (56) is (and leads to a Hamiltonian which can be also derived from the Wheeler De Witt equation), with 


then there are two possible solutions to the S.E. Grushchuk created in 1989 [57] , one a non squeezed state, and another a squeezed state. So in general we work with

The non squeezed state has a parameter 





Taking Grishchuck’s formalism literally, a state for a graviton/GW is not affected by squeezing when we are looking at an initial frequency, so that 



cuum state being initially formed right after the point of nucleation, with 











D. Necessary and sufficient conditions for String/Brane theory graviton coherent states?
A curved spacetime is a coherent background of gravitons, and therefore in string theory is a coherent state Joseph Gerard Polchinski [3] starting with the typical small deviation from flat space times as can be written up by



becomes [3]

Polochinski [3] writes that the term of order 





E. Does LQG give us more direct arguments as to coherent states, squeezed states, and the breakdown of classical behavior at the onset of inflation?
Carlo Rovelli [63] , in 2006, in a PRL article states that a vertex amplitude that contributes to a coherent graviton state is the exponential of the Regge action: the other terms, that have raised doubts on the physical viability of the model, are suppressed by the phase of the vacuum state, and Rovelli writes a coherent vacuum state as given by a Gaussian peaked on parts of the boundary 

Rovelli states that “bad” contributions to the behavior of Equation (63) are cancelled out by an appropriate (Gaussian?) vacuum wave functional which has “appropriately” chosen contributions from the boundary 




Furthermore, Bojowald [68] (2008) specified a criteria as to how to use an updated version of 



and 


when the Friedman equation is quantized, with an initial internal time given by


for his Equation (26), which is incidently when links to classical behavior break down, and when the bounce from a universe contracting goes to an expanding present universe. Bojowald [68] also writes that if one is looking at an isotropic universe, that as the large matter “H” increases, that in certain cases, one observes more classical behavior, and a reduction in the strength of a quantum bounce.. Bojowalds [68] states that “Especially the role of squeezed states is highlighted. The presence of a bounce is proven for uncorrelated states, but as squeezing is a dynamical property and may change in time” The upshot is that although it is likely in a quantum bounce state that the states should be squeezed, it is not a pre requisite for the states to always start off as being squeezed states. .So a physics researcher can, look at if an embedding of the present universe in a higher dimensional structure which could have lead to a worm hole from a prior universe to our present for re introduction of inflationary growth.
F. Other models. Do worm hole bridges between different universes allow for initial un squeezed states? Wheeler De Witt solution with pseudo time component added in.
This discussion is to present a not so well known but useful derivation of how instant on structure from a prior universe may be transferred from a prior to the present universe.
1. The solution as taken from L. Crowell’s (2005) [69] book, and re produced here, as referenced by Beckwith (2008, 2009) has many similarities with the WKB method. i.e. it is semi CLASSICAL.
2. left unsaid is what embedding structure is assumed
3. A final exercise for the reader. Would a WKB style solution as far as transfer of “material” from a prior to a present universe constitute procedural injection of non compressed states from a prior to a present universe? Also if uncompressed, coherent states are possible, how long would they last in introduction to a new universe?
This is the Wheeler-De-Witt equation with pseudo time component added. From Crowell [69]

This has when we do it


In order to do this, we can write out the following for the solutions to Equation (67) above [69] .

And

This is where 



is stable under evolution of space-time leading up to inflation. To model this, we use results from Crowell (2005) [69] on quantum fluctuations in space-time, which gives a model from a pseudo time component version of the Wheeler-De-Witt equation, with use of the Reinssner-Nordstrom metric to help us obtain a solution that passes through a thin shell separating two space-times. The radius of the shell 


This has:

This assumes that the cosmological vacuum energy parameter has a temperature dependence as outlined by Park [70] (2003), leading to

as a wave functional solution to a Wheeler-De-Witt equation bridging two space-times, similar to two space-times with “instantaneous” transfer of thermal heat, as given by Crowell (2005) [69]

This has 


Now in the case of what can be done with the worm hole used by Crowell, with, if



gy value as given of the form



G. Creating an analysis of how graviton mass, assuming branes, can influence expansion of the universe
Following development of *(1.13) as mentioned above, with inputs from Friedman eqns. To do this,, the following normalizations will be used, i.e.

where




Furthermore, if we are using density according to whether or not 4 dimensional graviton mass is used, then

So, then one can look at 

Here, use,

and
If

Now, if, to first order, 



Also, then, set the curvature equal to zero. i.e.


Then


Pick, here,

after




For what it is worth, the above can have the shift to red shift put in by the following substitution. i.e. use













So, for


Easy to see though, that to first order, 






4. Conclusions: Unanswered Questions, and What This Suggests for Future Research Endeavors
As far back as 1982 [74] , Linde, when analyzing a potential of the form

This is when the “mass” has the form, (here M is the bare mass term of the field 

Specified non linearity of 

The question raised repeatedly in whether or not i) if higher dimensions are necessary, and whether or not ii) mass gravitons are playing a role as far as the introduction of DE speed up of cosmological expansion may lead to an improvement over what was specified for density fluctuations and structure formation (the galaxy hierarchy problem) of density fluctuations given as

Equation (105) is for four space, a defining moment as to what sort of model would lead to density fluctuations. It totally fails as to give useful information as to the galaxy hierarchy problem as given in Figure 1, above. Secondly, to what degree is the relative speed up of the q(z) function is impacted by various inter plays between, say a MODIFIED version of, say a KK DM model, using a MODIFIED mass hierarchy to get suitable DM masses of the order of 100 GeV or more. Giving a suitable definition as to q(z) as well as the inter play between DM values, 4 Dim Graviton mass issues, and/or what really contributes to the speed up of the universe will in the end dramatically improve the very crude estimate given by Equation (105) above which says next to nothing about how the problems illustrated by the breakdown of the galaxy mass formation/ hierarchy can be fixed. Furthermore is considering the spectral index problem, where the spectral index is [74]

Usual experimental values of density fluctuations experimentally are




ferent models of how density fluctuation may have to be devised. A popular model of density fluctuations with regards to the horizon is

where






and 


The above equation gives inter relationships between the time evolution of a pop up inflaton field




To first order, variations of 




The follow ups to the conclusion are THAT WE stress that the achievement of conditions allowing us to do research ON THE FUNDATIONS OF A WORKING gravitational wave astronomy research protocol, will be important for discriminating among general relativity and other gravity theories, as it has been shown in [75] .
i.e. we need to understand what gravity is. That is basic.
Furthermore, the foundational issues brought up by the LIGO discovery should be confirmed and expanded upon as given in [76] and [77] .
Acknowledgements
This work is supported in part by National Nature Science Foundation of China grant No. 11375279.
Cite this paper
Beckwith, A.W. (2017) Does Entropy Manufacture Impacts DM Density Profiles and How Well Does the Scientific Community Understand If or Not Gravity Is always Either a Classical and/or Quantum Phenomenon at Its Genesis over 13.7 Billion Years Ago? Journal of High Energy Physics, Gravitation and Cos- mology, 3, 106-137. http://dx.doi.org/10.4236/jhepgc.2017.31014
References
- 1. Penrose, R. (2007) The Road to Reality: A Complete Guide to the Laws of the Universe. Vintage Books, New York.
- 2. Wesson, P.S. (1999) Space-Time-Matter, Modern Kaluza-Klein Theory. World Scientific, Singapore.
https://doi.org/10.1142/3889 - 3. Polchinski, J. String Theory Volume 1: An Introduction to the Bosonic String.
http://ebooks.cambridge.org/ebook.jsf?bid=CBO9780511816079 - 4. Haisch, B., Rueda, A. and Dobyns, Y. (2001) Inertial Mass and the Quantum Vacuum Fields. Annalen der Physik, 10, 393-414. arXiv:gr-qc/0009036.
- 5. Tong, M.-L., Zhang, Y. and Li, F.-Y. (2008) Using Polarized Maser to Detect High-Frequency Relic Gravitational Waves. Physical Review D, 78, Article ID: 024041.
http://arxiv.org/abs/0807.0885
https://doi.org/10.1103/PhysRevD.78.024041 - 6. Beckwith, A.W. (2009) Entropy Growth in the Early Universe and Confirmation of Initial big Bang Conditions (Wheeler De Witt Eqn. Results vs. String Theory?).
http://vixra.org/abs/0908.0109 - 7. Ng, Y. (2008) Spacetime Foam: From Entropy and Holography to Infinite Statistics and Nonlocality. Entropy, 10, 441-461.
https://doi.org/10.3390/e10040441 - 8. Glinka, L. (2007) Quantum Information from Graviton-Matter Gas. Sigma, 3, 087, 13 p.
- 9. Kolb, E. and Turner, S. (1994) The Early Universe. Westview Press, Chicago.
- 10. Lloyd, S. (2002) Computational Capacity of the Universe. Physical Review Letters, 88, Article ID: 237901.
https://doi.org/10.1103/PhysRevLett.88.237901 - 11. Allen, B., Flanagan, E. and Papa, M.A. (2000) Is the Squeezing of Relic Gravitational Waves Produced by Inflation Detectable? Physical Review D, 61, Article ID: 024024.
http://arxiv.org/PS_cache/gr-qc/pdf/9906/9906054v2.pdf
https://doi.org/10.1103/PhysRevD.61.024024 - 12. Tong, M.-L. and Zhang, Y. (2007) Detecting Very-High-Frequency Relic Gravitational Waves by Electromagnetic Wave Polarizations in a Waveguide. Chinese Journal of Astronomy and Astrophysics, 8 (2008), 314-328.
http://arxiv.org/abs/0711.4909
https://doi.org/10.1088/1009-9271/8/3/08 - 13. Ingley, R.M.J. and Cruise, A.M. (2001) An Electromagnetic Detector for High Frequency Gravitational Waves. 4th Edoardo Amaldi Conference on Gravitational Waves, Perth, Australia, July 2001.
- 14. Linder, E. (2003) Exploring the Expansion History of the Universe. Physical Review Letters, 90, Article ID: 091301.
https://doi.org/10.1103/PhysRevLett.90.091301 - 15. Will, C. (1997) Bounding the Mass of the Graviton Using Gravitional-Wave Observations of Inspiralling Compact Binaries.
http://arxiv.org/abs/gr-qc/9709011 - 16. Sokolowski, L.M. and Staruszkiewicz, A. (2006) On the issue of Gravitons. Classical and Quantum Gravity, 23, 5907-5918.
http://arxiv.org/abs/gr-qc/0606111
https://doi.org/10.1088/0264-9381/23/20/012 - 17. Janssen, B. and Lozano, Y. (2003) A Microscopical Description of Giant Gravitons. Nuclear Physics B, 658, 281-299.
https://arxiv.org/abs/hep-th/0207199
https://doi.org/10.1016/S0550-3213(03)00185-8 - 18. Durrer, R. and Rinaldi, M. (2009) Graviton Production in Non-Inflationary Cosmology. Physical Review D, 79, Article ID: 063507.
http://arxiv.org/abs/0901.0650
https://doi.org/10.1103/PhysRevD.79.063507 - 19. Giovannini, M. (2008) A Primer on the Physics of the Cosmic Microwave Background. World Press Scientific, Singapore.
- 20. Rubakov, V.A. Large and Infinite Extra Dimensions.
http://arxiv.org/pdf/hep-ph/0104152.pdf - 21. Rubakov V. (2002) Classical Theory of Gauge Fields. Princeton University Press, Princeton, Translated by Stephen S. Wilson, 456 p.
- 22. Rubakov, V.A. (2009) Baikal Summer School on Physics of Elementary Particles and Astrophysics; Talk Given in This Conference, i.e. Notes.
- 23. Baumann, D., Ichiki, K., Steinhardt, P.J. Takahashi, K. Gravitational Wave Spectrum Induced by Primordial Scalar Perturbations. arXiv:hep-th/0703290
- 24. Gregory, R. Rubakov, V.A. and Sibiryakov, S.M. (2000) Brane Worlds: The Gravity of Escaping Matter. Classical and Quantum Gravity, 17, 4437-4450.
https://arxiv.org/abs/hep-th/0003109
https://doi.org/10.1088/0264-9381/17/21/306 - 25. Fedeli, C., Moscardini, L. and Matarrese, S. (2009) The Clustering of Galaxy Clusters in Cosmological Models with Non-Gaussian Initial Conditions: Predictions for Future Surveys. Monthly Notices of the Royal Astronomical Society, 397, 1125-1137.
http://arxiv.org/abs/0904.3248
https://archive.org/stream/arxiv-0904.3248/0904.3248_djvu.txt
https://doi.org/10.1111/j.1365-2966.2009.15042.x - 26. Matarrese, S. (2009) Lecture, 10 July 2009. International School of Astroparticle Physics, Como.
- 27. Beckwith, A. (2010) Entropy, Neutrino Physics, and the Lithium Problem: Why Are There Stars with Essentially No Lithium Due to Serious Lithium Deficiency in Certain Spatial Regions in the Early Universe? Progress in Particle and Nuclear Physics, 64, 426-428.
https://doi.org/10.1016/j.ppnp.2009.12.066 - 28. Dubovsky, S., Flauger, R., Starobinsky, A. and Thackev, I. (2009) Signatures of a Graviton Mass in the Cosmic Microwave Background. Physical Review D, 81, Article ID: 023523, 2010.
https://arxiv.org/abs/0907.1658
https://doi.org/10.1103/PhysRevD.81.023523 - 29. Alves, M.E.S., Miranda, O.D. and de Araujo, J.C.N. (2009) Can Massive Gravitons Be an Alternative to Dark Energy? arXiv:0907.5190
- 30. Jones, M.H. and Lambourne, R.J. (2004) An Introduction to Galaxies and Cosmology. Cambridge University Press, Cambridge, UK, 244.
- 31. Bolotin, Yu.L., Cherkaskiy, V.A., Lemets O.A., Yerokhin, D.A. and Zazunov, L.G. Cosmology in Terms of the Deceleration Parameter. Part I.
http://arxiv.org/pdf/1502.00811.pdf - 32. Maartens, R. (2004) Brane-World Gravity.
http://www.livingreviews.org/lrr-2004-7 - 33. Grössing, G. From Classical Hamiltonian Flow to Quantum Theory: Derivation of the Schrödinger Equation.
https://arxiv.org/ftp/quant-ph/papers/0311/0311109.pdf - 34. Beckwith, A. Identifying a Kaluza Klein Treatment of a Graviton Permitting a Deceleration Parameter Q(Z) As An Alternative to Standard DE.
http://journalofcosmology.com/BeckwithGraviton.pdf - 35. Peskins, M. and Schroeder, D. (1995) An Introduction to Quantum Field Theory. Westview Press, Palo Alto.
- 36. Clifton, T., Ferreira, P.G. and Land, K. (2008) Living in a Void: Testing the Copernican Principle with Distant Supernovae. Physical Review Letters, 101, Article ID: 131302.
https://arxiv.org/abs/0807.1443
https://doi.org/10.1103/PhysRevLett.101.131302 - 37. Verde, L. Non Gaussianity versus Non Linearity of Cosmological Perturbations. Proc. of the 15th Florida workshop in Nonlinear Astronomy and Physics. Annals of The New York Academy of Sciences as well as.
http://arxiv.org/abs/astro-ph/0004341 - 38. Chingabam, P. and Park, C. Statistical Nature of Non Gaussianity from Cubic Order Primoridal Perturbations: CMB Map Simulations and Genus Statistics.
http://arxiv.org/PS_cache/arxiv/pdf/0908/0908.1696v1.pdf - 39. Lehners, J.-L. and Steinhardt, P.J. (2008) Non-Gaussian Density Fluctuations from Entropically Generated Curvature Perturbations in Ekpyrotic Models. Physical Review D, 77, Article ID: 063533.
http://arxiv.org/abs/0712.3779
https://doi.org/10.1103/PhysRevD.77.063533 - 40. Bardeen, J.M. (1980) Gauge-Invariant Cosmological Perturbations. Physical Review D, 22, 1882-1905.
https://doi.org/10.1103/PhysRevD.22.1882 - 41. White, M. and Hu, W. The Sach-Wolfe Effect.
http://arxiv.org/PS_cache/astro-ph/pdf/9609/9609105v1.pdf - 42. Babich, D., Creminelli, P. and Zaldarriaga M. (2004) The Shape of Non-Gaussianities. CAP, 0408, 009.
http://arxiv.org/abs/astro-ph/0405356 - 43. Lyth, D.H. (2005) Generating Curvature Perturbations at the End of Inflation. JCAP, Article ID: 0511006.
http://arxiv.org/abs/astro-ph/0510443
https://doi.org/10.1088/1475-7516/2005/11/006 - 44. Wechsler, R.H. (2001) Dark Halo Merging and Galaxy Formation. Ph.D. Thesis.
http://risa.stanford.edu/thesis.php - 45. NASA/CXC/ESO/P Rosati et al.
http://chandra.harvard.edu/photo/2004/rdcs1252/ - 46. Rachel Courtland.
https://www.newscientist.com/article/dn16912-overweight-galaxies-force-fed-by-dark-matter-tendrils/ - 47. Björn Helmut Bastian Opitz aus Warburg.
http://www.desy.de/~horns/Opitz_Diss_Druckversion_2014-09-23.pdf - 48. Hinshaw, G., et al. Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Parameter Results.
http://arxiv.org/abs/1212.5226 - 49. Hingsaw G. Presentation, in COMO, Italy, July 2009 at the ISAPP.
- 50. Glauber, R. (1963) Coherent and Incoherent States of the Radiation Field. Physical Review, 131, 2766-2788.
https://doi.org/10.1103/PhysRev.131.2766 - 51. Veneziano, G. (1986) A Stringy Nature Needs Just Two Constants. Europhysics Letters, 2, 199. Proc. of Texas Superstring Workshop (1989).
https://doi.org/10.1209/0295-5075/2/3/006 - 52. Maggiore, M. The Algebraic Structure of the Generalized Uncertainty Principle.
https://arxiv.org/pdf/hep-th/9309034.pdf - 53. Kiefer, C. (2007) Quantum Gravity. International Series of Monographs on Physics, (Hardcover), Oxford Science Publications, Oxford University Press.
- 54. Mohaupt, T. (2003) Introduction to String Theory. Lecture Notes in Physics, 631, 173-251.
https://arxiv.org/abs/hep-th/0207249 - 55. Ford, L.H. Gravitons and Lightcone Fluctuations.
http://arxiv.org/abs/gr-qc/9410047 - 56. Venkataratnam, K.K. and Suresh, P.K. (2008) Density Fluctuations in the Oscillatory Phase of Nonclassical Inflaton in FRW Universe. International Journal of Modern Physics D, 17, 1991-2005.
http://arxiv.org/abs/0712.3129
https://doi.org/10.1142/S0218271808013662 - 57. Grishchuk, L.P. (1998) The Detectability of Relic (Squeezed) Gravitational Waves by Laser Interferometers.
http://arxiv.org/abs/gr-qc/9810055 - 58. Grishchuk, L.P. (1993) Quantum Effects In Cosmology. Classical and Quantum Gravity, 10, 2449-2478.
http://arxiv.org/abs/gr-qc/9302036
https://doi.org/10.1088/0264-9381/10/12/006 - 59. Grishchuk, L.P. (1980) The Problem of Relic Gravitational Radiation. Soviet Physics Uspekhi, 23, 705-706.
- 60. Grishchuk, L. (2008) Discovering Relic Gravitational Waves in Cosmic Microwave Background Radiation.
http://arxiv.org/abs/0707.3319 - 61. Dick, R. (2001) Heterotic String Dark Matter from the Graviton Multiplet. Physics Letters B, 510, 10-16.
https://doi.org/10.1016/S0370-2693(01)00617-7 - 62. Berkenstein (2004).
http://uw.physics.wisc.edu/~strings/group/slides.04.fall/berenstein.pdf - 63. Rovelli, C. (2006) Graviton Propagator from Background-Independent Quantum Gravity. Physical Review Letters, 97, Article ID:151301.
http://arxiv.org/abs/gr-qc/0508124
https://doi.org/10.1103/PhysRevLett.97.151301 - 64. Montl, L. (2007).
http://motls.blogspot.com/2007/08/thiemann-dittrich-discreteness-of-lqg.html - 65. Mielczarek, J. (2009) Tensor Power Spectrum with Holonomy Corrections in Loop Quantum Cosmology. Physical Review D, 79, Article ID: 123520.
http://arxiv.org/abs/0902.2490
https://doi.org/10.1103/PhysRevD.79.123520 - 66. Chiou, D.-W. and Li, L.-F. (2009) Loop Quantum Cosmology With higher Order Holonomy Corrections. Physical Review D, 80, Article ID: 043512.
http://arxiv.org/abs/0907.0640
https://doi.org/10.1103/PhysRevD.80.043512 - 67. Abhay Ashtekar (2006)
http://cgpg.gravity.psu.edu/people/Ashtekar/articles/solvaynet.pdf - 68. Bojowald, M. (2008) Quantum Nature of Cosmological Bounces. General Relativity and Gravitation, 40, 2659-2683.
http://arxiv.org/abs/0801.4001
https://doi.org/10.1007/s10714-008-0645-1 - 69. Crowell, L. (2005) Quantum Fluctuations of Space Time. World Scientific Series in Contemporary Chemical Physics, Vol. 25, World Scientific, PTE, LTD, Singapore.
- 70. Park, D.K., Kim, H. and Tamarayan, S. (2002) Nonvanishing Cosmological Constant of Flat Universe in Brane-World Scenario. Physics Letters B, 535, 5-10.
http://arxiv.org/abs/hep-th/0111081
https://doi.org/10.1016/S0370-2693(02)01729-X - 71. Martín-Moruno, P. and González-Díaz, P.F. (2009) Thermal Radiation from Lorentzian Traversable Wormholes. Physical Review D, 80, Article ID: 024007.
https://arxiv.org/abs/0907.4055 - 72. Cavaglià, M. (1994) Quantum Electromagnetic Wormholes and Geometrical Description of the Electric Charge. Physical Review D, 50, 5087-5092.
http://arxiv.org/abs/gr-qc/9407030
https://doi.org/10.1103/PhysRevD.50.5087 - 73. Garay, L.J. (1991) Quantum State of Wormholes and Path Integral. Physical Review D, 44, 1059-1066.
https://doi.org/10.1103/PhysRevD.44.1059 - 74. Lemoine, M., Martin, J. and Peter, P., Eds. (2008) Linde in Article in Physics 738, Inflationary Cosmology. Springer Verlag, Berlin.
- 75. Corda, C. (2009) Interferometric Detection of Gravitational Waves: The Definitive Test for General Relativity. International Journal of Modern Physics D, 18, 2275-2282.
arXiv:0905.2502 [gr-qc] - 76. Abbott, B.P., et al. (2016) (LIGO Scientific Collaboration and Virgo Collaboration) Observation of Gravitational Waves from a Binary Black Hole Merger. Physical Review Letters, 116, Article ID: 061102.
https://physics.aps.org/featured-article-pdf/10.1103/PhysRevLett.116.061102 - 77. Abbott, B.P., et al. (LIGO Scientific Collaboration and Virgo Collaboration) (2016) GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Physical Review Letters, 116, Article ID: 241103.
https://doi.org/10.1103/PhysRevLett.116.241103

















