Journal of Applied Mathematics and Physics
Vol.06 No.04(2018), Article ID:84023,16 pages
10.4236/jamp.2018.64074
Thin Film Evolution Equation for a Strained Anisotropic Solid Film on a Deformable Isotropic Substrate
Wondimu Tekalign, Agegnehu Atena
Department of Mathematics, Savannah State University, Savannah, GA, USA
Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 23, 2018; Accepted: April 23, 2018; Published: April 26, 2018
ABSTRACT
We consider a continuum model for the evolution of an epitaxially-strained dislocation-free anisotropic thin solid film on isotropic deformable substrate in the absence of vapor deposition. By using a thin film approximation we derived a nonlinear evolution equation. We examined the nonlinear evolution equation and found that there is a critical film thickness below which every film thickness is stable and a critical wave number above which every film thickness is stable.
Keywords:
Thin Films, Evolution Equation, Anisotropy, Hooke’s Law

1. Introduction
Spontaneously formed periodic domain structures of nanoscale islands (quantum dots) in epitaxially strained thin solid films have become a subject of intense theoretical and experimental study. These islands have unique, optical, electronic and magnetic properties which signify their importance in quantum dot applications [1] [2] . These islands are small (a few nanometers) in size and hence difficult to prepare by standard lithographic techniques. One promising way is the formation of islands by a Stranski-Krastanow growth process whereby the planar film undergoes a morphological instability [3] [4] [5] [6] . During heteroepitaxial growth, the instability of surfaces under strain and subsequent island formation is caused by the competition between the surface free energy and the strain energy of the system [7] [8] [9] [10] [11] .
In experimental study of the nonlinear evolution of the stress-driven instability of thick films the formation of deep, cusp-like grooves was observed [12] [13] . In [14] this instability was studied numerically and they showed that the surface instability creates a groove that sharpens as it grows deeper. In [15] a fully nonlinear bifurcation analysis was performed and tracking the branch of steady state solutions numerically they found that the steady state solution branch terminates as the solutions form a cusp singularity.
In a thin film, however, cusp formation is suppressed as the surface approaches the film substrate interface. The different stress fields and the different surface energies of the film and the substrate affect the surface morphology and the film-substrate interface is prevented from being exposed when the wetting criterion is satisfied. Stranski-Krastanow islands will be formed in this case [16] . The steady states of island shapes were studied by many researchers [17] - [22] .
While the understanding of some of the theoretical and modeling issues is well developed, the implementation of the models as large-scale numerical simulations is not yet feasible. The central issue is that the dynamics of the surface morphology is coupled to the elastic strain in the system, so dynamic models require solving the elasticity problems throughout the film and substrate at each time step and are limited by storage limitations for 3-dimensional problem. Simulations involving the full elasticity problem are limited to one or few islands [23] [24] . Only one recent work [25] explored a large number of islands using a large-scale 3-dimensional calculation. This work uses the same elastic constants for both the film and the substrate. In [26] the evolution of a large number of islands was obtained using small slope approximation on a rigid substrate.
In [27] we developed an approximate solution to the elasticity problem which is valid when the film is thin. This elasticity solution is valid for arbitrary elastic constants in the film and substrate. The resulting elasticity solution then removes the necessity for solving the full 3-dimensional elasticity problem numerically, and may provide a means for implementing large-scale simulations. Our work here is to include anisotropic properties of the film to the evolution equation to study the formation of islands. Within this framework, in [28] a non-linear evolution equation with a second-order approximation for the stress field and a nonlinear wetting potential for the interface was considered and it was claimed that the combined effect of nonlinear stress and wetting can terminate the coarsening process and lead to the formation of arrays of equal-sized islands. And, [29] , found that wetting interaction can damp the long-wave perturbations and lead to Turing-type instability, further a weakly nonlinear analysis showed a possibility for spatially periodic arrays of quantum dots which are unstable.
The rest of the paper is organized as follows. In Section 2 we present the full nonlinear model for morphological evolution in thin solid films. In Sections 3 and 4 we describe the thin-film scalings and derive a systematic approximation to find the dominant terms in thin film evolution. In Section 5 we analyze the stability properties of this reduced equation and finally in Section 6 we summarize our results.
2. Model for Film Growth
We begin with the model from [6] . This model describes the evolution of a strained film due to surface diffusion in response to the driving forces of elastic strain energy and surface energy. We consider here the simple case of annealing of a film (no vapor deposition). The film lies in , the vapor in , and the substrate occupies . The vapor is taken to be at zero pressure The states of stress and strain in a deformed crystal being idealized as a continuum are characterized by symmetric second-rank tensors and , respectively, each comprising six independent components. Hooke’s law of linear elasticity for the most general anisotropic solid expresses each component of the stress tensor linearly in terms of all components of the strain tensor in the form
(1)
where is the array of elastic stiffness constants. Each of the nine equations for a stress component involves nine material parameters. The fourth-order tensor comprises 81 components. The symmetry of the stress and strain tensors further imply that the components of the stiffness tensor must satisfy . As a consequence, the number of independent elastic constants is reduced from 81 to 36. Using this fact and rewriting the stress and strain using their symmetric properties, 1 can be written in a simpler format
(2)
Cubic symmetry is a property of crystals that possess three fourfold axes of rotational symmetry, the cube axes, and four threefold axes of rotational symmetry, the cube diagonals. Alternatively, cubic symmetry may be described as invariance of material structure under a translation of a certain distance in any of three mutually orthogonal directions; these directions are usually identified as the cube axes. Consider a cubic material for which the [100], [010] and [001] cube axes are parallel to the axes of an underlying rectangular x; y; z-coordinate system. For this case, it is evident that
(3)
All the other elastic constants vanish because of the fourfold rotational symmetry of the reference axes. Hence elastic response of any cubic crystal is characterized by three independent elastic constants and the stress-strain relationship is given by
(4)
(5)
(6)
(7)
(8)
(9)
where and are the elastic stiffnesses of the material and
(10)
Here is the ith Cartesian component of the displacement vector where the index corresponds to the coordinates respectively, and indicates partial derivative with respect to the jth coordinate. The quantities are defined separately in the film (F) and substrate (S). Since mechanical equilibrium exists within the film and the substrate,
(11)
Upon substituting the formulas for stress and strain in these equations we obtain Navier’s equations for the equilibrium displacements, which is valid both in the substrate and film:
(12)
(13)
(14)
The stress balance boundary conditions at the film free surface,
(15)
where
(16)
is the unit normal to the film surface and at the film-substrate interface read
(17)
The substrate is taken to be semi-infinite, and so the strains vanish far beneath the film,
(18)
Finally on (the film/substrate interface), continuity of displacement taking into account the lattice mismatch ò is
(19)
The evolution equation is given by surface diffusion in response to a chemical potential μ,
(20)
where the surface Laplacian,
(21)
D is a constant related to surface diffusion, and the surface chemical potential is
(22)
where E is the elastic energy density, represents the surface energy, and is the wetting energy. In the above,
(23)
and the curvature of the film κ is given by
(24)
For the wetting energy we use the two-layer wetting model where the surface energy depends on the film thickness according to
(25)
The model for the wetting energy is from [30] , based on a surface energy which depends on the film thickness and undergoes a rapid transition from to over a length scale δ:
(26)
which gives the wetting term,
(27)
where
(28)
and
(29)
Hence we get
(30)
Equation (20) is a non-linear moving boundary problem coupled to partial differential equations for the elasticity problem (12)-(19).
3. Steady State Solutions
The governing equations in Section 2 describe the stress state and surface evolution of an epitaxially strained film. They have a basic-state solution corresponding to a completely relaxed, stress-free substrate,
(31)
and a planar film with spatially uniform stress and strain,
(32)
(33)
where
(34)
which is the biaxial modulus in the plane with normal in the (001) material direction (in our case (001) material direction is the direction parallel to the z-axis).
The total elastic energy store in the film due to epitaxial and wetting stresses is
(35)
In Section 5 we perform a linear stability analysis of this basic state of an epitaxial film.
4. Nondimensional Anisotropic Governing Equations
Here we derive the evolution equation based on approximation that wavelength of surface undulations is large compared to the characteristic film thickness . Define
(36)
where l is characteristic length scale in . Let us use the following scalings:
(37)
Next let us write the elastic stresses, strains and elastic energy density as expansions in α:
(38)
(39)
(40)
Expanding the other quantities in (9) we obtain
(41)
and the surface Laplacian has the expansion,
(42)
We choose the time scale τ as
(43)
and length scale l as
(44)
We also assume that the characteristic film thickness is much larger than the wetting layer thickness, so
(45)
Hence (30) can be written as:
(46)
To balance the wetting energy term with the surface energy term in (20) we choose
(47)
and define
(48)
where . Then defining
(49)
we obtain
(50)
where
(51)
(52)
We substitute these expansions into the evolution Equation (20) to obtain
(53)
where
(54)
and
(55)
Equation (53) is the thin film evolution equation. It depends on elastic response through and , which we now determine.
4.1. Elastic Response of Film
Now we find by solving the elasticity problem. Using scalings given in (37), (12)-(14) can be written as:
(56)
(57)
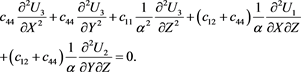 (58)
(58)
The same way we can write stress and strain using (37) and from the boundary condition (15) we obtain:
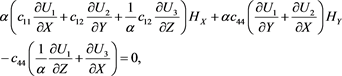 (59)
(59)
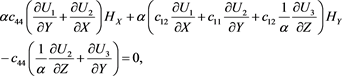 (60)
(60)
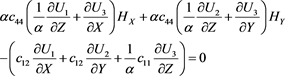 (61)
(61)
on .
.
We proceed by finding elasticity solutions in the film satisfying the boundary condition on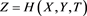 . These solutions have unknown constants to be determined from the boundary conditions on
. These solutions have unknown constants to be determined from the boundary conditions on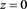 . Then we construct elasticity solutions in the substrate to determine these constants. Finally we substitute the final elasticity solutions into evolution equation.
. Then we construct elasticity solutions in the substrate to determine these constants. Finally we substitute the final elasticity solutions into evolution equation.
Now let us expand the displacements U in a,
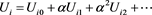 (62)
(62)
We substitute (62) in (56)-(58) and compare by order in a.
At  we obtain:
we obtain:
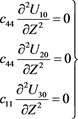 (63)
(63)
with the boundary conditions,
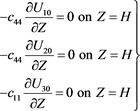 (64)
(64)
We expect the  strain tensor is
strain tensor is
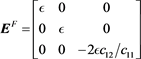 (65)
(65)
and solving (63) and using (64) we obtain 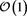 solution:
solution:
 (66)
(66)
Solving the  differential equations we obtain
differential equations we obtain
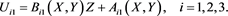 (67)
(67)
Using 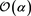 boundary conditions,
boundary conditions,


and

The same way using the 

And the 


and

Returning to our expansion for 

and

4.2. Elastic Response of Substrate
The functions 




The elasticity Equations (12)-(14) and far field condition (18) become



and

Using the Fourier transform to define 


Then using (82) we write (78)-(80) as


and

in

We expand displacement in the substrate using powers in a,

with

Using (87) and the solution for 

Using (86), (89) and (19), an 

The 

where 



using (88) and (90)

The second boundary condition is (17). At 


and

which gives us a linear system of equations for 



and

Solving (97), (98) and (99) we obtain



Hence the Fourier transform 

where

Hence in nondimensional form,

Note that the constant E contains the interaction of the elastic response of the anisotropic film and isotropic substrate.
The evolution equation at 

where

with the strength of the wetting energy quantified by

Equation (106) contains the dominant effects for thin films, derived in a self-consistent thin film approximation. The three terms on the right hand side, correspond to elastic energy (


5. Linear Stability Analysis
To determine the stability of planar films of thickness 



We consider

When the film wets the substrate, 
In Figure 2 we plot the neutral stability condition 


Figure 1. Linear stability growth rate σ versus the wave number a.
Figure 2. Schematic of the stability diagram for the film thickness 
which every film thickness is stable,

and there is a critical wave number, 

The evolution equation thus has the property that sufficiently thin films are stabilized by the wetting effect, but thicker films are unstable to the stress driven morphological instability.
6. Summary
We derived a self-contained evolution equation where the film thickness is smaller than wavelength of surface variations. Our evolution equation includes effects of anisotropic elastic constants for cubic symmetry in the film and isotropic elastic constants in the substrate, isotropic surface energy, and wetting energy. This evolution equation possesses steady state solutions corresponding to island formation, and is a possible candidate for use in large scale simulations of island systems.
Acknowledgements
Sincere thanks to the members of JAMP for their professional performance. And W. Tekalign would like to thank his Ph.D. adviser Dr. Brian J. Spencer for his valuable inputs and support throughout the years.
Cite this paper
Tekalign, W. and Atena, A. (2018) Thin Film Evolution Equation for a Strained Anisotropic Solid Film on a Deformable Isotropic Substrate. Journal of Applied Mathematics and Physics, 6, 864-879. https://doi.org/10.4236/jamp.2018.64074
References
- 1. Kastner, M.A. (1996) Mesoscopic Physics with Artificial Atoms. Proceedings of the 23rd International Conference on Physics of Semiconductors, 1, 27.
- 2. Chen, M. and Porod, W. (1995) Design of Gate-Confined Quantum-Dot Structures in the Few-Electron Regime. Journal of Applied Physics, 78, 1050. https://doi.org/10.1063/1.360339
- 3. Asaro, R.J. and Tiller, W.A. (1972) Interface Morphology Development during Stress Corrosion Cracking: Part I. via Surface Diffusion. Metallurgical and Materials Transactions B, 3, 1789-1796. https://doi.org/10.1007/BF02642562
- 4. Grinfeld, M.A. (1986) Instability of the Interface between a Non-Hydrostatically Stressed Elastic Body and a Melt. Doklady Akademii Nauk SSSR Sov.Phys. Dokl. 31, 831.
- 5. Srolovitz, D.J. (1989) On the Stability of Surfaces of Stressed Solids. Acta Metallurgica, 37, 621-625. https://doi.org/10.1016/0001-6160(89)90246-0
- 6. Spencer, B.J., Voorhees, P.W. and Davis, S.H. (1991) Morphological Instability in Epitaxially Strained Dislocation-Free Solid Films. Physical Review Letters, 67, 3696. https://doi.org/10.1103/PhysRevLett.67.3696
- 7. Daruka, I., Tersoff, J. and Barbasi, A.L. (1999) Shape Transition in Growth of Strained Islands. Physical Review Letters, 82, 2753. https://doi.org/10.1103/PhysRevLett.82.2753
- 8. Nix, W.D. (1989) Mechanical Properties of Thin Films. Metallurgical and Materials Transactions A, 20A, 2217. https://doi.org/10.1007/BF02666659
- 9. Gao, H. (1991) Stress Concentration at Slightly Undulating Surfaces. Journal of the Mechanics and Physics of Solids, 39, 443-458. https://doi.org/10.1016/0022-5096(91)90035-M
- 10. Gao, H. (1991) A Boundary Perturbation Analysis for Elastic Inclusions and Interfaces. International Journal of Solids and Structures, 28, 703-725. https://doi.org/10.1016/0020-7683(91)90151-5
- 11. Grinfeld, M.A. (1993) The Stress Driven Instability in Elastic Crystals: Mathematical Models and Physical Manifestations. Journal of Nonlinear Science, 3, 35-83. https://doi.org/10.1007/BF02429859
- 12. Berrehar, J., Caroli, C., Lapersonne-Meyer, C. and Schott, M. (1992) Surface Patterns on Single-Crystal Films under Uniaxial Stress: Experimental Evidence for the Grinfeld Instability. Physical Review B, 46, 13487. https://doi.org/10.1103/PhysRevB.46.13487
- 13. Jesson, D.E., Pennycook, S.J., Baribeau, J.M. and Houghton, D.C. (1993) Direct Imaging of Surface Cusp Evolution during Strained-Layer Epitaxy and Implications for Strain Relaxation. Physical Review Letters, 71, 1744. https://doi.org/10.1103/PhysRevLett.71.1744
- 14. Yang, W.H. and Srolovitz, D.J. (1994) Surface Morphology Evolution in Stressed Solids: Surface Diffusion Controlled Crack Initiation. Journal of the Mechanics and Physics of Solids, 42, 1551-1574. https://doi.org/10.1016/0022-5096(94)90087-6
- 15. Spencer, B.J. and Meiron, D.I. (1994) Nonlinear Evolution of the Stress Driven Morphological Instability in a Two Dimensional Semi-Infinite Solid. Acta Metallurgica et Materialia, 37, 621.
- 16. Xiang, Y. and Weinan, E. (2002) Nonlinear Evolution Equation for the Stress-Driven Morphological Instability. Journal of Applied Physics, 91, 9414. https://doi.org/10.1063/1.1477259
- 17. Spencer, B.J. and Tersoff, J. (1996) Equilibrium Shapes of Small Strained Islands. Materials Research Society Symposia Proceedings, 399, 283-288. https://doi.org/10.1557/PROC-399-283
- 18. Spencer, B.J. and Tersoff, J. (1997) Equilibrium Shapes and Properties of Epitaxially Strained Islands. Physical Review Letters, 79, 4858-4861. https://doi.org/10.1103/PhysRevLett.79.4858
- 19. Kukta, R.V. and Freund, L.B. (1997) Minimum Energy Configuration of Epitaxial Material Clusters on a Lattice-Mismatched Substrate. Journal of the Mechanics and Physics of Solids, 45, 1835-1860. https://doi.org/10.1016/S0022-5096(97)00031-8
- 20. Rudin, C.D. and Spencer, B.J. (1999) Equilibrium Island Ridge Arrays in Strained Solid Films. Journal of Applied Physics, 86, 5530-5536. https://doi.org/10.1063/1.371556
- 21. Shanahan, L.L. and Spencer, B.J. (2002) Interfaces and Free Boundaries. Interfaces and Free Boundaries, 4, 1-25. https://doi.org/10.4171/IFB/50
- 22. Tekalign, W.T. and Spencer, B.J. (2007) Thin-Film Evolution Equation for a Strained Solid Film on a Deformable Substrate: Numerical Steady States. Journal of Applied Physics, 102, Article ID: 073503. https://doi.org/10.1063/1.2785024
- 23. Zhang, Y.W. and Bower, A.F. (1999) Numerical Simulations of Island Formation in a Coherent Strained Epitaxial Thin Film System. Journal of the Mechanics and Physics of Solids, 47, 22730-2297. https://doi.org/10.1016/S0022-5096(99)00026-5
- 24. Bergamaschini, R., Salvalaglio, M., Backofen, R., Voigt, A. and Montalenti, F. (2016) Continuum Modelling of Semiconductor Heteroepitaxy: An Applied Perspective. Advances in Physics, 1, 331-367.
- 25. Liu, P., Zhang, Y.W. and Lu, C. (2003) Coarsening Kinetics of Heteroepitaxial Islands in Nucleationless Stranski-Krastanov Growth. Physical Review B, 68, Article ID: 035402. https://doi.org/10.1103/physrevb.68.035402
- 26. Golovin, A.A., Davis, S.H. and Voorhees, P.W. (2003) Self-Organization of Quantum Dots in Epitaxially Strained Solid Films. Physical Review E, 68, Article ID: 056203. https://doi.org/10.1103/PhysRevE.68.056203
- 27. Tekalign, W.T. and Spencer, B.J. (2004) Evolution Equation for a Thin Epitaxial Film on a Deformable Substrate. Journal of Applied Physics, 96, 5505-5512. https://doi.org/10.1063/1.1766084
- 28. Pang, Y. and Huang, R. (2006) Nonlinear Effect of Stress and Wetting on Surface Evolution of Epitaxial Thin Films. Physical Review B, 74, Article ID: 075413. https://doi.org/10.1103/PhysRevB.74.075413
- 29. Levine, M.S., Golovin, A.A., Davis, S.H. and Voorhees, P.W. (2007) Self-Assembly of Quantum Dots in a Thin Epitaxial Film Wetting an Elastic Substrate. Physical Review B, 75, Article ID: 205312. https://doi.org/10.1103/PhysRevB.75.205312
- 30. Spencer, B.J. (1999) Asymptotic Derivation of the Glued-Wetting-Layer Model and Contact-Angle Condition for Stranski-Krastanow Islands. Physical Review B, 59, 2011. https://doi.org/10.1103/PhysRevB.59.2011



