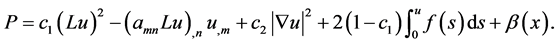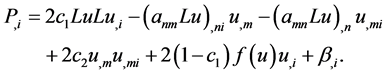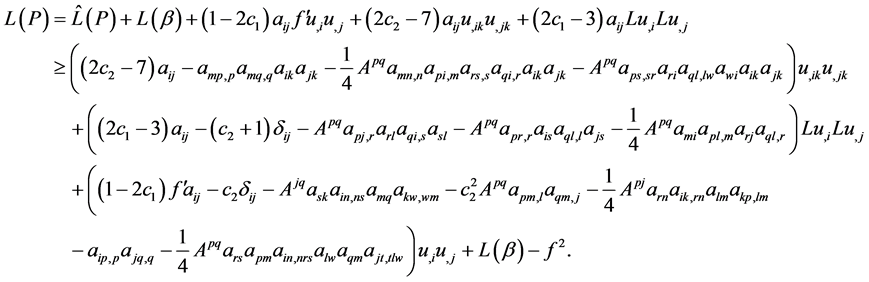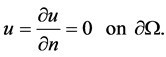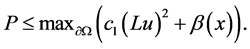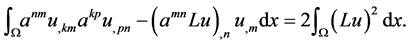Journal of Applied Mathematics and Physics
Vol.04 No.08(2016), Article ID:70202,5 pages
10.4236/jamp.2016.48176
A Maximum Principle Result for a General Fourth Order Semilinear Elliptic Equation
A. Mareno
Penn State University, Middletown, USA

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 June 2016; accepted 27 August 2016; published 30 August 2016
ABSTRACT
We obtain maximum principles for solutions of some general fourth order elliptic equations by modifying an auxiliary function introduced by L.E. Payne. We give a brief application of these maximum principles by deducing apriori bounds on a certain quantity of interest.
Keywords:
Nonlinear, Fourth Order, Partial Differential Equation, Semilinear

1. Introduction
In [1] , Payne obtains maximum principle results for the semilinear fourth order elliptic equation
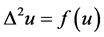 (1)
(1)
by proving that certain functionals defined on the solution of (1) are subharmonic. In this work, functionals containing the terms  are utilized and apriori bounds on the integral of the square of the second gradient and on the square of the gradient of the solution are deduced. Since then, many authors [2] - [11] and references therein have used this technique to obtain maximum principle results for other fourth order elliptic differential equations whose principal part is the biharmonic operator.
are utilized and apriori bounds on the integral of the square of the second gradient and on the square of the gradient of the solution are deduced. Since then, many authors [2] - [11] and references therein have used this technique to obtain maximum principle results for other fourth order elliptic differential equations whose principal part is the biharmonic operator.
Other works deal with the more general fourth order elliptic operator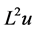 , where
, where 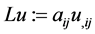 and
and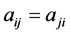 . In [12] , Dunninger mentions that functionals containing the term
. In [12] , Dunninger mentions that functionals containing the term  can be used to obtain maximum principle results for such linear equations as
can be used to obtain maximum principle results for such linear equations as

A similar approach is taken in [13] for a class of nonlinear fourth order equations.
In this paper, we modify the results in [1] and a matrix result from [14] to deduce maximum principles defined on the solutions to semilinear fourth order elliptic equations of the form:
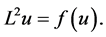 (2)
(2)
Then we briefly indicate how these maximum principles can be used to obtain apriori bounds on a certain quantity of interest.
2. Results
Throughout this paper, the summation convention on repeated indices is used; commas denote partial differentiation. Let 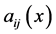 be a symmetric matrix. Moreover let
be a symmetric matrix. Moreover let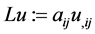 , be a uniformly elliptic operator, i.e, the symmetric matrix
, be a uniformly elliptic operator, i.e, the symmetric matrix 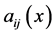 is positive definite and satisfies the uniform ellipticity condition:
is positive definite and satisfies the uniform ellipticity condition: 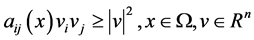 , where
, where  is a bounded domain in
is a bounded domain in 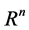 and
and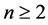 .
.
Let u be a 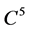
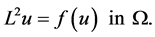
where f is say, a 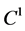
We show that 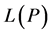
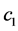
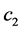
By a straight-forward calculation, we have
Now we write
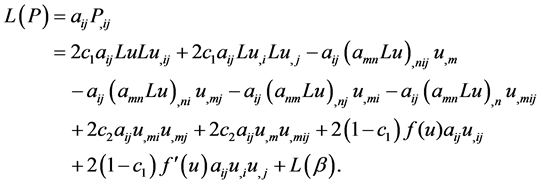
By expanding out the derivative terms in parentheses, we see that 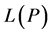
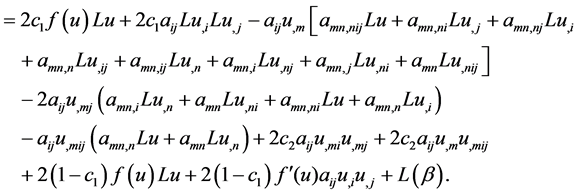
The terms in lines 2 and 3 above containing two or more derivatives of 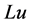
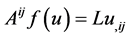
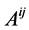
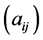
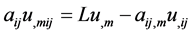
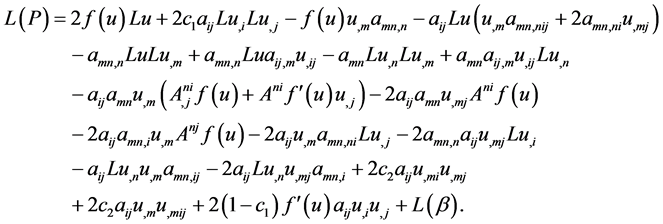
Using the identity above for 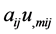
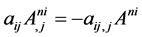
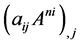
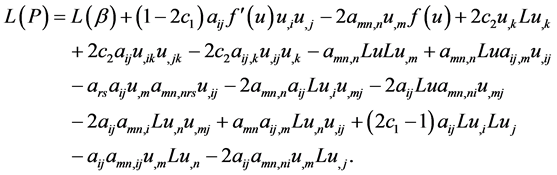
To show that 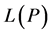
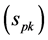
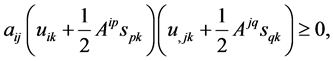
One can deduce
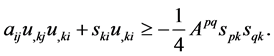
Repeated use of (9) on terms in lines 2, 3, 4, 5 in (7) yields the following:
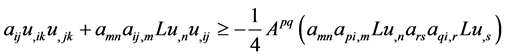
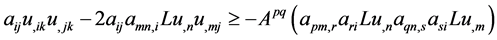
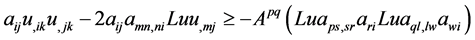
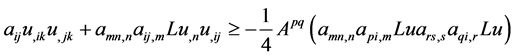
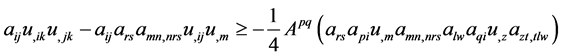
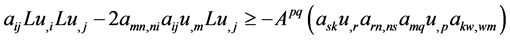
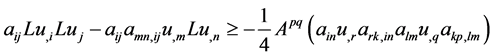
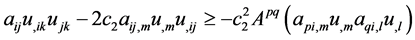
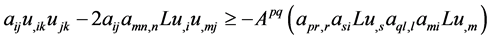
Furthermore, by completing the square, we obtain useful inequalities for the last two terms in line 1 and the third term in line 2 of (7):
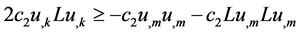
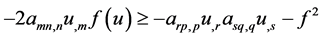
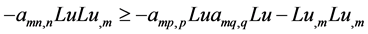
We add (10)-(21) and label the resulting inequality, for part of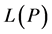
Now,
Since 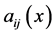
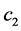
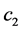
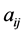
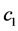
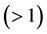
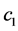
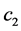
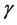
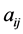
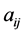
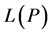
Theorem 1. Suppose that 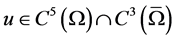
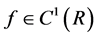
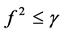
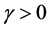
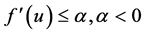
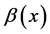
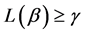
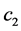
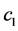
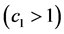
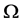
We note that the function 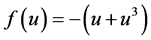
3. Bounds
Here we give a brief application of Theorem 1.
Suppose that
By Theorem 1,
Using integration by parts on the first two terms of P yields the identity
Upon integrating both sides of the previous inequality we deduce
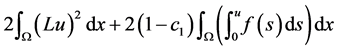
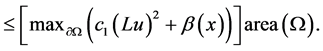
Cite this paper
A. Mareno, (2016) A Maximum Principle Result for a General Fourth Order Semilinear Elliptic Equation. Journal of Applied Mathematics and Physics,04,1682-1686. doi: 10.4236/jamp.2016.48176
References
- 1. Payne, L.E. (1976) Some Remarks on Maximum Principles. Journal d’Analyse Mathematique, 30, 421-433.
http://dx.doi.org/10.1007/BF02786729 - 2. Danet, C.-P. (2014) Two Maximum Principles for a Nonlinear Fourth Order Equation from Thin Plate Theory. Electronic Journal of Qualitative Theory of Differential Equations, 31, 1-9.
- 3. Danet, C.P. (2011) Uniqueness in Some Higher Elliptic Boundary Value Problems in n Dimension Domain. Electronic Journal of Qualitative Theory of Differential Equations, 54, 1-12.
- 4. Dhaigude, D.B., Dhaigude, R.M. and Lomte, G.C. (2012) Maximum Principles for Fourth Order Uniformly Elliptic Equations with Applications. International Journal of Applied Mathematical Research, 3, 248-258.
- 5. Goyal, S. and Goyal, V.B. (2011) On Some Fourth Order Elliptic Boundary Value Problems. Applied Mathematical Sciences, 36, 1781-1793.
- 6. Lomte, G.C. and Dhaigude, R.M. (2013) Maximum Principles for Fourth Order Semilinear Elliptic Boundary Value Problems. Malaya Journal of Matematik, 1, 44-48.
- 7. Lu, W.D. and Wang, J.H. (1981) Maximum Principles for Some Semilinear Elliptic Equations of Fourth Order, and Their Application. Sichuan Daxue Xuebao, 4, 33-45. (In Chinese)
- 8. Mareno, A. (2008) Maximum Principles for a Fourth Order Equation from Thin Plate Theory. Journal of Mathematical Analysis and Applications, 343, 932-937.
http://dx.doi.org/10.1016/j.jmaa.2008.02.004 - 9. Mareno, A. (2010) Integral Bounds for von Karmans Equations. ZAMM, 90, 509-513.
http://dx.doi.org/10.1002/zamm.200900325 - 10. Mareno, A. (2011) Maximum Principles for Some Higher Order Semilinear Elliptic Equations. Glasgow Mathematical Journal, 53, 313-320.
http://dx.doi.org/10.1017/S001708951000073X - 11. Zhang, H. and Zhang, W. (2002) Maximum Principles and Bounds in a Class of Fourth Order Uniformly Elliptic Equations. Journal of Physics A: Mathematical and General, 35, 9245-9250.
http://dx.doi.org/10.1088/0305-4470/35/43/318 - 12. Dunninger, D.R. (1972) Maximum Principles for Solutions of Some Fourth Order Elliptic Equations. Journal of Mathematical Analysis and Applications, 37, 655-658.
http://dx.doi.org/10.1016/0022-247X(72)90248-X - 13. Nichols, E.C. and Schaefer, P.W. (1987) A Maximum Principle In Nonlinear Fourth Order Elliptic Equations. Lecture Notes in Pure and Applied Mathematics, 109, 375-379.
- 14. Schaefer, P.W. (1987) Pointwise Estimates in a Class of Fourth-Order Nonlinear Elliptic Equations. ZAMP, 38, 477-479.
http://dx.doi.org/10.1007/BF00944964