Received 20 February 2016; accepted 25 April 2016; published 29 April 2016

ABSTRACT

The electrodynamics both in RF with prescribed law of motion and in FR with prescribed structure is considered. Parallel comparison for solutions in “uniformly accelerated” NRF Möller system and in uniformly accelerated rigid NFR in the space of the constant curvature is carried out. The stationary criterion is formulated. On the basis of this criterion, one of the “eternal physical problems” concerning the field at uniformly accelerated charge motion is considered. The problems of electromagnetic wave spreading, Doppler’s effect and field transformations are discussed.

Keywords:

Noninertial Reference Frame (NFR), Möller System, Space-Time Curvature, Anholonomic Transformations, Doppler’s Effect, Electromagnetic Wave

1. Introduction

To solve radiolocation and inertial navigation problems taking into account relativistic corrections, the analytical apparatus of relativistic non-inertial reference frames (NFR) is needed. However, in relativistic theory, a single analytical definition both reference frames and rules ascertaining a transition between them does not exist. According to physical encyclopaedia, “reference frames (FR) are collections of coordinate system and clock connected with a body relatively what a motion (or equilibrium) of some other material points or bodies is studied”… Therefore, to study a motion (equilibrium) of other bodies, the analytical specifying of a body property―the basis of RF itself is needed. In the general relativity theory (GR), we define the FR as “…a collection of infinite number of bodies filling all space like some ‘medium’ [1] ”. When considering the most elementary NFR in the special relativity theory (SR) such as uniformly accelerated and uniformly rotating ones, we face logical difficulties. Let us consider these difficulties in a uniformly accelerated NFR.

One assumes [2] that the transition to a rigid uniformly accelerated NFR is realized by means of the known Möller transform. However [3] , the situation when an acceleration of all medium particles in the co-moving FR is constant and identical and the congruency of the world lines is a Born-rigid is impossible. The analysis of the Möller transform shows that in the Fermi-Uolker basis to which the accelerometer readings are related [4] , the accelerations of different particles are not identical. They are calculated in accordance with the formula

,

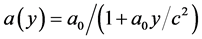where 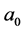is the particle acceleration along the y axis located at the origin of the Lagrangian co-moving coordinate system; c is the velocity of light in a free space. Thus, the Möller transform does not describe the transition to the globally uniformly accelerated NFR. Each Lagrangian particle moves with constant acceleration, but these accelerations are not equal each other [5] .

The Logunov transform [6] is an alternative of the Möller transform describing the transition from the inertial reference frame (IFR) to relativistic uniformly accelerated NFR where each Lagrangian basis particle moves with constant acceleration. Such reference frame can be realized when considering charged non-interacting each other similar dust particles moving with zero initial velocity in uniform electric field. However, if one calculates by means of standard procedure [1] three-dimensional metric tensor specified at the hyper surface orthogonal to the world lines of basis particles, one can be convinced that “physical” space distance between adjacent world lines will increase with time. Thus, the globally uniformly accelerated Logunov system is not a Born-rigid.

We obtain a paradoxical result. Similar physical situation for all particles resulted in a motion of the particles relatively each other (the Logunov system). In order to make these particles be mutually immovable, the different forces are needed (the Möller system).

One can show the paradoxicality of such situation on an illustrative example.

Let two identical automobiles connected with a fragile weightless rod simultaneously start along x axis. This rod breaks if in the reference frame, connected with the rod, the distance between these automobiles changes. This rod breaks if at the distance to accelerate the engines deliver identical thrust (the Logunov system), and the rod does not break if the second automobile delivers higher power than the first one (the Möller system). The known Bell paradox is connected with this situation. In [7] - [9] , it is shown that the Bell paradox is solved only by means of the transition to Riemannian space-time without the connection with the Einstein equations.

The description of rigid NFR in SR results in logical difficulties, which one overcomes by means of going out of a flat space-time. Similar ideas were expressed by V. I. Rodichev.

All NFR are divided into two classes:

1) NFR with specified law of motion.

2) NFR with specified structure.

The routine method of transition from IFR to NFR [10] is connected with the non-linear transformation of coordinates containing the time, i.e. with the law of continuum motion in the Lagrangian coordinates, for example, by means of integration of motion equations in Euler variables.

It is clear that if the motion equations were specified in Minkowski space then one cannot exceed the limits of flat space-time by no transformations of coordinates both containing the time and non-containing the time as one cannot obtain the nonzero Riemann-Christoffel tensor if it was absent in IFR. Such NRF are the first class NFR. However, in NFR of the first class one can introduce the nonzero relative Riemann tensor! (This is our terminology.) If one uses non-holonomic transformations from IFR to NFR in accordance with Shouten [11] , we also obtain zero curvature tensor. However, from this zero tensor one can obtain the general Riemann tensor with the holonomic connectedness, which is called the relative curvature tensor. In our opinion the mistake in transition to the first class NFR is connected with the misapplication of the transition formula from the Lagrange coordinates to the Euler coordinates

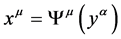. (1.1)

The Greek indices will run values from 1 to 4. The Latin indices values from 1 to 3. Wherein is the cause of error? In classical mechanics of continua the transition into Lagrangian co-moving NFR is derived at the fixed instant of time t. In relativistic continuum mechanics the total differential 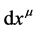is derived and the element of physical spatial distance is constructed

. (*)

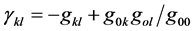In regard to the time domain element, in our opinion the factors 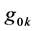are unnecessary. It is clear that in our calculation method

.

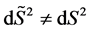This results in the interval element

. (1.2)

It is clear that in our case the physical space and the time are orthogonal. For example, rotating nonrelativistic NFR is represented in the form

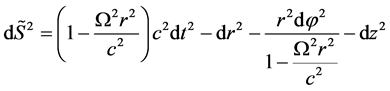. (1.3)

To compare we present interval value in the standard consideration

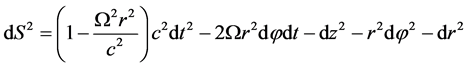. (1.4)

Both formulas are correct if and they satisfy to the stiffness criterion both classic and relativistic one (in Born sense). However, there is the essential difference between these metrics: metric (1.3) is realized in Riemannian space-time and metric (1.4) is realized in plane Minkovsky space. At 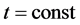metric (1.3) corresponds to the element of “physical” spatial interval in revolving reference frame in accordance with formula (*). In (1.3) unlike (1.4) 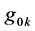components of metric tensor are absent, this means the possibility of watches synchronization along any closed circuit [1] .

A continuous medium in the four-space-time is described by the following characteristics: the four-accelera- tion, the strain-rate tensor, and the tensor of angular velocity of rotation. The four-acceleration enters the motion law, and, with a known flat metric, integration of the motion equation yields the four-velocity field and the fundamental tensors of the medium. For the frames of reference with properties specified by physical requirements, one must know additional conditions imposed on the fundamental tensors of the medium, which depend on four-velocities and four-accelerations. An example is the requirements to the rotation and rigidity. The number of equations for determining the four-velocity is over determined; therefore, the integrability conditions must be satisfied. This will held true if not only the four-velocities of the medium but also the metric coefficients are desired values.

In NFR of the second class not only knowledge of law of continuum motion is needed, but the properties of FR are specified beforehand. These properties are determined with the strain-rate tensor and the tensor of angular velocity of rotation.

In description the properties of arbitrary deformed reference frames in the form of continuum either the field of four-velocity (Euler’s view point) or the law of continuous medium motion establishing a connection between Euler and Lagrangian variables is specified. Space-time is considered either plane in the case of SR or Riemannian in the case of general relativity (GR). If one can neglect with gravitational interaction between the particles and external force acting on the body is not a gravitational one then to describe a medium motion SR relativistic mechanics is applied. In SR the fields do not distort the space-time both in IRF and in co-moving NFR of continuum keeping its space-time geometry as a plane. Only “space sections” are bent. The geometry of the sections in the general case ceases to be Euclidean geometry. Such viewpoint is the most widespread in theory of relativity.

Works of V. I. Rodichev [12] and A. A. Vlasov [13] stand apart from standard interpretation. In [13] considering the theory of growth of crystalline, plasma and biological structures with conservation of their similarity the author ascertained that growth of such structures is possible in non-Euclidean space time. It is provided to be that Minkowski space is “tight” in order to simultaneously satisfy the simplest requirements: Born rigidity and uniformly acceleration.

Our approach is based on development and modernization of Rodechev’s and Vlasov’s ideas and it includes the following:

Let continuum is at rest in a plane Minkovsky space-time with signature (+ − − −). In some instant of time 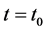any force field (except gravitational one) switches on and the continuum starts moving. What properties of space-time will be after switching on the force field? In accordance with the orthodox version space-time properties will be invariable [6] . Our answer this question will not be so categorical. We assume that switching on of force field can change space-time property transforming it to curved one in limits of world tube.

We want to determine that structure on prescribed structure of force field and also on such continuum characteristics as tensor of deformation rate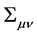, tensor of angular rotational velocity, first curvature vectors of world lines of medium particles (equations of motion).

Let us assume that a continuous medium moves in four-dimensional space-time with signature (+ − − −). The medium satisfies the expansion

. (1.5)

Here, V_μ is the field of four-velocity, which satisfies the normalization condition

. (1.6)

g_μν is the metric tensor in the Euler frame of reference; Σ_μν is the strain-rate tensor; Ω_μν is the tensor of angular velocity of rotation; and F_μ are the first curvature vectors of the world lines of particles of the medium (four- accelerations):

, (1.7)

, (1.8)

. (1.9)

The Greek indices run values from 0 to 3. The Latin indices values from 1 to 3. Expansion (1.5) can be interpreted from the following two points of view:

1) The field of four-velocity V_μ is assumed to be known, for example, as a result of integration of the Euler or the Navie-Stokes relativistic motion equation at a specified flat metric. The continuum characteristics Σ_μν, Ω_μν, and F_μ can be obtained from Formulas (1.7) to (1.9), and expansion (1.5) turns to identity.

2) The functions Σ_μν, Ω_μν, and F_μare assumed to be specified. Expansion (1.5) is transformed into a system of differential equations with respect to V_ν and g_μν. The number of Equations (1.5) and (1.6) exceeds the number of unknown functions; therefore, the integrability conditions must be satisfied:

. (1.10)

To determine the relationship between the geometric and kinematic characteristics of the continuum, we will calculate the expression

with allowance for (1.5) to (1.10), it follows from this expression that

(1.11)

Integration of System (1.5), (1.11), where is the curvature tensor (which is conventionally expressed in terms of the metric tensor), yields a solution to the problem on the space-time geometry, in which an NFR with a specified structure is implemented. Equation (1.11) will be referred to as structural equations for the frame of reference [1] . The metric of a linearly accelerated NFR takes the form

(1.12)

where the acceleration is directed along the axis [1] . The linear acceleration of NFR (1.12) can be verified directly:

(1.13)

The other components of the four-acceleration are zero. Let us find the space-time geometry in the NFR using the known formula for the curvature tensor [1]

, (1.14)

where the Christoffel’s symbols are calculated in accordance with the formulas

, (1.15)

. (1.16)

The single independent component of the curvature tensor, calculated from metric (1.12), has the form

. (1.17)

The components of the Ricci tensor can be written as

, ,. (1.18)

and the scalar curvature is

. (1.19)

Thus, one can realize the relativistic rigid uniformly accelerated NRF in a space of constant curvature.

Substitution of the value (which corresponds to the Möller’s metric [5] ) instead of metric (1.12) into the right-hand side of (1.17) yields. One would expect this result, because the Möller’s metric is obtained by transforming the coordinates from the Minkowski space. In the case under consideration, the joint requirement of rigidity and linear acceleration does not turn the right-hand side of structural equations (1.11) to zero, as a result of which the Riemann−Christoffel tensor is nonzero. Formulas (1.12) and (1.17) were derived in [1] and these ones were repeated in [14] [15] . The problems of electrodynamics in NRF of the first and second class are considered in this article.

2. Electrodynamics in NRF with Prescribed Law of Motion

Let us apply the theory of transition to arbitrary NRF determined with the law of motion ( [16] , (10.1)) for the transformation of electrodynamic equations from IRF to NRF.

Let the continuum motion law in an arbitrary force field in Minkowski space is determined by the equations

, (10.1)

where are the Eulerian coordinates and are the Lagrangian coordinates which are constant along each fixed world line, is some time parameter, for example, proper time. Let us agree that indices belong to Eulerian coordinates and indices belong to Lagrangian coordinates.

The Maxwell equations in vacuity in IRF Cartesian coordinates have the form [1]

, ,. (2.1)

In Correlation (2.1), is the tensor of electromagnetic field; is the four-dimensional current vector; is the 4-potential.

The transition to the NRF realized by means of ( [16] , (10.1), (10.2))

, ,

,. (10.2)

results in equations

, ,

, , , (2.2)

where

,. (2.2a)

It follows from Formula (2.2) that absolute tensor of electromagnetic field is decomposed on the relative tensor of electromagnetic field and the “transposed” one. The relative field tensor can be presented in the form

, (2.3)

where is calculated by means of the Christophel’s part of the connectedness ( [16] , (10.6)).

(10.6)

Transferable field tensor is the product of scalar potential and nonholonomity object, i.e. it contains information about an acceleration and reference frame rotation in accordance with ( [16] (10.11))

, ,. (10.11)

We point out, that the partition of the field tensor on two parts is conditional, since the field information in the form of the scalar potential is contained and in the “transposed” field. Let us rewrite the Maxwell equations in more detail.

We present the first Equation (2.2) in the form

,

.

Whence after simple transformations we obtain

,

, (2.4)

where is the covariant derivative calculated by means of three-dimensional Christophel connectedness; is the scalar charge density,. It is known that potentials are determined ambiguously. For example, known Lawrence conditions in Galilean coordinates having the form

, (2.5)

will reduce in NRF to the form

. (2.6)

Let us introduce three-dimensional vector of electric intensity, vector of electric induction, vector magnetic intensity and vector of magnetic induction in accordance with determinations borrowed from the Maxwell equations in NRF for the specified gravitational field [2] with the substitution of partial derivatives by directional ones

, , ,. (2.7)

Unlike [1] the metric is synchronous ( [16] , (10.9))

, ,. (10.9)

We introduce vector operations in accordance with determinations:

, ,

, ,

,. (2.8)

In (2.8)

, , ,

where is the unit antisymmetric tensor in curvilinear coordinates.

On the basis of made remarks the Maxwell Equation (2.2) in the reference system connected with the moving charges ( [16] , (10.1)) on which arbitrary forces (unnecessary electromagnetic ones) act will reduce to the form

, ,

,. (2.9)

The Maxwell equations are added with continuity equations expressing the charge conservation law

. (2.10)

We point out that unlike the general Maxwell Equation (2.2) suitable for arbitrary NRF unnecessary connected with moving charges, in Equation (2.9) (because of concomitance) the space component of 4-current is absent. This component should be added when considering the general case.

Found three-dimensional form of the Maxwell equations obtained by means of nonholonomic transformations coincides with the three-dimensional chronometrically invariant form presented in N.V. Mitskevich book [17] .

To solve the set of the Maxwell equations it is convenient to introduce electric field potentials. Let us present some necessary formulas obtained from the nonholonomic vector analysis to transit from field strength to potentials. For arbitrary three-dimensional vector field and scalar field following correlations are valid:

,

, ,

,

. (2.11)

The values included in (2.11) are determined in ( [16] , (10.38))

(10.38a)

In accordance with determination (2.7) let us present electric and magnetic intensities in a vector form via potentials in the form

. (2.12)

. (2.13)

Expressions (2.12) and (2.13) reduce the first and the fourth Equation (2.9) to an identity. This follows directly from (2.1) when the second Equation (2.1) is satisfied identically, if the tensor of electromagnetic field is expressed via delayed potentials in the form.

We will express two other Maxwell equations from (2.9) via delayed potentials. We take into account correlations (2.11) and kinematics identities ( [16] , (10.17), (10.34))

(10.17)

(10.34)

which we will present in the vector form

,. (2.14)

Taking into account the Lawrence Conditions (2.6) after enough tiresome transformations we obtain

(2.15)

(2.16)

In Formulas (2.15) and (2.16)

(2.17)

is the chronometrically invariant space-covariant D’Alembert operator and tensor, where is the three-dimensional curvature tensor determined from ( [16] , (10.31)).

(10.31)

Derived equations are valid in arbitrary deformed NRF connected with moving charges forming the continuum. It is clear to solve equations in NRF in general form is difficult, however in some particular cases the experimentation in NRF is significantly simpler and more evident than in IRF.

3. Stationary Criterion in NRF with Prescribed Law of Motion

It is interesting to investigate the Maxwell equations in relativistic rigid NRF determined as

. (3.1)

This results in the form of the Maxwell equations

. (3.2)

(3.2a)

Let us find out which properties a rigid NRF with “trapped” charges should have in order to the Maxwell system permitted time independent solutions in it? (We consider that external fields are absent and the field is determined only by “trapped” charges.) Obviously the Maxwell equations can have stationary solutions relatively rigid NRF, if characteristics determining NRF do not explicitly depend on time. i.e., at zero tensor of deformation velocities (3.1) Conditions (3.3) have to be met:

,. (3.3)

In accordance with the identity ( [16] , (10.17)), (3.3) and equalities, we have

. (3.4)

Whence

, (3.5)

that gives

. (3.6)

Equality (3.6) determines Lorentz―covariant stationary condition of possible solutions of the Maxwell equations.

Multiplying (3.6) by provided that we obtain the equality

. (3.7)

Let us introduce 4-vector of force determined with the equality

(3.8)

and we name it as generalized force of radiation friction. In this equality e is the charge of the particle “trapped” in NRF (to simplify we consider only identical particles).

For one charge moving progressively and generalized force passes to usual braking force with the radiation [1] . If the electromagnetic field in NRF is stationary then.

Let us find out what simplest NRF satisfy to stationary conditions formulated.

a) Let us consider the rectilinear rigid in Born sense uniformly accelerated (for each fixed medium particle) continuum motion. As it has been showed [16] the progressive medium displacement obtained by means of the Möller transformation satisfies to such motion.

For Möller transformation the law of motion has the form ( [16] , (2.11))

(2.11)

and Möller metric is expressed with the interval element ( [16] , (2.12))

(2.12)

here with the parameter numbering the hyper surfaces orthogonal to world lines of the basis particles plays the time role T [3] . As in Möller transformations the space vectors connecting two any close Lagrange particles remain in the “physical” space, then the transition to the Möller NRF in accordance with the developed transition scheme one can realize by means of holonomic transformations (particular case of nonholonomic transforma-

tions). However to generalize we obtain by means of formulas ( [16] , (10.2)) taking into account and 4-velocity, following transformation factors:

, ,

, , , ,

, ,. (3.9)

We point out that the pseudoeuclidness of interval (3.9) (unlike Möller interval [16] , (2.12)) is stipulated for the obvious equality

, (3.10)

which is valid along each fixed world line of basis particles.

As it has been shown [3] one can represent the field of 4-velocity of Möller basis in Minkowski space in Euler variables in the form

. (3.11)

One can make sure with direct calculation that (3.11) satisfies to the stationary condition (3.6). Consequently, the Maxwell equations in such NRF permit the stationary solution.

One can obtain stationary Maxwell equations in such NRF from Formulas (3.2), (3.2a) and (2.11).

, (3.12)

. (3.12a)

Lorentz Condition (2.6) for stationary solutions reduces to the form

. (3.13)

To analyze we use the identity ( [16] , (10.16))

(10.16)

which for the case of rigid eddyless motions is equivalent to

. (3.14)

As for the Möller metric then comparing (3.13) and (3.14) we find the solution for the vector potential in the form

,. (3.15)

It follows from Correlations (2.13), (2.14) and Solution (3.15) that charges “trapped” in the rigid eddyless NRF for which stationary Condition (3.6) are valid do not create a magnetic field in this system i.e.

. (3.16)

Let us consider the solution of Equation (3.2) for the particular case of the point charge located at the origin of NRF coordinates. Instead of the tetrad time component from (3.9) we introduce the affine time component for which Equation (3.12) will reduce to the form

. (3.16a)

Solution of Equation (3.16a) in accompanying Möller and Whittaker systems has been obtained by Ts. I. Gutsunaev [18] . For our case we have

, (3.16b)

where.

Transition to IRF in accordance with our method we realize by the rule

We determine constant in (3.15) from the correspondence principle, this constant is equal to the charge value ?Q.

As a result of calculations using the motion law ( [16] , (2.11)) taking into account that the field of 4-velocities V¹ in Euler variables has the form (3.11) and easily examined expressions

, (3.17)

we obtain

,

,

. (3.18)

Firstly Solution (3.18) was obtained by Born [19] and later by means of retarded potentials by Schott [20] . Solution (3.18) also was obtained by Gutsunaev by means of the transition to Möller NRF and inverse transformation to IRF.

b) It is easy to check that the classic uniformly rotating RF also satisfies to the stationary Condition (3.6). Consequently for the charge system or for the one charge “trapped” to the uniformly rotating disk, i.e., with one side always “faced” to the disk centre, the generated force of the radiation friction (3.8). So Maxwell equations in such system permit the static solution.

The stationary criterion permits to reduce the Maxwell equations to the solution of one equation for the complex potential. This follows from the fact that for the stationary case vector Maxwell equations from (2.9) are invariant relatively the substitution. So one can find in two forms

, (3.19)

and vector for the stationary case will have the form

,. (3.20)

Using Identities (2.14), the Expressions (3.19) and (3.20) we find from (2.9) the expressions for scalar Maxwell equations

, (3.21)

. (3.22)

Let us introduce the complex potential in accordance with the determination

,. (3.23)

Summarizing Equation (3.21) multiplied by i up Equation (3.22) we obtain

. (3.24)

Equation (3.24) permits to find fields from charges “trapped” in relativistic rigid moving bodies.

It should be pointed out that from commutation correlations ( [16] , (10.10)) and nonholonomic objects ( [16] , (10.11))

(10.10)

(10.11)

it follows that for stationary solutions one can substitute directional derivatives by usual partial derivatives.

Let us consider the example of the stationary field calculation in a classic rigid rotating frame of reference. Let the charge or the charge system is trapped in this NRF. The Maxwell Equation (2.4) for this case are reduced to the form

,

. (3.25)

One can write down the first Equation (3.25) in the form

,. (3.26)

To solve (3.26) we use identity ( [16] , (10.33))

, (10.33)

it follows from this identity for rigid motions

, (3.27)

this is equivalent to

. (3.28)

Comparison (3.26) and (3.28) permits to find Solution (3.26) in the form

. (3.29)

Substitution (3.29) into (3.26) results in equality

, (3.30)

in particular, it follows from this equality

. (3.31)

To solve Equation (3.31) the fulfillment of integrability condition is necessary. As follows from ( [16] , (10.17)) the integrability condition will be satisfied in the case of rigid stationary motions. In particular, the classic rigid rotating RF satisfies to this condition. For this RF

. (3.32)

Let us consider in more detail the transition from IRF to classic rigid rotating NRF. We consider the IRF interval element in cylindrical coordinates

, (3.33)

For which metric tensor components and coordinates have the form

, , , ,

, , , ,

, , ,.

We assign in usual form the transition to the rotating NRF and inversely to IRF

(3.34)

The field of 4-velocities of the rotating NRF basis relatively IRF has the form

(3.34a)

We find Lame coefficients in accordance with the specified velocity law and coordinate transformations

(3.35)

Using obtained Lame coefficients we calculate metric coefficients in the rotating NRF

(3.36)

We point out that the metric obtained differs from the metric for relative interval ( [16] , (10.72))

(10.72)

with coefficient which in our case is equal to unit. This means that we select the proper time as the NRF time, and in ( [16] , (10.72)) the IRF time was used in NRF. The obtained metric using nonholonomic transformation is strongly differed from the standard metric ( [16] , (10.73)).

(10.73)

As it was pointed out earlier for stationary processes and stationary fields directional derivatives commutate that is the result of commutation correlations ( [16] , (10.13)).

(10.13)

So in differentiation one can consider these derivatives as usual partial ones.

On the assumption of made remarks we try to integrate system (3.25). The first equation of this system we nearly solved. It is necessary to determine only function. In order to determine this function we must know 4-accelerations of the rotating RF. Let us calculate beforehand Christophel symbols in the rotating NRF in accordance with formula ( [16] , (10.44)).

(10.44)

(3.37)

In IRF in cylindrical coordinates Christophel symbols will obtain from Formula (3.37) when. Using this property we calculate 4-acceleration of NRF basis relatively IRF. As the angular velocity is constant and the velocity vector and the acceleration vector are orthogonal in each point differed from zero, the only component of 4-acceleration will be equivalent to the centripetal acceleration. Obviously that

(3.38)

The component differed from zero relatively rotating NRF will be

(3.39)

This permits to integrate Equation (3.31)

(3.40)

where is the arbitrary constant which we will determine hereinafter. Thus, the solution of Equation (3.26) is reduced to the form

(3.41)

We present the second Equation (3.25) in the form

(3.42)

which after the use of the equality

(3.43)

and the opening of covariant derivatives by means of calculated Christophel symbols after simple but exhausting transformations reduce to one equation of the form

(3.44)

Equation (3.44) permits in principle to solve any problems for the system of charges “trapped” to the classical rigid uniformly rotating RF, however in order to prove the operating capacity of proposed method we will solve the simplest problem rotating a long hollow thin-walled dielectric cylinder with the electrostatic charge on the wall around the axis. It is clear that in accordance with the nature of magnetic field distribution this problem should be equivalent to the problem of magnetic field of infinite solenoid with the continuous winding. Direct current in solenoid wraps is equivalent to the convective current of the rotating cylinder. We shall find electromagnetic field outside of these charges both outside of and inside the cylinder.

Equation (3.44) for this considered problem reduces to the form

(3.45)

It is easy to check up by direct substitution that the sum of the general solution of the homogeneous Equation (3.45) and the partial solution of the inhomogeneous equation is represented in the form

(3.46)

where is the arbitrary constant which will be determined hereinafter. It is possibly to make sure that

(3.47)

Let us calculate the electromagnetic field tensor of the rotating hollow cylinder in the IRF cylindrical coordinates

(3.48)

In the last expression only and components of electromagnetic field tensor will be differed from zero, for which we have:

(3.49)

(3.50)

We point out that the last expressions for the field tensor are assigned in Minkowski space cylindrical coordinates. To compare with the standard record for the field tensor it is conveniently to transit to the Cartesian coordinates. As, , the component in the Cartesian coordinates is connected with the component in cylindrical coordinates in accordance with the law of three-dimensional tensors transformation

(3.51)

But in IRF Cartesian coordinates in accordance with the determination [1] . Hence and from (3.50) we have the expression for magnetic field

(3.52)

Let us determine and constants. We will consider the solution for electromagnetic field inside the cylinder shell. Electric field inside the cylinder in IFR should be equal to zero. Whence we find from (3.49) equating this expression to zero

(3.53)

(3.54)

One can determine constant from the external solution for electric field which (when the rotation is absent) from the correspondence principle should coincide with the static field outside of the charged cylinder. Whence when we have

(3.55)

where is the charge density per unit of the cylinder length. Thus, we obtain the expected result. Electric field inside the cylinder is equal to zero, and magnetic field is constant, differed from zero and it is equal to

(3.56)

where R is the cylinder radius. Outside of the cylinder, magnetic field is equal to zero, and electric field is differed from zero.

(3.57)

Let us calculate magnetic field value through the convection current per length unit. Obviously that, where j is the convection current through the length unit and T is the period of the cylinder rotation. Substituting in (3.56) we find

(3.58)

that exactly coincides with the field inside the infinite ideal solenoid. The detailed calculation carried out is some test problem of the legitimacy of the constructed nonholonomic apparatus of electrodynamic equations transformation from IRF into NRF and vice versa. Calculating and constants values we return to the analysis of electromagnetic field of the rotating hollow cylinder from the standpoint of the observer connected with this cylinder. Obviously that the correlation between Constants (3.53) will be correct inside the cylinder both in IRF and in NRF, however this does not result in zero electric field inside the cylinder. Electric field inside the cylinder in NRF is differed from zero and it changes in accordance with the law

(3.59)

For small the last correlation reduces to the form

(3.60)

One can see from the last formula that in NRF electric field at the centre of the cylinder is equal to zero and further it linearly increases reaching the maximum on the radius of the cylinder, however, the field at the internal boundary is a value of the order of from the field at the external boundary. Outside of the cylinder in NRF (as in IRF). So we obtain the expression for electric field

(3.61)

It follows from the last correlation that the formula is applied for the finite distances, for which. This difficulty is typical for the classic rotating RF. In our description of the rotating rigid RF presented earlier this difficulty is absent.

Let us investigate the magnetic field behavior in NRF. In accordance with (3.41)

(3.62)

is the component of the angular velocity tensor in NRF differed from zero, for this component from (3.43) we have

(3.63)

Using (3.36) and selecting the negative root for we find

(3.64)

Inside and outside of the cylinder the constant. We point out that in NRF the magnetic field is differed from zero both inside and outside of the cylinder. The physical sense of this is connected with the circumstance that magnetic field in NRF is determined with the tensor of the angle velocity of the NRF basis. This tensor is differed from zero both inside and outside of the cylinder. Magnetic field in IRF is determined by the convection currents of the rotating cylinder. It follows from the law determining the magnetic field in accordance with the specified current that magnetic field is present only inside the cylinder. In the rotating NRF the convection current is identically equal to zero and magnetic field is differed from zero in all space.

Tetrad components of the field tensor (but not affine ones) have a physical sense. As metric (3.36) is orthogonal then to construct the tetrad field one can superpose the vectors of ortho bench mark and the vectors of the affine bench mark, and the tetrad field can be written in the form

(3.65)

where the summation on axis is absent. Tetrad components of these tensors coincide with “physical” ones. For example, for the space component of the field tensor differed from zero and connected with magnetic field we have

(3.66)

We point out that the affine field component automatically coincides with the tetrad one in accordance with the metric (3.36).

Let us clear up the contribution to “absolute” magnetic field of its “relative” and “carry” constituents. From (3.26) and (3.29) we find the expression for the relative tensor of magnetic field

(3.67)

As then to compute the calculation both in internal and in external cylinder are as is sufficient. Considering that at the centre of the cylinder at zero electric intensity and that at the cylinder surface function is continuous, integrating for two different areas Equation (3.46) of the form

(3.68)

we find

(3.69)

(3.70)

This gives for internal solution

(3.71)

and for external solution

(3.72)

Both for inertial frames of reference and for noninertial ones one can constitute invariant values being constant when transforming from IRF to NRF and vice versa. It is easy to determine the form of invariants from following equalities

(3.73)

In particular for our problem of the rotating cylinder Expression (3.73) is equivalent to equality

(3.74)

One can make sure by direct test using the calculations made above for fields in IRF and NRF that for the external solution the invariant value is equal to and internal solution corresponds to invariant. Concerning the second known invariant corresponding to scalar product of electric and magnetic fields then because of orthogonality of these fields this invariant is identically equal to zero. Fulfillment of Equalities (3.74) also is the verification of the made calculations when determining the electromagnetic field.

Let us analyze obtained results. The nature of electromagnetic field of rotating hollow charged cylinder in IRF results in expected result namely: magnetic field inside the cylinder is constant and it coincides with the field of corresponding solenoid, outside of the cylinder magnetic field is absent. Electric field inside the cylinder is equal to zero and electric field outside of the cylinder coincides with the field of the charged cylinder being at rest.

The result of calculations of electromagnetic field in NRF is unexpected: usually one considers that in magnitostatics magnetic field is stipulated for an electric current. As the charged cylinder in NRF is being at rest then the current in this system is identically equal to zero. However, magnetic field in NRF is differed from zero both inside the cylinder and outside of it. The presence of almost constant magnetic field outside of the cylinder (in the real case in Formula (3.66) one can neglect as compared with the unit) and inside the cylinder coinciding with magnetic field in IRF inside the cylinder (3.56) at first thought is enough strange. However, the rotating system is noninertial with other physical laws then in IRF. Appearance of magnetic field in NRF inside the cylinder and outside of it is stipulated for the rotation which is absolute (3.62). “Relativity of the rotation” does not exist [21] . The second NRF surprise is the appearance of electric field differed from zero inside the cylinder. In accordance with (3.59) this field is the second-order term infinitesimal as compared with the external field (3.61). However, principle existence of the field inside the infinite charged hollow cylinder vanishing at the axis indicates that not only electric charges are the source of electric field in NRF. This follows from one of Maxwell Equation (2.9) in NRF, in accordance with this equation

the scalar product of vector of angular velocity and vector of magnetic field can be the source of electric field.

Let us compare obtained results and results of other works. In [22] [23] the expression for transformation of electromagnetic fields is presented. This transformation has the form

(3.75)

(3.76)

In Formulas (3.75) and (3.76) the primed values relate to the rotating NRF and non-primed values relate to IRF. For our problem of rotating charged hollow cylinder the last terms in presented formulas disappear as the fields of RF velocities are orthogonal to the and fields both inside and outside of the cylinder. One can show that accurate within a sign selection of the vector of angular velocity obtained field values for particular case of rotating hollow charged cylinder coincide with similar values [22] [23] .

From the view point of rotating RF the presence of electric field inside the cylinder should result in radial movement of the charge being at rest in IRF inside the cylinder cavity. However this is not correct.

It is clear from obtained solution from the IRF view point that inside the cylinder electric field is absent and relatively to magnetic field the test charge being at rest in IRF inside the cavity is motionless. So from the IRF view point there are no any forces acting on the test charge inside the rotating charged cylinder. The situation with the test charge is equivalent to the placing of this charge inside the solenoid when the charge is being at rest relatively the solenoid.

From the view point of the observer locating at the rotating cylinder the charge being at rest in IRF will move relatively NRF on the circle with radius r with the velocity inversely to the rotating disk. Now it is important to clear up how the radial component of external force from the side of electromagnetic field from NRF view point changes if from IRF view point it was equal to zero. In non-relativistic mechanics [24] the equation of motion of material point relatively uniformly rotating frame of reference has the form

(3.77)

where is the relative velocity; is the force acting on the particle from the side of electromagnetic field. If inside the cavity the particle is being at rest relatively IRF then. Substitution of last correlation to (3.77) results in the correlation

(3.78)

which is equivalent to the circumstance that the sum of the Coriolis force and the centrifugal one stipulates for the relative centripetal acceleration. The force from the side of electromagnetic field on the test particle in the cylinder cavity consists of the sum of the force from the side of electric field (3.59) and the force from the side of magnetic field (3.66). Let the test charge q being at rest in the cavity in IRF is positive and the cylinder is charged positively too. Then obviously that the force from the side of electric field is directed on the radius from the centre and the force from the side of magnetic field is directed on the radius to the centre. The summation forms

(3.79)

Thus, the absence of the particle radial motion is the invariant factor both from IRF and from NRF. We point out that the last formula is relativistic.

4. Comparison of Electromagnetic Fields in Möller’s NRF and in NRF in the Space of Constant Curvature. Discussion

Electrodynamic equations in NRF with specified structure outwardly do not differ from electrodynamic equations when the gravitational field is present [1] , where metric coefficients are determined from ( [16] , (2.18)).

(2.18)

The Maxwell equations for NRF with specified structure and Lorentz conditions will have the form [1]

(4.1)

So we present only simplest correlations on the basis of the concrete form of the metric ( [16] , (2.18)). For example we consider one of the “eternal problems” [25] concerning the field when the charge motion is uniformly accelerated. From (4.1) and metric ( [16] , (2.18)) we find the solution from Lorentz conditions

(4.2)

For the potential of the point charge trapped to the origin of NRF coordinates when the Lorentz conditions are satisfied the static Maxwell equations are reduced to the form

(4.3)

or after simplifications

(4.4)

We find the Solution (4.4) in the form

(4.5)

Whereupon equation for u will reduce to the form

(4.6)

and its solution will be

(4.7)

We point out though the space ( [16] , (2.18)) is Riemannian but its space section is Euclidian in which the radius-vector exists. It follows from the considered material that the solution of Equation (4.4) has the form

(4.8)

For electric intensity we have

(4.9)

where r is three-dimensional (Euclidian) distance from the origin of coordinates coinciding with the charge to the observation point; is the angle between the radius―vector and,.

For the convenience of the transformations between RF we rewrite the solutions in the tensor form. In accordance with (4.9) field tensor components differed from zero have the form

(4.10)

is the unit vector along r in three-dimensional space with the metric.

For space components of electromagnetic field tensor from (4.2) we have

(4.11)

This means that in NRF magnetic field is absent. As it is known [1] , tensor of pulse-energy of electromagnetic field in curvilinear coordinates can be presented in the form

(4.11a)

It follows from ( [16] , (2.18), (4.10), (4.11)) that the Pointing vector

(4.12)

that means the absence of the radiation in NRF. The transition to quasi-IRF is presented in accordance with the rules of the section 4, and it results in the law of motion from the correlations ( [16] , (3.5)) and ( [16] , (3.6)).

(3.5)

(3.6)

(4.13)

From (4.13) in accordance with the usual rules of tensor transformations we have

(4.14)

From whence we find

(4.15)

(4.16)

The transition to the standard coordinates is realized in accordance with the rule

(4.17)

(4.18)

where in accordance with ( [16] , (6.1))

(6.1)

we convert only t time coordinate expressing it via the T time of the Minkowski space and leaving constant space coordinates, i.e.. As a result we obtain

(4.19)

where is the time component of the metric tensor in standard coordinates ( [16] , (6.2)).

(6.2)

By means of tetrads ( [16] , (7.1))

(7.1)

we find tetrad components of the field tensor in standard coordinates

(4.20)

Considering the electromagnetic field tensor as correspondence invariant and identifying tetrad components of the field tensor in standard coordinates with affine components in IRF ( [16] , (2.4))

(2.4)

we obtain expressions for components of electromagnetic intensities in cylindrical coordinates in the form

(4.21)

(4.22)

where is the polar radius,. The value can be expressed via IRF coordinates by means of the law of motion ( [16] , (2.5)) or ( [16] , (3.9)) and the correlation ( [16] , (6.1))

(2.5)

(3.9)

and it has the form

is determined from the formula, where is determined by the expression in the brackets in. Calculation of magnetic field results in correlations:

(4.23)

where t is connected with the T time IRF by the formula ( [16] , (6.1)). To compare let us present the Born results [19] rewritten in our designations.

(4.24)

Let us carry out some preliminary analysis of obtained solution for the point charge field in the space-time of the constant curvature and compare this one with the Born solution. In particular, it follows from the obtained solution

(4.25)

From the Born solution a similar relation in accordance with (4.24) has the form

(4.26)

It follows from last correlation that. Only on this understanding the component of the Möller metric is positive.

Analysis of obtained results shows that for components of electric intensities and the expansion in a power series, , taking into account specified terms results in similar expansion obtained from the M. Born solution.

The problem concerning the charge radiation with uniformly accelerated motion is discussed. After the publishing of survey [25] in which the author considers that the “eternal problem” of the classic physics is closed, works [18] [26] - [31] appear, where the discussion is continued. For example, in [18] the presence of the radiation in NRF is connected with the existence possibility of negative value of metric tensor component, for the Möller metric this is equivalent to the transition to the complex plane for space variables and time. The transition from the Möller metric to the Whittaker metric does not change the problem, since the connection between two metrics is determined with the substitution of the Lagrange coordinate by other Lagrange coordinate z in accordance with the formula

which transforms the Möller metric ( [16] , (2.12))

(2.12)

into the Whittaker metric

(4.27)

component of metric ( [16] , (2.12)) is connected with similar component of the Whittaker metric by the correlation

and the demand of negativity in the Whittaker metric results in complexity of in the Möller metric.

On the other hand as it has been shown in [3] in the Möller metric the “horizon” exists, i.e. such NRF can be realized with bodies of finite dimensions along the movement direction. If in the initial moment the body was at rest and afterwards it began to move with uniform acceleration as a unit then initial dimensions of this body are restricted with the inequality. This inequality in Euler variables is equivalent to the correlation determining the permitted area of the determination of coordinate and time values in IRF occupied by the moving body. As shown in [18] , in analyzing the Born solution, when the last inequality is valid at the fixed T time moment fields do not form the wave zone and consequently the radiation is absent. It is this standpoint is presented in the known V. Pauli book [32] .

The demand [18] to extend the IRF space-time on the area of complex values of coordinates and time results in the forming of the wave zone outside of the “horizon”, from our standpoint the physical sense of this zone is very mistakable. In [26] - [31] the so-called invariant radiation criterion is considered, the sense of this criterion reduces to the division of electromagnetic field of moving charge on the “connected” and “free” parts. The full energy-pulse tensor of electromagnetic field decomposed on parts satisfies both in whole and separately to laws of conservation. Basing on the determination [30] the NRF, in which the Pointing vector in all points is equal to zero, is introduced. However, on the assumption of the accepted field decomposition into connected and radiated parts the vanishing of the Pointing vector does not mean the absence of the radiation in the NRF under consideration. In such NRF the energy flux of the connected field completely compensates the flux of the radiation energy. To our mind such division on the connected field and the radiation field is artificial. One can always divide the total zero into two or more nonzero parts, and the problem concerning the radiation of the charge making the hyperbolic motion remains open.

To our mind the reason of the paradox arising consists of following:

The particular solution of the Maxwell equations in the form of retarded potentials or the solution for the Lienard-Wiechert potentials in the case of the point charge in accordance proposes the presence of the radiation in the system. i.e. from the Lienard-Wiechert solution one can conclude: “The radiating charge moves with the acceleration”. Inverse statement: “The charge moving with the acceleration radiates” to our mind is not always valid. The search of the particular solution does not depend only on the form of the equation but on the physical situation. For example, solving the Maxwell equation outside of the single point charge being at rest we select the static solution instead of the wave one.

Let us consider the second example. In the constant gravitational field (in the Newton theory) the charge being at rest hangs on the thread. Other similar charge is hung at the rocket flying with the acceleration, which is equal to the earth one far off gravitating bodies. Forces of the thread tension in these cases are the same. As physical situations in each of these systems are equivalent, so solutions of the Maxwell equations should be equivalent. But solutions in the first system are obviously static, consequently solutions in the second system should be static too. The second system is the uniformly accelerated NRF. Thus, in the problem concerning the field of the charge moving hyperbolically our standpoint coincides with the M. Born, V. Pauli and V. Ginsburg standpoint, that the charge moving hyperbolically does not radiate sufficiently long and “on the contrary if two rectilinear uniform movements transform in each other by means of the hyperbolic motion then the radiation takes place” [25] [32] .

We propose the following criterion of the absence of the moving charge radiation (or the charge system radiation).

If the charge (or the charge system) is “frozen” into the moving rigid in the Born sense body and if for the observer in this NRF the Maxwell equations permit the stationary solution for the fields created with this charge (the charge system), then such charge (the charge system) does not radiate.

Formulated condition of radiation absence is equivalent to the constancy of electromagnetic field (i.e. its independence on NRF time) relatively to the Lagrange rigid co-moving NRF, when the charge world line (or the congruency of world lines of the charge system) belongs to the congruency of world lines of NRF basis particles. Our determination of the constancy of tensor field and connected condition of the radiation absence differs from similar determination [33] (where the field constancy is the existence of the permitted coordinate system, in which field components do not depend on the time coordinate in some field of space-time).

One can obtain the analytical criterion of the radiation absence from the stationary criterion considered above by the author in Section 3. The criterion is determined by Formula (3.6) or the vanishing of the generalized force of the radiation friction (3.8).

For one charge moving progressively, and the generalized force coincides with the usual radiation braking force [1] . If electromagnetic field in NRF is stationary then Condition (3.7) is met and that in accordance with Pauli [32] means the absence of the radiation.

The Born solution investigated above fulfills to the condition of the radiation absence (3.6) if the charge making the hyperbolic motion is “frozen” in the Möller NRF ( [16] , (2.12)), and the movement of the Möller basis is considered in Euler IRF coordinates. If the world line of the considered charge belongs to the congruency of world lines of Logunov system basis particles ( [16] , (2.7), [16] , (2.8))

(2.7)

(2.8)

then Maxwell equations in such system do not permit the stationary solution, since this system is not the relativistic rigid system. However, we point out that one can’t say from this fact that the uniformly accelerated charge in the Logunov system radiates! The stationarity criterion is not applied in non-rigid systems. If to the world line of the uniformly accelerated charge from the Logunov system one “mentally adds” the world lines of uncharged particles from the Möller system, then the charge from the standpoint of our criterion does not radiate. Another example: the rubber bundle is joined to the charge attached to the wall. Other end of the bundle moves arbitrarily. It is clear, that in RF connected with the bundle Maxwell equations for the considered charge have non-stationary solutions, however the radiation is absent.

The charge “frozen” to the uniformly accelerated NRF ( [16] , (2.18)) does not radiate, it follows from Formulas ( [16] , (3.7), [16] , (3.13))

(3.7)

(3.13)

and resulting correlations,. Substitution of these correlations to (3.6) reduces it to an identity. Thus, obtained Solutions (4.21 - 4.23) in the Riemannian space-time is the analogue of the Born solution in the Minkowski space. Unlike the Born solution obtained one has no the “horizon” behind which the wave zone forms [18] . So the radiation is absent on whole IRF space-time domain.

One can check up that except the hyperbolic motion the uniformly rotating disk satisfies to criteria (3.6), (3.7). The radius of the disk is, where is the angular velocity. As it has been shown in [18] in the rotating reference frame determined by usual method [1] the charge does not radiate if and it radiates, when.

In [34] the author constructed the relativistic rigid uniformly rotating reference frame realized in the Riemannian space-time. Obtained solution is valid at any r distance from the rotation axis and metric tensor component is always positive. The generalized force of the radiation friction calculated in such system (3.8) becomes zero for all disk points that in accordance with the accepted criterion means the radiation absence for the charge system or one charge (“frozen” in the disk) being at any distance from the disk centre.

5. Spreading of Electromagnetic Fields in the Space of the Constant Curvature. Doppler Effect

Let us consider the wave spreading at the uniformly accelerated NRF ( [35] , (2.6))

(2.6)

on the basis of the Maxwell equations written in three-dimensional form as for the case of the static gravitational field [1] outside of sources

(5.1)

Acting with the operator on vector equations we obtain

(5.2)

(5.3)

Equation for proved to be exactly similar for. Let us consider some partial solutions of Equations (5.2), (5.3). We will find solutions in the TEM wave form, directing along axis with unit vector, along axis with unit vector and considering that both vectors depend only on the time coordinate and on one space coordinate with the unit vector collinear to the acceleration.

Omitting intermediate calculations, we find equations for waves spreading in directions collinear to the acceleration

(5.4)

(5.5)

Here. To solve (5.4) we will consider the preliminary expression

(5.6)

Let us introduce a new function. Then one can represent the Expression (4.6) in the form

(5.7)

Supposing that the expression in the parentheses (5.7) is equal to zero we obtain the equation

the solution of which is

Thus, the Expression (5.7) is represented in the form

(5.8)

If at small x the equality p = x is satisfied, we obtain and Equation (5.4) is equivalent to

(5.9)

i.e. it is equivalent to usual wave equation. In accordance with the considered problem the Solution (5.4) has the form

(5.10)

where and are arbitrary functions. The solution for magnetic field H is obtained as similar (5.10). The phase velocity v from the found solution obtained by the differentiation with respect to of the constant phase at, forms, where

.

Thus, as well as in the static gravitational field [1] one can say that in respect to its influence on electromagnetic field inertia forces change dielectric constant and magnetic permeability of the medium in which waves propagate. But this resemblance is only formal, since for waves, propagating along the acceleration direction at, and the phase velocity increases with x, always remaining greater then light velocity in vacuum. At for wave spreading in the opposite direction, and the phase velocity decreases with the removing from the source, remaining always smaller then light velocity in vacuum. From classic representations on the basis of the Galilean velocity addition one can expect the inverse result, so the phase velocity determined as the derivative of coordinate with respect to the world time is not a “physical” one. One can obtain the same value of the phase velocity by equalization interval ( [16] , (2.18)) to zero at fixed and values that checks calculations carried out.

The value of the phase velocity measured in tetrads ( [16] , (8.1)) will be the physical value of it

(8.1)

of the NFR metric ( [16] , (2.18))

(2.18)

determined with the equality

which results in values for and for.

Equating interval ( [16] , (6.2)) to zero

(6.2)

or converting the phase in obtained solution from NRF to standard quasi-IRF coordinates we find by two ways the same result for the phase velocity of the electromagnetic wave spreading relatively quasi-IRF in coordinates and time of the Minkowski space.

(5.11)

where.

The tetrad components of the phase velocity relatively quasi-IRF having directly a physical sense are obtained from (5.11) using metric ( [16] , (6.2)) and tetrads ( [16] , (8.1))

(5.12)

Thus, it follows from the wave solution of the Maxwell equation in NRF that the phase velocity of the electromagnetic wave spreading measured in the tetrads ( [16] , (8.1)) of the NRF metric ( [16] , (2.18)) or quasi-IRF metric ( [16] , (6.2)) is constant and it is equal to the light velocity in vacuum. Analysis of Formula (5.11) shows that the phase velocity of the wave spreading in coordinates and time of the Minkowski space does not exceed the light velocity in vacuum, at T = 0 and the velocity, and at the phase velocity is minimum and it is equal to 0.931c.

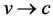
On the basis of the obtained Solution (5.10) we will make the calculation of the longitudinal Doppler effect when the source of plane monochromatic electromagnetic waves is located at the accelerated object at the origin of the Lagrange coordinate system, and at the time moment T = 0 Lagrange coordinates coincide with Euler coordinates. The expression for the eikonal and of plane waves from (5.10) in NRF ( [16] , (2.18)) has the form

(5.13)

(5.14)

and in quasi-IRF ( [16] , (3.7))

(3.7)

it is described by the formulas

(5.15)

(5.16)

where is the angular frequency.

The wave 4-vector determined as 4-gradient from the eikonal is the correspondence invariant, and for it tetrad components in quasi-IRF ( [16] , (6.2)) coincide with tetrad IRF components (which simultaneously are the affine components) ( [16] , (2.4))

(2.4)

Herewith ( [16] , (2.4)) and ( [16] , (6.2)) are specified in the general coordination. Using formulas ( [16] , (6.2)), ( [16] , (8.1)), (5.15), (5.16) and ( [16] , (3.10))

(3.10)

we find the expression for the frequency in IRF ( [16] , (2.4)) for the longitudinal Doppler effect when the source is approached to the receiver

, (5.17)

where v is the transmitter velocity determined from ( [16] , (3.10)).

If the source is removed from the receiver then the received frequency has the form

(5.18)

In Correlation (5.17) and in (5.18) y < 0. Analysis of Formulas (5.17) and (5.18) shows that the frequency change depends on two factors: inertial force potential characterized by the multiplier and the source velocity relatively the receiver that exactly corresponds to the STR Doppler effect [1] . First multiplier reduces the frequency when the source approaches to the receiver (red shift), and it increases the frequency when the source removes from the receiver (violet shift). The physics of this phenomenon is clear and it bases on the equivalence principle. One can rewrite Formulas (5.17) and (5.18) in Euler coordinates of the Minkowski space in the form

(5.19)

(5.20)

where the dependence of the source velocity v ( [16] , (3.10)) versus the time of the Minkowski space T is determined from ( [16] , (6.3)]

(6.3)

To compare these results we present expressions for the Doppler effect obtained from the solution of wave Maxwell equations in the Möller NRF ( [16] , (2.12)) (we point out that in ( [16] , (2.12)) T is the parameter numbering hyper surfaces orthogonal to world lines, but not a time of the Minkowski space. The solution of the problem results in

(5.21)

(5.22)

or going to Euler variables we obtain

(5.23)

(5.24)

where is the frequency received by the receiver at the point at the T time moment in Galilean coordinates of the Minkowski space for the source approaching to the observation point, and is the corresponding value for the source removing from the observation point. Because of the presence of the Möller metric “horizon” Formulas (5.23) and (5.24) are applied provided

.

Obviously if one selects the Lagrange coordinate that means, that at initial time the receiver and the transmitter coordinates coincided then Formulas (5.17) and (5.18) exactly coincide with the classic formulas for the SRT Doppler effect [12] . However, it only seems, as the velocities at the observation points from the Minkowski and Riemann space viewpoint will be different.

For example, we will continue the consideration of the problem presented in paragraph 6.6 [9] when astronauts fly by the nearest star of the Centaurus stellar system moving with uniform acceleration. From the standard viewpoint for the relativistic uniformly accelerated straight motion with the uniform acceleration at the intrinsic frame of reference [1] the rocket velocity at any instant is determined with the formula ( [9] , (6.84a))

(6.84a)

From our viewpoint the velocity value of the aircraft in accordance with ( [9] , (6.73a)) is

(6.73)

and ( [9] , (6.42))

(6.42)

at the standard coordinates has the form

(5.24a)

At the same time, the aircraft removes from the signal receiver located at the point.

In Figure 1 relative dimensionless velocities and depending on dimen-

sionless t time are presented. Here t is determined with the formula where T is the standard time of the Minkowski space.

One can see that from the viewpoint of two different theories the velocities of rocket overflying by the Proxima Centaurus will be different. In accordance with ( [9] , (6.84))

(6.84)

(6.82)

For our case that is observed in Figure 1.

By this reason, the identical frequency of electromagnetic waves radiated with the transmitting rocket device should differently receive with receivers at the spaceport (from the viewpoint of two different theories). Only the experiment can decide what theory is preferential.

In Figure 2 the frequency reduction calculated in accordance with the different theories is presented. is calculated according to classical Doppler’s Formula (4.18) at, where is substituted from the classical formula ( [9] , (6.84a)) instead of v.

is also calculated in accordance with Formula ( [9] , (8.41)).

(8.41)

where, however from ( [9] , (8.147a)) is substituted instead of v.

(8.147a)

When overflying by the nearest star the frequency received with the detector at the spaceport from the classical viewpoint should be 0.12 from the frequency radiated with the generator. In the case under consideration, the frequency received with the detector should be 0.02 from the radiated frequency.

When the velocity of removing source approaches to the speed of light the frequency received with the detector located at point tends to zero. It follows from ( [16] , (16.18)) and Figure 2.

Let us find the transformation of electromagnetic field of monochromatic plane wave from NRF of the Riemannian space ( [16] , (2.18)) to the IRF of the Minkowski space ( [16] , (2.4)) in accordance with the transition rules considered in previous section

. (2.4)

Let electric field of the wave, propagating on the acceleration direction in NRF ( [16] , (2.18)) (along axis), has the amplitude and it is directed along the axis, and magnetic field is directed along and it has amplitude. For the wave travelling from the source in opposite direction the electric field keeps the direction and the magnetic field changes the sign on opposite. Tensor of electromagnetic field has and components differed from zero. In accordance with [1] we find field tensor components for static gravitational fields in the form

(5.25)

(5.26)

where the phases in arguments are specified with Formulas (5.13), (5.14). The transition to quasi-IRF ( [16] , (3.7)) is realized in the ordinary way in accordance with the correlations

in which the dependence is specified with the law of motion ( [16] , (3.5), (3.6)).

(3.5)

(3.6)

Hereinafter by means of the time coordinate transformation ( [16] , (6.3)) we convert the tensor to quasi- IRF ( [16] , (6.2)) in standard coordinates, and then by means of tetrads ( [16] , (8.1)) we obtain physical components of the field tensor in the standard quasi-IRF, which in accordance with the proposed scheme coincide with field tensor components in IRF Galilean coordinates of the Minkowski space. Omitting intermediate calculations, we obtain finally

(5.27)

(5.28)

where are determined from (5.15), (5.16), and, are determined from Correlations (5.19) and (5.20).

To compare we present the solution of this problem in the Möller NRF transformed to the IRF of the Minkowski space. Omitting the calculations, we present the result

(5.29)

(5.30)

where and are determined from (5.23), (5.24), and the phases and are specified by formulas

(5.31)

(5.32)

The comparison shows that the solution of this problem by different ways (about the propagating of plane electromagnetic waves in the NRF and their receiving in the IRF) results in different results and only the experiment can clear up which calculation method is valid.

6. Conclusions

The main problems solved in this article are:

1) Reference frames

All NFR are divided into two classes:

a) NFR with specified law of motion.

b) NFR with specified structure.

It was shown that:

1) TheMöller transformation (the first class NFR) does not describe the transition into the globally uniformly accelerated NFR. Each Lagrangian particle moves with constant acceleration, but these accelerations are not equal each other. Therefore, the interpretation of the Möller transformation with the transition into the relativistic uniformly accelerated NFR is illegal.

2) The Logunov transformation (the first class NFR) describing the transition from NFR to the relativistic uniformly accelerated NFR in which each Lagrangian basis particle moves with constant acceleration results in the rigidity breaking. Thus, the globally uniformly accelerated Logunov system is not a relativistic rigid one.

Paradoxial result is obtained. Identical physical situation for all particles resulted in the motion of the particles relatively each other (the Logunov system). In order to make these particles be mutually immovable, one must apply different forces (the Möller system).

Thus, in the SR on the basis of the first class NRF, the logically elasticity theory [36] - [38] based on the lack of the deformations and tensions in the solid is not constructed, if this body moves freely in a uniform force field. Equal steady-state physical conditions for each medium particle result in non-stationary metric.

The description of rigid NFR in SR results in logical difficulties, which one can overcome by means of the going beyond the frames of flat space-time.

It follows directly from the obtained equations of structure.

2) On the basis of the structure equations, the theory of relativistic rigid uniformly accelerated NFR of the second class is constructed. This theory is realized in the Riemannian constant curvature space. When constructing NFR the approach is based on the obvious demand of the lack of the deformations and tensions in the solid in its translatory motion in the uniform force field. This results in the solution of the known Bell paradox. This paradox is on principle unsolvable in Minkowsky space.

As the NFR metric is the Riemannian one, then no transformations of coordinates including ones containing the time one cannot transform from IFR of Minkowski space to the NFR of the Riemannian space. It is impossible to create or obtain zero Riemann-Christoffel tensor using any transformations of coordinates. We obtain zero Riemannian tensor by means of the nonholonomic transformations from Minkowski space. However, one can divide this zero tensor into the parts from which one can eliminate nonzero standard Riemannian tensor.

Therefore, in interpretation of the measurements of physical values expressed by means of geometrical objects, the difficulties arise. These difficulties are partially got over by means of introduction of the “standard” coordinates, which coincide with the Galilean coordinates in Minkowski space. On the basis of “inoculating” coordinates of the flat space-time, we construct the NFR metrology in Riemannian space-time. That permitted to clarify the metric sense of measured physical values.

The field of a point charge being at rest in IFR is the Coulomb spherically symmetric one. It does not depend whether this charge is free or the sum of forces acting on the charge is equal to zero. On the other hand, the field of this charge moving uniformly accelerated in accordance with the classical electrodynamics for the NFR observer will be axially symmetric regardless of the NFR transition method.

Thus, identical physical situation in which the charges are (identical thread tension) results in the fields with different symmetry! The paradox is present. An attempt to solve it was undertaken in this article.

3) Exact static solution for the charge field in the uniformly accelerated NFR realized in the Riemannian space-time in aggregate with the “postulate of equivalent situations” permits in principle to find the space-time structure and determine the fields of charged arbitrary shape conductors. For positively charged bodies the “relativistic corrections” are small and usual electrostatics in Minkowski space is correct. For negatively charged conductors or ones located at external electric field, these corrections can be significant. The reason of this phenomenon is ascertained and the simplest experiments to corroborate or disprove the predicted effects are proposed in this article.

4) Electrodynamics in the 1st and 2nd class NFR. The stationarity criterion (the absence of radiation)

The examples of calculation of electromagnetic fields in uniformly accelerated NFR are considered. The criterion of radiation absence of a charge or a charge system connected with zero generalized force of radiative friction is formulated. It was shown, that the charge executing a hyperbolic motion does not radiate electromagnetic energy long enough. It consists with the M. Born, V. Pauli, V. Ginzburg viewpoint. Obtained solution in the Riemannian space-time proved to be an analog of the M. Born solution in Minkowski space. As opposed to the M. Born solution obtained one does not have a “horizon” beyond which the wave zone forms, therefore the radiation is absent over the whole area of IFR space-time.

In constructed [38] rigid uniformly revolving reference frame realized in the Riemannian space-time the criterion of the radiation absence is also satisfied for charged particles “trapped” into the rotating disk.

The problem about electromagnetic wave propagation in uniformly accelerated NFR was solved and the field transformation from NFR to IFR was considered. The calculation of the longitudinal Doppler effect and the calculation of this effect at the Möller NFR were carried out. The comparison showed different results, and only the experiment can ascertain which approach is legitimate.

Thus, the development of the unconventional approach to NFR jointly with the postulate of equivalent situations resulted in origin a new field of research and revision of some regulations of the classical field theory. Proposed model eliminated the basic contradiction between the stippling of the charged particles and their infinite proper energy. It appears that not only gravitational, but electromagnetic fields can bend space-time geometry.

Acknowledgements

The authors would like to thank the reviewers for their valuable comments that help in improving the work.

Cite this paper

Stanislav A. Podosenov,Jaykov Foukzon,Alexander Potapov,Elena Men’kova, (2016) Electrodynamics in Noninertial Reference Frames. Journal of Applied Mathematics and Physics,04,806-843. doi: 10.4236/jamp.2016.44091

References