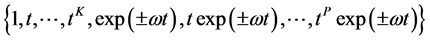Journal of Applied Mathematics and Physics
Vol.04 No.02(2016), Article ID:63837,8 pages
10.4236/jamp.2016.42043
Exponentially-Fitted 2-Step Simpson’s Method for Oscillatory/Periodic Problems
Ashiribo Senapon Wusu, Bosede Alfred Olufemi, Akanbi Moses Adebowale
Department of Mathematics, Lagos State University, Lagos, Nigeria

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 December 2015; accepted 23 February 2016; published 26 February 2016
ABSTRACT
Following a six-step flow chart, exponentially-fitted variant of the 2-step Simpson’s method suitable for solving ordinary differential equations with periodic/oscillatory behaviour is constructed. The qualitative properties of the constructed methods are also investigated. Numerical experiments on standard problems confirming the theoretical expectations regarding the constructed methods compared with other existing standard methods are also presented. Our results unify and improve the existing classical 2-step Simpson’s method.
Keywords:
Exponentially-Fitted, Simpson Method, Oscillatory, Periodic, ODE

1. Introduction
In this paper, we consider the first-order initial value problem of the form
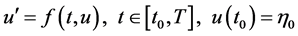 (1)
(1)
with oscillatory/periodic solution.
Several classical methods ( [1] - [5] ) for solving (1) have been derived. However, classical methods may not be well-suited for handling problems with pronounced periodic or oscillatory behaviour, because in order to accurately achieve this, a very small step size would be required with corresponding decrease in performance, especially in terms of efficiency. To overcome this barrier, classical methods have to be adapted in order to efficiently approach the oscillatory behaviour. The adaptation (which is called “exponential/trigonometric fitting”) is achieved by replacing some of the highest order monomials of the basis with exponentials or trigonometric (see [6] - [8] ). Numerical algorithms for solving problems whose solution exhibits a pronounced periodic or oscillatory behaviour has since the last decade gained a lot of attention. Such problems are often encountered in fields like mechanics, electronic, astrophysics, chemistry and engineering. The idea of using exponentially fitted formulae for differential equations was first proposed by Liniger and Willoughby [9] . Integration formulae containing free parameters were derived and these parameters were chosen so that a given function 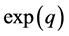 where q was real, satisfied the integration formulae exactly. This was tested on linear multistep method for
where q was real, satisfied the integration formulae exactly. This was tested on linear multistep method for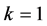 , however Jackson and Kenue [10] derived a fourth order exponentially fitted formulae based on a linear 2-step formula and were A-stable. Based on this idea, Cash [11] , in his own work, attempted using Multiderivative Linear Multistep Method (MLMM) with k = 1 in the second derivative formulae. Particular Runge-Kutta (RK) algorithms have been proposed by several authors [12] - [15] in order to solve this class of problems. Vanden Berghe et al. [16] [17] on the other hand, introduced other exponentially fitted RK (EFRK) methods which integrate exactly first-order systems whose solutions can
, however Jackson and Kenue [10] derived a fourth order exponentially fitted formulae based on a linear 2-step formula and were A-stable. Based on this idea, Cash [11] , in his own work, attempted using Multiderivative Linear Multistep Method (MLMM) with k = 1 in the second derivative formulae. Particular Runge-Kutta (RK) algorithms have been proposed by several authors [12] - [15] in order to solve this class of problems. Vanden Berghe et al. [16] [17] on the other hand, introduced other exponentially fitted RK (EFRK) methods which integrate exactly first-order systems whose solutions can
be expressed as linear combinations of functions of the form 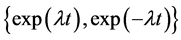 or
or .
.
Here, we analyze the construction and implementation of the exponentially-fitted variants of the 2-step Simpson method for solving problems of the form (1) which possess oscillatory/periodic solution, taking into account the six-step flow chart described by Ixaru and Vanden Berghe in [6] .
The main interest of this work is to modify the classical 2-step Simpson method for adaptation to oscillatory/ periodic problems.
2. Construction of Method
The classical 2-step Simpson method for solving (1) is given by
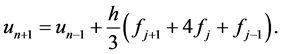 (2)
(2)
To begin the construction of the exponentially-fitted variants of (2), we rewrite (2) in a more general way as
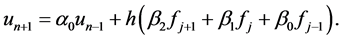 (3)
(3)
Following the six-step flow chart, the corresponding linear difference operator 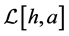 reads
reads
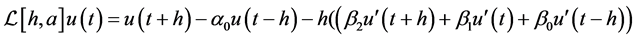
where 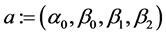
where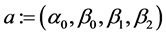 . Applying step II of the six-step procedure, the resulting system of equations is compatible when
. Applying step II of the six-step procedure, the resulting system of equations is compatible when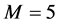 . Solving the resulting system, we have
. Solving the resulting system, we have
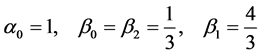 (4)
(4)
which are the coefficients of the classical method (2).
Applying step III, we find that
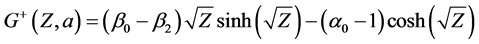 (5)
(5)
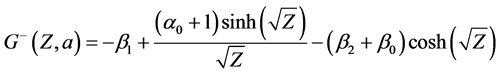 (6)
(6)
where 

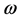



To implement step IV, consider the reference set of M functions:
with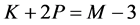

•
•
•
The coefficients of the method for each case are obtained by the implementation of step V as follows:
S1: 
S2:

S3:
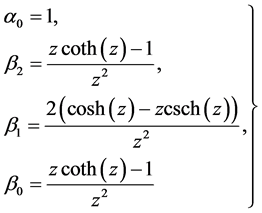
As expected, the exponentially fitted variants reduce to the the classical method as
3. Error Analysis: Local Truncation Error (lte)
The general expression of the leading term of the local truncation error (lte) for an exponentially fitted method with respect to the basis functions

takes the form (see [6] )

with K, P and M satisfying the condition
For the three methods constructed above, one finds the following results:
• S1:
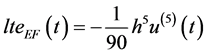
• S2:
• S3:
4. Existence and Uniqueness of Solution
The following theorem states conditions of 
Theorem 1. Let 






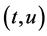



then if 



The requirement (12) is known as the Lipschitz Condition, and the constant 
This condition may be thought of as being intermediate between differentiability and continuity, in the sense that
• 
• Þ
• Þ
In particular, if 

where 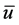

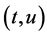



is chosen.
5. Contraction Mapping Theorem
In the sequel, we shall apply the following Contraction Mapping Theorem:
Theorem 2. (Contraction Mapping Theorem). Consider a set 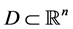

• D is closed (i.e., it contains all limit points of sequences in D)
•
• The mapping g is a contraction on D: There exists 
Then
• there exists a unique 
• for any


• 
and the a-posteriori error estimate
6. Application of the Contraction Mapping Theorem to LMM
If h is sufficiently small, implicit LMM methods also have unique solutions given h and




where
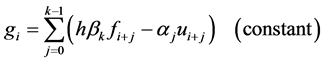
That is, we are looking for a fixed point of

If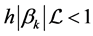


So by the Contraction Mapping Fixed Point Theorem, 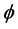


7. Convergence and Stability Analysis
Theorem 3 (Dahlquist Theorem) The necessary and sufficient conditions for a linear multistep method to be convergent are that it be consistent and zero-stable
Dahlquist theorem (3) holds also true for EF-based algorithms but, because their coefficients are no longer constants the concepts of consistency and stability have to be adapted.
Definition 4. An exponentially fitted method associated with the fitting space (9) is said to be of order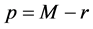
Since 
Definition 5. A linear s-step method is said to be weakly stable if there is more than one simple root of the polynomial equation 
To investigate the stability of (3), one applies the method to the test problems
From the above, one finds that
where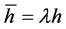

setting 

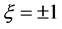
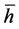
Definition 6. A region of stability is a region of the q--z plane, throughout which
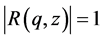

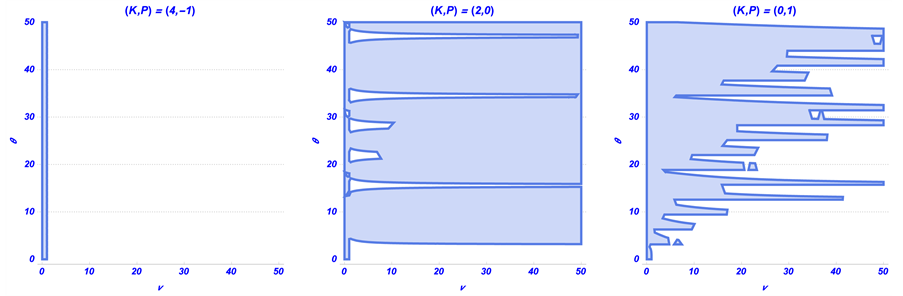
For each of the constructed methods, the region of stability is presented in Figure 1.
8. Numerical Results
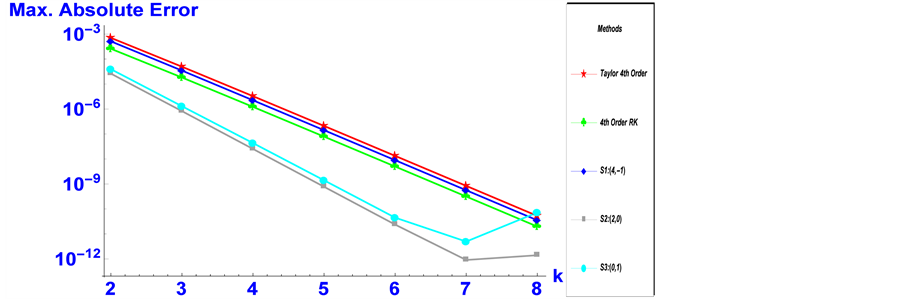
Numerical experiments confirming the theoretical expectations regarding the constructed methods are now performed. The constructed methods are applied to two test problems and the result obtained compared with the classical fourth-order Taylor method, explicit four stage fourth-order Runge-Kutta method and the classical 2-step Simpson method.
8.1. Problem 1
Consider the IVP: 

8.2. Problem 2
Consider the IVP: 


Figure 1. Truncated absolute stability regions of the constructed methods.
Figure 2. Maximum absolute errors for Problem 1 as a function of the step-size
Figure 3. Maximum absolute errors for Problem 1 as a function of the step-size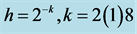

9. Conclusion
The exponentially-fitted versions of the classical 2-step Simpson method have been constructed and imple- mented in this paper. The stability and convergence properties of the constructed methods were also analysed. The results obtained from the numerical examples show that the theoretical expectations are meet (i.e. the expo- nentially-fitted variants of the classical 2-step Simpson method are suitable for solving periodic/oscillatory problems).
Acknowledgements
We thank the Editor and the referee for their comments.
Cite this paper
Ashiribo SenaponWusu,Bosede AlfredOlufemi,Akanbi MosesAdebowale, (2016) Exponentially-Fitted 2-Step Simpson’s Method for Oscillatory/Periodic Problems. Journal of Applied Mathematics and Physics,04,368-375. doi: 10.4236/jamp.2016.42043
References
- 1. Akanbi, M.A. (2011) On 3-Stage Geometric Explicit Runge-Kutta Method for Singular Autonomous Initial Value Problems in Ordinary Differential Equations. Computing, 92, 243-263.
- 2. Butcher, J.C. (2008) Numerical Methods for Ordinary Differential Equations. Wiley.
http://dx.doi.org/10.1002/9780470753767 - 3. Lambert, J.D. (1973) Computational Methods in ODEs. Wiley, New York.
- 4. Wusu, A.S. and Akanbi, M.A. (2013) A Three-Stage Multiderivative Explicit Runge-Kutta Method. American Journal of Computational Mathematics, 3, 121-126.
http://dx.doi.org/10.4236/ajcm.2013.32020 - 5. Wusu, A.S., Akanbi, M.A. and Fatimah, B.O. (2015) On the Derivation and Implementation of a Four Stage Harmonic Explicit Runge-Kutta Method. Applied Mathematics, 6, 694-699.
http://dx.doi.org/10.4236/am.2015.64064 - 6. Ixaru, L.G. and Vanden, B.G. (2004) Exponential Fitting Mathematics and Its Applications. Kluwer Academic Publishers, 568.
http://dx.doi.org/10.1007/978-1-4020-2100-8 - 7. Simos, T.E. (1998) An Exponentially-Fitted Runge-Kutta Method for the Numerical Integration of Initial-Value Problems with Periodic or Oscillating Solutions. Computer Physics Communications, 115, 1-8.
http://dx.doi.org/10.1016/S0010-4655(98)00088-5 - 8. Vanden, B.G. and Daele, M.V. (2006) Exponentially-Fitted Stomer/Verlet Methods. Journal of Numerical Analysis, Industrial and Applied Mathematics, 1, 241-255.
- 9. Liniger, W.S. and Willoughby, R.A. (1970) Efficient Integration Methods for Stiff System of ODEs. SIAM Journal on Numerical Analysis, 7, 47-65.
http://dx.doi.org/10.1137/0707002 - 10. Jackson, L.W. and Kenue, S.K. (1974) A Fourth Order Exponentially-Fitted Method. SIAM Journal on Numerical Analysis, 11, 965-978.
- 11. Cash, J.R. (1981) On Exponentially Fitting of Composite Multiderivative Linear Methods. SIAM Journal on Numerical Analysis, 18, 808-821.
http://dx.doi.org/10.1137/0718055 - 12. Avdelas, G., Simos, T.E. and Vigo-Aguiar, J. (2000) An Embedded Exponentially-Fitted Runge-Kutta Method for the Numerical Solution of the Schrödinger Equation and Related Periodic Initial-Value Problems. Computer Physics Communications, 131, 52-67.
http://dx.doi.org/10.1016/S0010-4655(00)00080-1 - 13. Bettis, D.G. (1979) Runge-Kutta Algorithms for Oscillatory Problems. Journal of Applied Mathematics and Physics (ZAMP), 30, 699-704.
http://dx.doi.org/10.1007/BF01590846 - 14. Coleman, J.P. and Duxbury, S.C. (2000) Mixed Collocation Methods for y” = (x;y). Journal of Computational and Applied Mathematics, 126, 47-75.
http://dx.doi.org/10.1016/S0377-0427(99)00340-4 - 15. Franco, J.M. (2002) An Embedded Pair of Exponentially Fitted Explicit Runge-Kutta Methods. Journal of Computational and Applied Mathematics, 149, 407-414.
http://dx.doi.org/10.1016/S0377-0427(02)00485-5 - 16. Vanden, B.G., Meyer, H.D., Daele, M.V. and Hecke, T.V. (1999) Exponentially-Fitted Explicit Runge-Kutta Methods. Computer Physics Communications, 123, 7-15.
http://dx.doi.org/10.1016/S0010-4655(99)00365-3 - 17. Vanden, B.G., Meyer, H.D., Daele, M.V. and Hecke, T.V. (2000) Exponentially-Fitted Explicit Runge-Kutta Methods. Computer Physics Communications, 125, 107-115.