Journal of Applied Mathematics and Physics
Vol.03 No.12(2015), Article ID:62332,5 pages
10.4236/jamp.2015.312193
The Nonideality Coefficient of Current-Voltage Characteristics for Asymmetric p-n-Junctions in a Microwave Field
Gafur Gulyamov1,2, Muhammadjon Gulomkodirovich Dadamirzaev1,2, Hasan Yusupovich Mavlyanov1,2
1Namangan Engineering Pedagogical Institute, Namangan, Uzbekistan
2Namangan State University, Namangan, Uzbekistan

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 October 2015; accepted 26 December 2015; published 29 December 2015
ABSTRACT
It is shown that the nonideality coefficient m actually depends on the electron temperature Te, and the hole temperature Th. We get more general expression for the nonideality coefficient, taking into account the concentration of electrons and holes, as well as their temperature, coefficient and diffusion length, the temperature of the phonons, the applied voltage, and the height of the potential barrier.
Keywords:
Hot Electrons, The Microwave Field, The Open Circuit Voltage, Short Circuit Current, Current-Voltage Characteristics of p-n-Junction, The Nonideality Coefficient

1. Introduction
The development occupies an important place in microelectronics, semiconductor devices; therefore it requires a deep study of the physical fundamentals of semiconductor devices based on p-n-junction and the impact of external and internal factors on the characteristics of these devices. The main characteristic of a semiconductor diode based on p-n junction is a voltage-current characteristic. The theory of an ideal p-n junction was developed by Shockley [1] . CVC real p-n-junction is different from the ideal. For CVC real p-n-junction from Shockley was introduced the nonideality coefficient [2] . External influences―pressure, light, temperature and other factors affect the nonideality coefficient of Current-Voltage Characteristics for p-n-junction.
In the works of S. P. Ashmontas [3] [4] , the effect of the heating of electrons was examined in the p-n-junc- tion under the influence of the microwave field by the nonideality coefficient.
The nonideality coefficient of CVC silicon p-n-junction in a microwave field was studied in the works of A. I. Veynger and others [5] [6] , where the abnormally high currents and electromotive force (EMF) had been observed.
However, the above-mentioned work is not considered dependence of the nonideality coefficient of the simultaneous heating of electrons and holes.
The aim of this work is to study the effect of heating of electrons and holes by a nonideality coefficient of CVC p-n-junction.
2. Theoretical Studies of Nonideality Coefficient of CVC Asymmetric p-n-Junction in a Microwave Field
The resulting expression of your total current passing through the diode consists of electron and hole currents and is defined as follows [7] [8] :
 (1)
(1)
where, ;
; 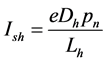 are the saturation currents for electrons and holes; j0: height of the potential barrier in the absence of an electromagnetic wave;
are the saturation currents for electrons and holes; j0: height of the potential barrier in the absence of an electromagnetic wave;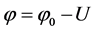 ; U: a voltage across the diode;
; U: a voltage across the diode;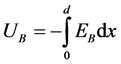 :
:
AC voltage of the incident wave created by the barrier diode; T is the temperature of the lattice; k: Boltzmann constant; Te and Th: the temperatures of electrons and holes; Eb―electric field of the wave; e is the charge of an electron; De and Dh―diffusion coefficients of electrons and holes, Le and Lh―their diffusion length; np and pn―the concentration of minority carriers.
Using the mean value theorem [9] :
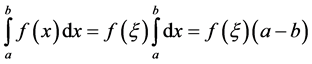
 ,
,
we received for the considered case

of formula (1) we have to CVC p-n-junction following expression:
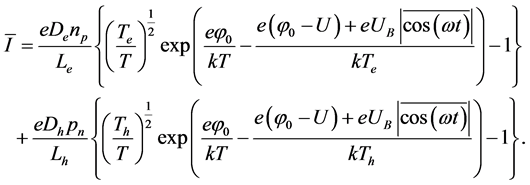 (2)
(2)
At low wave power (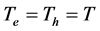 ; UB ≠ 0), when there is only outrage the potential barrier height, using the formula (2) obtain the CVC p-n-junction:
; UB ≠ 0), when there is only outrage the potential barrier height, using the formula (2) obtain the CVC p-n-junction:
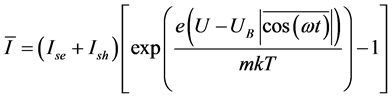 , (3)
, (3)
to take a logarithm of the expression (3), while taking into account the perturbation of the potential barrier height for the nonideality coefficient of current-voltage characteristics for p-n-junctions find the following formula:
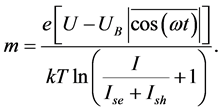 (4)
(4)
High power microwave energy heated electrons and holes have different temperatures. In the works of A. I. Vengera and other experiments were conducted in a highly asymmetrical p-n-junction, where 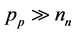 and
and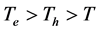 . However, under these conditions, the main share of the total current flowing through the p- n-junction, make hot holes [7] . Then the CVC p-n-junction consists of a second portion of the formula (2) and the first member can be neglected:
. However, under these conditions, the main share of the total current flowing through the p- n-junction, make hot holes [7] . Then the CVC p-n-junction consists of a second portion of the formula (2) and the first member can be neglected:
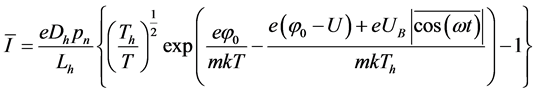 . (5)
. (5)
Hence, for the nonideality coefficient we obtain the following expression:

It is seen that the nonideality coefficient is mainly dependent on the temperature of the holes.
If
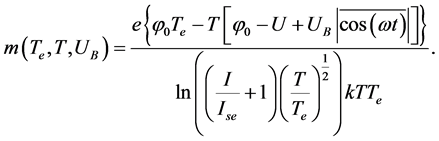
This expression depends mainly on electron temperature.
According to the analysis of the results shows that in the special case when
We get more general expression for the nonideality coefficient, which takes into account the asymmetry of concentration, temperature, diffusion coefficients, diffusion length for electrons and holes, the temperature of the phonons, and the applied voltage, the height of the potential barrier. Analyses show that the nonideality coefficient strongly influenced by the concentration of charge carriers and the temperature perturbation potential barrier height, which are consistent with experimental results. In addition to the analytical expressions ((4), (6), (7)) on the basis of formula (1) can be transcendental equation coefficient imperfection independent simultaneous heating of electrons and holes. In addition to the analytical expressions ((4), (6), (7)) on the basis of formula (1) we received a transcendental equation for the nonideality coefficient, which depends on the simultaneous heating of electrons and holes.
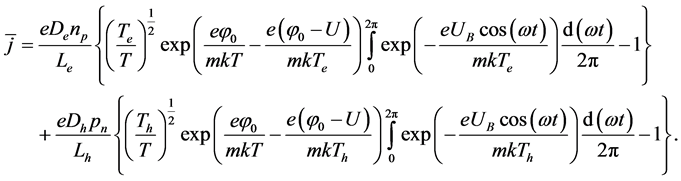
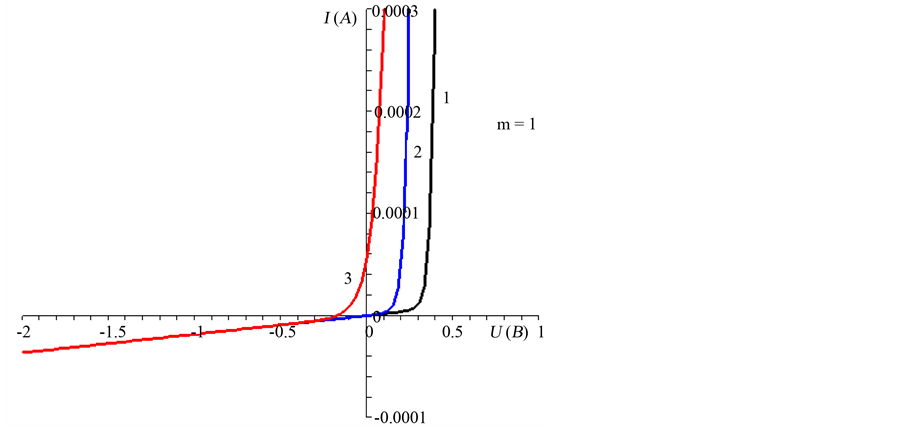
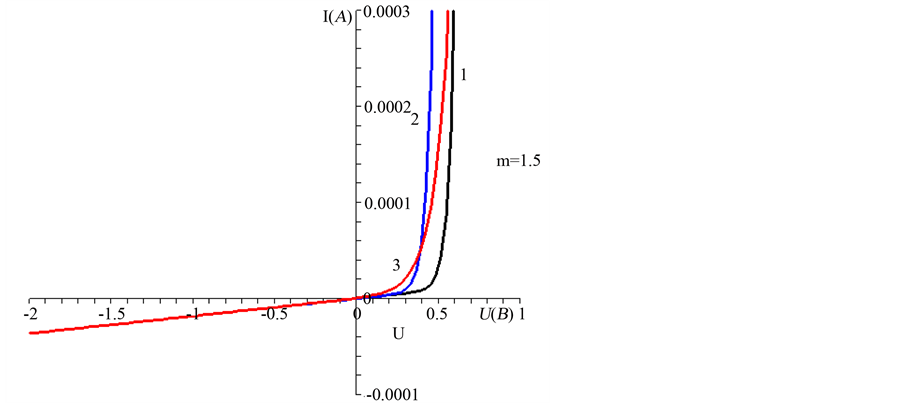
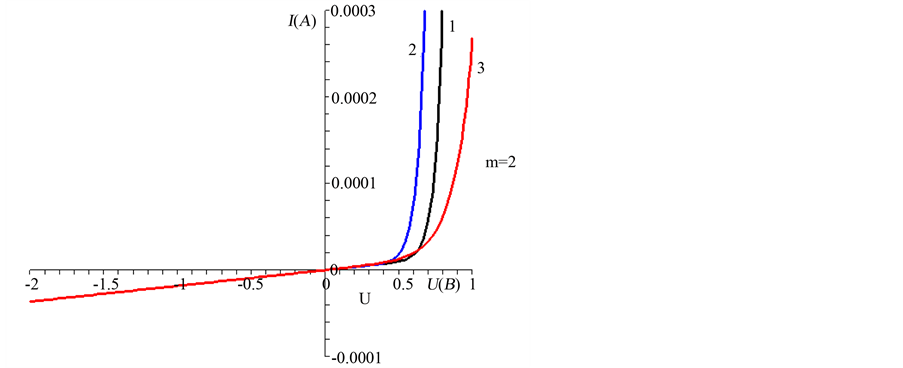
Using this formula, for different values of m we can construct CVC p-n-junction (Figures 1-3).
The graphs show that the nonideality coefficient is more sensitive to the microwave field and the current- voltage characteristics of p-n-junction is shifted to higher direct voltage with an increase in the nonideality coefficient.
Figure 1. CVC p-n-junction, provided: 1―without the microwave field, 2―at low microwave powers wave and 3―at high power microwave energy and m = 1.
Figure 2. CVC p-n-junction, provided: 1―without the microwave field, 2―at low microwave power wave, and 3―at high power micro-wave energy and m = 1.5.
Figure 3. CVC p-n-junction, provided: 1―without the microwave field, 2―at low microwave powers wave, and 3―at high power micro-wave energy and m = 2.
3. Conclusions
The results show that the nonideality coefficient m really depends on the electron temperature and the temperature of the holes.
With 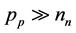
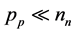
We get more general expression for the nonideality coefficient, taking into account the concentration of electrons and holes, as well as their temperature, diffusion coefficient and diffusion length, temperature phonons, applied voltage and indignation potential barrier height.
Cite this paper
GafurGulyamov,Muhammadjon Gulomkodirovich ,Dadamirzaev,Hasan YusupovichMavlyanov, (2015) The Nonideality Coefficient of Current-Voltage Characteristics for Asymmetric p-n-Junctions in a Microwave Field. Journal of Applied Mathematics and Physics,03,1679-1683. doi: 10.4236/jamp.2015.312193
References
- 1. Shockley, W. (1953) Theory of Electrical Semiconductors. Foreign Literature Publishing House, Moscow, 186 p.
- 2. Sah, C.T., Noyce, R.H. and Shockly, W. (1957) Carrier Generation and Recombination in p-n-Junctions and p-n-Junctions Characteristics. Proceedings of the IRE, 45, 1228-1243.
http://dx.doi.org/10.1109/JRPROC.1957.278528 - 3. Ashmontas, S.P., Olekas, A.P. and Shimulis, A.I. (1985) Effect of Warming up of the Charge Carriers in the Form of Current-Voltage Characteristics of p-n-Junction Germanium. Semiconductors, 29, 807-809.
- 4. Ashmontas, S.P., Olekas, A.P. and Shimulis, A.I. (1980) Temperature Anomalies Schottky Barrier Diodes Ni-n-Si. Lithuanian Physical Collection, 20, 39-46.
- 5. Veynger, A.I. and Sargsiyan, M.P. (1980) The Kinetics of the Thermopower Arising in the p-n-Junction with Heating Carrier. Semiconductors, 14, 2020-2027.
- 6. Ablyazimova, N.A., Veynger, A.I. and Pitanov, V.S. (1992) The Impact of a Strong Microwave Field in the Photovoltaic Properties of Silicon p-n-Junctions. Semiconductors, 26, 1041-1047.
- 7. Dadamirzaev, M.G. (2011) Heating of Charge Carriers and Rectification of Current in Asymmetrical p-n Junction in a Microwave Field. Semiconductors, 45, 288-291.
http://dx.doi.org/10.1134/S1063782611030092 - 8. Dadamirzaev, M.G. (2015) Influence of Deformation on CVC p-n-Junction in a Strong Microwave Field. Journal of Modern Physics, 6, 176-180.
http://dx.doi.org/10.4236/jmp.2015.62023 - 9. Smirnov, V.I. (1974) Course of Higher Mathematician. Vol. 1, Nauka, Moscow, 480 p.