Received 18 September 2015; accepted 24 November 2015; published 27 November 2015

ABSTRACT

We present the numerical method for solution of some linear and non-linear parabolic equation. Using idea [1] , we will present the explicit unconditional stable scheme which has no restriction on the step size ratio k/h² where k and h are step sizes for space and time respectively. We will also present numerical results to justify the present scheme.

Keywords:

Runge-Kutta Methods, Method of Lines, Difference Equation, Non-Linear PDE

1. Introduction

A number of difference schemes for solving partial difference equations have been proposed by using the idea of

methods of lines [2] [3] . The scheme is required the condition of step size ratio 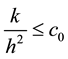for some constant,

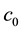where k and h are step sizes for space and time respectively. We [1] [4] -[6] have proposed some explicit scheme and overcome this problem. The problem considered in this paper is linear and nonlinear parabolic problem

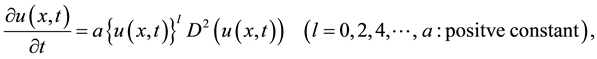(1.1)

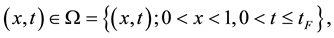
with the initial Dirichlet boundary condition

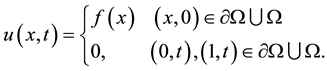(1.2)

where we set

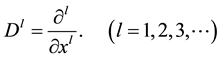(1.3)

We propose the difference approximation to (1.1) where the step size ratio is defined by

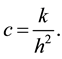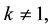(c is any positive constant) (1.4)

The outline of this paper is as follows. In §2, by using idea of methods of lines, we present the explicit difference approximation to (1.1). In §3 we study the truncation errors of our scheme. In §4 we study the convergence of the scheme with the condition (1.4) and we will show that our scheme converges to the true solution of (1.1). In §5 we study stability of the scheme, and we will show that our scheme is stable for any step size k and h with the condition (1.4). In §6 we show some numerical examples to justify our methods.

2. Difference Scheme

In the same way as in [1] , we will approximate (1.1) by replacing the derivative for space and time in the difference operator

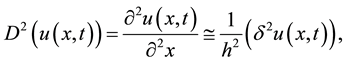
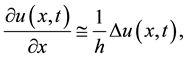(2.1)

where 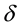is the central difference operator, 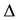forward difference operator. We denote the approximation to (1.1) at the mesh point

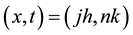
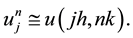
We set

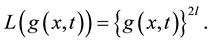(2.2)

We define the difference approximation to (1.1) by the following scheme.

If.

Then we set

(2.3)

If.

Then we set

(2.4)

where

(2.5)

The step size in (2.3), (2.4) is defined by

(2.6)

If we set

(2.7)

Then, from (2.3), (2.4), we have

(2.8)

3. Truncation Error

We define the truncation error of (2.8)

(3.1)

where, from the definition of (2.7), we have

(3.2)

By Taylor series expansions of the solution of (1.1), we have

(3.3)

From (3.3), we have

(3.4)

If we set

(3.5)

and

(3.6)

Then, from (3.4), we have the following result.

Theorem 1. The truncation error of the difference approximation (2.8) to (1.1) is given by

(3.7)

where

(3.8)

where and are defined by (3.5) and (3.6) respectively.

4. Convergence

In this section, we study the convergence of the scheme (2.8). We set the approximation error by

(4.1)

We use the abbreviation's

From (2.8), (3.7), (4.1), we have

(4.2)

with

(4.3)

From (2.5), we have

(4.4)

(4.5)

We set the initial conditions of (4.2)

(4.6)

Form (4.2), (4.4), (4.5), (4.6), we have

(4.7)

From (4.7), we have

(4.8)

with

(4.9)

(4.10)

We study the coefficients of (4.8) to.

Firstly we consider the case

(4.11)

We set

(4.12)

Then from (4.3), (4.12), we have

(4.13)

(4.14)

We have the equation

(4.15)

(4.16)

From (4.13), (4.14), (4.15), (4.16), we have

(4.17)

If we assume

(4.18)

Then we have

(4.19)

From (3.7), we have

(4.20)

with

(4.21)

From (4.20), we have

(4.22)

where is defined by (4.21).

We have from the condition (1.1)

(4.23)

From (4.17), (4.20), (4.23), we have

(4.24)

where is defined by (4.21) .

In the same way to (4.16), from (4.10), we have

(4.25)

From (3.8), we have

(4.26)

After some complicate computation, we have

(4.27)

with

From (4.27), we have

(4.28)

with

(4.29)

From (4.26), we have

(4.30)

with

From (4.30)

(4.31)

with

(4.32)

From (4.26), (4.28), (4.31), we have

(4.33)

From (4.25), we have

(4.34)

From (4.25), (4.33), (4.34), we have

(4.35)

where and are defined by (4.29) and (4.32) respectively.

From (4.20), we have

(4.36)

where is defined by (4.21).

From (4.8), (4.20) (4.24), (4.35), (4.36), we have

(4.37)

where and are defined by (4.21), (4.29) and (4.32) respectively.

We set the maximum norm of the function

(4.38)

Then, from (4.37), we have

(4.39)

From (4.39), we have

(4.40)

Finally we assume

(4.41)

Then, from (4.3), we have

(4.42)

From (4.9), (4.42), we have

(4.43)

In the same way to (4.14), we have

(4.44)

From (3.8), we have after some computation,

(4.45)

with

(4.46)

From (4.8), (4.20), (4.43), (4.44), (4.45), we have

(4.47)

where and are defined by (4.21) and (4.46) respectively.

Then, in the same way to (4.40), from (4.47), we have

(4.48)

We study l = 0. In the almost same way to (4.47), we have

(4.49)

where C₁ and C₄ are defined by (4.21) and (4.46) with l = 0 respectively.

From (4.49), we have

(4.50)

From (4.40), (4.48), (4.50), we have

Theorem 2. Suppose that for and, there exists positive numbers and such that

If the solution of (1.1) satisfies conditions (4.18). Then, the approximation generated by the scheme (2.8) converges to the solution of the differential Equation (1.1).

5. Stability

In this section, we study the stability of the numerical process (2.8) and define as follows.

Definition: The numerical processes is stable if there exists a positive constant such that

where denotes some norm and the constant is depends on initial value.

We prove that the scheme (2.8) are stable in mean of the von Neumann.

We set

Then, from (4.7), we have

(5.1)

From (5.1), we have

(5.2)

where and are defined by (4.9), (4.10) and (3.8) respectively.

If we assume (4.18) on the solution of (1.1), Then,in the same way to (4.31), (4.33), (4.45), we have

(5.3)

for some constant.

From (5.2), (5.3), we have the following result.

Lemma 1. If we assume the solution of (1.1) satisfies (4.18), Then there exists the constant such that

(5.4)

with (5.5)

where is defined by (5.3). From (2.8), we have

(5.6)

We set the maximum norm of the function

(5.7)

We have the inequality

(5.8)

From (1.1), we have

From (5.8), we have

(5.9)

From (2.8), we have

(5.10)

and

(5.11)

From (5.10), (5.11), we have

(5.12)

Firstly we consider

Then from (5.9) and (5.12), we have

(5.13)

with

(5.14)

where K, are defined by (4.19) and (5.5) respectively.

From (5.14), we have

(5.15)

Lastly, we consider

From (5.12), we have

(5.16)

Firstly, we consider the case.

Then from (5.16), we have

(5.17)

We have

(5.18)

From (5.10). (5.17), (5.18), we have

(5.19)

with

(5.20)

where K and are defined by (4.19) and (5.5) respectively.

If, Then we set

(5.21)

From (5.21), we have

(5.22)

If, Then we set

(5.23)

From (5.23), we have

(5.24)

From (5.22), (5.24), we set

(5.25)

where and are satisfy (5.21) and (5.23) respectively.

From (5.6), (5.19) and (5.25), we have

and we have the following result

(5.26)

From (5.26), we have

(5.27)

where is defined by (5.25).

Secondly, in the case, from (5.12), we have

(5.28)

From (5.28), we have

(5.29)

with

(5.30)

where K and are defined by (4.19)and (5.5) respectively.

In the same way to (5.26), we have

(5.31)

where is defined by (5.30).

From (5.15), (5.27), (5.31), we have

Theorem 3.

If the solution of (1.1) is analytic on the region then the difference approximation (2.8) to (1.1) are stable.

6. Numerical Example

Lastly, we study the numerical test in the following non-linear Equation .

(6.1)

and the initial and boundary problem given by,

(6.2)

Applying the difference Equation (2.8) to (6.1) with (6.2), we have the the numerical results in Table 1 and Figure 1, Figure 2.

Table 1. (x = 0/100, 2/100, 20/100, 50/100, 70/100, 98/100), (t = 0, 2/100, 10/100, 20/100, 50/100).

As we see in Figure 1, Figure 2, the initial data diffuses slowly. Here the interval [0,1] is divided into

with.

Cite this paper

MasaharuNakashima, (2015) Unconditionally Explicit Stable Difference Schemes for Solving Some Linear and Non-Linear Parabolic Differential Equation. Journal of Applied Mathematics and Physics,03,1506-1521. doi: 10.4236/jamp.2015.311176

References