Journal of Applied Mathematics and Physics
Vol.03 No.05(2015), Article ID:56757,6 pages
10.4236/jamp.2015.35071
Fatigue Crack Analysis on the Bracket of Sanding Nozzle of CRH5 EMU Bogie
Delong Fu, Tao Zhang
Changchun Railway Vehicle Co., Ltd., Changchun, China
Email: dragonfdl@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 April 2015; accepted 24 May 2015; published 28 May 2015
ABSTRACT
Aiming at the fracture of the bracket of sanding nozzle of CRH5 EMU bogie, the fatigue strength analysis and modal analysis of the bracket were conducted according to En13749 and BS7608 standards, and the track excitation during the vehicle running was thoroughly analyzed. The cause leading to the fracture of the bracket was found and the bracket was redesigned.
Keywords:
Bracket of Sanding Nozzle, Model Analysis, Track Excitation

1. Introduction
With the development of high-speed train and the increase of the speed, some non-sustaining components of the bogie are affected by the wheel-rail excitation and the fatigue fractures thus often occur. Fatigue failure is not only related to the amplitude of vibration, but also associated with the vibration frequency. Once, cracks appear on the bracket of sanding nozzle of CRH5 EMU bogie after for 1,200,000 kilometers operation. Aiming at this fatigue fracture, the fatigue strength analysis and modal analysis of the bracket structure were conducted in this paper. Based on the modal theory, the natural vibration modes and track excitation were combined to be analyzed. The cause of the fatigue crack was found, which provided a basis for the improvement of subsequent structural design.
2. Introduction to the Structure of the Sander and Finite Element Model
A sander is mounted on the side sill end of the CRH5 EMU bogie, as shown in Figures 1(a)-(b). The sanding device is fixed on the side sill by bolts, and the nozzle bracket is connected to the sander; the baffle is fixed on the end of the side beam; the baffle, the nozzle bracket, the heating box and the nozzle are connected by bolts.


Figure 1. (a) Sander unit. (b) 3D model of sander.
The cracks occurred at the welding end of the rib plate, as shown in Figure 2.
In the finite element analysis, the sander was discretized by shell elements. The bolts connection was modeled using the bond constraints. The model totally consisted of 19,862 elements and 17,313 nodes. The hose and the bolts were ignored in the model. The joint of components and sander structure is considered as fixed constraint and the FEM model is shown in Figure 3.
3. Model Analysis
The sander is mounted on the end of bogie side beam, which would undertake complex loading condition in the process of train’s running. In addition, the sander will vibrate under the excitation of trail-wheel interaction due to its complex structure. Therefore, modal analysis on the whole sander system should be carried out, thereby the natural frequency range and the main vibration modes of the sander structure can be understood clearly so as to find the critical weak links sensitive to stress and the cause of cracks, providing the basis for structural improvement.
The results of modal analysis of the whole sander are shown in Figure 4. The first-order natural frequency is only 47.8 Hz, corresponding to the axial vibration of the connection region of nozzle bracket with the lower part of the sander and producing a relatively large stress. Taking into account the additional mass of sand-spurting hose and control cable connected to the sander bracket, and an elastic suspension support, the first-order natural frequency of the structure should be even lower. Based on experience, the first-order natural frequency is comparatively low.
Figure 2. Crack on the nozzle bracket.
Figure 3. FEA model of sander.
4. Strength Analysis
The whole sander is installed on the end of the bracket frame. According to the En13749 [1] standard, the exceptional acceleration loads which caused by the additional mass and attached to the bogie frame end are vertical ±6 g and lateral ±2 g respectively; the normal acceleration loads are vertical ±3 g and lateral ±1 g respectively. Under the combined action of vertical 3 g and lateral 1 g acceleration loads, the movement of nozzle bracket is a longitudinal swing, and the principal stress contour is shown in Figure 5. At the rib plate welding end of nozzle bracket inner side, there is an obvious stress concentration; and through interpolation calculation, the maximum stress at weld toe is about 15.7 Mpa.
5. Analysis of Wheel-Rail Excitation
When the vehicle is running, the wheel-rail interaction produces an excitation on the vehicle system. According to the test data [2] , the irregularities of high speed railway is very obvious, the high-frequency part of the wavelength is located in 1.4 m, 2.8 m, 6.5 m, etc. Among them, 2.8 m is close to the wheel circumference, so this frequency primarily reflects the wheel’s dynamic unbalance; 1.4 m is half the wheel circumfe-
Figure 4. First mode of sander.
Figure 5. The principal stress contour of nozzle bracket.
rence, it is the reflection of wheel’s ellipticity; 6.5 m is the length of track plate, so the frequency is caused by the forced vibration of track slab. In consideration of the wheel diameter 890 mm, when the train runs at a speed of 200 km/h, the corresponding excitation frequency is 40 Hz, 20 Hz and 8.55 Hz respectively; when the train is running at a speed of 250 km/h, the excitation frequency is 49.6 Hz, 24.8 Hz and 10.68 Hz respectively.
So, no matter whether the train runs at 200 km/h or 250 km/h, the wheel-rail excitation frequencies are all close to the natural frequencies of the sand. The wheel-rail excitation is a kind of forced vibration input, assuming the displacement of the bracket is 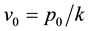 under the acceleration load
under the acceleration load  and the displacement of nozzle bracket due to the excitation of wheel-rail is v, according to the dynamic theory of [3] , the dynamic amplifying coefficient caused by the excitation is:
and the displacement of nozzle bracket due to the excitation of wheel-rail is v, according to the dynamic theory of [3] , the dynamic amplifying coefficient caused by the excitation is:

where  is the ratio of excitation frequency to structural natural frequency;
is the ratio of excitation frequency to structural natural frequency; 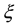 is the ratio of
is the ratio of
structural damping to critical damping, namely, 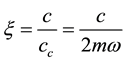 , usually
, usually .
.
Suppose train’s running speed is 200 km/h, means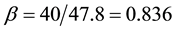 , then
, then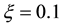 , and the amplifying
, and the amplifying
coefficient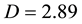 . Also
. Also
under the excitation of this frequency, the stress will be 2.89 times as much as the normal value in stiffened plate.
At the same time, the vibration acceleration is the two-order derivative of displacement, 
6. Fatigue Analysis
According to the BS7608 standard in [4] , in the welding structure similar to the stiffener, it is easy to produce cracks at the weld toe, and the weld type and failure are shown in Figure 6. This type of weld joint corresponding to F grade; when the corresponding number of cycles is 107, the stress range is 40 Mpa, as shown in Figure 7. Under the load of vertical 1 g and transverse 3 g, the stress at the weld toe position of rib plate welding end is about 15.7 Mpa. Due to an amplification effect of wheel-rail excitation, the stress range could reach up to 90.7 Mpa, far beyond the fatigue limit of F grade for welded joints. It is clear that, no matter whether the train runs at the speed of 250 km/h or 200 km/h, the fatigue strength of the sanding nozzle bracket cannot meet the requirements.
7. Improved Structure
It can be seen from the above analysis that the wheel-rail excitation frequency is close to the first-order natural frequency of sander. When the train is running, the first-order mode can be easily excited, resulting in abnormal vibration on the nozzle bracket and making the stress at the end of the internal welding rib plate exceed the fatigue limit. Based on this, we optimized the design of the sanding nozzle structure, aiming to increase the first-order natural frequency of the nozzle seat, or trying to avoid the stress concentration at the rib plate welding end of nozzle bracket inner side. The improved structure is shown in Figure 8. Its main structure remained unchanged but the installation base of the sander was widened in order to adapt to the new structure of stiffened welding plate. And the stiffened plate was extended to the baffle and the sander installation base; a piece of small rib plate was added to the middle part of the baffle to increase the baffle plate bending strength; the diameter of the holes in the sanding nozzle bracket and sander installation base were reduced from 70 mm to 50 mm. This improved structure has operated for 2,000,000 km running totally without any problems.
8. Conclusion
This paper used a method combining dynamic analysis with fatigue strength to conduct an in-depth study on the bogie sanding nozzle bracket structure, which took into account the intrinsic vibration mode of structure and rail
Figure 6. Welding class.
Figure 7. Designed S-N curve in BS7608.
Figure 8. Improved structure of the support bracket.
track excitation, then the reason that caused fatigue damage on the sanding nozzle bracket was found. On the basis of above analyses, the nozzle bracket structure was redesigned. The fatigue strength design method based on structural modal analysis has important theoretical significance and engineering value for the structural design of non-sustaining bogie components.
References
- En13749 (2005) Railway Applications-Wheelsets and Bogies-Method of Specifying Structural Requirements of Bogie Frames.
- Zhang S.G. (2009) Study on the Design Method of High Speed Train. China Railway Publishing House, Beijing.
- Clough, R. and Penzien, J. (2006) Dynamics of Structures. Chinese Edition, Higher Education Press, Beijing.
- BSI (1993) BS7608: Code of Practice for Fatigue Design and Assessment of Steel Structures. British Standards Institution, London.








