Theoretical Economics Letters
Vol.08 No.14(2018), Article ID:88006,19 pages
10.4236/tel.2018.814191
Improving the Forecast Accuracy of Oil-Stock Nexus in GCC Countries
Onuoha Ikwor Nnachi
Emerald Energy Institute, University of Port Harcourt, Port Harcourt, Nigeria

Copyright © 2018 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 3, 2018; Accepted: October 22, 2018; Published: October 25, 2018
ABSTRACT
This paper renders new insights into the predictability of GCC stock returns using crude oil prices using the approach of [1] [2] that accounts for salient features of the predictor. The results show superior performance of the oil-based stock model over time-series models (namely, AR, MA, ARMA, and ARFIMA) for both in-sample and out-of-sample forecasts. The results are robust to different oil price series (Brent and WTI prices) and forecast horizons (30 and 60 days).
Keywords:
Oil Price, Stock Price, Forecast Evaluation, GCC Countries

1. Introduction
There is an increasing evidence of improved stock return predictability using oil price [3] [4] . However, all the known studies are limited to the net-oil importing countries particularly the US while there is none specifically for individual net-oil exporting countries. The only exception is the [5] paper which involves panel data. Other related studies on net-oil exporting countries are limited to in-sample predictability which cannot be generalized for the out-of-sample period [6] [7] [8] . This is the motivation for this study.
Thus, the present study contributes to the literature in the following ways. First, it evaluates both the in-sample and out-of-sample forecast performance of oil-based stock model relative to time series models. Second, it accounts for some important features of oil price which may have implications on its forecast performance. Consequently, the approach of [1] [2] , which accommodates salient features such as endogeneity, persistence and conditional heteroscedasticity in the predictors of a series, is employed. This approach has been employed by a number of studies to examine the predictability of stock returns [3] [9] [10] [11] [12] [13] . The choice of GCC countries in this study is deliberate. Unlike other oil-exporting nations, these countries share similar characteristics given the increasing economic integration among them and therefore, a meaningful comparative analysis can be rendered. However, we prefer country-specific analyses to the panel data analyses in order to carefully develop a predictive model for oil-stock nexus for each country which can be subsequently adopted for policy analyses by the respective countries. Doing same for panel data may diminish the policy relevance of the results for the individual countries involved.
Following this section, the rest of the paper is structured as follows. The next section presents the predictive model for estimation and the underlying forecasting procedures as well as data scope. Section three contains preliminary analyses of data features. Section four discusses the results while Section five concludes the paper.
2. Methodology and Data
2.1. Estimation Approach
The intention of the empirical analyses here is to isolate the contribution of oil price in the predictability of stock returns. Nonetheless, any endogeneity bias that may result from ignoring important covariates is captured implicitly in the estimation process following the approaches of Lewellen (2004) and Westerlund and Narayan (2015). We begin our methodology by specifying a bivariate single predictive model where crude oil price is hypothesized as a predictor of stock price:
(1)
where is the log of stock price for each of the six GCC countries including Bahrain, Kuwait, Oman, Qatar, Saudi Arabia, and the United Arab Emirate; and is the log of crude oil prices where Brent price and WTI price are used separately in the estimation process. Thus, we have two predictive models for each of the oil price series across the six GCC countries considered (details about the data utilized are provided in the section that follows). The is zero mean idiosyncratic error term on stock price and the coefficient measures the relative impact of crude oil prices on stock price and the underlying null hypothesis of no predictability is that .
In order to resolve any probable endogeneity bias resulting from the correlation between and as well as any potential persistence effect, we follow the approach of [14] and [1] [2] . The underlying predictive model that accounts for these effects can be specified as:
(2)
where the parameter is the bias adjusted OLS estimator of [14] which corrects for any persistence effect in the predictive model. The additional term corrects for any endogeneity bias resulting from the correlation between and . Accounting for endogeneity bias here is important since there could be several determinants of stock prices which are suppressed in Equation (1). Such omissions could introduce endogeneity bias resulting from probable correlations between and . To resolve the conditional heteroscedasticity effect, [1] [2] suggest pre-weighting all the data by and estimating the resulting equation with the Ordinary Least Squares (OLS). This modified OLS estimator is described as the Feasible Quasi GLS estimator in [1] [2] and it is technically computed as:
(3)
where is used in weighting all the data in Equation (2) and .
In addition, three forecast measures are used to evaluate the in-sample and out-of-sample forecasts: the root mean square error (also called the mean square error), the [15] (C-T hereafter) test and the [16] test (D-M hereafter). The C-T test statistic is computed as , where and are the mean square error (MSE) obtained from the restricted and the unrestricted models, respectively. In the present case, our oil-based stock model in Equation (1) stands as the unrestricted model, whereas time-series models including AR (1), MA (1), ARMA (1, 1) and ARFIMA (1, d, 1), where d is the order of integration which is neither zero nor unity. A positive value of the statistic implies that our oil-based stock model is preferred to the time-series models in predicting stock prices; otherwise, it does not. By implication, a positive C-T statistic obtains from the fact that RMSE associated with our predictive model is less than that associated with the time-series models; but the reverse is the case for a negative C-T statistic. The D-M test is also used as a complementary test and it tests whether the difference between the forecast errors of two competing predictive models is statistically significant (or different from zero). While the D-M test is not suitable for small samples (which is not a concern given the large samples used for analyses), the test is however valid when the forecast errors are found to be non-Gaussian, nonzero mean, serially correlated, and contemporaneously correlated. A negative value and statistical significance of the D-M statistic at the conventional levels of 1%, 5% and 10% imply that our oil-based stock model significantly outperforms the time-series models; otherwise, it does not.
2.2. Data Description and Source
We focus attention on the stock markets of the six GCC countries, namely, Bahrain, Kuwait, Oman, Qatar, Saudi Arabia, and the United Arab Emirate so as to examine the sensitivity of their stock markets to changes in crude oil prices. We collect daily data on the two variables of interest, namely, stock prices of the six GCC countries and crude oil prices, comprising Brent price and West Texas Intermediate (WTI) price from various sources and over different time periods for most of the countries (see Table 1). All the data used for analyses were sourced from the Bloomberg terminal and the scope ranges from the period of 8th January, 1999 to 15th September, 2017. However, stock price data for Bahrain ranges between 11th July, 2004 and 10th September, 2017, and for the United Arab Emirate, stock price data are available between 6th October, 2001 and 2nd February, 2017. Thus, the analyses are conducted based on the available data for the individual countries.
3. Preliminary Analysis
3.1. Graphical Representation
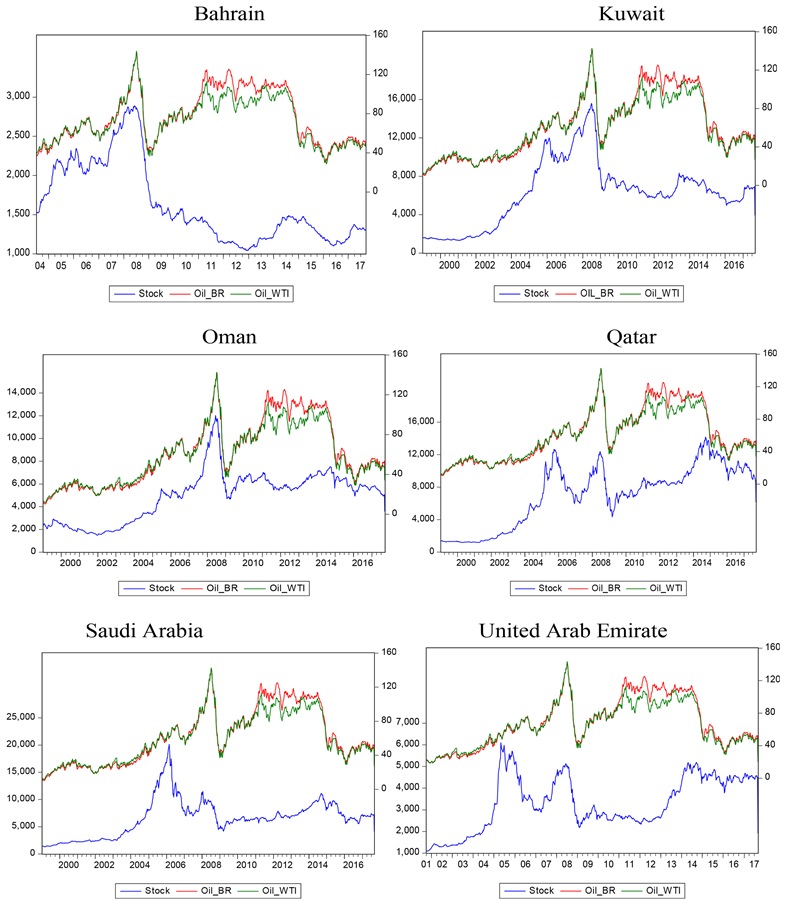
We represent the trends of stock prices and crude oil prices (Brent and WTI) for the six GCC countries in Figure 1. The direction of co-movements of stock prices and crude oil prices are mixed across the GCC countries. For instance, prior to the recent global financial crisis in September 2008, there exists a positive co-movement in both series in the cases of Bahrain and Kuwait, whereas stock prices and crude oil prices move in similar directions for the entire period in the case of Oman, Qatar, Saudi Arabia, and United Arab Emirate. In the case of Bahrain, most especially, the continuous drop in stock prices could partly be attributed to the fall-out of the Arab spring starting from 2010. Also, common to all is the outbreak of the 2008-09 global financial crisis which saw a shortfall in both stock and crude oil prices for the entire GCC countries. The uniform positive co-movement observed in the majority of the GCC countries reflects the close linkage between the world oil market and the GCC stock markets. The fact that oil prices lead stock prices, or stock prices lead oil prices remains an unresolved debate in the empirical literature.
It has been widely argued that the impact of oil price changes on stock market indices depends on whether a country is an oil exporter or an oil importer (see, for instance, [5] [17] [18] ). In an oil exporting country, increase in oil prices improves the trade balance, leading to a higher current account surplus and an
Table 1. Data description and scope.
Figure 1. Trends of stock prices and crude oil prices for the GCC countries.
improving net foreign asset position. At the same time, increase in oil prices tends to increase private disposable income in oil exporting countries. This in turn increases corporate profitability, raises domestic demand and stock prices thereby causing exchange rate to appreciate. In oil importing countries, the process works broadly in reverse: trade deficits are offset by weaker growth and overtime, real exchange rate depreciates and stock prices decrease [17] . The argument that oil price matters in stock pricing or not remains an empirical issue pursued later in this paper.
3.2. Descriptive Analysis
Table 2 presents the summary of descriptive statistics so as to observe the statistical features of stock prices and crude oil prices (Brent and WTI prices) for the GCC countries over their respective full sample periods. Both stock and crude prices are in their natural log forms. We observe that both Brent and WTI prices have approximately equal mean values. Also, stock price has the same average values in the cases of Qatar and Saudi Arabia, with Bahrain having the lowest average stock price in the group following Kuwait and Oman. In terms of standard deviation, Brent price is more volatile than the WTI price. Similarly, among the GCC countries, stock price in Bahrain is the least volatile while that in Qatar is the most volatile.
We also take account of other statistical features including skweness, kurtosis and Jarque-Bera statistic. In terms of skewness, we observe that the two oil price series (Brent and WTI prices) are negatively skewed, whereas all stock price indices, except that for Bahrain, are also negatively skewed. In terms of kurtosis, both stock and crude oil prices are largely platykurtic (for kurtosis values being less than 3.0). In addition, Jarque-Bera statistics indicate that all series (stock prices and crude oil prices) do not follow normal distribution across the GCC countries.
3.3. Autocorrelation and Heteroscedasticity Test Results
Here, we conduct autocorrelation and heteroscedasticity tests using Ljung-Box test Q-statistics and Autoregressive conditional heteroscedasticity lagrangian multiplier (ARCH-LM) test F-statistics, respectively (see Table 2) over the full sample period. We consider three different lag lengths (k) of 30, 60, and 90 for robustness. With respect to the predictors (crude oil prices), our results show the presence of significant serial dependence and conditional heterosedasticity at both lower and higher orders. Results are however mixed in the case of stock prices. Stock prices in the GCC countries except the United Arab Emirate suffer from serial correlation at both lower and higher orders. Generally, GCC stock prices except Bahrain’s and Qatar’s, fail to exhibit conditional heteroscedasticity at both lower and higher orders.
3.4. Persistence and Endogeneity Test Results
Premised on the fact that the rejection of the null hypothesis of a unit root for the predictors, which are crude oil prices (Brent and WTI prices) in our own case, is not a sufficient condition to assume the absence of persistence, we further test for persistence and endogeneity in the predictors (see Table 3) over the full sample period. The persistence test has the null hypothesis of no persistence
Table 2. Descriptive statistics.
Note: , , and are respectively, the natural logs of Brent price, WTI price, and stock price. Std. is standard deviation, Skw. is skewness, Kurt. is Kurtosis, and J-B stands for Jarque-Bera. For autocorrelation and heteroscedasticity tests, the reported values are the Ljung-Box test Q-statistics for the former and the ARCH-LM test F-statistics in the case of the latter. We consider three different lag lengths (k) of 30, 60, and 90 for robustness. The null hypothesis for the autocorrelation test is that there is no serial correlation, while the null for the ARCH-LM test is that there is no conditional heteroscedasticity. ***, ** and * imply the rejection of the null hypothesis in both cases at 1%, 5% and 10% levels of significance, respectively.
Table 3. Persistence and endogeneity test results for predictors.
Note: This table reports the endogeneity and persistence test results. Starting with the former, the test follows a three-step procedure: First, we run the following predictive regression model: where represents stock price and is the predictor variable (which are crude oil prices, in this case). In the second step, we follow [1] [2] and model the predictor variable as follows: and in the final step, the relationship between the error terms is captured using the following regression: . If the coefficient λ is statistically different from zero at any of the conventional chosen levels of significance such as ***, ** and * for 1%, 5% and 10%, respectively; then, the predictor variable is endogenous. For the latter however, the persistence test is conducted by regressing a first order autoregressive process for the predictor, for example: using OLS estimator. The first order autocorrelation coefficient (ρ) captures the persistence effect and is reported for each of the predictors. The null is that there is presence of persistence effect if ρ is statistically significant and the closer the value to one the higher the degree of persistence.
effect in the predictors. The coefficient of the AR (1) process was estimated for each predictor using OLS estimator and the results were found to be close or equal to one which is often the features of series with higher order of integration, thus, suggesting that the predictors (crude oil prices) contain persistent effects. We, however, observe that our predictors are largely exogenous.
4. Discussion of Results
In line with [3] [10] [11] [12] , we explore in-sample predictability of the theoretical model, which in this case is the oil-based stock model. The in-sample forecast is conducted using 75% of the full sample. The out-of-sample forecast, on the other hand, is based on three forecast horizons, namely, 30, 60, and 90 days. In the course of the forecast evaluation exercise, we also seek to validate the separate and opposing findings1 of [19] and [20] . In order to evaluate the forecast performance of our predictive model (that is, oil-based stock model) against time-series models (AR, MA, ARMA, and ARFIMA), we employ the root mean square error (RMSE), Campbell-Thompson (C-T) statistic, and Diebold-Mariano statistic. By implication, a positive C-T stat coupled with a negative D-M stat implies that the preferred model is our predictive model, and hence it is said to significantly outperform time-series models in predicting stock prices. However, a negative C-T stat coupled with a positive D-M stat is an indication that time-series models significantly outperforms our predictive model in predicting stock prices; hence, they constitute the preferred model. Similarly, we seek to investigate whether in-sample predictability and forecast evaluation tests are responsive to choice of oil price series (Brent and WTI prices) across the entire GCC countries. Predictability graphs are presented for both the oil-based stock model (using Brent price) and the time-series models for the GCC countries. Also, the predictability graphs of the oil-based stock model (using WTI price) for the GCC countries are presented in the Appendix.
4.1. In-Sample Predictability Results: Do Oil Prices Matter in Stock Pricing?
1 [19] concluded that GCC stock markets are information-efficient with regard to oil prices, and, by implication, oil prices do not tend to affect stock markets; hence, oil prices cannot be used as predictors for the GCC stock markets. [20] , however, confirmed that oil price shocks contain information for forecasting real stock return in the United States.
The predictability power of a potential economic predictor hinges on the statistical significance of the first-order autoregressive coefficient in the theoretical (predictive) model at the conventional levels of significance, namely, 1%, 5%, and 10%. It can be observed that irrespective of measures of oil price series (Brent and WTI prices), the null hypothesis of no predictability is rejected at 1% level of significance (see Table 4). We, therefore, conclude that crude oil prices play a significant role in predicting the behaviour of stock prices across the entire GCC countries. Our results confirm the findings of [21] , [3] and [20] that crude oil prices are good predictors of stock market indices. We also establish a positive linkage between crude oil prices and stock prices in support of the literature that suggests that the response of stock market returns to oil price shocks in a country greatly depends on the country’s net position in crude oil market and on the driving forces of oil price shocks [22] . It is crystal clear that the GCC countries account for 40% of world oil exports [23] ; with Saudi Arabian stock market showing the highest level of sensitivity to oil price
Table 4. In-sample predictability of stock indices using oil prices (Brent and WTI prices).
Note: The in-sample predictability in a bivariate model case is obtained by estimating the equation where δ denotes the coefficient on the predictor z, which in this case stands for crude oil prices. We employ both Brent and WTI prices as proxies for crude oil prices. ***implies the rejection of the null hypothesis of no predictability at 1% level of significance. The values in parentheses are the standard errors associated with the first-order autoregressive coefficients in our predictive model. Here, we consider 75% of the full sample data.
Fluctuations (see Table 4). Similarly, the literature on oil-stock nexus indicates that the stock markets of net-exporting countries can benefit from higher revenues and wealth arising from increasing crude oil prices, and vice versa [5] [17] [24] [25] .
4.2. Forecast Evaluation: Can Oil-Based Stock Model Beat Time Series Models?
We further compare the in-sample and out-of-sample forecast performance of our oil-based stock model with four time-series models including AR, MA, ARMA, and ARFIMA using the RMSE, the C-T and the D-M statistics (see Tables 5-10). Generally, we observe that our predictive model, which in this case is the oil-based stock model, significantly outperforms all the four time series models both in-sample and out-of-sample. The result is also robust to the choice of oil price series (Brent and WTI prices) and the choice of time-series models used as benchmark. This result supports the previous findings2 of [3] , and [5] . That our predictive model (oil-based stock model) predicts stock prices better than time-series models can do is reflected in the predictability graphs associated with both models (Compare Figure 2 and Figure 3, and refer to the Appendix for the predictability graphs using WTI price, see Figure A1). Following is a comparison of forecast performance between the oil-based stock model and each of the time-series models.
4.2.1. Oil-Based Stock Model versus AR Model
2 [3] established the superior performance of oil-price based predictive model over their benchmark model, which they called the constant returns model, in predicting stock returns out-of-sample for the US economy.
From the second to fourth columns of Table 7 and Table 8, we observe that C-T
Table 5. In-sample and out-of-sample forecast evaluation of oil-based stock models (RMSE).
Note: Capturing 75% of the full sample, we evaluate the in-sample and out-of-sample forecast performance (using 30 and 60 days as the forecast horizons) of our predictive model, which in this case is the oil-based stock model (using Brent and WTI prices) with the aid of root mean square error (RMSE). The smaller the root mean square error (RMSE), the greater the predictive power of a model and vice versa.
Table 6. In-sample and out-of-sample forecast evaluation of time-series models (RMSE).
*AR stands for autoregressive process/model; **MA for moving average process/model; ***ARMA for autoregressive moving average process/model, and ****ARFIMA for fractionally integrated autoregressive moving average process/model. Capturing 75% of the full sample, we evaluate the predictive power of the ARFIMA model both for the in-sample data and out-of-sample data cutting across the forecast horizons of 30 and 60 days using the root mean square error (RMSE). The smaller the root mean square error (RMSE), the greater the predictive power of a model and vice versa.
statistic is generally positive for the GCC countries except for Bahrain where the C-T stat is negative for the forecast horizon of 60 days. Since we are able to establish the predominance of positive C-T statistic, it can be concluded that our oil-based stock model is preferred to the AR model in predicting stock prices in the GCC countries. This result is generated from the fact that the RMSE associated with our predictive model is predominantly smaller than the RMSE associated with the AR model (compare Table 5 with the second to fourth columns of Table 6). A complementary conclusion is reached in the case of the D-M statistic which is predominantly negative and statistically significant at the 1% level (see the second to fourth columns of Table 9 and Table 10), with the implication that our oil-based stock model significantly outperforms the AR model
Table 7. In-sample and out-of-sample forecast evaluation of oil-based stock model (OSM) and time-series models using C-T test (Brent price case).
Note: The Campbell-Thompson (C-T) test statistics as used here compares the unrestricted model, which in this case is the oil-based stock model (using Brent price) with the time-series models (AR, MA, ARMA, and ARFIMA), which constitute the class of restricted models. Positive C-T stat implies that the oil-based stock model (using Brent price) is preferred to AR, MA, ARMA, and ARFIMA models in predicting stock prices using the in-sample data covering 75% of the full sample and the out-of-sample forecast horizons of 30 and 60 days. On the other hand, negative C-T stat implies that AR, MA, ARMA, and ARFIMA models are preferred to the oil-based stock model (using Brent price) in predicting stock prices using the in-sample data covering 75% of the full sample the out-of-sample forecast horizons of 30 and 60 days.
Table 8. In-sample and out-of-sample forecast evaluation of oil-based stock model (OSM) and Time-series models using C-T test (WTI price case).
Note: The Campbell-Thompson (C-T) test statistics as used here compares the unrestricted model, which in this case is the oil-based stock model (using WTI price) with the time-series models (AR, MA, ARMA, and ARFIMA), which constitute the class of restricted models. Positive C-T stat implies that the oil-based stock model (using WTI price) is preferred to AR, MA, ARMA, and ARFIMA models in predicting stock prices using the in-sample data covering 75% of the full sample and the out-of-sample forecast horizons of 30 and 60 days. On the other hand, negative C-T stat implies that AR, MA, ARMA, and ARFIMA models are preferred to the oil-based stock model (using WTI price) in predicting stock prices using the in-sample data covering 75% of the full sample the out-of-sample forecast horizons of 30 and 60 days.
in predicting stock prices across the GCC countries. Irrespective of choice of oil price series (Brent and WTI prices), we therefore establish the superior forecast performance of our predictive model over the AR model both in-sample and out-of-sample.
4.2.2. Oil-Based Stock Model versus MA Model
From the fifth to seventh columns of Table 7 and Table 8, we observe that C-T statistic is generally positive for the GCC countries except for Bahrain and the United Arab Emirate where the C-T stat is negative in both cases for the forecast
Table 9. In-sample and out-of-sample forecast evaluation of oil-based stock model (OSM) and time-series models using D-M test (Brent price case).
Note: The Diebold-Mariano (D-M) test statistic as used here compares the forecast errors of the unrestricted model, which in this case is the oil-based stock model (using Brent price) and the restricted model comprising the time-series models (AR, MA, ARMA, and ARFIMA). The negative and statistical significance at 1% (***), 5% (**) and 10% (*) implies that the oil-based stock model (using Brent price) significantly outperforms the AR, MA, ARMA, and ARFIMA models using in-sample data covering 75% of the full sample and out-of-sample forecast horizons of 30 and 60 days. However, the positive and statistical significance at 1% (***), 5% (**) and 10% (*) implies that the AR, MA, ARMA, and ARFIMA models significantly outperform the oil-based stock model (using Brent price) using in-sample data covering 75% of the full sample and out-of-sample forecast horizons of 30 and 60 days.
Table 10. In-sample and out-of-sample forecast evaluation of oil-based stock model (OSM) and time-series models using D-M test (WTI price case).
Note: The Diebold-Mariano (D-M) test statistic as used here compares the forecast errors of the unrestricted model, which in this case is the oil-based stock model (using WTI price) and the restricted model comprising the time-series models (AR, MA, ARMA, and ARFIMA). The negative and statistical significance at 1% (***), 5% (**) and 10% (*) implies that the oil-based stock model (using WTI price) significantly outperforms the AR, MA, ARMA, and ARFIMA models using in-sample data covering 75% of the full sample and out-of-sample forecast horizons of 30 and 60 days. However, the positive and statistical significance at 1% (***), 5% (**) and 10% (*) implies that the AR, MA, ARMA, and ARFIMA models significantly outperform the oil-based stock model (using WTI price) using in-sample data covering 75% of the full sample and out-of-sample forecast horizons of 30 and 60 days.
horizon of 60 days. Since we are able to establish the predominance of positive C-T statistic, it can be concluded that our oil-based stock model is preferred to the MA model in predicting stock prices in the GCC countries. This result obtains from the fact that the RMSE associated with our predictive model is predominantly smaller than the RMSE associated with the MA model (compare Table 5 with the fifth to seventh columns of Table 6). We reach a complementary conclusion in the case of the D-M statistic which is predominantly negative and statistically significant at the 1% level (see the fifth to seventh columns of
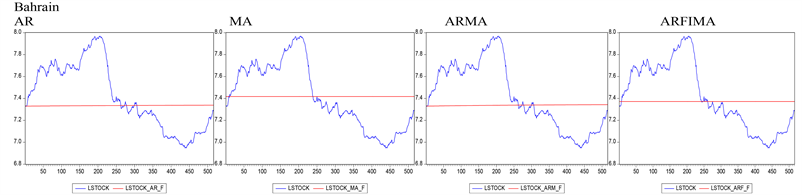
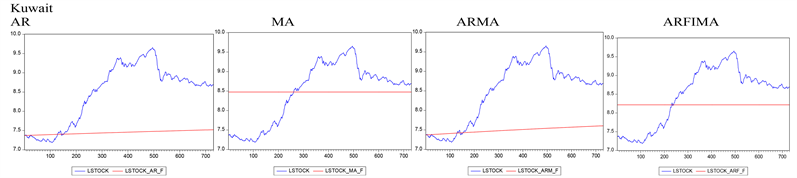
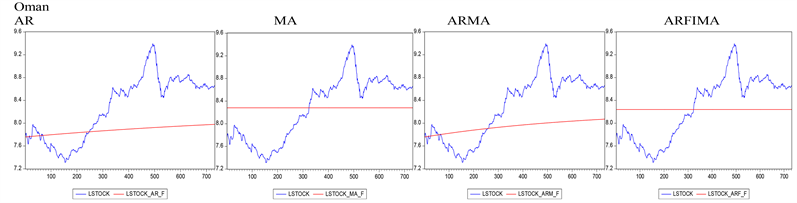
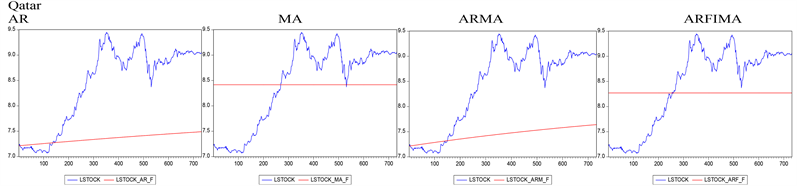

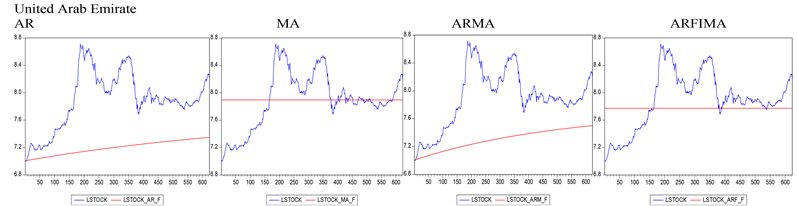
Figure 2. Predictability graphs for time series models.
Figure 3. Predictability graphs for oil-based stock models (using Brent price).
Table 9 and Table 10), with the implication that our oil-based stock model significantly outperforms the MA model in predicting stock prices across the GCC countries. Irrespective of choice of oil price series (Brent and WTI prices), we therefore establish the superior forecast performance of our predictive model over the MA model both in-sample and out-of-sample.
4.2.3. Oil-Based Stock Model versus ARMA Model
With regards to the eighth to tenth columns of Table 7 and Table 8, we observe that C-T statistic is generally positive for the GCC countries except in the case of Bahrain where the C-T stat is negative for the forecast horizon of 60 days. Since we are able to establish the predominance of positive C-T statistic, it can be concluded that our oil-based stock model is preferred to the ARMA model in predicting stock prices in the GCC countries. This result is informed by the fact that the RMSE associated with our predictive model is predominantly smaller than the RMSE associated with the ARMA model (compare Table 5 with the eighth to tenth columns of Table 6). A complementary conclusion is reached in the case of the D-M statistic which is predominantly negative and statistically significant at the 1% level (see the eighth to tenth columns of Table 9 and Table 10), with the implication that our oil-based stock model significantly outperforms the ARMA model in predicting stock prices across the GCC countries. Irrespective of choice of oil price series (Brent and WTI prices), we therefore establish the superior forecast performance of our predictive model over the ARMA model both in-sample and out-of-sample.
4.2.4. Oil-Based Stock Model versus ARFIMA Model
With respect to the eleventh to thirteenth columns of Table 7 and Table 8, we observe that C-T statistic is generally positive for the GCC countries except for Bahrain and the United Arab Emirate where the C-T stat is negative in both cases for the forecast horizon of 60 days. Since we are able to establish the predominance of positive C-T statistic, it can be concluded that our oil-based stock model is preferred to the ARFIMA model in predicting stock prices in the GCC countries. This result directly obtains from the fact that the RMSE associated with our predictive model is predominantly smaller than the RMSE associated with the ARFIMA model (compare Table 5 with the eleventh to thirteenth columns of Table 6). We reach a complementary conclusion based on the D-M statistic which is predominantly negative and statistically significant at the 1% level (see the eleventh to thirteenth columns of Table 9 and Table 10), with the implication that our oil-based stock model significantly outperforms the ARFIMA model in predicting stock prices across the GCC countries. Irrespective of choice of oil price series (Brent and WTI prices), we therefore establish the superior forecast performance of our predictive model over the ARFIMA model both in-sample and out-of-sample.
5. Conclusions
We offer new evidence of the predictability of stock prices using crude oil prices for the six GCC countries as a direct confrontation to the assertion of [19] that oil prices cannot be used as predictors for the GCC stock markets. Driven by the need to account for some salient features usually present in high frequency time-series data, we employ the estimator proposed by [14] and [1] [2] in order to account for possible persistence, endogeneity, serial correlation, and conditional heteroscedasticity effects in our predictors (which in this case, are crude oil prices). Our results show the presence of significant serial dependence, conditional heteroscedasticity and persistence effects in the predictors; while we at the same time establish the absence of endogeneity bias in the same predictors (that is, crude oil prices). Further, we are able to validate the hypothesis of significant in-sample predictability of stock prices using crude oil prices (Brent and WTI prices) across the six GCC countries to the contradiction of the previous findings of [19] . We also complement in-sample predictability results with superior out-of-sample forecast performance of our oil-based stock model over four strands of time-series models (namely, AR, MA, ARMA, and ARFIMA) using the forecast evaluation tools including the root mean square error (RMSE), Campbell-Thompson (C-T) statistic and Diebold-Mariano (D-M) statistic. Our results3 are robust to the choice of oil price series (Brent and WTI prices), the choice of benchmark time-series models (AR, MA, ARMA, and ARFIMA), and the choice of forecast horizons (30 and 60 days).
Meanwhile, quite a number of policy implications can be discerned from the various research findings in this paper. First, the information provided in this study as regards the ability of oil price to produce more accurate forecast for stock returns will be useful to financial analysts and investors who rely on such information for investment decisions. Secondly, policy makers will also find the results useful in terms of how much of information contained in the movements of oil price can be exploited by the stock market. This is particularly important during oil price crisis where policy makers are expected to implement policies to mitigate the negative spillover effects from oil to the stock market and other macroeconomic fundamentals. Notwithstanding the usefulness of the research findings of the study, a number of areas can still be explored to improve the paper and are therefore suggested for future research. The first area relates to the choice of countries; future research can conduct same for other countries particularly net oil importers and non-OPEC net oil exporters. The latter is also important to see if the results of the giant members of OPEC can be generalized for the non-members in terms of the predictive power of oil price in forecasting stock returns. The second area relates to other statistical properties underlying stock returns which are not captured in the current study. These properties include structural breaks and asymmetries. It will be an interesting exercise to see how the consideration of these properties will enhance the predictability of stock returns.
Conflicts of Interest
The author declares no conflicts of interest regarding the publication of this paper.
Cite this paper
Author 1, Author 2 and Author 3 (2018) Paper Title. Theoretical Economics Letters, 8, 3073-3091. https://doi.org/10.4236/tel.2018.814191
References
- 1. Westerlund, J. and Narayan, P.K. (2012) Does the Choice of Estimator Matter When Forecasting Returns? Journal of Banking and Finance, 36, 2632-2640. https://doi.org/10.1016/j.jbankfin.2012.06.005
- 2. Westerlund, J. and Narayan, P.K. (2015) Testing for Predictability in Conditionally Hetoroscedasticity Stock Returns. Journal of Financial Econometrics, 13, 342-375. https://doi.org/10.1093/jjfinec/nbu001
- 3. Narayan, P.K. and Gupta, R. (2015) Has Oil Price Predicted Stock Returns for over a Century? Energy Economics, 48, 18-23. https://doi.org/10.1016/j.eneco.2014.11.018
- 4. Salisu, A.A., Swaray, R. and Oloko, T.F. (2017) A Multi-Factor Predictive Model for Oil-US Stock Nexus with Persistence, Endogeneity and Conditional Heteroscedasticity Effects. Centre for Econometric and Allied Research, University of Ibadan Working Papers Series, CWPS 0024.
- 5. Salisu, A.A. and Isah, K.O. (2017) Revisiting the Oil Price and Stock Market Nexus: A Nonlinear Panel ARDL Approach. Economic Modelling, 66, 258-271. https://doi.org/10.1016/j.econmod.2017.07.010
- 6. Park, J. and Ratti, R.A. (2008) Oil Price Shocks and Stock Markets in the U.S. and 13 European Countries. Energy Economics, 30, 2587-2608. https://doi.org/10.1016/j.eneco.2008.04.003
- 7. Kilian, L., Rebucci, A. and Spatafora, N. (2009) Oil Shocks and External Balances. Journal of International Economics, 77, 181-194. https://doi.org/10.1016/j.jinteco.2009.01.001
- 8. Jung, H. and Park, C. (2011) Stock Market Reaction to Oil Price Shocks: A Comparison between a Nonoil-Exporting Economy and an Oil-Importing Economy. Journal of Economic Theory and Econometrics, 22, 1-29.
- 9. Bannigidadmath, D. and Narayan, P. (2015) Stock Return Predictability and Determinants of Predictability and Profits. Emerging Markets Review, 26, 153-173. https://doi.org/10.1016/j.ememar.2015.12.003
- 10. Narayan, P.K. and Bannigidadmath, D. (2015) Are Indian Stock Returns Predictable? Journal of Banking & Finance, 58, 506-531. https://doi.org/10.1016/j.jbankfin.2015.05.001
- 11. Narayan, P.K. and Bannigidadmath, D. (2017) Does Financial News Predict Stock Returns? New Evidence from Islamic and Non-Islamic Stocks. Pacific-Basin Finance Journal, 42, 24-45. https://doi.org/10.1016/j.pacfin.2015.12.009
- 12. Narayan, P.K., Phan, D.H.B., Sharma, S.S. and Westerlund, J. (2016) Are Islamic Stock Returns Predictable? A Global Perspective. Pacific-Basin Finance Journal, 40, 210-223. https://doi.org/10.1016/j.pacfin.2016.08.008
- 13. Devpura, N., Narayan, P.K. and Sharma, S.S. (2018) Is Stock Return Predictability Time-Varying? Journal of International Financial Markets, Institutions & Money, 52, 152-172. https://doi.org/10.1016/j.intfin.2017.06.001
- 14. Lewellen, J. (2004) Predicting Returns with Financial Ratios. Journal of Financial Economics, 74, 209-235. https://doi.org/10.1016/j.jfineco.2002.11.002
- 15. Campbell, J.Y. and Thompson, S.B. (2008) Viewpoint: Estimating the Equity Premium. Canadian Journal of Economics, 41, 1-21.
- 16. Diebold, F.X. and Mariano, R.S. (1995) Comparing Predictive Accuracy. Journal of Business and Economic Statistics, 13, 253-263.
- 17. Basher, S.A. and Sadorsky, P. (2006) Oil Price Risk and Emerging Stock Markets. Global Finance Journal, 17, 224-251. https://doi.org/10.1016/j.gfj.2006.04.001
- 18. Kayalar, D.E., Kucukozmen, C.C. and Selcuk-Kestel, A.S. (2016) The Impact of Crude Oil Prices on Financial Market Indicators: Copula Approach. Energy Economics, 61, 162-173. https://doi.org/10.1016/j.eneco.2016.11.016
- 19. Al Janabi, M.A.M., Hatemi-J, A. and Irandoust, M. (2010) An Empirical Investigation of the Informational Efficiency of the GCC Equity Markets: Evidence from Bootstrap Simulation. International Review of Financial Analysis, 19, 47-54. https://doi.org/10.1016/j.irfa.2009.11.002
- 20. Kang, W., Ratti, R.A. and Yoon, K.H. (2015) Time-Varying Effect of Oil Market Shocks on the Stock Market. Journal of Banking and Finance, 61, S150-S163. https://doi.org/10.1016/j.jbankfin.2015.08.027
- 21. Aloui, C., Nguyen, D.C. and Njeh, H. (2012) Assessing the Impacts of Oil Price Fluctuations on Stock Returns in Emerging Markets. Economic Modelling, 29, 2686-2695. https://doi.org/10.1016/j.econmod.2012.08.010
- 22. Wang, Y., Wu, C. and Yang, L. (2013) Oil Price Shocks and Stock Market Activities: Evidence from Oil-Importing and Oil-Exporting Countries. Journal of Comparative Economics, 41, 1220-1239. https://doi.org/10.1016/j.jce.2012.12.004
- 23. Ulussever, T. and Demirer, R. (2017) Investor Herds and Oil Prices Evidence in the Gulf Cooperation Council (GCC) Equity Markets. Central Bank Review, 17, 77-89. https://doi.org/10.1016/j.cbrev.2017.08.001
- 24. Arouri, M. and Rault, C. (2012) Oil Prices and Stock Markets in GCC Countries: Empirical Evidence from Panel Analysis. International Journal of Financial Economics, 17, 242-253. https://doi.org/10.1002/ijfe.443
- 25. Bouri, E. (2015) Oil Volatility Shocks and the Stock Markets of Oil-Importing MENA Economies: A Tale from the Financial Crisis. Energy Economics, 51, 590-598. https://doi.org/10.1016/j.eneco.2015.09.002
Appendix
Figure A1. Predictability graphs for oil-based stock models (WTI price).