Theoretical Economics Letters
Vol.08 No.05(2018), Article ID:83697,17 pages
10.4236/tel.2018.85065
Conviction Function? A New Decision Paradigm for Personal Financial Risk Management in the Face of Large Exogenous Shocks
Michael Cohen1, Munirul Nabin1, Sukanto Bhattacharya1, Kuldeep Kumar2
1Deakin Business School, Deakin University, Geelong, Australia
2Bond Business School, Bond University, Queensland, Australia

Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: January 31, 2018; Accepted: April 9, 2018; Published: April 12, 2018
ABSTRACT
This paper contributes to the limited-information literature on savings in a stochastic environment. In particular, it contributes techniques and concepts to the question of state verification (or filtering), by including learning about aggregate income shocks, based on signals. As a seminal contribution to the extant literature, a “conviction function” is introduced, which takes into account histories of past prediction errors in determining how rational agents internalize such information in taking personal investment decisions. For purpose of a more transparent illustration, a numerical rendition of the posited model is provided for five consecutive time periods. We also perform a series of Monte Carlo simulations to demonstrate how the posited approach could potentially outperform traditional forward-looking models in the presence of sudden large extraneous shocks reminiscent of the recent Global Financial Crisis.
Keywords:
Financial Risk, Stochastic Optimization, Conviction Function, Bayesian Learning, Large Shocks

1. Background and Motivation
In order to meet their retirement goals, savers need to react to adverse changes during the accumulation phase of retirement planning. One major cause of uncertainty during the accumulation phase is the stochastic nature of the returns on assets in a retirement portfolio. Thus many individuals, who had considered that their savings were adequate to meet their retirement needs prior to the global financial crisis (GFC), were rudely disappointed. In this article we examine the nature of an optimal retirement savings plan and the resilience of such a plan to large external shocks.
A retirement savings plan can in essence be reduced to a dynamic portfolio insurance strategy that actively allocates funds to a risky asset (or pool of risky assets) when the market is expected to move in a positive direction, and diverting funds to a low-risk asset when market returns are expected to decrease. However, a major shortcoming of such a plan is the “forward-looking” nature of these decisions. A purely prediction-dependent plan is fraught with non-negligible costs of prediction error. While auto-corrections for very small errors in prediction can be built into prediction-dependent models, the impact of large systemic shocks can jeopardize their predictive accuracy and render them unusable. Most significantly, if such shocks occur towards the end of the planning horizon (i.e. as an individual approaches retirement age) then the recovery time is often not adequate to allow the models to reach the target savings goal.
The motivation of this paper is two-fold. Firstly, we postulate a better retirement planning approach that incorporates both forward-looking as well as backward-looking techniques in dynamically determining the optimal path. We combine the standard dynamic programming approach that applies the Bellman principle with a Bayesian learning approach. This allows our posited approach to endogenously account for past errors in prediction. We present a numerical rendition of our posited dynamic optimization strategy for a five-period horizon via a rather large 32 × 32 event-action matrix to extricate the best possible outcome for each error in prediction made in the past periods. This illustrative method quickly becomes computationally intractable for large values of n, but n = 5 helps to adequately illustrate our case. A rational Bayesian learner should not be affected by his/her past performances as he/she has incorporated all possible match/mismatch between his/her signals and states; and updated his/her beliefs accordingly. However, in the real world the assumption of rationality may not hold as past performance may be considered one of the crucial factors of analyzing one’s investment decision, in particular, managing the risk portfolio. We therefore examine the case of using past performance as a tracking error and consider the implication for the Bayesian learner’s decision making process. We find that in the case when the past performances revealed a great number of mistakes, this leads the Bayesian learner into an unnecessarily conservative investment decision making process. However, the reverse is not true i.e. if the past performances have revealed that he/she did not make any large mistakes, he/she follows the Bayesian decision making process. In other words, past performances affect an individual Bayesian learner’s decision making process only when he/she made too many mistakes in the past. Indeed, our theoretical prediction is supported by the recent empirical evidence by reference [1] where they examined how the past performance affects mutual fund tracking error. Secondly, we run a series of Monte Carlo simulations for two different model versions; a simple one without Bayesian learning and an alternative one incorporating Bayesian learning. We compare the results for each version for two alternative scenarios one with a massive, systemic shock and the other without such shocks. A recent, real-life example of a massive, systemic shock is the of course the GFC. Many individuals who had previously thought that their savings were well on track to fund their (for some imminent) retirement, were subjected to great disappointment and distress.
An improved understanding of the process by which such shocks affect the accumulation of retirement funds would clearly be useful. A naïve solution to the dynamic retirement planning problem for an individual would be to redirect all savings to proxy risk-free assets. However because of the very low rates of return and the threat of inflation this approach would not be favorable (or even practical). A better solution ought to involve a dynamic funds allocation strategy that takes into account the individual planners prediction of the state of financial markets as well as the effect of past errors in prediction. This is what we have posited and illustrated in this paper.
2. Brief Review of Extant Literature
Reference [2] recognized that finding a way around the first principle problem is a key issue that lies at the heart of a quintessential social security problem. Effectively the retirement planning problem can be viewed as a special form of the social security problem where targeting the saving goal at retirement age and subsequently determining how to achieve that target is a crucial factor in addressing this problem. The extant literature has mostly addressed this problem via modern portfolio theory [3] [4] or more recently via optimal stopping rule with state constraints [5] . The problem is typically formulated and solved with the help of optimal control theory in either continuous time space or discrete time space [6] . In the most cases, the continuous time space is much easier to solve than that of discrete time space. However, the latter technique is preferable in terms of a more transparent representation of the solution method; especially with regards to its actual application in funds management [7] [8] . In a seminal work of reference [9] , the classical dynamic programming approach is embellished by incorporating a suite of key behavioral and situational factors (e.g. an individual agents belief, age, nature of employment etc). However, these factors are incorporated via pre-set parameters and the only stochastic element in the model is the probabilistic equation of motion (i.e. the standard Markov process). Most of the later models were minor extensions of the reference [9] ’s model [8] .
As summarized by reference [10] any Finite Horizon Dynamic Programming (hereafter FZDP) problem is defined by a tuple , where S, A and T are state space, action space and positive integer that incorporates the time horizon respectively. Here, is the reward function; is the equation of motion and corresponding feasible action. To ensure that the target fixed point will be arrived at some additional assumptions are needed, among which the two main ones are: 1) is concave and 2) obeys a Lipschitz condition of contraction mapping.
The standard model of dynamic programming assumes that the knowledge of parameter is known, thus the learning is complete. Indeed, it is quite possible to argue that an individual agent does not know the true state of the market, but may receive a signal of the future direction (i.e. form a prediction about the future state of the market). Such a signal plays an important role in helping the individual agent decide on an action. Given that an individual agent is rational, it may be assumed that he/she engages in Bayesian learning. In this respect, reference [11] has demonstrated how Bayesian learning can be incorporated in dynamic programming to make an optimal decision. Later, the reference [12] has incorporated bayesian learning to show how such learning affects asset prices empirically. In this paper, we are extending reference [11] ’s paper by introducing the conviction function. A “conviction function”, which is a function of past prediction errors, builds persistence, making histories of past shocks to affect the value function that agents use in order to make savings choices. Thus it is not just the signal (i.e. the prediction) but the conviction function in conjunction with the signal that ultimately determines the action. The conviction function is something that is not built into classical dynamic programming, thus we regard this as the most significant methodological contribution of our paper.
Note that, in a discrete-event case, the backward induction technique starts with the last period and works its way backwards period by period to the initial period to establish an optimal time path. However, in so doing, it ignores the forward looking induction. A key decision-making task precedes every state variable taking on a particular value before the true nature of a state is revealed; an individual agent has to decide whether or not to take a certain course of action given how he/she understands the signals, and also given his/her conviction function as determined by past prediction errors. This idea is similar to reference [13] , who introduced the concept of forward looking induction in the context of sub-game perfect Nash equilibrium. However, unlike reference [13] we apply the forward looking induction in a recursive way through Bayesian learning.
3. Model
3.1. Utility, Strategy and Payoff
Consider an individual agent who lives for periods, where ; and dies at period . Thus the terminal period is . An individual agent’s decision variable is at period t, where . This is interpreted as a choice of his consumption at period t so that he can achieve the targeted level of asset at period t. We assume that (since agent dies at period). Each individual agent starts with the initial asset level at periods i.e. our initial condition. Like conventional literature of dynamic programming, we assume that an individual’s utility function is time additive separable (hereafter, TAS) and it is concave with respect to decision variable . Without loss of generality, we assume that an agents’s utility function will be as follows: , where b is a discount factor. All individual agents are homogenous in their preferences.
The state variable evolves with the following equation of motion: i.e. the next period targeted asset level depends on the previous period’s asset level less the choice of consumption at period t, that is the net saving. Here, . Note that, and are the returns from the risky and safe investments respectively such that . In our set-up, we assume that an individual can choose either or i.e. to invest his saving either in the risky asset or in the safe asset.1 In the case of risky asset investment, we assume that the return of risky asset, , (as we have mentioned in the equation of motion) follows the Markovian probability . In other words, in the case of risky asset, there is probability a to obtain , if so then the probability to obtain 0 is . However, the return of safe asset follows the Markovian probability i.e. the probability to obtain is always 1. Clearly, a is very important for the risky investment and the nest two sections, we develop the conviction function in conjunction with Bayesian learning and define a in terms of conviction function.
3.2. Signals and Bayesian Learning
Consider the following scenario. An individual agent does not know how well the economy will perform at the beginning of each period , however, he/she knows with certainty that there are only two possible outcomes; and (i.e. good and bad states respectively) with equal probability. This implies that an individual’s prior belief is . Furthermore, an individual
receives signals g and b at the beginning of each period. We assume that these signals are symmetric binary by nature. In others words, there is probability p that both the state and signal will be matched, otherwise there will be mismatched outcome with the probability . Table 1 summarizes the situation:
It should be noted that in our model we consider two different types of states: one is the state variable that evolves from the equation of motion, and the other is the state of economy’s performance (which depends on the agent’s Bayesian learning). From the above table, one can calculate the following Bayesian Probabilities (P):
(1)
Table 1. States and symmetric binary signals.
Equation (1) defines the following rules, which are crucial for agent’s decision making process:
Definition 1 Given the symmetric binary signal, the following defines the ex-ante rules for decision making process at period t:
1) If , an individual agent will form a posterior belief that there is a match between his/her signal and the state of economy’s performance. In this case, he/she will follow his signal i.e. if he/she receives g, he/she will choose signal ; and if he/she receives signal b, he/she will choose .
2) If , an individual agent will form a posterior belief that there is a mis-match between his/her signal and the state of economy’s performance. In this case, he/she will always play safe i.e. he/she will choose .
Definition 1 accords with our intuition. Suppose, an agent receives signal b. Given signal b, the state of economy’s performance is either and . From the symmetric binary signal he/she knows that and . He/she forms his/her posterior belief that his/her signal is matched with the state of economy’s performance if .
3.3. Conviction Function
Although Definition 1 explains how a decision will be made given the signal for the current period, it does not tell how a decision is made when an agent has perfect recall of the success or failure of past predictions. Indeed, past history may affect agent’s belief and make him/her less confident about his/her current signal or the other way around. To make it clear, let assume that agent is at period . He/she can observe whether his/her decision at period t was right or wrong by observing the state variable at current period (i.e. in our model ). In so doing, he/she will follow the following steps:
At period t, ex-ante, an agent has received signal g with , thus according to Definition 1, he/she thinks there is a match between his/her signal and state of economy’s performance i.e. and takes his/her decision accordingly.
At period , ex-post, an agent has realised whether he/she made a mistake or not by observing the state variable . If he/she made a mistake that implies that and . Thus, the magnitude of error at period t, denoted as , is as follows: . Note that, if the agent does not make a mistake then .
Suppose, an agent receives the same signal g at period and, like Step 1, he/she calculates the same posterior belief. Thus ex-ante if an agent has received signal g with , he/she might think that a match between his/her signal and the state of economy’s performance (following the Definition 1). However, this is true only if i.e. he/she did not make any mistake in last period. If an agent made a mistake in last period, the current signal is not enough to build his/her confidence level to choose the same action that he/she took in last period. In this case, an agent has to revise his/her confidence level. Thus if he/she receives g signal, the strength of the signal g at period is measured as follows: . Agent will be confidence enough that his/her signal is matched with the economy’s performance if the following is true:
(2)
This implies that an agent will be confident enough that his/her signal is matched with the current performance of an economy if his/her signal . It should be noted that when the agent made a mistake at period t. Hereafter, refers to an agent’s confidence function about his/her signal at period .
Given condition (2) and the process describe in the above three steps, the same procedure can be generalized for periods, where . Suppose at period n an agent receives signal g with probability p and revises his/her confidence level based on whether his/her signal is matched with current performance of the economy. From the history of past periods, the agent learns that his/her signals were correct for k periods, and thus periods his/her signals were incorrect. Therefore, at period n, condition (2) will be as follows:
(3)
Equation (3) leads to following proposition:
Proposition 1
If i.e. agent does not make any mistakes in any of the previous periods, then .
If i.e. agent makes mistakes for periods then .
If i.e. agent makes mistakes for all n periods then . And if .
Proof. The proof follows from Equation (3) and the argument lies in those three steps.
Proposition 1 is explains how an agent learns from his/her past decisions and build his/her conviction function . The important part is that by introducing , we analyze the role of forward looking induction in the dynamic programming which might lead to different dynamic paths as oppose to dynamic path suggested by Bellman equation.
We are now able to define a in terms of . Indeed, for any period , a is defined as follows: . Note that, if one has made a lot of mistakes in the past, one will have higher value of (see Proposition 1(B)) in that case, one will face lower value of a, i.e., the probability will be very less that one will reach in the next state with the higher return . If one does not make any mistake then (see Proposition 1(A)) in that case (in other words, the value of a is exactly equal to one’s Bayesian signal i.e. ). Although the main contribution of our paper is Proposition 1, we also provide an example in Appendix illustrating the role of the conviction function in a finite horizon decision set-up.
4. Numerical Rendition
We present a numerical rendition of the dynamic optimization problem as posited and developed in the previous sections. For purpose of computational tractability, we have limited an individual agents planning horizon to five discrete time periods (six nodes) with a time-line going from t0 to t5.
At each node there are two possible, mutually exclusive events either the signal matches the true state of the market (i.e. there is no prediction error) or the signal does not match the true state of the market (i.e. there is a prediction error). Also, at each node the individual agent chooses a certain course of action and for the sake of simplicity, we limit the pertinent action space to a set of two mutually exclusive choices either the individual agent opts for a risky pool of assets or he/she opts for a riskless pool of assets. The starting amount in the retirement fund (i.e. y0) is set as 1.0. Given the agent opts for the risky portfolio, the payoff from a match is while the payoff from a mismatch is . If on the other hand if the agent opts for the riskless portfolio then the payoff is 0.05 in both cases (i.e. irrespective of whether it’s a match or a mismatch) as by definition this is a risk free outcome. The riskless portfolio if chosen in each of the five periods, would ensure a certain ending amount of 1.25 at the end of the fifth period irrespective of whether or not the signal matched the true state (i.e. whether or not the predictions were correct) in any of the past periods. Therefore this serves as a baseline value and realistically, all targeted amounts should be above this baseline. Given our starting numerical values as stated above, the four potential targets are 1.50 (best of the lot; with no past errors), 1.45 (achievable with at most one past prediction error), 1.40 (achievable with at most two past prediction errors), 1.35 (achievable with at most three past prediction errors) and 1.30 (achievable with at most four past errors).
For each period therefore, there may be a match or a mismatch of signal and true state for one, some or all previous periods and a corresponding outcome depending on whether a risky or a riskless portfolio was chosen by the agent in each of those previous periods. This effectively results in an event-action matrix of dimension , which as one may construe, could become inordinately large even for a moderately large value of n and quickly approach the limits of computability. For a fairly small n = 5, we have constructed a matrix representing all the possible time paths from y0 to y5 that the individual agent could follow.
The results obtained from the 32 × 32 event-action matrix are summarized in Table 2.2
Table 2. Numerical output obtained from the posited theoretical model for n = 5.
The percentage figures (in bold italicized font) represent the percentage drops in likelihood of achieving the best outcome for the particular time path for the highest number of past errors for which that best outcome is achievable. So, for example, for a targeted best possible outcome of 1.45 (i.e. the maximum amount an individual agent can expect to have accumulated at the end of the given planning horizon), the probability of achieving the target drops by 48.5% for a single past prediction error. For two past prediction errors, this probability drops by 100% i.e. the target no longer remains achievable (and would have to be revised downward to the next highest number of 1.40). Again; for a targeted best possible outcome of 1.40, the probability of achieving the target drops by 66% for two past prediction errors. For three past prediction errors, this probability drops by 100% i.e. the target no longer remains achievable (and would have to be revised downward to the next highest number of 1.35); and so on. It is interesting to note that these percentages can be seen to closely approximate the ratio ; where is the conviction level predicted by our theoretical model for a given number of past prediction errors. For 1 prediction error and (corresponding to a 48.5% drop in the likelihood of achieving the target of 1.45), for 2 prediction errors and (corresponding to a 66% drop in the likelihood of achieving the target of 1.40); for 3 prediction errors and (corresponding to a 73% drop in the likelihood of achieving the target of 1.35) and for 4 prediction errors and (corresponding to a 76% drop in the likelihood of achieving the target of 1.30).
It must be noted that this numerical rendition does not incorporate a massive exogenous shock (reminiscent of the GFC) but is rather a straightforward numerical demonstration of how the dynamic time paths would pan out for all possible combinations of event and action and shows how learning might be organically embedded in the temporal evolution process. By incorporating the conviction level (a function of past prediction errors) into the decision process along with the signal generated in each period, an individual agent is better able to identify the optimal path into the future given his/her present location in any intermediate node. For example, if an agent is at the beginning of the fifth (i.e. terminal) period and has only one prediction error till that point, then he can reach at best 1.45 (if he/she selects the risky portfolio and there’s a match of signal with true state in the last period) or, at worst, he/she can reach 1.40 (if he/she selects the risky portfolio and there’s a mismatch of signal with true state in the last period) so will always select risky if target . On the other hand, if the agent has made two prediction errors already, then he/she can reach 1.40 at best (if he/she selects the risky portfolio and there’s a match of signal with true state in the last period) so will need stronger conviction to opt for risky in the last period.
In the next section we firstly present the results of Monte Carlo simulations for two different cases a naïve case (without learning) and an alternative one (with learning). For each of these cases, we have two alternative scenarios one with a massive exogenous shock (reminiscent of the GFC) and the other without a shock. We then discuss the results in detail.
5. Monte Carlo Simulations
To allow for a more realistic presentation of the implications of the theoretical model the simulations is set up in such a manner that it is representative of an individual who saves for retirement over a 40 year working career. At the end of each month the individual observes the performance of the financial market over the last month and formulates a decision as to how the accumulated assets should be invested for the following month.
As in the theoretical formulation of the model, financial markets have only two states; high returns or low returns. In the simulation the return when the market is “high” is set at 1.0% per month, and when the market is “low” there is a negative return of 0.85% per month. The state of the market in any one period is modeled as a binomial random variable with a 50% probability of a high or low outcome. This effectively gives a slightly positive return to the overall market in the longer term. There is also a “safe portfolio” and this is set to give a return of 0.1% per month. We consider two cases; one in which the individual “remembers” his past mistakes and the other in which there is no memory of the past. Without memory of past mistakes the individual has no reason not to be optimistic and will thus invest in the risky portfolio in each period. However if past mistakes are remembered then the theoretical model is used to determine if the individual invests in the risky portfolio or the safe portfolio. Without loss of generality an initial investment of $1000 at the beginning of the period is made, and the total reinvested each period. The results of 2000 iterations of the simulation are shown is Figure 1.3 The fact that there is little difference in the situations with and without memory is as expected. The recall of past mistakes does not lead to an advantage in asset selection since it does not provide any advantage in predicting the future course of the market.
In order to test for the effect of an external shock to the system the simulation is adapted so that a period of “low” returns is forced into the stream of market conditions. Since individuals can experience such as shock at various times in their working career, this string of low returns is inserted randomly into each of the 40 year working careers that are simulated. A shock of 120 consecutive periods of low returns is therefore introduced. All other conditions remain as per
Figure 1. Value of retirement savings, with no external shock.
the first simulation. The results are shown in Figure 2.4
The value of retirement savings falls for both sets of individuals because of the crisis, but the individuals with learning do better. This is not because they are better at predicting the outcome of the market, but because when they experience negative outcomes they adjust by holding the safe portfolio until they have experience enough signals that are correct for them to once again invest in the risky portfolio.
6. Conclusion
The significance of our research is two-fold. Firstly, we have proposed and formally derived an extension to the classical dynamic programming model via incorporation of a Bayesian learning component. Apart from theoretically deriving this extension, we have applied it in the practical context of a retirement savings planning problem whereby an individual agent starts with a given amount in his/her retirement fund and then tries to optimally manage it over a finite time horizon so as to attain a certain minimum target value. The model takes into consideration the risk propensity of the individual agent and yields a trivial solution as per intuition if the target minimum value is less than or equal to the maximum value attainable via risk-less investing. The numerical rendition illustrates that for every past prediction error, the highest possible target end value of the retirement fund would have to be revised downward with an associated drop in the probability of achieving the target for each additional error made. Clearly then, if the individual agent was “learning” from the past errors and thereby becoming more and more “stringent” in terms of the minimum signal strength required to induce a selection of the risky portfolio, the riskless portfolio would be opted for more and more as the number of past errors increased. This would effectively help to “lock in” the fund value to a certain target end value with lower and lower likelihood of any further downward adjustment. Our
Figure 2. Value of retirement savings, with no external shock.
posited “conviction function” allows for a neat integration of the Bayesian learning component with the classical Bellman principle of dynamic optimization and therefore makes a significant contribution to optimization theory. Finally, our Monte Carlo simulations (using hypothetical numbers) clearly illustrate how the posited model would work in reality, particularly in the event of a large exogenous shock to the investment market (reminiscent of the GFC), thereby further highlighting its practical significance in financial planning.
Cite this paper
Cohen, M., Nabin, M., Bhattacharya, S. and Kumar, K. (2018) Conviction Function? A New Decision Paradigm for Personal Financial Risk Management in the Face of Large Exogenous Shocks. Theoretical Economics Letters, 8, 918-934. https://doi.org/10.4236/tel.2018.85065
References
- 1. Wang, C.P., Huang, H.H. and Chen, C.Y. (2015) Does Past Performance Affect Mutual Fund Tracking Error in Taiwan? Applied Economics, 47, 5476-5490.
- 2. Diamond, P.A. and Orszag, P.R. (2005) Saving Social Security. Journal of Economic Perspectives, 19, 11-32. https://doi.org/10.1257/0895330054048722
- 3. Markowitz, H. (1952) Portfolio Selection. The Journal of Finance, 7, 77-91.
- 4. Rubinstein, M. (2002) Markowitz Portfolio Selection: A Fifty-Year Retrospective. The Journal of Finance, 57, 1041-1045. https://doi.org/10.1111/1540-6261.00453
- 5. Dybvig, P.H. and Liu, H. (2015) Verification Theorems for Models of Optimal Consumption and Investment with Retirement and Constrained Borrowing. Mathematics of Operations Research, 19, 11-32.
- 6. Bhattacharya, S. and Khoshnevisan, M. (2005) A Proposed Fuzzy Optimal Control Model to Minimize Target Tracking Error in a Dynamic Hedging Problem with a Multi-Asset, Best-of Option. Journal of Asset Management, 6, 136-140. https://doi.org/10.1057/palgrave.jam.2240171
- 7. Rust, J. (1987) A Dynamic Programming Model of Retirement Behavior. http://www.nber.org/books/wise89-1 https://doi.org/10.3386/w2470
- 8. Aguirregabiria, V. and Mira, P. (2010) Dynamic Discrete Choice Structural Models: A Survey. Journal of Econometrics, 156, 38-67. https://doi.org/10.1016/j.jeconom.2009.09.007
- 9. Rust, J. and Phelan, C. (1997) How Social Security and Medicare Affect Retirement Behavior in a World of Incomplete Markets. Econometrica, 65, 781-831. https://doi.org/10.2307/2171940
- 10. Sundaram, R.K. (1996) A First Course in Optimization Theory. Cambridge University Press, Cambridge, UK.
- 11. Cogley, T. and Sargent, T.J. (2008) Anticipated Utility and Rational Expectations as Approximation of Bayesian Decision Making. International Economic Review, 49, 185-221. https://doi.org/10.1111/j.1468-2354.2008.00477.x
- 12. Lu, K.Y. and Siemer, M. (2013) Learning, Rare Disasters and Asset Prices. Working Paper in Finance and Economics Discussion Series, Washington, D.C.
- 13. Kohlberg, E. and Mertens, J.-F. (1986) On the Strategic Stability of Equilibria. Econometrica, 54, 1003-1037. https://doi.org/10.2307/1912320
1. Appendix
1.1. Example: Finite Horizon Decision Making Process and Conviction Function
In order to obtain a closed form solution we assume that .5 Therefore, we can formulate the finite horizon dynamic problem as follows
(4)
(5)
(6)
(7)
In order to solve the above problem, we assume that an individual agent is making his/her decision at period n. At period n, he/she knows for sure that how many mistakes he/she made in the past periods. Furthermore, we assume that, one has made mistakes in the past. In other words, he/she made correct decisions in k periods. In these k periods, he/she may have made both risky and safe investments. Suppose, he/she makes successful risky investment for x periods; and he/she makes safe investment for periods. Thus his initial asset accumulation at period is as follows:
(8)
In period n, the value function (following from Bellman’s optimal principal) one faces is as follows:
(9)
Similarly, in period , the value function will be as follows:
(10)
Both Equations (9) and (10) are key to find out the Bellman’s Optimal principle. The solutions of Equations (9) and (10) are discussed in the next section.
1.2. Solution
One can easily solve Equations (9) and (10) with the help of Equations (5) to (8). The optimal solutions are provided as follows:
(11)
(12)
(13)
(14)
By using Equations (8), (12) and (14) we obtain the asset value in period , which is as follows:
(15)
If one chooses to invest in the risky asset for two successive periods (provided that he/she does not make any mistake) then the Equation (15) will be as follows:
(16)
On the other hand, if one chooses to invest in the safe asset for two successive periods (provided that he/she does not make any mistake) then the Equation (15) will be as follows:
(17)
Note that, following from Proposition 1(B), the value of
when 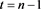 will be
will be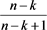 . Thus comparing Equations (16) and (17), one will invest in risky asset if the following condition is met:
. Thus comparing Equations (16) and (17), one will invest in risky asset if the following condition is met:
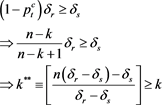 (18)
(18)
Equation (18) develops the following Lemma:
Lemma 1 There exists 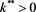 such that if
such that if 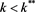 then an individual decision maker will choose to invest in the risky asset. On the other hand if
then an individual decision maker will choose to invest in the risky asset. On the other hand if  then an individual investor will invest in the safe asset.
then an individual investor will invest in the safe asset.
Proof. The proof follows from Equation (18).
Lemma 1 implies that there exists a critical level for the periods of correct decision making, 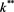 , in conjunction with conviction function such that if
, in conjunction with conviction function such that if 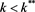 then an individual decision maker invests in the risky asset since the expected benefit from investing on such asset will be higher. However, the reverse will be true if
then an individual decision maker invests in the risky asset since the expected benefit from investing on such asset will be higher. However, the reverse will be true if 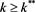 i.e. in this case safe investment gives higher return.
i.e. in this case safe investment gives higher return.
Interesting question one might ask is that how the above outcome based on conviction function differs from the outcome based on Bayesian learning. The answer lies on what values a will take based on Bayesian learning only (follows by Definition 1) when one chooses to invest on risky asset ( ). Indeed, in such case, a takes the following value:
). Indeed, in such case, a takes the following value:
 (19)
(19)
However, with the conviction function one faces the following value of a
 (20)
(20)
Here,  refers past history where k number of periods an individual investor makes correct decisions in making investment on risky asset. Equation (19) will be special case of conviction function (follows from Proposition 1(A) and 1(C)). Thus without conviction function a will be either overestimated or underestimated which makes an individual investor too much optimistic or too much pessimistic. Indeed, Equation (20) is methodologically novel in a sense it not only incorporates Bayesian learning from current signals but also incorporates the learning from past mistakes.
refers past history where k number of periods an individual investor makes correct decisions in making investment on risky asset. Equation (19) will be special case of conviction function (follows from Proposition 1(A) and 1(C)). Thus without conviction function a will be either overestimated or underestimated which makes an individual investor too much optimistic or too much pessimistic. Indeed, Equation (20) is methodologically novel in a sense it not only incorporates Bayesian learning from current signals but also incorporates the learning from past mistakes.
NOTES
1One can also consider the convex combination of and , however, this will not change the qualitative result of our model.
2Note: All numbers are hypothetical and intended for illustration only no primary or secondary data sources have accessed for the purpose of this research.
3Note: All numbers are hypothetical and intended for illustration only no primary or secondary data sources have accessed for the purpose of this research.
4Note: All numbers are hypothetical and intended for illustration only no primary or secondary data sources have accessed for the purpose of this research.
5Note that, this assumption is standard in the literature of economics where the utility function is subject to diminishing return.




