Theoretical Economics Letters
Vol.05 No.04(2015), Article ID:58937,5 pages
10.4236/tel.2015.54065
An Empirical Multi-Output Production Decision Model for the Profit Maximizing Multiproduct Firm
Ekaterina Vorotnikova1, Serhat Asci2
1Agricultural Economics and Rural Sociology Department, University of Idaho, Moscow, ID, USA
2Department of Agricultural Business, California State University, Fresno, CA, USA
Email: evorotnikova@uidaho.edu, sasci@csufresno.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 July 2015; accepted 17 August 2015; published 20 August 2015
ABSTRACT
Empirical estimation of a theoretical multi-output production model that uses multiple inputs is difficult because of the complexities of its functional form. By using proper parameterization to linearize theoretical model’s functional form, this paper develops an empirical estimation for multi-output production decision using multiple inputs in the profit maximizing firm, namely, multi-output production decision model. The model aligns with the dual approach of cost minimization and revenue maximization for the profit maximizing multi-product firm while keeping jointness in production structurally intact.
Keywords:
Multiproduct Firm, Multi-Output Production Decision, Differential Production Component

1. Introduction
[1] developed a theory of multiproduct firm and used a differential approach to model a multi-output production using multiple inputs. They theoretically derived input demand and output supply equations for multiproduct firm. The authors also extended these derivations to the input allocation decision for the cost minimizing, the revenue maximizing firms, as well as multi-output production decision for the profit maximizing firms. However, the complexities of the equations presented some barriers to empirical estimation of such models. This paper developed an empirical estimation model for multi-output production decision using multiple inputs in the profit maximizing firm, namely, multi-output production decision model.
[2] comprehensively derived input demand and output supply systems and exemplified the estimation of these systems. However, he recommended imposing input-output separability restriction to simplify the input allocation and multi-output production decision models for estimation. This restriction resulted in input allocation decision independent of the changes in output prices and multi-output production decision independent of the changes in the input prices, which was counterproductive to the multiproduct firm theory.
Recently, [3] and [4] developed empirical models to estimate input allocation in the revenue maximizing and the cost minimizing firms, respectively. These empirical models linearized functional forms of the input allocation models without having to impose the input-output separability and input independence restrictions. Additionally, the authors suggested a statistical test, which checked whether imposing these restrictions was necessary. By using this linearization technique, we developed an empirical model for the multi-output production decision for the profit maximizing firm that combined both cost minimization and revenue maximization for a particular firm. We also proved homogeneity property for the individual input price parameter for each output.
[5] and [6] estimated output-supply model. However, no one to date had empirically estimated multi-output production decision model due to the complexities associated with the input price terms. This paper reformulated multi-output production decision model for the profit maximizing firm by using proper parameterization to linearize theoretical model’s functional form. This advancement allowed us develop multi-output production decision model that could easily be estimated empirically.
The empirical model suggested that multi-output production decision was a function of the Divisia output volume index and the relative changes in the individual input and output prices. The model was derived in such a way that the theoretical adding-up conditions held for all parameters. The restrictions like homogeneity, symmetry, input-output separability and output independence cpuld be imposed and tested statistically.
The paper was organized in the following way: Section 2 developed the multi-output production decision model for profit maximizing firm. Section 3 linearized and reformulated the model empirically, and Section 4 concluded the paper.
2. Multi-Output Production Decision Model for Profit Maximizing Firm
Profit maximizing multiproduct firm implies the following multi-output production decision equation for the rth product [1] [2]
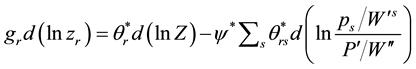 (1)
(1)
where  is the rth output’s share in revenue; zr is the quantity of the rth output; pr is the price of the rth output
is the rth output’s share in revenue; zr is the quantity of the rth output; pr is the price of the rth output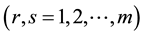 ;
;  is a Divisia output volume index;
is a Divisia output volume index; 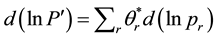 is a Frisch output price index where pr is the price of the rth output;
is a Frisch output price index where pr is the price of the rth output;
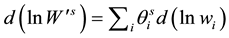 and
and 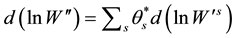 are Frisch input price indexes where wi is the price of the ith input
are Frisch input price indexes where wi is the price of the ith input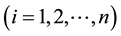 . The coefficient
. The coefficient  is normalized output price coefficient and represents a
is normalized output price coefficient and represents a
pure substitution effect between the rth and sth products. Therefore, we define 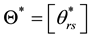 is an m × m symmetric positive definite matrix,
is an m × m symmetric positive definite matrix,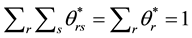 . In addition,
. In addition,  ,
,  is de-
is de-
scribed as the rth product marginal revenue for the ith input. 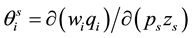 expresses the additional cost of the ith input used in the production relative to the additional dollar’s value of the sth output as a necessary condition for profit maximization.
expresses the additional cost of the ith input used in the production relative to the additional dollar’s value of the sth output as a necessary condition for profit maximization. 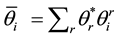 is such that
is such that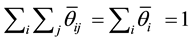 , where
, where 

Finally, the revenue-cost ratio is 







Note that when the firm is input-output separable, the multi-output production decision model becomes independent of the input price changes. This restriction implies that the individual input price indexes are the same
for each output. Hence, the Frisch input price indexes are equal to each other,


3. Multi-Output Production Decision Model
3.1. Linear Model
This section simplifies Equation (1) to a linear form. We can show Equation (1) as the three-term summation:

When we decompose output price terms into two terms using the above definition, 

Collecting under output price term, the two terms can be written as

where 



Then, we rewrite the last term of Equation (2) as, 


By using 


We substitute 

By distributive property, we rewrite expression (7) as













Substituting simplified terms into expression (8) yields

Define 

The properties of the parameters are demonstrated in Appendix B. In summary, all parameters automatically hold the adding-up condition, 




output price parameters 


3.2. An Empirical Model
We parameterize Equation (10) by assuming





To estimate parameter, we calculate arithmetic means of output shares,



The model naturally maintains the adding-up conditions. Symmetry conditions on 



After dropping one equation we estimate the remaining m-1 equations simultaneously [7] . Maximum likelihood or iterative seemingly unrelated regression (SUR), which also iterates to maximum likelihood [8] [9] , can estimate the parameters



where input prices disappear from the linear form. Further output separability restriction simplifies Equation (12) to

Both restrictions can be tested with an LRT.
4. Conclusions
This study makes it possible to empirically estimate the decision model that optimizes the production process with multiple inputs being used across multiple outputs. The model aligns with the dual approach of cost minimization and revenue maximization for the profit maximizing multi-product firm while keeping jointness in production structurally intact.
We reformulate multi-output production decision model by using proper parameterization to linearize theoretical model’s functional form. Homogeneity property for the individual input price parameter for each output is formally proven, which is never done before.
Cite this paper
EkaterinaVorotnikova,SerhatAsci, (2015) An Empirical Multi-Output Production Decision Model for the Profit Maximizing Multiproduct Firm. Theoretical Economics Letters,05,555-560. doi: 10.4236/tel.2015.54065
References
- 1. Laitinen, K. and Theil, H. (1978) Supply and Demand of the Multiproduct Firm. European Economic Review, 11, 107-154. http://dx.doi.org/10.1016/0014-2921(78)90031-4
- 2. Laitinen, K. (1980) A Theory of the Multiproduct Firm. In: Theil, H. and Glejser, H., Eds., Studies in Mathematical and Managerial Economics, North Holland, New York, 28.
- 3. Seale Jr., J.L., Vorotnikova, E. and Asci, S. (2014) An Empirical Input Allocation Model for the Multiproduct Firm. Economics Letters, 124, 367-369. http://dx.doi.org/10.1016/j.econlet.2014.06.021
- 4. Zhu, M., Onel, G. and Seale Jr., J.L. (2015) An Empirical Input Allocation Model for the Cost Minimizing Multiproduct Firm. Economics Letters, 132, 73-76. http://dx.doi.org/10.1016/j.econlet.2015.04.015
- 5. Clements, K.W. (1980) An Aggregative Multiproduct Supply Model. European Economics Review, 13, 239-245. http://dx.doi.org/10.1016/0014-2921(80)90057-4
- 6. Rossi, N. (1984) The Estimation of the Product Supply and Input Demand by the Differential Approach. American Journal of Agricultural Economics, 66, 368-375. http://dx.doi.org/10.2307/1240804
- 7. Barten, A.P. (1977) The Systems of Consumer Demand Functions Approach: A Review. Econometrica, 45, 23-50. http://dx.doi.org/10.2307/1913286
- 8. Harvey, A. (1990) The Econometric Analysis of Time Series. 2nd Edition, The MIT Press, Cambridge.
- 9. Kmenta, J. and Gilbert, R.F. (1968) Small Sample Properties of Alternative Estimators of Seemingly Unrelated Regressions. Journal of the American Statistical Association, 63, 1180-1200. http://dx.doi.org/10.1080/01621459.1968.10480919
Appendix A: Simplification of Summation Terms
The expression 
Using

In explicit form, 

Further rearrangement and simplification, it yields

and we can write this simplified expression as
Appendix B: Properties of Parameters
Define

and hence, 


Lastly, symmetry holds for m × m matrix, where
Define



Individually summing over r and i, respectively, yields
and
for the parameter with m × n dimension.
Define

and hence, 

Lastly, symmetry does not hold for m × n matrix.







