Theoretical Economics Letters
Vol.04 No.09(2014), Article ID:52185,4 pages
10.4236/tel.2014.49106
Market Middlemen and Determinants of the Price Spread under Competition
Michael K. Wohlgenant
Department of Agricultural & Resource Economics, North Carolina State University, Raleigh, North Carolina, USA
Email: michaelwhlgnnt@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 October 2014; revised 20 November 2014; accepted 4 December 2014
ABSTRACT
Neoclassical economics is shown to yield predictions consistent with empirical industrial organization models regarding market middlemen behavior. Diminishing marginal returns to use of variable factor inputs produces three important predictions: a) the price spread between the output price and raw material price is positively correlated with output price, b) the raw material quantity is positively correlated with the price spread, and c) the price spread is positively correlated with other variable factor prices. An application to US farm-to-retail price spread time series data shows the consistency of the predictions.
Keywords:
Middlemen, Diminishing Marginal Returns, Competition

1. Introduction
Diminishing marginal returns is a cornerstone of neoclassical economics and defines the relevant region for production for a competitive firm. The purpose of this article is to show that it is relevant to even market middlemen, a group of traders/merchants who are often alleged to operate in imperfectly competitive markets. Existence of a market middlemen, like any firm, exists to overcome transaction costs. Spulber [1] and Rust [2] show that an efficient market outcome can exist with heterogeneous consumers, producers, and market middlemen with transaction and search costs. These results, while useful in establishing the important finding that market middlemen can be efficient, fall short of providing a theory and models that can produce testable implications with market-level data. This article shows that even the more basic assumptions of price taking behavior and a production function exhibiting diminishing marginal returns produces predictions that are general and easily implemented empirically.
The empirical literature on the determimants of price spreads of market middlemen is generally based on ad hoc specifications of markup behavior or from reduced form models derived from structural models of supply and demand [3] . The most structural specification available, called the relative price spread model [4] , specifies the price spread relative to output price as a function of the raw material quantity procured and the price of marketing input prices relative to output price. This article attempts to fill this void by developing a simple model that yields testable predictions that can be confronted with real world data.
2. Neoclassical Theory of Market Middlemen
As observed by Spulber [5] , in reality most middlemen transform products they procure to add value as manufacturers do. Thus, it seems reasonable to approach the problem from a neoclassical approach where the firm possesses a production function used to procure a product from sellers that is combined with other inputs to produce a product that is sold to buyers. Linear homogeneity of the long-run production function is a reasonable assumption in light of the replication argument [6] . Assume a price taking firm combines two inputs, labor
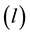 and raw material
and raw material
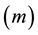 to produce a single output
to produce a single output
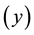 In addition to these inputs there are fixed inputs
In addition to these inputs there are fixed inputs
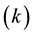 an important subcategory being entrepreneurial capacity [6] which cannot be used anywhere outside the industry in question. This means that the production function of the firm, even in the long run exhibits decreasing returns to scale. Given the long-run assumption of constant returns to scale, we can express the production function as follows:
an important subcategory being entrepreneurial capacity [6] which cannot be used anywhere outside the industry in question. This means that the production function of the firm, even in the long run exhibits decreasing returns to scale. Given the long-run assumption of constant returns to scale, we can express the production function as follows:
 (1)
(1)
With
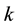 fixed, assume the firm is a price taker in both output and factor markets. Assume also that the firm takes
fixed, assume the firm is a price taker in both output and factor markets. Assume also that the firm takes
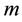 as fixed in determining its profit-maximizing input levels1. The first-order conditions for profit maximization conditional on
as fixed in determining its profit-maximizing input levels1. The first-order conditions for profit maximization conditional on
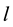 are:
are:
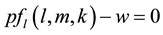 (2)
(2)
where
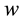 is the wage rate. Solving for the optimal
is the wage rate. Solving for the optimal
 and substituting back into the profit equation produces the conditional profit function,
and substituting back into the profit equation produces the conditional profit function,
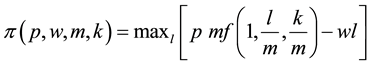 (3)
(3)
Application of Roy’s identity to this profit function with respect to output price and raw material quantity yields the conditional output supply and inverse raw material demand functions:


where




Proposition 1.
Proof. The conditional output supply function can be written as




Proposition 2.
Proof.


Theorem 1.
Let the price spread between the raw material and final product be defined as
where



Proof. i) Differentiate




ii) Differentiate the price spread function with respect to


iii) Differentiate the price spread function with respect to




two-input case. However, with more than two inputs the sign will be indeterminate. □
In summary, neoclassical economics yields definite predictions about the behavior of the price spread in response to changes in output price and quantity of the raw material input. The relationship between the price spread and output price is a relationship that theory predicts will hold because of diminishing marginal product of the raw material input (Proposition 1). The importance of this is that neoclassical price theory can, in fact, account for markup pricing even in the absence of market power Figure 1 shows how important this relationship is for an important commodity, U.S. beef farm-to-retail price spread in relationship to retail beef price.
Figure 1. Relationship between beef price spread and retail beef price (cents/lb.), 1970-2012.
3. Empirical Application
The price spread equation can be quantified with time series and/or cross-section data in the aggregate or at the individual firm level. To illustrate the importance and predictability of the results established in Theorem 1, I estimate the relationship between the farm-to-retail price spread for beef as a function of the retail price, an index of food marketing input prices, and the quantity of cattle slaughtered. This price spread is an excellent example of middlemen behavior that involves the whole gamut of processing, marketing, and distributing of a product. Annual data from 1970-2010 are used. Because of unit roots in all the series, I first deflated all the data by the overall Consumer Price Index (CPI) and also included trend


The results are entirely consistent with Theorem 1. The price spread is significantly positively related to retail price and quantity of the raw material processed and marketed. Although the wage rate is not significant it is positive as expected. As indicated previously, the first difference variables are included to correct the standard errors for effects of unit roots. They also correct for endogeneity [8] .
4. Conclusions
I have shown how neoclassical economics can account for some important features of market middlemen behavior often assumed to result because of market power. Competitive theory with profit maximizing behavior is shown to yield three important predictions: a) a positive relationship between the price spread and output price, b) a positive relationship between the price spread and wage rate, and c) a positive relationship between the price spread and raw material quantity processed and marketed. The theory is applied to US beef price spread data and is shown to be completely consistent with the data.
The key to understanding why the model predicts the positive relationship between the price spread and output price is diminishing marginal product of the raw material. The law of diminishing marginal returns implies that when output price rises, the firm is induced to increase output because the raw material price, while rising, will rise less proportionally than output price. This is what can lead to a positive relationship between the price spread and output price as Theorem 1 shows. This provides an alternative explanation to market power being the cause of a positive relationship. The importance of this result is that such behavior, consistent with perfect competition, means market middlemen can indeed add value to the product and increase wealth.
While the analysis here focuses on short-run adjustment, there are reasons to believe it would hold in the long run as well. When there are inframarginal firms, adjustment by these firms would still occur in this same fashion in the long run with entrepreneurial capacity the limiting factor of each firm. The total adjustment would consist of those inframarginal firms and the marginal firms in the industry [9] .
Finally, this is obvious only part of the theory of behavior of market middlemen. Transaction costs are a reason these firms exist to begin with and search costs are clearly important as the literature has underscored. There are also product design and quality issues that are important as well, such as found in [10] . At the very least, we can say that neoclassical economics has something important to say about Market Middlemen behavior and should not be ignored in development of a viable theory.
Acknowledgements
Research supported in part by the North Carolina Agricultural Research Service, Raleigh, North Carolina, 27695.
References
- Spulber, D. (1996) Market Making by Price-Setting Firms. Review of Economics Studies, 63, 559-580. http://dx.doi.org/10.2307/2297793
- Rust, J. and Hall, G. (2003) Middlemen versus Market Makers: A Theory of Competitive Exchange. Journal of Political Economy, 111, 353-403. http://dx.doi.org/10.1086/367684
- Wohlgenant, M. (2001) Marketing Margins: Empirical Analysis. In: Gardner, B. and Rausser, G., Eds., Handbook of Agricultural Economics, Vol. 1, Elsevier Science B.V., Amsterdam, 934-970.
- Wohlgenant, M. and Mullen, J. (1987) Modeling the Farm-Retail Price Spread for Beef. Western Journal of Agricultural Economics, 12, 119-125.
- Spulber, D. (1996) Market Microstructure and Intermediation. The Journal of Economic Perspectives, 10, 135-152. http://dx.doi.org/10.1257/jep.10.3.135
- Friedman, M. (1976) Price Theory. Aldine Publishing Co., Hawthorn.
- Phillips, P. (1991) Optimal Inference in Cointegrated Systems. Econometrica, 59, 283-306. http://dx.doi.org/10.2307/2938258
- Saikkonen, P. (1991) Asymptotically Efficient Estimation of Cointegration Regressions. Econometric Theory, 7, 1-21. http://dx.doi.org/10.1017/S0266466600004217
- Panzar, J. and Willig, R. (1978) On the Comparative Statics of a Competitive Industry with Inframarginal Firms. The American Economic Review, 68, 474-478.
- Buccola, S. (2000) Material and Value-Adding Inputs in Manufacturing Enterprises. Journal of Productivity Analysis, 13, 231-247. http://dx.doi.org/10.1023/A:1007823025460
Notes

1This should not be taken to imply that profit is not maximized with respect to
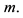 Indeed, the level of
Indeed, the level of
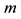 considered could be its optimal value. The reason for optimizing profit conditional on
considered could be its optimal value. The reason for optimizing profit conditional on
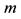 is for analytical purposes to derive an explicit relationship between
is for analytical purposes to derive an explicit relationship between










