Open Journal of Statistics
Vol.06 No.05(2016), Article ID:71413,16 pages
10.4236/ojs.2016.65073
Incorporating Uncertain Costs within a Series of Sequential Probability Ratio Tests
Conor McMeel, Brett Houlding*
Discipline of Statistics, Trinity College Dublin, Dublin, Ireland

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 20, 2016; Accepted: October 18, 2016; Published: October 21, 2016
ABSTRACT
We consider an extension to Sequential Probability Ratio Tests for when we have uncertain costs, but also opportunity to learn about these in an adaptive manner. In doing so we demonstrate the effects that allowing uncertainty has on observation cost, and the costs associated with Type I and Type II error. The value of information relating to modelled uncertainties is derived and the case of statistical dependence between the parameter affecting decision outcome and the parameter affecting unknown cost is also examined. Numerical examples of the derived theory are provided, along with a simulation comparing this adaptive learning framework to the classical one.
Keywords:
Adaptive Utility, Hypothesis Testing, Sequential Analysis, Sequential Probability Ratio Test

1. Introduction
Sequential Probability Ratio Tests (SPRTs) were introduced by Wald in 1945 [1] [2] as a sequential hypothesis test procedure for when data is considered in sequence rather than in entirety. They have been used in many fields of industry, for example: nuclear physics [3] , medicine [4] [5] , standardised testing [6] and radar detection [7] , to name just a few, and even though the classical theory has now been known for some seven decades, they are still the subject of research into extensions and generalisations [8] - [10] .
Generally, the objective of a SPRT is to balance the consequence of an error with the cost of acquiring further data and/or making additional observations, e.g. clinical trials, or stress tests. In this approach data is sought until the belief in the state of nature (namely the parameter controlling the decision outcome) is such that the expected cost of implementing the current optimal decision is less than that expected from seeking additional data, updating beliefs, and then implementing the (possibly different) optimal decision.
In its simplest form a SPRT consists of the following: A choice between two decisions or courses of action (here denoted 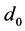 and
and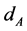 ), and a state of nature w that can take one of two possible values (
), and a state of nature w that can take one of two possible values ( or
or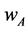 ). Depending on the decision that is selected and the true state of nature value, one of three possible losses may occur. Without loss of generality we assume a loss of
). Depending on the decision that is selected and the true state of nature value, one of three possible losses may occur. Without loss of generality we assume a loss of 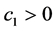 occurs if
occurs if 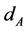 is selected when
is selected when 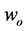 is true,
is true,  occurs if
occurs if  is selected but
is selected but  is true, and a loss of 0 otherwise (Table 1).
is true, and a loss of 0 otherwise (Table 1).
From the above it can be seen that the objective of the Decision Maker (DM) is to choose between  and
and  on the basis of their beliefs over the state of nature, seeking to match the decision to what they hope is its correct value. In general we denote such belief by the probability
on the basis of their beliefs over the state of nature, seeking to match the decision to what they hope is its correct value. In general we denote such belief by the probability  with
with . In this sense the losses
. In this sense the losses 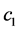 and
and 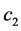 can be associated with what is commonly described as making a Type I or Type II error, and hence the connection to sequential hypothesis testing originally considered by Wald.
can be associated with what is commonly described as making a Type I or Type II error, and hence the connection to sequential hypothesis testing originally considered by Wald.
A graphic representation of this protocol is illustrated in Figure 1, where the x-axis varies over the possible value of  and the y-axis is the resulting expected loss incurred
and the y-axis is the resulting expected loss incurred
Table 1. Loss table applied within a SPRT.
Figure 1. An illustration of the losses involved within a SPRT. The x-axis varies over

by a particular strategy. The solid line represents the expected cost of implementing a decision immediately, whilst the curved dash line corresponds to the expected loss of implementing a decision only after taking some further data (at a cost)concerning the correct value of the state of nature. It is included as a curve as it can be shown that the expected loss of deciding after data collection is a concave function of 
For values of 







Figure 1 indicates, for the particular numerical example displayed, the range of values for 
Whilst the approach described above outlines the classical way of performing a SPRT, it fails to take into account that in practice, many of the costs involved will not be known for certain. For example, in the case of an observation cost, the cost associated with undertaking clinical trials prior to deciding to market a drug may not be known for sure, or in the case of a Type I or Type II error, the reputational or financial effect of implementing a poor decision may be unknown, e.g., releasing poorly coded software when there was opportunity to have more testing to determine unknown bugs. In such instances it is then natural for us to model our beliefs and uncertainties about relevant costs according to some parameter, say
The concept of unknown utility (utility defined to be negative loss), but which may instead be learned through experience, is the topic of adaptive utility theory first considered by Cyert and De Groot [11] . Here not only do we have uncertainty concerning decision outcome (as modelled through the unknown state of nature), but also in the preferences over those outcomes (or equivalently attitudes to risk) [12] - [14] .
In the case of only performing a solitary SPRT, and where the uncertainty relates to only the consequence of a Type I or Type II error, the appropriate procedure is equivalent to the classical one with the cost assigned to its expected value, as there is no possibility to learn about the relevant costs before implementing a decision. However, if the DM has opportunity to purchase information about such costs, e.g. by performing some market survey or enlisting the assistance of a knowledgeable expert, then the value that such information is worth may be calculated as the expected difference between the expected loss without the information, and the expected loss with it. Determining this value will be our primary interest [14] [15] :

Here I is the set of information statements we could receive, i is an actual information statement, D represents the set of available decisions, d a particular decision, and 
The remainder of this paper is as follows: In Section 2 we consider SPRTs with uncertain Type I or Type II error cost followed by uncertain observation cost in Section 3. In the former we consider the value of perfect information and that of noisy information, along with providing numerical examples. The details of a simulation carried out in the case of perfect information are also given. Finally we conclude in Section 4.
2. Unknown Consequence of Error
Suppose our uncertainty does not concern the cost of taking further observations, but rather the cost of a Type I or Type II error, or both (possibly with different distributions describing these). Without loss of generality assume the uncertainty is with respect the cost of a Type I error only. In this case our loss table is as in Table 2, where 
There are three steps to perform to generate the expected value of information relating to these uncertain costs. In the case of information being perfect then these are the following:
1) Consider a SPRT when no information is learned.
2) Obtain expected loss following learning of the uncertain parameter(s).
3) Subtract to obtain the expected value of information, which can then be subtracted from the unknown loss consequence(s).
In performing step 1 we utilize the expected costs using the loss in Table 3. Hence the expected loss on making an immediate decision, as a function of

If a Type I or Type II error is made, we learn the value of


Table 2. Loss table with uncertain cost of Type I error.
Table 3. Loss table assuming no learning about uncertain cost
Table 4. Loss table for numerical example in Section 2.1.
expected risk profile concerning how this may look depending on what is learned, based on the prior distribution of

2.1. Perfect Information Numerical Example
As a toy example illustrating this situation consider testing if a sequence of coins are fair (







The expected loss table is given in Table 4. From the description we see 


We may also consider sampling data by flipping a coin which is assumed to cost 0.1 units. We now calculate the range of 



The predictive probability of observing heads or tails, at any point, is:


Letting 

Now we can relate the bounds on 



Suppose

We also need to include the cost of flipping (0.1 units) resulting with an expected loss for observing once then deciding of



Observations should continue to be taken until 

With this risk profile we now compute the expected loss assuming we know the parameter



For

For

Recall the prior on 



Thus the expected value of perfect information is the difference between Equation (14) (without perfect information) and Equation (17) (with perfect information):

This represents the maximum amount of units we should be prepared to forsake in order to be informed the true value of the cost parameter 


Equation (19) represents the expected value of the loss of making a Type II error, but discounted by the fact that we obtain information which allows more informed decisions to be made in subsequent SPRTs. A plot of (19) is given in Figure 2 where it can be observed that local minima in the expected loss occur at boundaries of indifference between choices in the initial SPRT, and that plateaus in the expected loss coincide with values of 

2.2. Noisy Information
Now assume we only receive noisy observations concerning 
Denoting the true value of 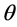


Figure 2. A plot of the expected loss incurred from committing a Type II error for Example 2.1 generated from Equation (19). The x-axis varies over the prior probability for the state of nature w, whilst the y-axis indicates the resulting expected loss.
means

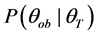



For each potential 






Once this has been generated the consequence of the error will be reduced in the risk table just as was the case with perfect information, allowing a classical SPRT to be performed.
2.3. Noisy Information Numerical Example
We return to the setting of Example 2.1, but now assume that the probability that the true value is observed is only 0.8, i.e.,


After observing a value for 


Letting 





Note that each term in the above implicitly depends on the initial value assigned to



As a result the expected value of noisy information 

Now the new expected cost of a Type II error 



Figure 3. A plot of the expected loss incurred from committing a Type II error for Example 2.3 generated from Equation (28). The x-axis varies over the prior probability for the state of nature w, whilst the y-axis indicates the resulting expected loss.
2.4. Numerical Simulation
Details of a numerical simulation are now provided. The scenario detailed in Example 2.1 was tested in R [16] by considering the outcome of 3 million trials of both the classic and adaptive framework.
Each classical trial consisted of:
1) A SPRT with consequence of Type I/II error of 2 and cost of observation 0.1 run repeatedly until a Type II error is made. The bounds used are those in Equation (14), namely
2) Upon making a Type II error, the cost from that particular SPRT is stored. The value of 
In accordance with our prior on


A further 3 million trials were then run using the adaptive framework under the same procedure but with the bounds in step 1 being different. This is due to the different values used for consequence of Type II error seen in Equation (19). Using initial values of 


The average costs are given in Table 5. As can be seen, this indicated a substantial improvement (21% with the numerical scenario here) in using the adaptive framework and formally taking such uncertainty into account.
2.5. Statistical Dependence
To conclude we give a brief discussion on the effect of their being statistical dependence between the state of nature w and cost parameter

Now consider the implementation of the SPRT. The initial loss table when w and 







Table 5. Average costs from the simulation described in Section 2.4.
Table 6. Assumed joint distribution between w and
Table 7. Implied conditional probabilities.
Table 8. Initial loss table in the case of independence.
Table 9. Loss table in the case of statistical dependence.
3. Unknown Observation Cost
Now suppose that the costs of making a Type I (



If we take the expected value of






where 







Here 

As the information i we may receive is currently unknown, we take the expectation of Equation (30). Subtracting this from Equation (29) (the expected risk without learning information) we obtain the expected value of that information, which can be thought of as the most we would be willing to pay for it in advance of seeing it. This should now be subtracted from

Remark. The expected value of information is zero for any 



Numerical Example
As a toy example to aid in clarification of the above, suppose we are testing the efficacy of a drug and are certain of the costs incurred in making a Type I or Type II error (say 2 and 4 units respectively). Assume, however, that we have little experience in running clinical trials (our observation costs) and are not sure if it will be easy and cheap to organise (


As we begin testing of the first drug we determine how to modify the SPRT procedure to take into account this uncertainty. Interest lies in the expected value of information of the observation cost, and we assume that the information will be of a perfect nature (namely remove all uncertainties). Noting that

So if 



For

For

Recalling the prior on 


Subtracting Equation (34) (expected risk with knowledge of

A plot of Equation (35) is provided in Figure 4. Note that the areas where the expected value of information is zero are where the decision rule is the same regardless of the information concerning the cost of sampling, agreeing with our earlier remark, and that the expected value of sampling information increases to be maximal where we are currently indifferent between making an immediate decision or taking further samples. With this to hand, we would continue by performing the SPRT as if we had an observation cost of

4. Conclusions
In this paper we have considered the generalisation of SPRTs from a classical to adaptive utility setting where preferences or associated costs are not assumed fully known but are instead learned through experience or by funding additional information through survey or trial etc. Both unknown cost of Type I/II error was examined before subsequently considering the effect of uncertain observation cost.
Both perfect and noisy information were discussed, where we demonstrated the methods of quantifying the value for such information and numerical examples were
Figure 4. A plot of the expected value of information in Example 3.1 given by Equation (35).
provided to demonstrate the theory. Statistical dependence between the parameter and the state of nature was also considered and shown to not influence results. The numerical simulation indicated the enhanced performance by formally treating uncertainties and opportunities to learn within a SPRT in comparison to the somewhat easier modelling assumption of equating uncertainties in costs to their expected values.
Cite this paper
McMeel, C. and Houlding, B. (2016) Incorporating Uncertain Costs within a Series of Sequential Probability Ratio Tests. Open Journal of Statistics, 6, 882-897. http://dx.doi.org/10.4236/ojs.2016.65073
References
- 1. Wald, A. (1945) Sequential Tests of Statistical Hypotheses. Annals of Mathematical Statistics, 16, 117-186.
http://dx.doi.org/10.1214/aoms/1177731118 - 2. Wald, A. and Wolfowitz, J. (1948) Optimum Character of the Sequential Probability Ratio Test. Annals of Mathematical Statistics, 19, 326-339.
http://dx.doi.org/10.1214/aoms/1177730197 - 3. Gross, K. and Humenik, K. (1991) Sequential Probability Ratio Test for Nuclear Plant Component Surveillance. Nuclear Technology, 93, 131-137.
- 4. Kulldorf, M., Davis, R.L., Kolczak, M., Lewis, E., Lieu, T. and Platt, R. (2011) A Maximised Sequential Probability Ratio Test for Drug and Vaccine Safety Surveillance. Sequential Analysis, 30, 58-70.
http://dx.doi.org/10.1080/07474946.2011.539924 - 5. Spiegelhalter, D., Grigg, O., Kinsman, R. and Treasure, T. (2003) Risk-Adjusted Sequential Probability Ratio Tests: Applications to Bristol, Shipman and Adult Cardiac Surgery. International Journal for Quality in Health Care, 15, 7-13.
http://dx.doi.org/10.1093/intqhc/15.1.7 - 6. Spray, J.A. and Reckase, M.D. (1996) Comparison of SPRT and Sequential Bayes Procedures for Classifying Examinees into two Categories using a Computerized Test. Journal of Educational and Behavioral Statistics, 21, 405-414.
http://dx.doi.org/10.3102/10769986021004405 - 7. Corsini, G., DalleMese, E., Marchetti, G. and Verrazzani, L. (1985) Design of the SPRT for Radar Target Detection. IEE Proceedings F Communications, Radar and Signal Processing, 132, 139-148.
http://dx.doi.org/10.1049/ip-f-1.1985.0035 - 8. Fay, M., Kim, H. and Hachey, M. (2007) On Using Truncated Sequential Probability Ratio Test Boundaries for Monte Carlo Implementation of Hypothesis Tests. Journal of Computational and Graphical Statistics, 16, 946-967.
http://dx.doi.org/10.1198/106186007X257025 - 9. Malladi, D. and Speyer, J. (1999) A Generalized Shiryayev Sequential Probability Ratio Test for Change Detection and Isolation. IEEE Transactions on Automatic Control, 44, 1522-1534.
http://dx.doi.org/10.1109/9.780416 - 10. Matas, J. and Chum, O. (2005) Randomized Ransac with Sequential Probability Ratio Test. Tenth IEEE International Conference on Computer Vision (ICCV’05), 1, 1727-1732.
http://dx.doi.org/10.1109/ICCV.2005.198 - 11. Cyert, R. and DeGroot, M. (1975) Adaptive Economic Models. Academic Press.
- 12. Boutilier, C. (2003) On the Foundations of Expected Expected Utility. Proceedings of the Eighteenth International Joint Conference on Artificial Intelligence (IJCAI-03), Acapulco, 9-15 August 2003, 285-290.
- 13. Chajewska, U., Koller, D. and Parr, R. (2000) Making Rational Decisions Using Adaptive Utility Elicitation. Proceedings of the Seventeenth National Conference on Artificial Intelligence and Twelfth Conference on Innovative Applications of Artificial Intelligence, Austin, Texas, 30 July-3 August 2000, 363-369.
- 14. Houlding, B. and Coolen, F.P.A. (2011) Adaptive Utility and Trial Aversion. Journal of Statistical Planning and Inference, 141, 734-747.
http://dx.doi.org/10.1016/j.jspi.2010.07.023 - 15. DeGroot, M. (1984) Changes in Utility as Information. Theory and Decision, 17, 287-303.
http://dx.doi.org/10.1007/BF00132613 - 16. R Core Team (2014) R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna.






