Received 26 April 2016; accepted 25 June 2016; published 28 June 2016

ABSTRACT

In several instances of statistical practice, it is not uncommon to use the same data for both model selection and inference, without taking account of the variability induced by model selection step. This is usually referred to as post-model selection inference. The shortcomings of such practice are widely recognized, finding a general solution is extremely challenging. We propose a model averaging alternative consisting on taking into account model selection probability and the likelihood in assigning the weights. The approach is applied to Bernoulli trials and outperforms Akaike weights model averaging and post-model selection estimators.

Keywords:

Model Selection, Post-Model Selection Estimator, Frequentist Model Averaging, Bernoulli Trials

1. Introduction

In statistical modeling practice, it is typical to ignore the variability of the model selection step, which can result in inaccurate post-selection inference (Berk et al. ( [1] [2] ), Belloni et al. ( [3] [4] ), Tibshirani et al. [5] , and Chernozhukov et al. [6] ). The model selection step is often a complex decision process and can involve collecting expert opinions, preprocessing, applying a variable selection rule, data-driven choice of one or more tuning parameters, among others. Except in simple cases, it is hard to explicitly characterize the form of the post-selection of interest while incorporating the variability of model selection. References for model selection include e.g. Zucchini [7] and Zucchini et al. [8] . An alternative to selecting a single model for estimation purposes is to use a weighted average of the estimates resulting from each of the models under consideration. This leads to the class of model averaging estimators. Model averaging can be done either in Bayesian and frequentist approaches. The most common Bayesian approach is Bayesian model averaging (BMA) and its variants, using Bayesian information criterion (BIC) as approximation (Schwarz [9] ). The seminal paper of Hoeting et al. [10] fully describes the basic of BMA. BMA and its applications can be found in Nguefack- Tsague ( [11] [12] ), Nguefack-Tsague and Ingo [13] , Nguefack-Tsague and Zucchini ( [14] [15] ). Several options are available for specifying the weights in frequentist approaches; references on least squares regression types and like include Hansen ( [16] - [21] ), Hansen and Racine [22] , Cheng and Hansen [23] , Charkhi et al. [24] , and Wan et al. [25] . The aforementioned weighting schemes perform model averaging on a set of nested candidate models with the weights vector chosen such that a specific criterion is minimized.

References using Akaike’s information criterion, AIC (Akaike [26] ) include Burnham and Anderson [27] , Nguefack-Zucchini [28] , Nguefack-Tsague ( [29] - [32] ). The R package [33] MuMIn is used to perform model averaging based on Burnham and Anderson [27] . Schomaker and Heumann [34] , and Schomaker [35] developes model averaging schemes based on multiple imputation and shrinkage; the R package MAMI is used for practical implementations. This paper is organized as follows: In Section 2, we develop model averaging based on information criterion while, in Section 3, we propose a new approach for computing the weights for the competing models, one that takes both account the selection probability and the likelihood of each model. Section 4 illustrates with applications to Bernoulli trials. The paper ends with concluding remarks.

2. Frequentist Model Averaging Based on Information Criterion

Let 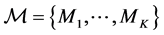be a set of K plausible models to estimate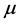, the quantity of interest. Denote by 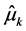the estimator of 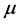obtained when using model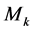. Model averaging involves finding non-negative weights, 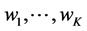, that sum to one, and then estimating 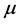by

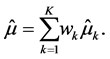(1)

In model selection, the model selection criterion determines which model is to be assigned weight one, i.e. which model is selected and subsequently used to estimate the parameter of interest. We note that, since the value of the selection criterion depends on the data, the index, 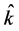, of the selected model is a random variable. We therefore denote the selected model by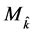, and the corresponding estimator of the quantity of interest, 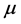, by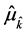. In terms of the notation introduced above, we may write

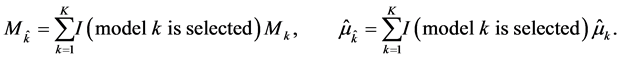
Clearly, the selected model depends on the set of candidate models, 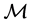, and on the selection procedure, which we denote by S. However, it is important to realize that, even if the same 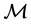and S, are used, different samples can lead to different models being selected; is a “randomly selected model”. In this section we focus attention on post-model selection estimators (PMSEs), which is the special case of model averaging estimators with zero/one weights only.

Some classical model averaging weights base the weights on penalized likelihood values. Let denote an “information criterion”of the form

(2)

where is a penalty term, and is the maximized likelihood value for the model. The Akaike infor- mation criterion (AIC, Akaike [26] ) is the special case with, where is the number of parameters of model. Buckland et al. [36] proposed using weights of the form:

(3)

“Akaike weights” (denoted by) refer to the case with. Numerous applications of Akaike weights are given in Burnham and Anderson [27] .

3. Likelihood and Selection Probability in Assigning the Weights

Since the selection procedure (S) and likelihood are important for model selection, we therefore suggest estimating by a weighted average of the in which the weights take account of S, specifically where they depend on estimators.

(4)

The likelihoods are taken into account because they quantify the relative plausibility of the data under each competing model; the estimated selection probability adjusts the weights for the selection pro- cedure. Both of these components are required. If one were to use only the likelihoods to determine the weights then complex models (i.e. models having many parameters) would automatically be assigned larger weights. The weights are similar to the weights defined in (3) but they differ in the way the likelihood is adjusted. With the proposed method a “bad” model will be penalized by any reasonable selection procedure through the probability, even if it is complex in terms of the number of parameters. We let the selection procedure determine in how far a model is penalized.

If the selection probabilities depend on some parameter for which a closed form expression exists, and if one can find an estimator of the parameter, then it is possible to obtain estimators for these probabilities.

4. Applications to Bernoulli Trials

Let be n independent Bernouilli trials, that is, is the number of successes;

Y-binomial (n, q), q unknown. Inference will be based on Y, since the likelihood function of the X_i’s is

and involves the sufficient statistic Y., is the proba-

bility mass function (PMF) of Y; the quantity of interest is. Sensitivity analyses showed that the finding obtained here are insensitive to parameter choice, irrespective of the sample size n.

4.1. A Two-Model Selection Problem

(a) Consider the choice between the 2 models: and. The true model may not belong to these 2 models. Suppose that the selection procedure chooses the model with smaller AIC. In this case, this entails to choosing the model with higher likelihood, since there is no parameter to be estimated for each model. will be chosen if or equivalently if.

Let and be the probabilities of choosing models 1 and 2, respectively.

where is the cumulative distribution function of binomial (n, q).

The estimated probabilities are given by, where and

. The PMSE if and otherwise. The properties of are given by

The Akaike weights are defined by

,.

The adjusted likelihood weights are defined by

,

.

The weighted estimators are

.

.

.

.

Figure 1 shows model selection probabilities for, and for the range of parameter space. The two curves cross at showing different values of the parameters space used for weighting.

Figure 2 compares PMSE to estimators based on Akaike weights and adjusted weights using true model selection probabilities. It can be seen that adjusted likelihood is always better than PMSE and Akaike weights estimators. However, for some values of the true parameter, the risk of Akaike weight tends to be slightly bigger than that of PMSEs. Maxima occur at while minima occur at 0.4 and 0.6.

(b) Consider now a choice between the following two models:

and.

AIC is used to select a model, , for illustration, we choose

.

Model 1 is chosen if

,.

and are obtained by replacing by.

The PMSE if and otherwise.

The Akaike weights are defined by

,

and the adjusted weights is defined by

,

.

Figure 3 displays model selection probabilities with both curves crossing at 0.6 and 0.4. At 0.5, while Model 2 is at the minimum, Model 1 is at maximum. Figure 4 displays risks performance of estimators. It can be seen that Akaike weighting does not perform better than PMSEs when the true parameter is between and between. However, the adjusted weights perform better than both.

4.2. Multi-Model Choice

Consider also a choice between the following models: for arbitrary K models; known. For a choice using AIC criterion, since there is no unknown parameter, this is the same as selecting the model with higher likelihood. Model is chosen if.

PMSE if is selected.

, if is chosen and 0 otherwise. Model selection probability for

model is given by:.

The estimated model selection probabilities are given by replacing by the estimated

. The Akaike weights are defined by, and the adjusted weights by

.

Numerical computations of the properties for these estimators are for, , models are between 0.1 and 0.9 and are given in Figure 5. One can see that Akaike weights are not better than PMSEs for certain

regions of the parameter space, but the adjusted likelihood weights are better than both.

5. Concluding Remarks

In this paper, we have considered model averaging in frequentist perspective; and proposed an approach of assigning weights to competing models taking account model selection probability and likelihood. The method appears to perform well for Bernoulli trials. The method needs to be applied in variety of situations before it can be adopted.

Acknowledgements

We Thank the Editor and the referee for their comments on earlier versions of this paper.

Cite this paper

Georges Nguefack-Tsague,Walter Zucchini,Siméon Fotso, (2016) Frequentist Model Averaging and Applications to Bernoulli Trials. Open Journal of Statistics,06,545-553. doi: 10.4236/ojs.2016.63046

References