Open Journal of Statistics
Vol.05 No.06(2015), Article ID:60836,12 pages
10.4236/ojs.2015.56063
Random Subspace Learning Approach to High-Dimensional Outliers Detection
Bohan Liu, Ernest Fokoué
School of Mathematical Sciences, Rochester Institute of Technology, Rochester, NY, USA
Email: bl3267@rit.edu, epfeqa@rit.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 September 2015; accepted 27 October 2015; published 30 October 2015
ABSTRACT
We introduce and develop a novel approach to outlier detection based on adaptation of random subspace learning. Our proposed method handles both high-dimension low-sample size and traditional low-dimensional high-sample size datasets. Essentially, we avoid the computational bottleneck of techniques like Minimum Covariance Determinant (MCD) by computing the needed determinants and associated measures in much lower dimensional subspaces. Both theoretical and computational development of our approach reveal that it is computationally more efficient than the regularized methods in high-dimensional low-sample size, and often competes favorably with existing methods as far as the percentage of correct outlier detection are concerned.
Keywords:
High-Dimensional, Robust, Outlier Detection, Contamination, Large p Small n, Random Subspace Method, Minimum Covariance Determinant

1. Introduction
We are given a dataset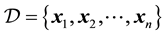 , where
, where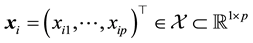 , under the special scenario in
, under the special scenario in
which  refers to as high dimensional low sample size (HDLSS) setting. It is assumed that the basic distribution of the
refers to as high dimensional low sample size (HDLSS) setting. It is assumed that the basic distribution of the ’sis multivariate Gaussian, so that the density of
’sis multivariate Gaussian, so that the density of  is given by
is given by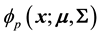 , with
, with
 . (1)
. (1)
It is also further assumed that the data set 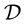 is contaminated, with a proportion
is contaminated, with a proportion 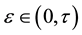 where
where , of observations that are outliers, so that under
, of observations that are outliers, so that under  -contamination regime, the probability density function of
-contamination regime, the probability density function of 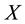 is given by
is given by
 , (2)
, (2)
where 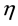 represents the contamination of the location parameter
represents the contamination of the location parameter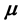 , while
, while 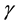 captures the level of contamination of the scatter matrix
captures the level of contamination of the scatter matrix

And experimenters of often addressing and tackling the outlier detection task in such situations using either the so-called Minimum Covariance Determinant (MCD) algorithm [1] or some extensions or adaptations thereof. The MCD is described as followed:
Minimum Covariance Determinant (MCD)
Step 1. Select h observations, and form the dataset

Step 2. Compute the empirical covariance 

Step 3. Compute the Mahalanobis distances
Step 4. Select the h observations having the smallest Mahalanobis distance;
Step 5. Update 

The MCD algorithm can be formulated as an optimization problem.

The MCD algorithm can be formulated as an optimization problem. The seminal MCD algorithm proposed by [1] , which is turned out to be rather slow and did not scale well as a function of the sample size n. That limitation of MCD leads its author to the creation of the so-called FAST-MCD [2] , focused on solving the outlier detection problem in a more computationally efficient way. Since the algorithm only needs to select a limited number h of observations for each loop, its complexity can be reduced when sample size n is large, since only a small fraction of the data is used. However, it must be noted that the bulk of the computations in MCD has to do with the estimation of determinants and the Mahalanobis distances, both requiring a complexity of 




where 
out that even the above Regularized MCD cannot be contemplated when

in such cases. The solution to that added difficulty is addressed by solving

where the regularized covariance matrix 

With






where 




From which the principal component scores 





2. Random Subspace Learning Approach to Outlier Detection
2.1. Rationale for Random Subspace Learning
We herein propose a technique that combines the concept underlying Random Subspace Learning (RSSL) by [14] with some of the key ideas behind minimum covariance determinant (MCD) to achieve a computational efficient, scalable, intuitive appealing and highly accurate outlier detection method for both HDLSS and LDHSS datasets. With our proposed method, the computation of the robust estimators of both location and scatter matrix can be achieved by tracing the optimal subspaces directly. Besides, we demonstrate via practical examples that our RSSL based method is computationally very efficient, specifically because it turns out that, unlike the other methods mentioned earlier, our method does not require the computationally expensive calculations of determinants and Mahalanobis distances at each step. Moreover, whenever such calculations are needed, they are all performed in very low dimensional spaces, further emphasizing the computational strength of our approach. The original MCD algorithm formulates the outlier detection problem as the problem of finding the smallest determinants of covariance computed from a sequence 




where m is the number of iterations needed for the MCD algorithm to converge. 


The number h of observations in each subset is required to be







2.2. Description Random Subspace Learning for Outlier Detection
Random Subspace Learning in its generic form is designed for precisely this kind of procedure. In a nutshell, RSSL combines instance-bagging (bootstrap i.e. sampling observations with replacement) with attribute-bag- ging (sampling indices of attributes without replacement), to allow efficient ensemble learning in high dimensional spaces. Random Subspace Learning (Attribute Bagging) proceeds very much like traditional bagging, with the added crucial step consisting of selecting a subset of the variables from the input space for training rather than building each base learners using all the p original variables.
Random Subspace Learning (RSSL): Attribute-bagging step
Step 1. Randomly draw the number 
Step 2. Draw without replacement the indices of d variables of the origina p variables;
Step 3. Perform learning/estimation in the d-dimensional subspace.
This attribute-bagging step is the main ingredient of our outlier detection approach in high dimensional spaces.
Random Subspace Outlier
Step 1. Draw with replacement


Step 2. Start for 
Draw without replacement from 

Drop unselected variables from 

Build the b th determinant of covariance
End for
Step 3. Sort the ensemble
Step 4. Form
Step 5. Compute 


We can build the robust distance by

The RSSL outlier detection algorithm computes a determinant of covariance for each subsample, with each subsample residing in a subspace spanned by the d randomly selected variables, where d is usually selected to be

along with the corresponding determinants. Then the best subsample, meaning the one with the smallest covariance determinant is singled. It turns out that in the LDHSS context



Random Subspace Learning for Outlier Detection when
Step 1. Draw with replacement


Step 2. Start for 
Draw without replacement from 

Drop unselected variables from 

Build the b th determinant of covariance
End for
Step 3. Sort the ensemble
Step 4. Keep the k smallest samples based on elbow to form


Step 5. Start for 
Select 

End for
Step 6. Form
Step 7. Compute 


We can build the robust distance by the same way:

Without selecting the smallest determinant of covariance, we choose to select a certain number of subsamples to achieve the variable selection through a sort of voting process. The portion of the most frequently appearing variables are elected to build an optimal space that allow us to compute our robust estimators. The simulation results and other details will be discussed later.
2.3. Justification Random Subspace Learning for Outlier Detection
Conjecture 1. Let 



Sketch 1. Let 


strapped sample from


present in

In other words, if 


have

Since 

sample




2.4. Alternatives to Parametric Outlier Detection Methods
The assumption of multivariate Gaussianity of the


subject to

using 

so that any 





OCSVM has been extensively studied and applied by many researchers among which [17] -[19] , and later enhanced by [20] . OCSVM is often applied to semi-supervised learning tasks where training focuses on all the positive examples (non-outliers) and then the detection of anomalies is performed by searching points that fall geometrically outside of the estimated/learned decision boundary of the good (non-outlying trained instances). It is a concrete and quite popular algorithm for solving one-class problems in fields like digital recognition and documentation categorization. However, it is crucial to note that OCSVM cannot be used with many other real life datasets for which outliers are not well-defined and/or for which there are no clearly identified all-positive training examples available such as gene expression mentioned before.
3. Computational Demonstrations
3.1. Setup of Computational Demonstration and Initial Results
In this section, we conduct a simulation study to assess the performance of our algorithm based on various important aspects of the data, and we also provide a comparison of the predictive/detection performance of our method against existing approaches. All our simulated data are generated according to the e-contami- nated multivariate Gaussian introduced via Equation (1) and Equation (2). In order to assess the effect the covariance between the attributes, we use an AR-type covariance matrix of the following form

where 




As can be seen in Figure 1, the overwhelming majority of samples lead to determinants that are small as evidenced by the heavy right skewness with concentration around zero. This further confirms our conjecture that as long as 
Figure 1. (left) Histogram of the distribution of the determinants from 
Since each bootstrapped sample selected has a small chance of being affected by the outliers, we can select the dimensionality that maximize this benefits. In our HDLSS simulations, determinants are computed based on all the randomly selected subspaces, and are ruled by predominantly small values, which imply the robustness of the classifier. Figure 1 patently shows the dominance of small values of determinants, which in this case are the determinants of all bootstrapped samples based on our simulated data. A distinguishable elbow is presented in Figure 2. The next crucial step lies in selecting a certain number of bootstrap samples, say k, to build an optimal subspace. Since most of the determinants are close to each other, it is a non-trivial problem, which means that k needs to be carefully chosen to avoid going beyond the elbow. However, it is important to notice if k is too small then the variable selection in later steps of the algorithm will become a random pick, because there is no opportunity for each variable to appear in the ensemble. Here, we choose k to be the number of roughly the first 30% to 80% of B bootstrap samples 






By Equation (20), it should be understood that we need to isolate the precious subsample 


3.2. Further Results and Computational Comparisons
As indicated in our introductory section, we use the Mahalanobis distance as our measure of proximity. As since we are operating under the assumption of multivariate normality, we use the traditional distribution quantiles


Figure 2. (left) Tail of sorted determinants in high dimensional
than 




where 
function used here is the basic zero-one loss defined by

It will be seen later that our proposed method produces predictive accurate outlier detection results, typically competing favorably against other techniques, and usually outperforming them. Firstly however, we show in Figure 3 the detection performance of our algorithm based on two randomly selected subspaces. The outliers detected by our algorithm are identified by red triangles and contained in the red contour, while the black circles are the normal data.
The improvement of our random subspace learning algorithm in low dimensional data with dimensionality such that 









Figure 3. (left) The outliers detected in a two dimensional subspace are marked as red triangles. Selection is based on
Figure 4. The average error and standard deviation in low dimensional simulation with 

Figure 5. The average error and standard deviation in high dimensional simulation with 

the absolute value of their kurtosis coefficients. This method is shown to yield good performances when dealing with small shift of mean and scatter of the covariance matrix. However, if the outliers lied on larger 




4. Conclusion
We have presented what we can rightfully claim to be a computational efficient, scalable, intuitive appealing and highly predictively accurate outlier detection method for both HDLSS and LDHSS datasets. As an adaptation of both random subspace learning and minimum covariance determinant, our proposed approach can be readily used on vast number of real life examples where both its component building blocks have been successfully applied. The particular appeal of the random subspace learning aspect of our method comes in handy for many outlier detection tasks on high dimension low sample size datasets like DNA Microarray Gene Expression datasets for which the MCD approach is proved to be computational untenable. As our computational demonstrations section above reveal, our proposed approach competes favorably with other existing methods, sometimes outperforming them predictively despite its straightforwardness and relatively simple implementation. Specifically, our proposed method is shown to be very competitive for both low dimensional space and high dimensional space outlier detection and is computationally very efficient. We are currently seeking out interesting real life datasets on which to apply our method. We also plan to extend our method beyond settings where the underlying distribution is Gaussian.
Acknowledgements
Ernest Fokoué wishes to express his heartfelt gratitude and infinite thanks to our lady of perpetual help for her ever-present support and guidance, especially for the uninterrupted flow of inspiration received through her most powerful intercession.
Cite this paper
BohanLiu,ErnestFokoué, (2015) Random Subspace Learning Approach to High-Dimensional Outliers Detection. Open Journal of Statistics,05,618-630. doi: 10.4236/ojs.2015.56063
References
- 1. Rousseeuw, P.J. (1984) Least Median of Squares Regression. Journal of the American Statistical Association, 79, 871-880.
http://dx.doi.org/10.1080/01621459.1984.10477105 - 2. Rousseeuw, P. and Van Driessen, K. (1999) A Fast Algorithm for the Minimum Covariance Determinant Estimator. Technometrics, 41, 212-223.
http://dx.doi.org/10.1080/00401706.1999.10485670 - 3. Filzmoser, P., Maronna, R. and Werner, M. (2008) Outlier Identification in High Dimensions. Computational Statistics & Data Analysis, 52, 1694-1711.
http://dx.doi.org/10.1016/j.csda.2007.05.018 - 4. Fritsch, V., Varoquaux, G., Thyreau, B., Poline, J.-B. and Thirion, B. (2011) Detecting Outlying Subjects in High-Dimensional Neuroimaging Datasets with Regularized Minimum Covariance Determinan 225. In: Fichtinger, G., Martel, A. and Peters, T., Eds., Medical Image Computing and Computer-Assisted Intervention MICCAI 2011, Springer, Berlin Heidelberg, 264-271.
- 5. Angiulli, F. and Pizzuti, C. (2002) Fast Outlier Detection in High Dimensional Spaces. In: Tapio, E., Heikki, M. and Hannu, T., Eds., Principles of Data Mining and 230 Knowledge Discovery, Springer, Rende, 15-27.
http://dx.doi.org/10.1007/3-540-45681-3_2 - 6. Aggarwal, C. and Yu, S. (2005) An Effective and Efficient Algorithm for High-Dimensional Outlier Detection. The VLDB Journal, 14, 211-221.
http://dx.doi.org/10.1007/s00778-004-0125-5 - 7. Ghoting, A., Parthasarathy, S. and Otey, M.E. (2008) Fast Mining of Distance-Based Outliers in High-Dimensional 235 Datasets. Data Mining and Knowledge Discovery, 16, 349-364.
http://dx.doi.org/10.1007/s10618-008-0093-2 - 8. Kriegel, H.-P., Kröger, P., Schubert, E. and Zimek, A. (2009) Outlier Detection in Axis-Parallel Subspaces of High Dimensional Data. In: Editor, Ed., Advances in Knowledge Discovery and Data Mining, Springer, München, 831-838.
http://dx.doi.org/10.1007/978-3-642-01307-2_86 - 9. Coppersmith, D. and Winograd, S. (1990) Matrix Multiplication via Arithmetic Progressions. Journal of Symbolic Computation, 9, 251-280.
http://dx.doi.org/10.1016/S0747-7171(08)80013-2 - 10. Le Gall, F. (2014) Powers of Tensors and Fast Matrix Multiplication. Proceedings of the 39th International Symposium on Symbolic and Algebraic Computation, New York, 23-25 July 2014. http://dx.doi.org/10.1145/2608628.2608664
- 11. Hubert, M. and Engelen, S. (2004) Robust PCA and Classification in Biosciences. Bioinformatics, 20, 1728-1736.
http://dx.doi.org/10.1093/bioinformatics/bth158 - 12. Croux, C. and Ruiz-Gazen, A. (1996) A Fast Algorithm for Robust Principal Components Based on Projection Pursuit. In: Prat, A., Ed., COMPSTAT, Springer, Heidelberg, 211-216.
http://dx.doi.org/10.1007/978-3-642-46992-3_22 - 13. Li, G.Y. and Chen, Z.L. (1985) Projection-Pursuit Approach to Robust Dispersion Matrices and Principal Components: Primary Theory. Journal of the American Statistical Association, 80, 759-766.
http://dx.doi.org/10.1080/01621459.1985.10478181 - 14. Ho, T.K. (1998) The Random Subspace Method for Constructing Decision Forests. IEEE Transactions on Pattern Analysis and Machine Intelligence, 20, 832-844.
http://dx.doi.org/10.1109/34.709601 - 15. Lopuhaa, H.P. and Rousseeuw, P.J. (1991) Breakdown Points of Affine Equivariant Estimators of Multivariate Location and Covariance. The Annals of Statistics, 19, 229-248.
http://dx.doi.org/10.1214/aos/1176347978 - 16. Schölkopf, B., Platt, J.C., Shawe-Taylor, J., Smola, A.J. and Williamson, R.C. (1999) Estimating the Support of a High-Dimensional Distribution. Neural Computation, 13, 1443-1471.
- 17. Hubert, M., Rousseeuw, P.J. and VandenBranden, K. (2005) Robpca: A New Approach to Robust Principal Component Analysis. Technometrics, 47, 64-79.
http://dx.doi.org/10.1198/004017004000000563 - 18. Manevitz, L.M. and Yousef, M. (2002) One-Class SVMs for Document Classification. The Journal of Machine Learning Research, 2, 139-154.
- 19. Zhang, R., Zhang, S., Muthuraman, S. and Jiang, J. (2007) One Class Support Vector Machine for Anomaly Detection in the Communication. Proceedings of the 5th Conference on Applied Electromagnetics, Wireless and Optical Communications, ELECTROSCIENCE’07, 14-16 December 2007, Tenerife, World Scientific and Engineering Academy and Society (WSEAS), Stevens Point, Wisconsin, 31-37.
- 20. Amer, M., Goldstein, M. and Abdennadher, S. (2013) Enhancing One-Class Support Vector Machines for Unsupervised Anomaly Detection. Proceedings of the ACM SIGKDD Workshop on Outlier Detection and Description, ODD’13, ACM, New York, 2013, 8-15.
http://dx.doi.org/10.1145/2500853.2500857











