Received 22 July 2015; accepted 11 September 2015; published 14 September 2015

ABSTRACT

We research the simultaneous approximation problem of the higher-order Hermite interpolation based on the zeros of the second Chebyshev polynomials under weighted Lp-norm. The estimation is sharp.

Keywords:

Hermite Interpolation Operator, Chebyshev Polynomial, Derivative Approximation

1. Introduction

For 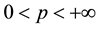and a non-negative measurable function u, the space 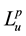is defined to be the set of measurable 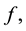such that

is finite. Of course, when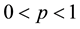, 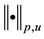is not a norm; nevertheless, we keep this notation for convenience.

For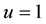, this is the usual 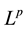space. For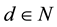, we write 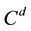for the space of functions that have dth continuous derivative on.

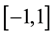We introduce a few notations. If 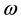is a Jacobi weight function, we write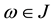. Let

. The Jacobi polynomials 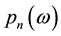are orthogonal polynomials with respect to the weight function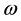, i.e.

It is well known that has distinct zeros in. These zeros are denoted by and the following order is assumed:

Later, when we fix, we shall write instead of.

For a given integer and, the Hermite interpolation is defined to be the unique polynomial of degree, denoted by, satisfying

for, where, if or then we have no interpolation at 1 or −1. We shall fix the integers and for the rest of the paper, and omit them from the notations. Thus, for example, we shall write instead of. Let

Vertesi and Xu [1] , Nevai and Xu [2] , and Pottinger considered the simultaneous approximation by Hermite interpolation operators.

We have researched the simultaneous approximation problem of the lower-order Hermite interpolation based on the zeros of Chebyshev polynomials under weighted Lp-norm in references [3] -[5] . We will research the simultaneous approximation problem of the higher-order Hermite interpolation in this article.

Let

be the zeros of, the nth degree Chebyshev polynomial of the second kind. For

, let be the polynomial of degree at most 3n − 1 which satisfies

Then the Hermite interpolation polynomial is given by

(1.1)

where

(1.2)

(1.3)

(1.4)

(1.5)

Theorem 1.

Let be defined as (1.1), for and, then we have

2. Some Lemmas

Lemmas 1. [6] Let be defined as (1.1), then

where, , is defined as function at before the commencement of the Taylor series of.

Lemma 2. [7]

If, then there exists a algebraic polynomial of degree at most such that

Let

be the zeros of, here, the nth degree Chebyshev polynomial of

the second kind. For, the well-known Lagrange interpolation polynomial of based on is given by

(2.1)

where

(2.2)

(2.3)

(2.4)

Lemma 3. [7] Let be defined as (2.4), for, and, we have

3. The Proof of Theorem 1

For, let be the polynomial of degree at most which satisfies Lemma 2. By the uniqueness of Hemite interpolation polynomial, it can be easily checked that,

(3.1)

We can conclude that

(3.2)

Firstly, we estimate. By (3.1), we have

(3.3)

Firstly, we estimate,

(3.4)

Let

(3.5)

be the polynomial of degree. By the uniqueness of Lagrange interpolation polynomial, it can be easily checked that,

(3.6)

By (3.5), (3.6) and Lemma 3, we can derive

(3.7)

Firstly, we estimate. Let

(3.8)

then

(3.9)

From Lemma 2 and (3.8), (3.9), we have that for

(3.10)

For, we have

(3.11)

We can conclude

(3.12)

Secondly, we estimate, and by Lemma 2, we get

(3.13)

Similarly

(3.14)

By (3.12), (3.13) and (3.14), we have

(3.15)

Similarly, we get

(3.16)

(3.17)

By (3.15), (3.16) and (3.17), we get

(3.18)

Similarly, we get

(3.19)

(3.20)

Secondly, we estimate, from Lemma 2,

(3.21)

From (3.2), (3.3), and (3.21), we can obtain the upper estimate

Funding

Hebei Science and Technology Research Universities Youth Fund project (QN20132001).

Cite this paper

XinWang,ChongHu,XiuxiuMa, (2015) The Approximation of Hermite Interpolation on the Weighted Mean Norm. American Journal of Computational Mathematics,05,387-392. doi: 10.4236/ajcm.2015.53033

References