World Journal of Nuclear Science and Technology
Vol.2 No.4(2012), Article ID:23808,6 pages DOI:10.4236/wjnst.2012.24031
Charge Fluctuations in pp and AA Collisions at RHIC and LHC Energies
1Department of Physics, Aligarh Muslim University, Aligarh, India
2Department of Applied Physics, Aligarh Muslim University, Aligarh, India
Email: Shakeel.Ahmad@cern.ch
Received April 20, 2012; revised May 26, 2012; accepted June 13, 2012
Keywords: Hadron-Hadron Collisions; Heavy-Ion Collisions; Charge Fluctuations
ABSTRACT
Various measures of event-by-event net charge and charge ratio fluctuations in pp and AA collisions at RHIC and LHC energies are studied using the different Monte Carlo generators: URQMD, HIJING and HIJING/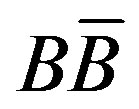 and the results are compared with the predictions for the independent emission, hadron gas and QGP phase. Values of the D-measures are observed to exhibit significant energy dependence for both pp and AA data. Furthermore, there is essentially no significant difference in the values of the D-measures predicted by the various Monte Carlo codes used in the present study. A slight centrality dependence of the D-measures in terms of net charge fluctuations is observed in the case of Au-Au data at 200 A GeV/c. These findings, thus, suggest that a difference in the D-measures for pp and AA collisions either the re-scattering effect plays a predominant role or there might be some new physics present in these collisions.
and the results are compared with the predictions for the independent emission, hadron gas and QGP phase. Values of the D-measures are observed to exhibit significant energy dependence for both pp and AA data. Furthermore, there is essentially no significant difference in the values of the D-measures predicted by the various Monte Carlo codes used in the present study. A slight centrality dependence of the D-measures in terms of net charge fluctuations is observed in the case of Au-Au data at 200 A GeV/c. These findings, thus, suggest that a difference in the D-measures for pp and AA collisions either the re-scattering effect plays a predominant role or there might be some new physics present in these collisions.
1. Introduction
Fluctuations measured in experiments, in general, depend on the property of the system under study and may contain important information about the system [1]. The interest in the studies involving event-by-event (ebe) fluctuations in hadronic (hh) and heavy ion AA collisions at relativistic energies is primarily connected to the idea that correlations and fluctuations of dynamical nature are believed to be associated with the critical phenomena of phase transition and leads to the local and global differences between the events produced under similar initial conditions [2]. Several different approaches [2-4] and ref. therein have been made to investigate the ebe fluctuations in hh and AA collisions at widely different energies, e.g., normalized factorial moments [5], multifractals [6,7], erracity [8,9], k-order rapidity spacing [10] and transverse momentum spectra [11]. Furthermore, fluctuations in the conserved quantities, like, electric charge, strangeness and baryonic numbers have emerged as new tools to estimate the degree of equilibration and criticality of the measured system [12]. The ebe electric charge fluctuations in hh and AA collisions have drawn considerable attention because;
1) QGP signature: A suppression in the net electric charge in the local phase has been theoretically predicted [13] as a signature of the plasma state. Such a decrease is expected as the charges are envisaged to be spread more evenly throughout the QGP volume than that in the hadronic gas.
2) Thermodynamic signature: An enhanced charge fluctuations has been observed [14] at RHIC and SPS energies, which might be due to anomalous proton number fluctuations at the critical point.
3) ρ and ω mesons: Charge fluctuations are influenced by the decay of hadronic resonances too. In the absence of QGP, the deviation of such fluctuations from the statistical behavior can be used to determine the abundance of ρ and ω mesons.
An attempt is, therefore made to carry out a systematic study of ebe charge fluctuations in pp and AA collisions by simulating the events using some of the popular Monte Carlo Generators (MCGs) which are based on the different physics pictures. Such studies may help establish the fluctuations as a robust variable and then to interpret the physical information contained in the measurement. Yet another advantage of the MCGs data is that the analysis could be carried out in both full and limited phase spaces, which in turn would lead to test the efficiencies of the detectors of limited acceptance [15].
2. Formalism
The charge fluctuations are generally studied in terms of two kind of measures [14,16]. The first one is the D-measure of the net charge fluctuations, the direct measure of which is the variance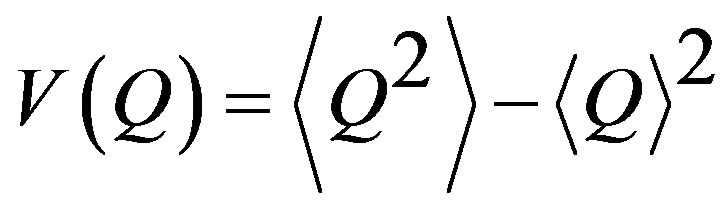 , where Q = n+ − n–; n+ (n–) being the multiplicities of positively (negatively) charged hadrons in a particular phase space of an event. The other measure is the charge ratio, R+ = n+ /n– and(or) R– = n–/n+. The D-measures of the charge ratio fluctuations are defined as
, where Q = n+ − n–; n+ (n–) being the multiplicities of positively (negatively) charged hadrons in a particular phase space of an event. The other measure is the charge ratio, R+ = n+ /n– and(or) R– = n–/n+. The D-measures of the charge ratio fluctuations are defined as , where
, where 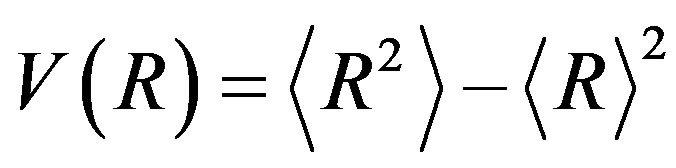 is the variance. In the high multiplicity limit, the above measures are neatly equal and are expressed as;
is the variance. In the high multiplicity limit, the above measures are neatly equal and are expressed as;
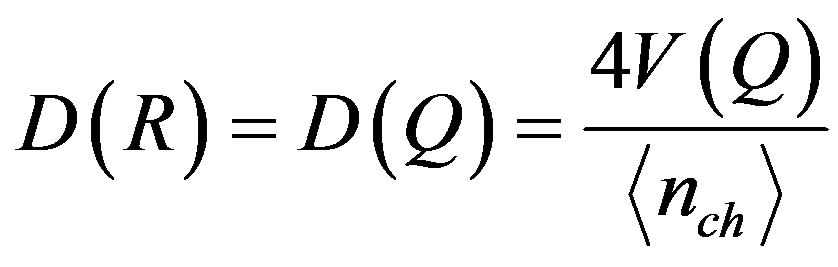 (1)
(1)
If each produced particle is assigned randomly a charge +1 or –1 with equal probability, then V(Q) =  and D(Q) = 4. in order to account for a non-zero net charge due to baryon stopping and the charge conservation in the large pseudorapidity, η window, two corrections are applied to the D-measure and the redefined parameter is given by[14,16,17]
and D(Q) = 4. in order to account for a non-zero net charge due to baryon stopping and the charge conservation in the large pseudorapidity, η window, two corrections are applied to the D-measure and the redefined parameter is given by[14,16,17]
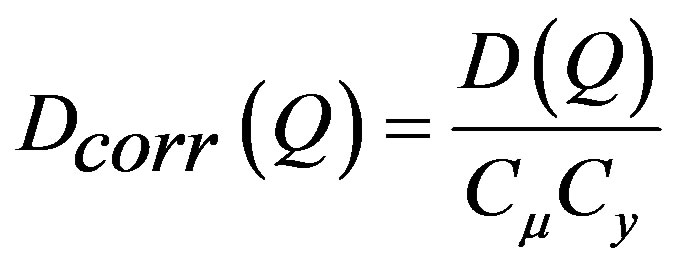 (2)
(2)
where, 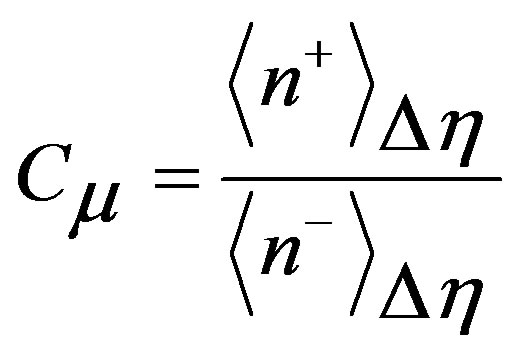 and
and 
It has been predicted that D(Q) = 1 for QGP, 2.9 for resonance gas 4 for uncorrelated pion gas [18-21].
3. Results and Discussion
3.1. Charge Fluctuations in pp Collisions
Values of D(Q), Dcorr(Q) and D(R±) are calculated in pp data in the incident energy range 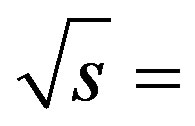 200 GeV to 14 TeV using the MCGs, HIJING-1.35 [22,23], HIJING/
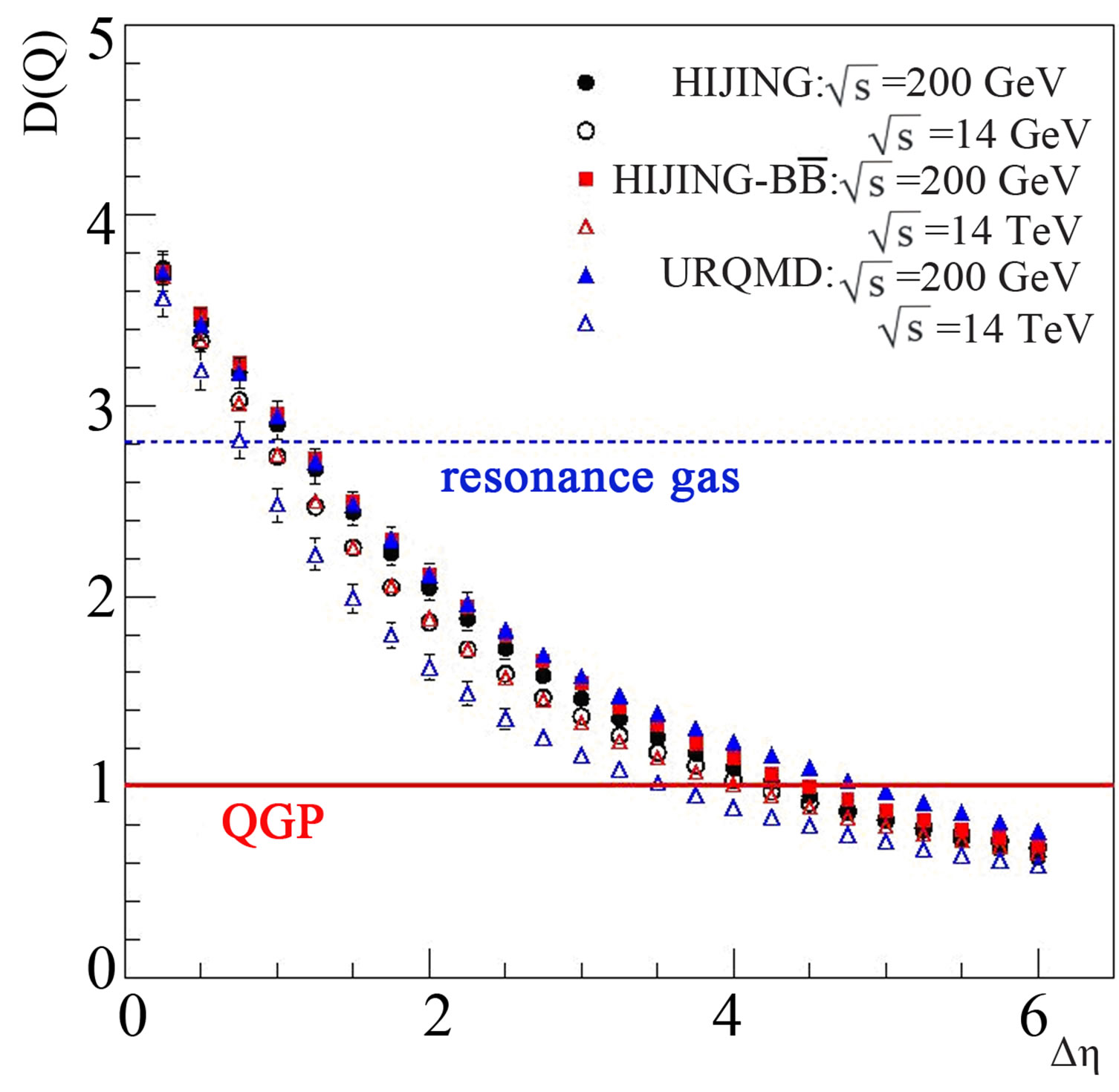
200 GeV to 14 TeV using the MCGs, HIJING-1.35 [22,23], HIJING/ 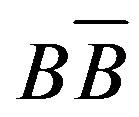 -1.10 [24] and URQMD-3.3p1 [25,26]. Each of these data samples consists of 105 events. Variations of D(Q) with the width of the pseudorapidity window, Δη for HIJING data samples at different incident energies are shown in Figure 1. Similar plots for the events generated by assigning the random charge is also shown in the same figure. For the purpose, all the charged particles of each event(taken from the 14 TeV sample) are randomly assigned a charge +1 or –1 with equal probabilities. It is noted from the figure that for this sample D(Q) values are ~ 4 irrespective of the fact that how small (or large) is the multiplicity in a chosen narrow (or wide) η-window. This result indicates that the ebe analysis may be successfully applied to the narrow phase space bins having a very limited number of particles [14]. The values of D(Q) for Δη ≤ 0.5, for all the data sets are found to be ~4, i.e. in the region of hadronic gas. These values, with the widening of η-window, decrease to ~1 and even below this value, i.e. the one expected for QGP.
-1.10 [24] and URQMD-3.3p1 [25,26]. Each of these data samples consists of 105 events. Variations of D(Q) with the width of the pseudorapidity window, Δη for HIJING data samples at different incident energies are shown in Figure 1. Similar plots for the events generated by assigning the random charge is also shown in the same figure. For the purpose, all the charged particles of each event(taken from the 14 TeV sample) are randomly assigned a charge +1 or –1 with equal probabilities. It is noted from the figure that for this sample D(Q) values are ~ 4 irrespective of the fact that how small (or large) is the multiplicity in a chosen narrow (or wide) η-window. This result indicates that the ebe analysis may be successfully applied to the narrow phase space bins having a very limited number of particles [14]. The values of D(Q) for Δη ≤ 0.5, for all the data sets are found to be ~4, i.e. in the region of hadronic gas. These values, with the widening of η-window, decrease to ~1 and even below this value, i.e. the one expected for QGP.
It is interesting to note that the data for different energies, i.e., from SPS, RHIC to LHC, overlap, suggesting that there is no energy dependence at all. Almost similar trend of variation of D(Q) with the size of the rapidity window has been observed [17] in the case of PYTHIA simulations of π+p collisions at 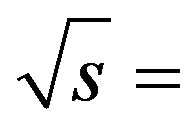 22 GeV. In order to compare the results from the three MCGs considered, D(Q) vs. Δη plots for the pp collisions at
22 GeV. In order to compare the results from the three MCGs considered, D(Q) vs. Δη plots for the pp collisions at 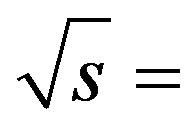 200 GeV and 14 TeV are shown in Figure 2. It may be noted from the figure that the URQMD data exhibit a slight energy dependence of D(Q), while the HIJING and HIJING/
200 GeV and 14 TeV are shown in Figure 2. It may be noted from the figure that the URQMD data exhibit a slight energy dependence of D(Q), while the HIJING and HIJING/ 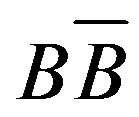 data show no such trends. After applying the corrections to the D(Q) values, as mentioned earlier, the values of D-measure, Dcorr(Q) are calculated and their dependence on the width of the η window are displayed in Figure 3 for the HIJING data. Comparison of the findings for different MCGs are shown in Figure 4. Following observations may be made from these figures:
data show no such trends. After applying the corrections to the D(Q) values, as mentioned earlier, the values of D-measure, Dcorr(Q) are calculated and their dependence on the width of the η window are displayed in Figure 3 for the HIJING data. Comparison of the findings for different MCGs are shown in Figure 4. Following observations may be made from these figures:

Figure 1. Variation of D(Q) and with the size of central window for the HIJING events.
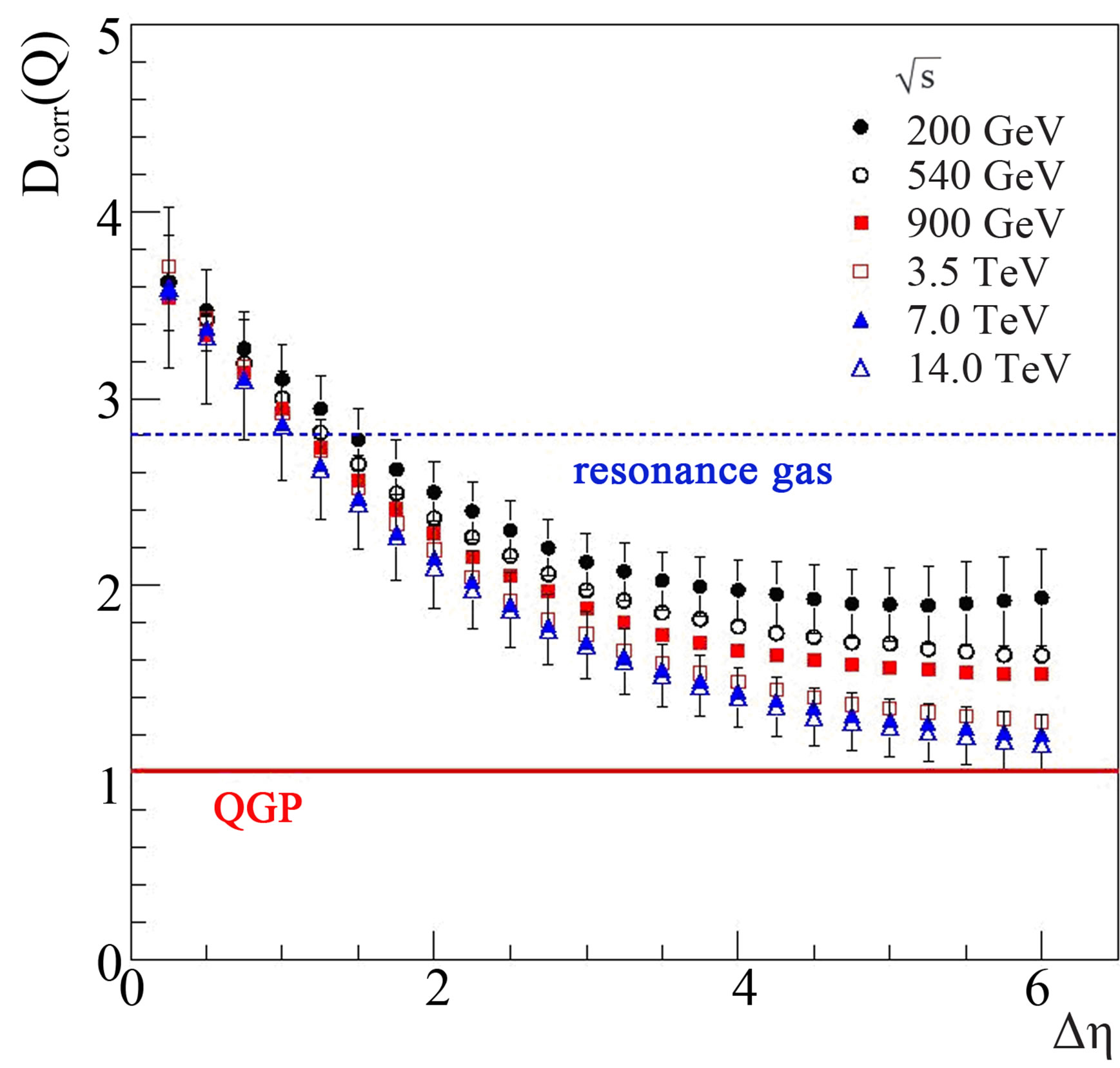
Figure 3. Dependence of Dcorr(Q) on Δη for the HIJING pp data at different energies.
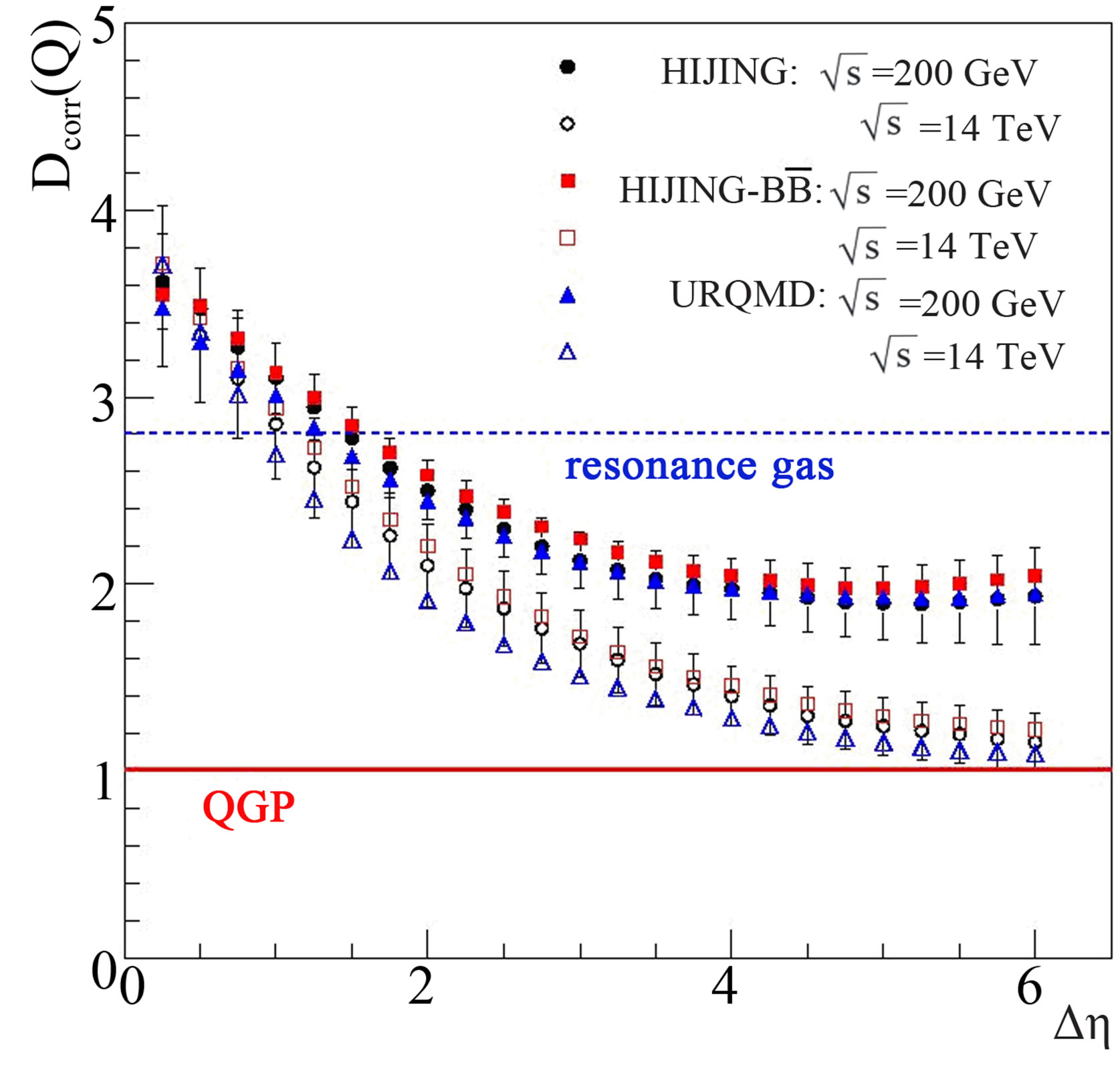
Figure 4. Dcorr(Q) vs Δη for the HIJING , HIJING/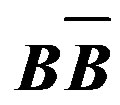 and URQMD pp data at
and URQMD pp data at 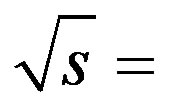 200 GeV and 14 TeV.
200 GeV and 14 TeV.
• For a small η window, D(Q) ~ Dcorr(Q) ~ 4. However, the Dcorr(Q) values decrease to a little above 1 and thereafter tend to acquire a saturation in the larger η windows. This indicates that the influence of global charge conservation and leading particle stopping is well taken into account by the corrected measure, Dcorr(Q).
• Dcorr(Q) values, for a given Δη are found to decrease with energy and becomes more pronounced in the saturation region of Δη. Such dependence might be due to the increasing number of charged particles at higher energies rather larger charge asymmetry.
• Values of D-measures as obtained for the three MCGs are nearly the same.
Saturations in the Dcorr(Q) values are observed for the pseudorapidity windows, Δη ≥ 4. However, the correction factor,
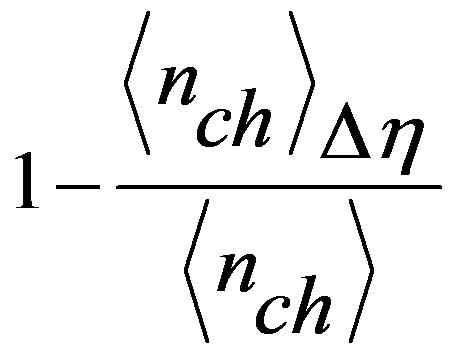 ~ 0 for the entire kinematic phase space and hence can not be used for the larger η windows [15]. The results, therefore corresponding to Δη ~ 4 and beyond, presented in Figures 3 and 4 should be overlooked. The values of Dcorr(Q) for a smaller η window are observed to be much larger than 1, which is expected because of the fact that if the η-bin width is small enough, it will not pick up all the particles decaying from a resonance [15]. Due to the presence of positively charged particles in the initial state, average number of positively charged particles in a particular η-window will be larger than that of negatively charged particles. This charge asymmetry becomes more pronounced with the widening of the η-windows. Leading to the fluctuations in the charge ratio, R+ = n+/n– and R– = n–/n+ and that it is not a simple inverse relation. D-measures in terms of charge ratio, R+ and R- have been estimated and their variations with Δη is presented in Figure 5; events with n± = 0 have been excluded while evaluating D(R+) and D(R–) are found to depend on incident energy such that for a given Δη, values of both the measures are larger at higher energies. These values lie in the region of hadron gas and above for the Δη range ~1 - 4. It has been reported [14,16] that for π+-p and k+-p collisions at 250 GeV, the values of D(R+) are larger than that of D(R–). However in the present study, values of both the parameters are found to have almost similar values except for the HIJING data sample for which D(R+) values are somewhat smaller than the corresponding D(R–) values.
~ 0 for the entire kinematic phase space and hence can not be used for the larger η windows [15]. The results, therefore corresponding to Δη ~ 4 and beyond, presented in Figures 3 and 4 should be overlooked. The values of Dcorr(Q) for a smaller η window are observed to be much larger than 1, which is expected because of the fact that if the η-bin width is small enough, it will not pick up all the particles decaying from a resonance [15]. Due to the presence of positively charged particles in the initial state, average number of positively charged particles in a particular η-window will be larger than that of negatively charged particles. This charge asymmetry becomes more pronounced with the widening of the η-windows. Leading to the fluctuations in the charge ratio, R+ = n+/n– and R– = n–/n+ and that it is not a simple inverse relation. D-measures in terms of charge ratio, R+ and R- have been estimated and their variations with Δη is presented in Figure 5; events with n± = 0 have been excluded while evaluating D(R+) and D(R–) are found to depend on incident energy such that for a given Δη, values of both the measures are larger at higher energies. These values lie in the region of hadron gas and above for the Δη range ~1 - 4. It has been reported [14,16] that for π+-p and k+-p collisions at 250 GeV, the values of D(R+) are larger than that of D(R–). However in the present study, values of both the parameters are found to have almost similar values except for the HIJING data sample for which D(R+) values are somewhat smaller than the corresponding D(R–) values.
It has been observed [14] that both D(Q) and D(R±) exhibit almost similar multiplicity dependence in the region, Δη ≤ 2 irrespective of the fact that whether the multiplicity in chosen η window is even or odd. However, for a wider η-window, Δη ≤ 3, D(Q) exhibits almost equal separation for the even and odd multiplicities. PHENIX collaboration [13,27], on the other hand has observed that D(R) depends on the multiplicity while D(Q) does not. Study of the multiplicity dependence of D-measures by analyzing the data sets considered in the present study may lead one to make the remark that whether both D(Q) and D(R) are equally good measures in recording the changes in charge fluctuations with multiplicity in different central rapidity windows.
3.2. Charge Fluctuations in AA Collisions
According to the participant model [28], average total charge Q of AA collisions is related to the charge produced in nucleon-nucleon (nn) collisions, Qi as,
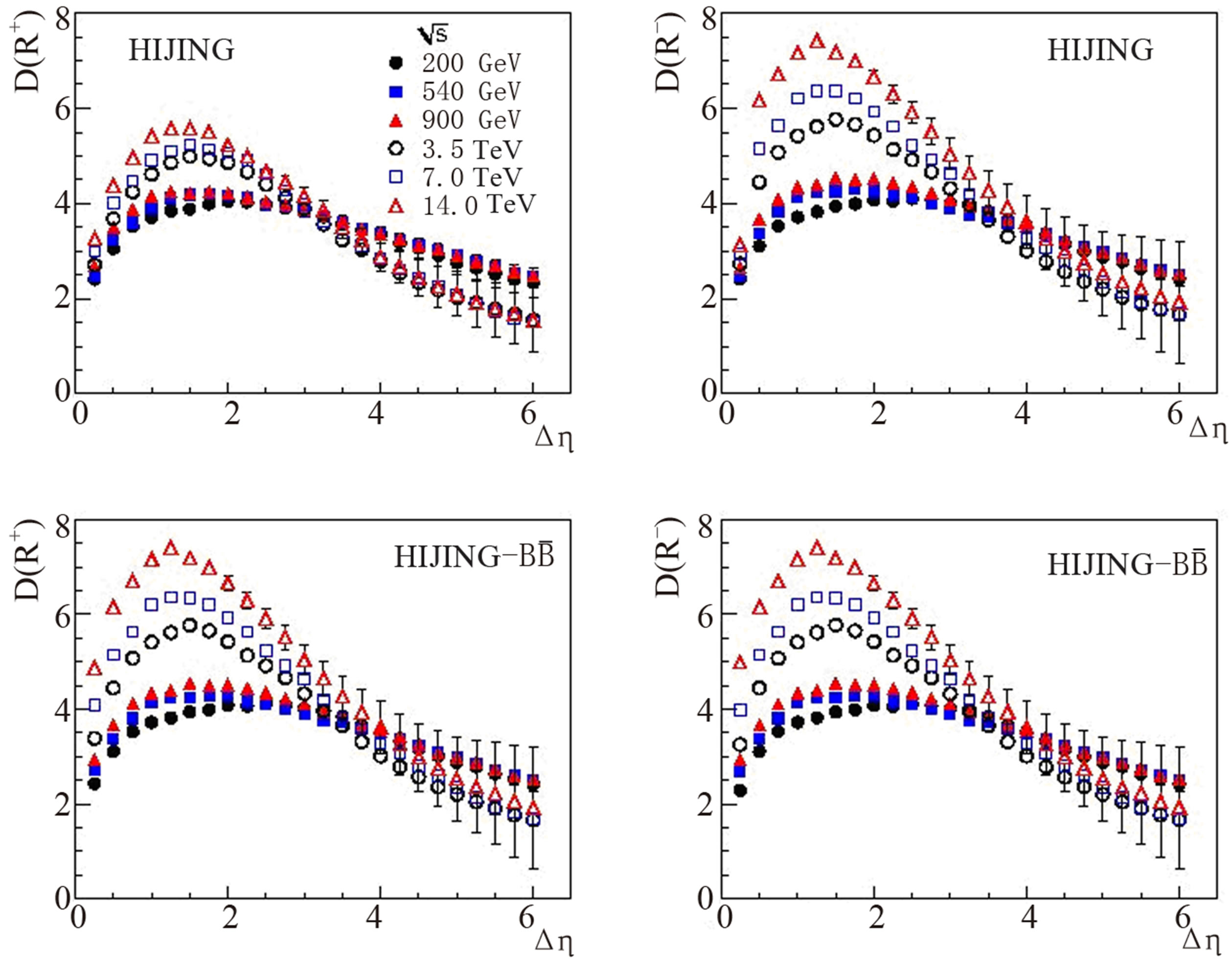
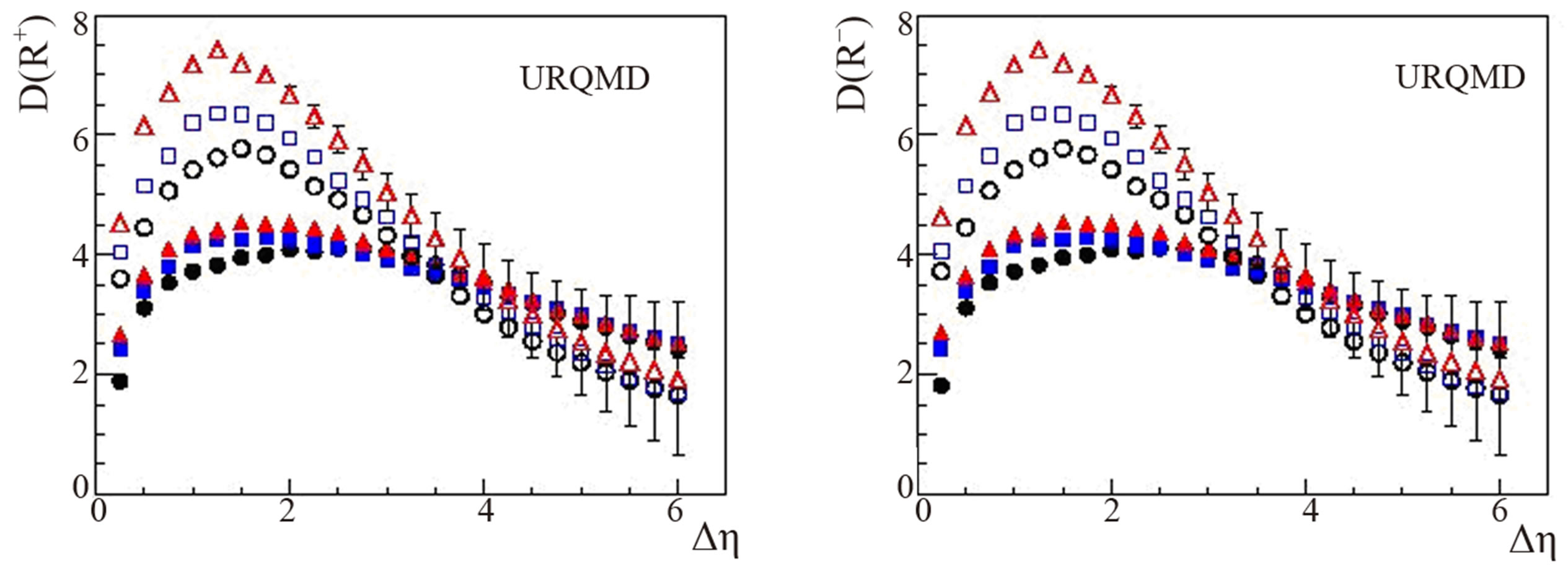
Figure 5. Variations of D(R+) and D(R+) with Δη for the HIJING, HIJING/  and URQMD pp data at different energies.
and URQMD pp data at different energies.
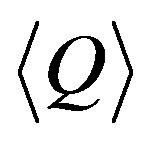 = NpQi, where Np is the total number of nn collisions while the quantities in angular brackets denote the averaged values over the event sample. The model predicts [15,28] that if re-scattering effects are neglected, D-measures for pp and AA collisions should acquire almost identical values. D-measures for pp and AA data simulated using different MCGs have been observed [15] to acquire nearly similar values with the re-scattering switched off, if the event generator takes it into account, e.g., VNIb and RQMD. In order to test the predictions with the participant model at LHC energies and compare the findings with the SPS and RHIC energy data, values of Dcorr(Q) are plotted against Δη for the HIJING data sets corresponding to pp and AA collisions at RHIC and LHC energies. These variations are shown in Figure 6. It may be noted in the figure that D-measure for pp and Au-Au collisions at
= NpQi, where Np is the total number of nn collisions while the quantities in angular brackets denote the averaged values over the event sample. The model predicts [15,28] that if re-scattering effects are neglected, D-measures for pp and AA collisions should acquire almost identical values. D-measures for pp and AA data simulated using different MCGs have been observed [15] to acquire nearly similar values with the re-scattering switched off, if the event generator takes it into account, e.g., VNIb and RQMD. In order to test the predictions with the participant model at LHC energies and compare the findings with the SPS and RHIC energy data, values of Dcorr(Q) are plotted against Δη for the HIJING data sets corresponding to pp and AA collisions at RHIC and LHC energies. These variations are shown in Figure 6. It may be noted in the figure that D-measure for pp and Au-Au collisions at 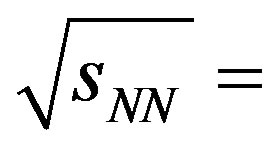 200 GeV are nearly the same at least in the region of Δη < 4. This result incidenttally, agrees fairly well with the one reported by PHENIX collaboration [13,27]. However, in the present study, the values of D-measure for the pp data are found to acquire relatively smaller values as compared to those obtained for the AA data. Fluctuations in the Dcorr(Q) values corresponding to Pb-Pb data, as can be seen in the figure are due to the limited statistics. These findings, thus, reveal that the D-measures for both pp and AA exhibit significant energy dependence. These observations are, thus, in agreement with the idea [6,7] that at lower energies, a single nn collision is dominated by hadronic picture, whereas, at higher energies, such collision can experience the contents of nucleons, i.e., at higher energies gluons are expected to make larger contributions which would cause a decrease in the D(Q) values with increasing incident energies.
200 GeV are nearly the same at least in the region of Δη < 4. This result incidenttally, agrees fairly well with the one reported by PHENIX collaboration [13,27]. However, in the present study, the values of D-measure for the pp data are found to acquire relatively smaller values as compared to those obtained for the AA data. Fluctuations in the Dcorr(Q) values corresponding to Pb-Pb data, as can be seen in the figure are due to the limited statistics. These findings, thus, reveal that the D-measures for both pp and AA exhibit significant energy dependence. These observations are, thus, in agreement with the idea [6,7] that at lower energies, a single nn collision is dominated by hadronic picture, whereas, at higher energies, such collision can experience the contents of nucleons, i.e., at higher energies gluons are expected to make larger contributions which would cause a decrease in the D(Q) values with increasing incident energies.
Impact parameter, b dependence of D-measure is examined by plotting the variations of Dcorr(Q) with b for Pb-Pb collisions at 5.5A TeV. These results are shown in Figure 7. Data points for each of the two central η-windows are from the five sets of HIJING events, each generated for a different impact parameter range, e.g. b = 0 - 1 fm, 1 - 2 fm, etc. It may be noticed in the figure that the data points for both the η windows lie below the resonance gas and above that the one expected for a QGP. A slight centrality dependence may also be noticed such that the
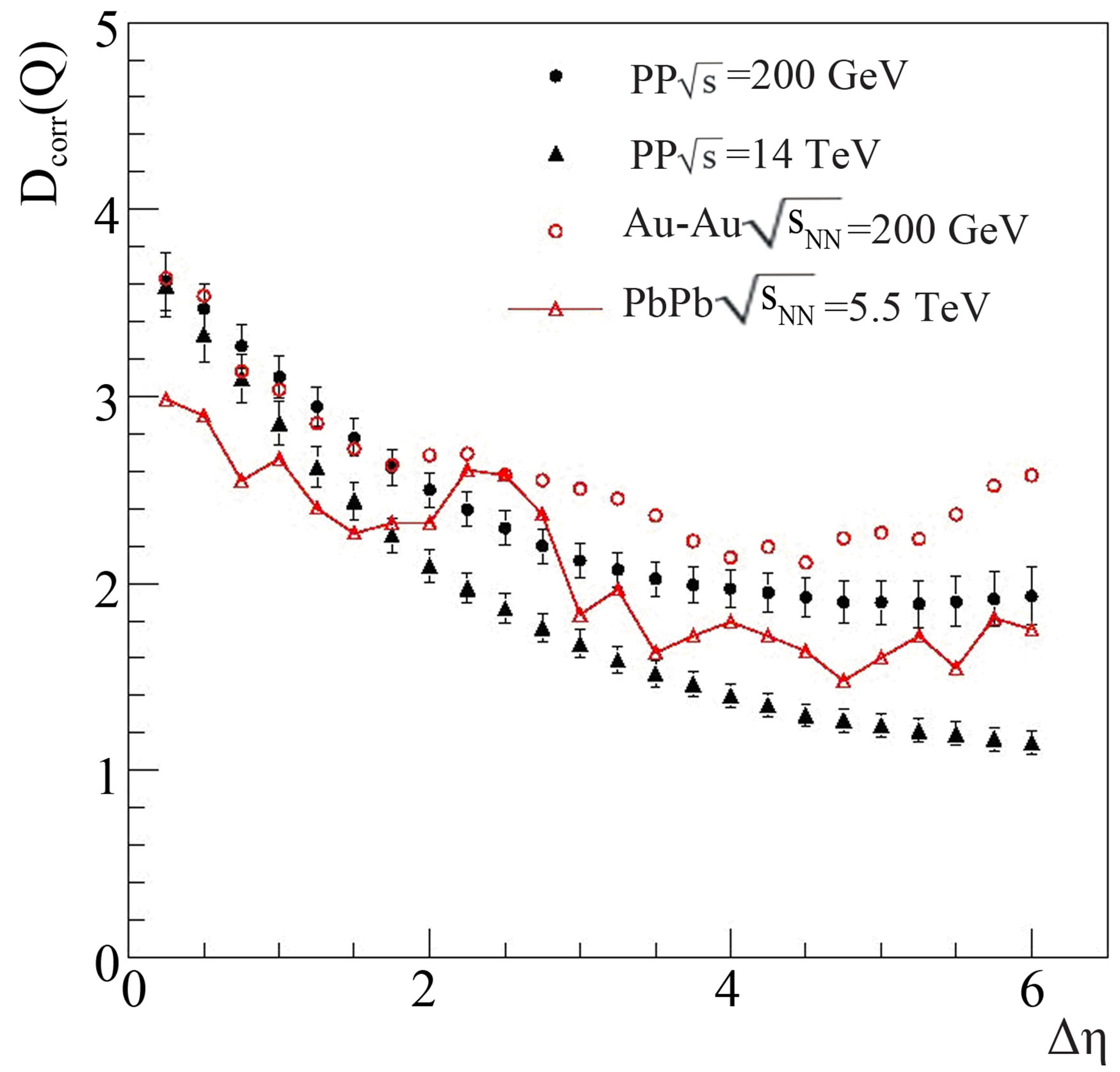
Figure 6. Dependence Dcorr(Q) on Δη for the HIJING. Simulated events corresponding to pp and AA collisions at RHIC and LHC energies.
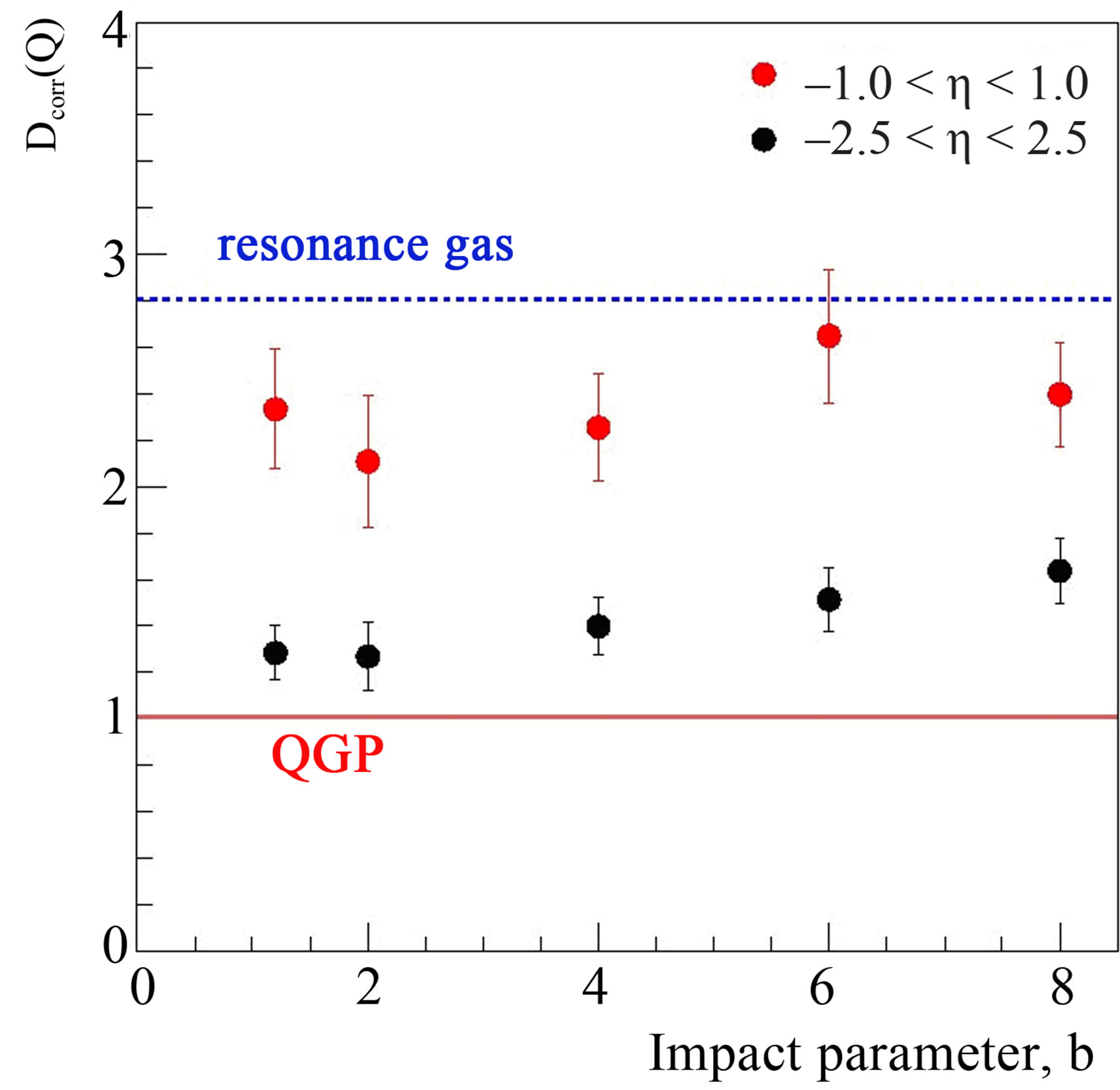
Figure 7. Dependence Dcorr(Q) on impact parameter for the HIJING simulated events corresponding to 5.5 A TeV. Pb-Pb collisions.
Dcorr(Q) increases with increasing centrality. It should be mentioned here that the D-measure observed in the present study, are relatively smaller as compared to those reported for Au-Au collisions at RHIC energies [13,14,27]. This difference in the D-measures might be due to the difference in gluon populations at RHIC and LHC energies.
4. Conclusions
On the basis of the findings of the present work the following conclusions may be drawn:
1) D-measures, after the correction, are found to exhibit significant energy dependence for both pp and AA data for all the three MCGs.
2) D-measure in terms of the net charge fluctuations may be regarded as a better parameter for assessing the change in the charge fluctuations as compared to the Dmeasures of the charge ratio fluctuations.
3) There is no essential difference in the values of D-measures predicted by the different theoretical models considered in the present study, e.g., HIJING-1.35, HIJING/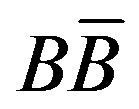 -1.10 and URQMD-3.1p.
-1.10 and URQMD-3.1p.
4) The observed energy dependence of the D-measure for pp collisions indicate that at higher energies gluons have higher contribution and reduced the values of the D-measures. D-measures for AA collisions also exhibit a similar trend of variation with the incident energy as the observed due to pp collisions.
It may be remarked that charge fluctuations are sensitive to the parton number embedded in different theoretical models, if the re-scattering effects are not essential and hence the D-measures may be regarded as a signature of QGP. Larger values of the D-measures for AA collisions as compared to those for pp collisions, if observed at LHC energies, would indicate that a stronger re-scattering effect is present in AA collisions. A smaller D(Q) values for AA collisions in comparison to pp collisions, on the other hand, if observed, would lead to search of some new physics in future heavy-ion experiments.
REFERENCES
- M. Dooring and V. Koch, nucl-th/0204009.
- E. De, A. Wolf, et al., Physics Reports, Vol. 27, 1996, p. 236.
- S. Ahmad, Journal of Physics G, Vol. 30, 2004, p. 1.
- M. M. Khan, et al., Analysis beyond Intermittency in Multiparticle Production in Relativistic Nuclear Collisions,” International Journal of Modern Physics E, Vol. 19, No. 11, 2010, p. 2219. doi:10.1142/S0218301310016612
- A. Bialas and R. Peschanski, “Moments of Rapidity Distributions as a Measure of Short-Range Fluctuations in High-Energy Collisions,” Nuclear Physics B, Vol. 273, No. 3-4, 1986, pp. 703-718. doi:10.1016/0550-3213(86)90386-X
- R. C. Hwa, “Fractal Measures in Multiparticle Production,” Physical Review D, Vol. 41, No. 5, 1990, pp. 1456-1462.
- S. Ahmad, et al., Chaos, Solitons & Fractals, Vol. 42, 2009, p. 538. doi:10.1103/PhysRevD.41.1456
- R. C. Hwa, Acta Physica Polonica B, Vol. 27, 1996, p. 1789.
- F. Liu, et al., Physics Letters B, Vol. 516, 2001, p. 293.
- M. L. Cherry, et al., Acta Physica Polonica B, Vol. 29, 1998, p. 2129.
- J. C. Rider, et al., Nuclear Physics A, Vol. 698, 2002, p. 611c.
- Q. J. Liu and T. A. Trainor, hep-ph/0301214.
- K. Adox, et al., “PHENIX col.,” Physical Review Letters, Vol. 89, 2001, Article ID: 082301.
- M. R. Atayan et al., Physical Review D, Vol. 71, 2005, Article ID: 012002.
- Y. F. Wu and Z. M. Li, Acta Physica Polonica B, Vol. 35, 2004, p. 289.
- Q. H. Zhang, et al., hep-ph/0202057.
- A. Feng, et al., International Journal of Modern Physics A, Vol. 22, 2007, p. 2909.
- V. Koch, et al., Nuclear Physics A, Vol. 698, 2002, p. 261.
- S. Jeon and V. Koch, Physical Review Letters, Vol. 85, 2000, p. 2076.
- M. Asakawa, et al., Physical Review, Vol. 85, 2000, p. 2072.
- V. M. Martinis, nucl-th/0412007.
- X. N. Wang, Physics Reports, Vol. 280, 1997, p. 287.
- X. N. Wang and M. Gyulassy, Computer Physics Communications, Vol. 83, 1994, p. 307.
- S. E. Vance and M. Gyulassy, Physical Review Letters, Vol. 83, 1999, p. 1735.
- S. A. Bass, et al., Progress in Particle and Nuclear Physics, Vol. 41, 1998, p. 225.
- M. Bleicher, et al., Journal of Physics G, Vol. 25, 1999, p. 1859.
- J. Nystrand, nucl-ex/0209019.
- G. Baym and H. Heiselberg, Physics Letters B, Vol. 469, 1999, p. 7.