American Journal of Operations Research
Vol. 2 No. 2 (2012) , Article ID: 19952 , 7 pages DOI:10.4236/ajor.2012.22030
Application of the p-Median Problem in School Allocation
Laboratory of Mathematics of Decision and Numerical Analysis, Cheikh Anta Diop University, Dakar, Senegal
Email: fagueyens@yahoo.fr, babacarm.ndiaye_idrissa.ly@ucad.edu.sn
Received April 18, 2012; revised May 20, 2012; accepted May 31, 2012
Keywords: Non-Convex Optimization; Location Models; School Allocation
ABSTRACT
This paper focus on solving the problem of optimizing students’ orientation. After four years spent in secondary school, pupils take exams and are assigned to the high school. The main difficulty of Education Department Inspection (EDI) of Dakar lies in the allocation of pupils in the suburbs. In this paper we propose an allocation model using the p-median problem. The model takes into account the distance of the standards imposed by international organizations between pupil’s home and school. The p-median problem is a location-allocation problem that takes into account the average (total) distance between demand points (pupil’s home) and facility (pupil’s school). The p-median problem is used to determine the best location to place a limited number of schools. The model has been enhanced and applied to a wide range of school location problems in suburbs. After collecting necessary numerical data to each EDI, a formulation is presented and computational results are carried out.
1. Introduction
Every year, the Education Department Inspection (EDI) of Dakar has difficulties for assigning pupils to high schools of the suburbs. After four years spent in secondary school, pupils take exams and are assigned to high schools. The EDI of Dakar must take several important decisions such as network design, pupil assignments, construction of new high schools, etc. Nowadays, due to the fact that the number of pupils increases each year, problems related to pupil assignments have become so complex that rudimentary techniques seam unsuitable. Thus, the need to use analytical tools to deal locationallocation problems has come out to the attention of EDI decision makers. With some processing techniques, we solve instances for the EDI of Guediewaye, Thiaroye and Keur Massar to find the optimal configuration, to install new high schools in order to attend the demand of a population. It is possible to build a high school inside some colleges that have space or in sites (vacant land) of the area. Location-allocation problems deal with decisions of finding the best (or optimal) configuration for the installation of one or more facilities in order to attend the demand of a population [1].
Nooradelena and Noraida [2] used the p-median problem to determine the best location to place a limited number of emergency medical services taking into account the uncertainty in the demand for the emergency services. The p-median problem is a location-allocation problem that has been extensively studied. The reason for the interest in the p-median problem is that it has practical applications in a wide variety of planning problems: locating telephone switching centers [3], school districting [4], and bank location [5]. Chardaire and Lutton [6] extended the p-median problem to account for different types of located facilities that interact such as telecommunication terminals that are connected to concentrators, which are connected to each other. Densham and Rushton [7] worked on a p-median problem where every facility needs a minimum workload.
In this paper, the school location for pupils from secondary school to high school is presented. An allocation model using the p-median problem is proposed. More details concerning the p-median problem formulation can be found in Church and ReVelle [8]. We solve the mixedinteger 0 - 1 linear program using the IBM-CPLEX’s MILP solver [9]; and show how the simulation techniques can be applied successfully to practical decision support of Dakar’s EDIs. For each EDI in Dakar: Guediewaye, Thiaroye and Keur Massar, all schools (or demand points) are listed, with  the number of pupils who pass exam in each school with
the number of pupils who pass exam in each school with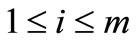 . Selected colleges will be expanded into high schools and free surfaces are built for high schools. Facilities or facility locations are places that are suitable to establish schools (service facilities). Service facilities cannot be erected outside facility locations. A configuration is a set of usually p candidates that are proposed to get a service facility. However, during the optimization process the configuration might consist of a different number. Every configuration that has exactly p facilities is a solution for the p-median problem. The integer number p must be chosen to specify how many facilities are to be located. The optimal solution is a configuration that has the minimal distance. The objective function is the total distance from every point of demand to the closest facility of the configuration. The distance is weighted or multiplied by the population of the site.
. Selected colleges will be expanded into high schools and free surfaces are built for high schools. Facilities or facility locations are places that are suitable to establish schools (service facilities). Service facilities cannot be erected outside facility locations. A configuration is a set of usually p candidates that are proposed to get a service facility. However, during the optimization process the configuration might consist of a different number. Every configuration that has exactly p facilities is a solution for the p-median problem. The integer number p must be chosen to specify how many facilities are to be located. The optimal solution is a configuration that has the minimal distance. The objective function is the total distance from every point of demand to the closest facility of the configuration. The distance is weighted or multiplied by the population of the site.
The paper is organized as follows: In Section 2, we present the allocation model using the p-median problem formulation. Section 3 is devoted to the numerical simulation results for EDI of Guediewaye, Thiaroye and Keur Massar. Finally, summary and conclusions are presented in Section 4.
2. Problem Formulation
The p-median model formulation is based on the following notations:
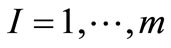 demand points.
demand points.
 facility locations for facilities.
facility locations for facilities.
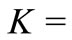 the maximum distance to be traveled by pupil.
the maximum distance to be traveled by pupil.
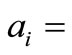 population (number of pupils) at the demand point
population (number of pupils) at the demand point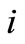 .
.
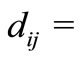 shortest distance between location
shortest distance between location 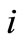 and location
and location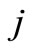 .
.
 number of school to be established.
number of school to be established.


The objective function minimizing the total weighted distance of assignment.
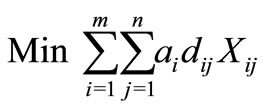 (1)
(1)
subject to
 (2)
(2)
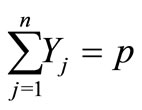 (3)
(3)
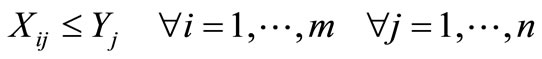 (4)
(4)
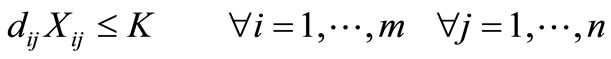 (5)
(5)
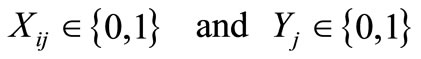 (6)
(6)
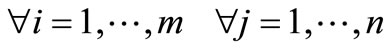
The objective function (1) minimizes the total weighted distance of assignment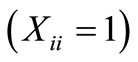 . When demand node i is assigned to a facility located at j, then
. When demand node i is assigned to a facility located at j, then 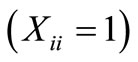 and the associated weighted distance
and the associated weighted distance 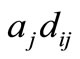 is included in the weighted distance sum. Constraint (2) ensures that each pupil must be assigned to at least one school. Constraint (3) restricts the placement or allocation of facilities to exactly p, where p is the number of high schools to be established. Constraint (4) maintains that any such assignment must be made to only those locations that have been selected for a facility. Constraint (5) imposes a maximum distance to be covered by each pupil. Constraint (6) represents the domain of variables.
is included in the weighted distance sum. Constraint (2) ensures that each pupil must be assigned to at least one school. Constraint (3) restricts the placement or allocation of facilities to exactly p, where p is the number of high schools to be established. Constraint (4) maintains that any such assignment must be made to only those locations that have been selected for a facility. Constraint (5) imposes a maximum distance to be covered by each pupil. Constraint (6) represents the domain of variables.
The model is solved using three EDIs in Dakar city: EDI of Guediawaye, EDI of Thiaroye and EDI of Keur Massar. We present in more detail only the results of Guediawaye’s EDI. The input data to solve this p-median problem are:
• a finite number of demand points with demand values to specify the location and amount of demand that needs to be satisfied.
• a finite number of facility locations. These are the only positions where facilities can be established. Several values of 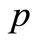 are tested for the three EDI.
are tested for the three EDI.
• distances between demand points and facility locations. Distances are calculated from the network of Dakar city.
• the population at demand point . The population represents the number of pupil at school
. The population represents the number of pupil at school .
.
3. Simulation Results
3.1. EDI of Guediawaye
Guediawaye is located on the coast of Dakar in the southeast of Pikine. It covers 550 square kilometers. In 2002, Guediawaye became the fourth department of the Dakar region, such as Dakar, Pikine and Rufisque. It is divided into five district municipalities: Golf Sud, Medina Gounass, Ndiarme Limamoulaye, Sahm Notaire and Wakhinane Nimzatt. There is in the EDI of Guediawaye ten secondary schools and two high schools. The large number of pupils requires significant renovation decisions or reconstruction of new locations. After exam, pupils are assigned to the nearest high schools. The question is which site to choose, which site is to expand, how many locations will be rebuilt and where to place such sites so as to minimize the distance traveled by pupils. The option is to compare the current situation (in number of pupils and schools) in simulations where the same number of pupils is assigned to different schools in reduced number and location.
• It begins with an analysis of the demand (here inelastic). Regularly registered pupils are listed on a map based on their domicile;
• Then we group the 15 demands points separated by less than 2 kilometers.
• Next we build a map of:
a) location of potential sites using the following criteria:
i) available land, in process, of being public or subject to expropriation.
ii) no nuisances by the school and for school. In total, this gives 8 points provides (including existing).
b) defined points of demand and supply; we can run a model and compare its results with those of the current situation.
Table 1 shows weights for the each demand; and Table 2 indicates distances between schools and sites.
Figure 1 is the map (Seye [10], Fagueye [11]) showing the 15 demands points in Guediawaye locality, where facilities are represented in red. The sites are: Joseph Correa A (JCA), Islamic Bank (BI), Ndiarka Diagne (NKD), Teachers’s City (CE), Site 1 (S1), Unit 5 (U5), Site 2 (S2), Site 3 (S3), Ogo Diop (OD), Joseph Correa B (JCB), Pikine East A (PEA), Pikine East B (PEB), Serigne Cheikh Anta Mbacke (SCAM), Pikine Secondary School (LPk), Limamoulaye Secondary School (LSS).
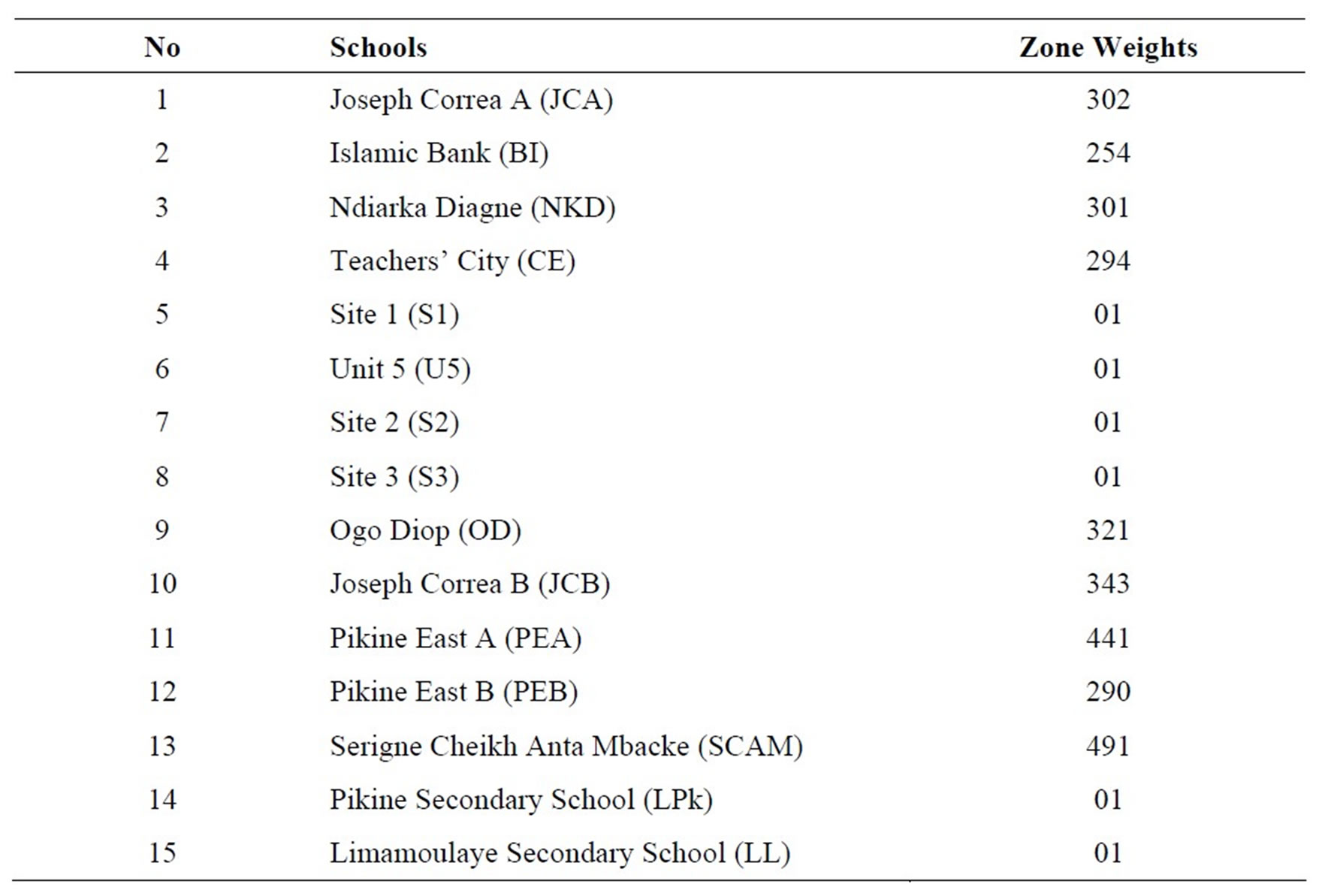
Table 1. Demand points and zone weights.
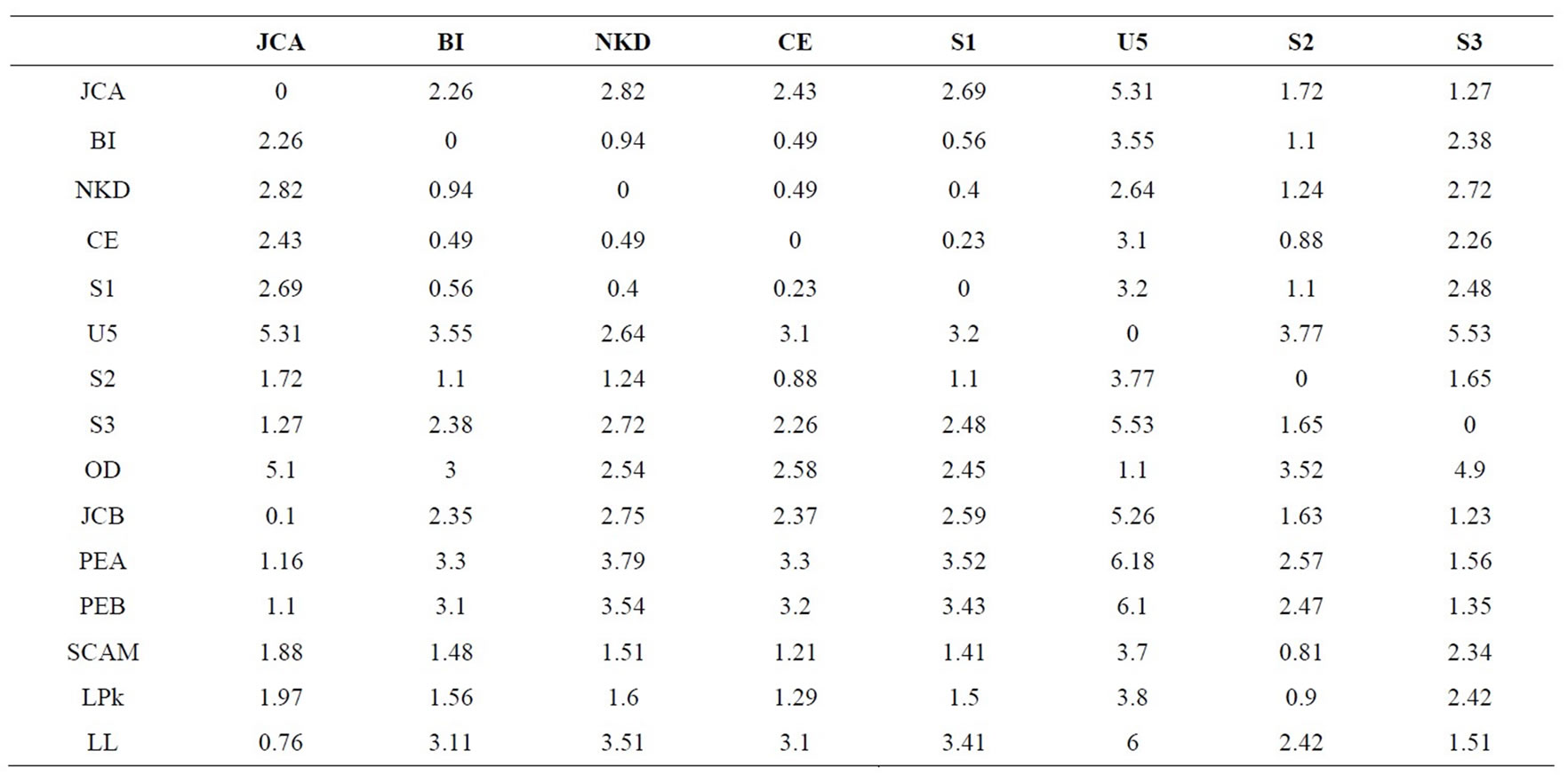
Table 2. Distances between schools and sites (in km).
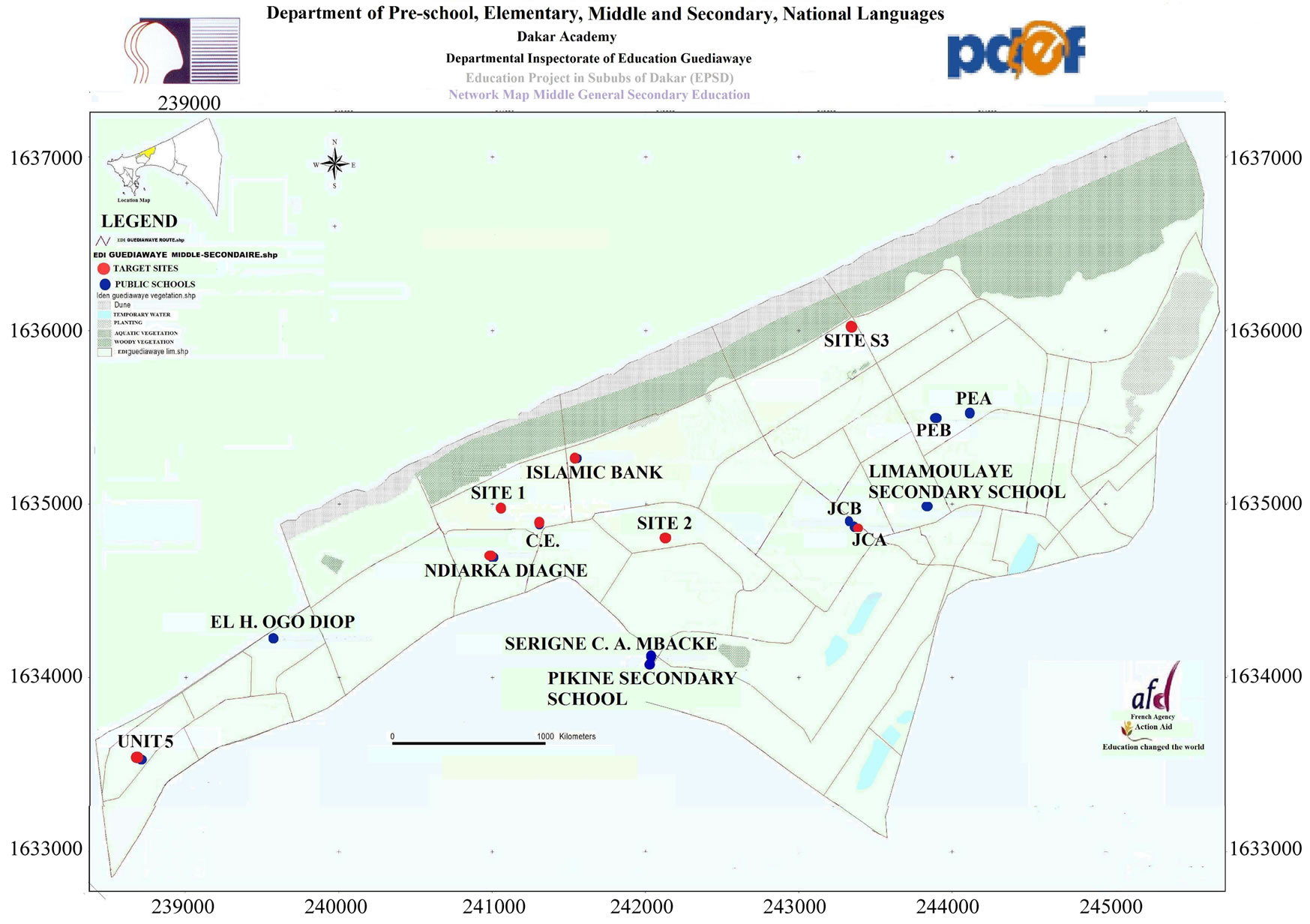
Figure 1. Sites for Guediawaye’s EDI.
Site 1, Site 2 and Site 3 are available land or in process or subject to expropriation, thus the population is put to 1. Pupils in Unit 5, LPk and LL do not live in these locations; they leave their home to come to these schools.
The 8 facility locations are: Joseph Correa A (JCA) (location 1), Islamic Bank (BI) (location 2), Ndiarka Diagne (NKD) (location 3), Teachers’s City (CE) (location 4), Site 1 (S1) (location 5), Unit 5 (U5) (location 6), Site 2 (S2) (location 7) and Site 3 (S3) (location 8).
The numerical tests were performed by using the commercial MILP solver, namely IBM-CPLEX V12.3 [9]. The numerical experiments were executed on a computer: 2×Intel(R) Core(TM) 2 Duo CPU 2.00 GHz, 4.0 GB of RAM, under UNIX system. We apply the p-median model for the targeted sites by setting 4 values for p. We have done tests for p = 5, 6, 7 and 8. We give here more details for the case p = 5. The procedure is the same for others (p = 6, 7 and 8).
Table 3 shows the facility locations for this scenario. Site 1, Site 2 and Site 3 are available land or in process or subject to expropriation, thus the population is put to 1. Pupils in Unit 5, LPk and LL do not live in these locations, they leave their home to come to these schools.
With the given 5 sites and from 8 facility locations, the
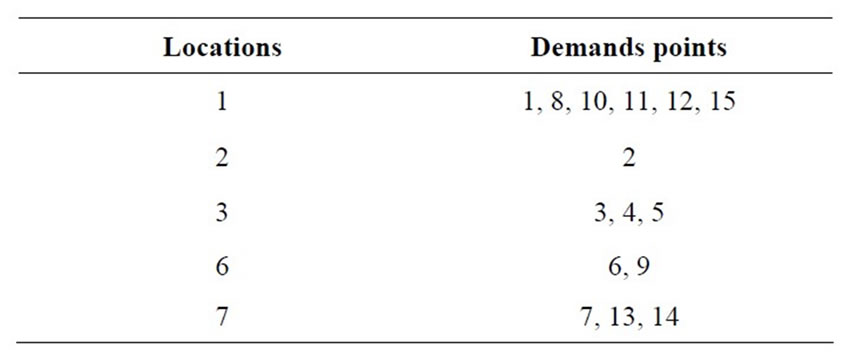
Table 3. Results for the EDI of Guediawaye.
optimal locations are Joseph Correa A (location 1), the Islamic Bank (location 2), Ndiarka Diagne (location 3), Unit 5 (location 6) and the Site S2 (location 7). The determination in choosing which pupils allocated at these facility locations depends on the distance between demand points and facility locations (see Table 3).
1) Pupils from Joseph Correa A, Joseph Correa B, Pikine East A, Pikine East B and nearby Site 3 will be assigned to the “High School Joseph Correa A”. And it is possible to assigned pupils from Limamoulaye if necessary.
2) Pupils from Islamic Bank are assigned to their new “High School Islamic Bank”.
3) Pupils from Ndiarka Diagne, Teachers’ City and nearby Site S1 will be assigned to the “High School Ndiarka Diagne”.
4) Pupils from Unit 5 and Ogo Diop are assigned to the new “High School Unit 5”.
5) Pupils from Serigne Cheikh Anta Mbacke and those living around 2 km of the Site 2 will be assigned to the “S2 High School”. And it is possible to assigned pupils from Pikine Secondary School if necessary.
It is determined by the value 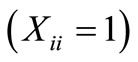 when we solved the p-Median problem. Figure 2 (Seye [10], Fagueye [11]) shows results; and the objective function value is 1619.490.
when we solved the p-Median problem. Figure 2 (Seye [10], Fagueye [11]) shows results; and the objective function value is 1619.490.
3.2. EDI of Thiaroye
Thiaroye is a district in Dakar, Senegal. It is located in the southern department of Pikine. There are twelve secondary schools in the EDI of Thiaroye, where six can become high schools and a site where a new high school can be built. With the given 4 sites and from 7 facility locations the optimal locations are Thiaroye Azur, Mbao Kambe, Thiaroye secondary school and Mbao secondary school. The numerical results for 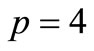 are shown in Figure 3.
are shown in Figure 3.
3.3. EDI of Keur Massar
Keur Massar is one of the sixteen boroughs in the city of Pikine. There are thirteen secondary schools in the EDI of Keur Massar when four can be enlarged in order to build high schools; and four sites where new high school can be built. With the given 5 locations and from 8 facility locations, the optimal locations are Malika, Keur Momar Marme Diop, Yembeul secondary school, Site 7 and Site 8. In this case, the maximum distance that allows us to obtain results using the IBM-CPLEX’s MILP solver is 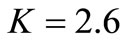 km; because with
km; because with 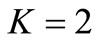 km, the model does not offer a solution. The numerical results for
km, the model does not offer a solution. The numerical results for 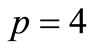 are shown in Figure 4.
are shown in Figure 4.
4. Conclusion
In this paper, we have presented school locations for pupils from secondary school to high school. An allocation model using the p-median problem is proposed. We have solved the related mixed-integer 0 - 1 linear program; and have shown how the simulation techniques can be applied successfully to practical decision support of the EDI of Dakar. All facility locations are connected
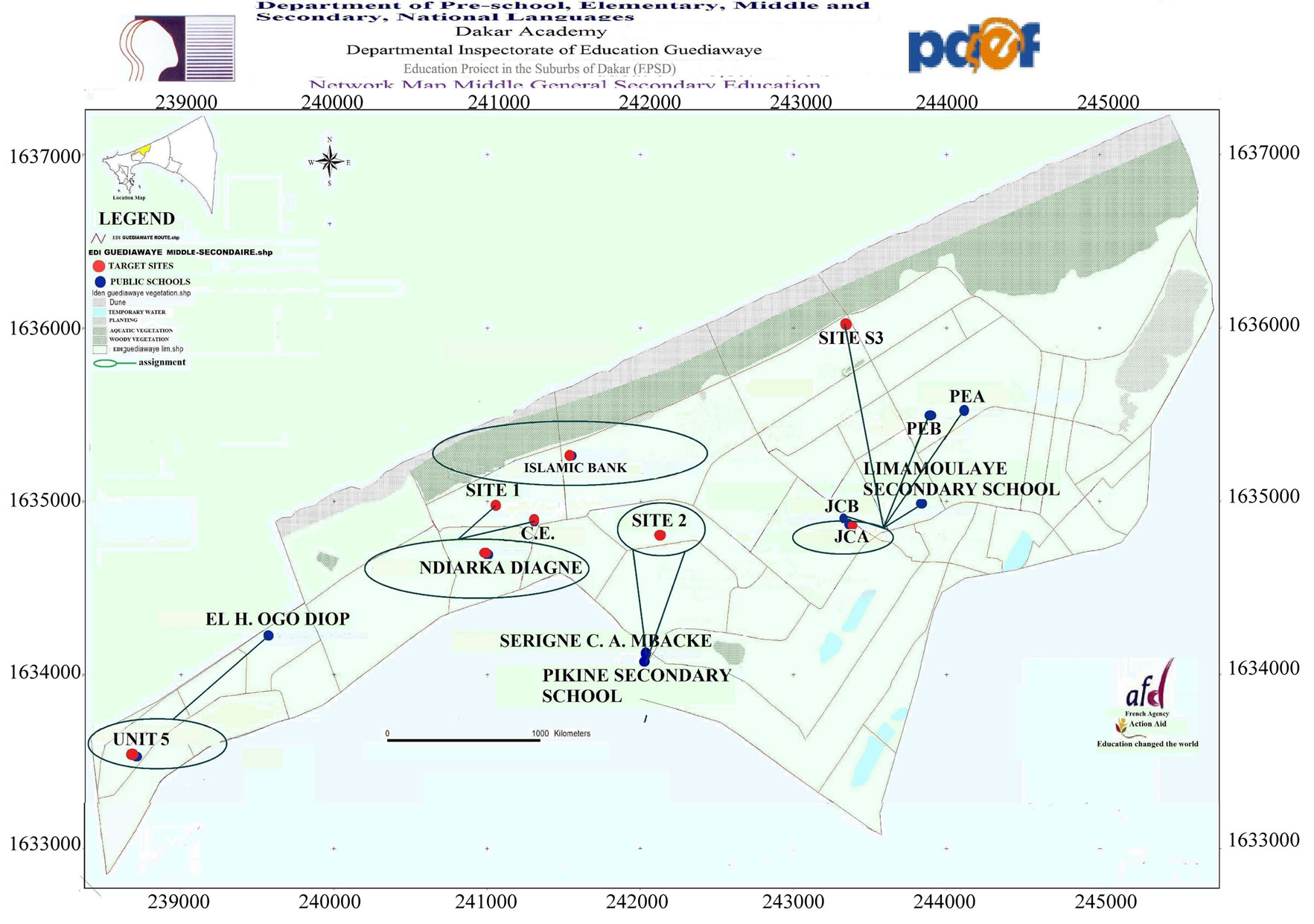
Figure 2. The facilities for Guediawaye’s EDI.
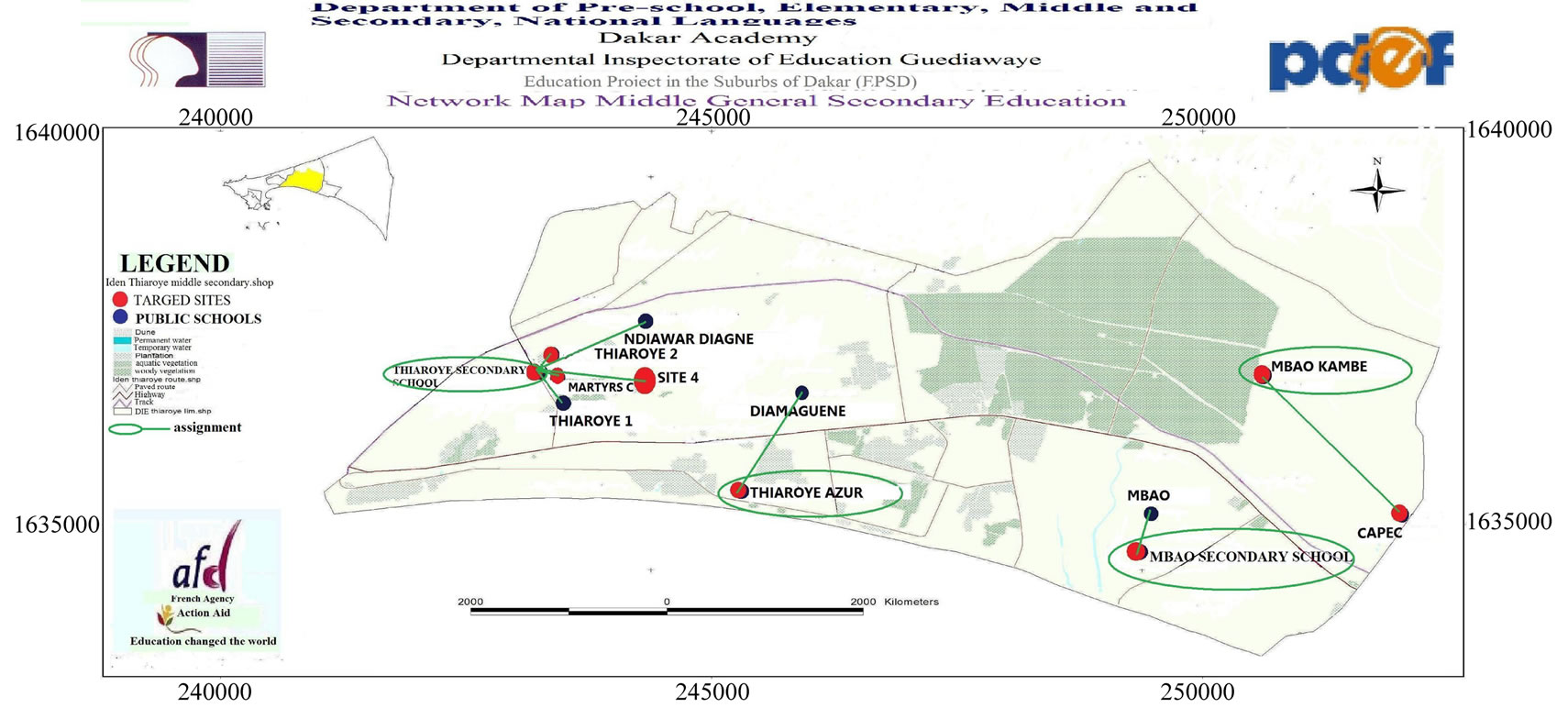
Figure 3. Sites for Thiaroye’s EDI.
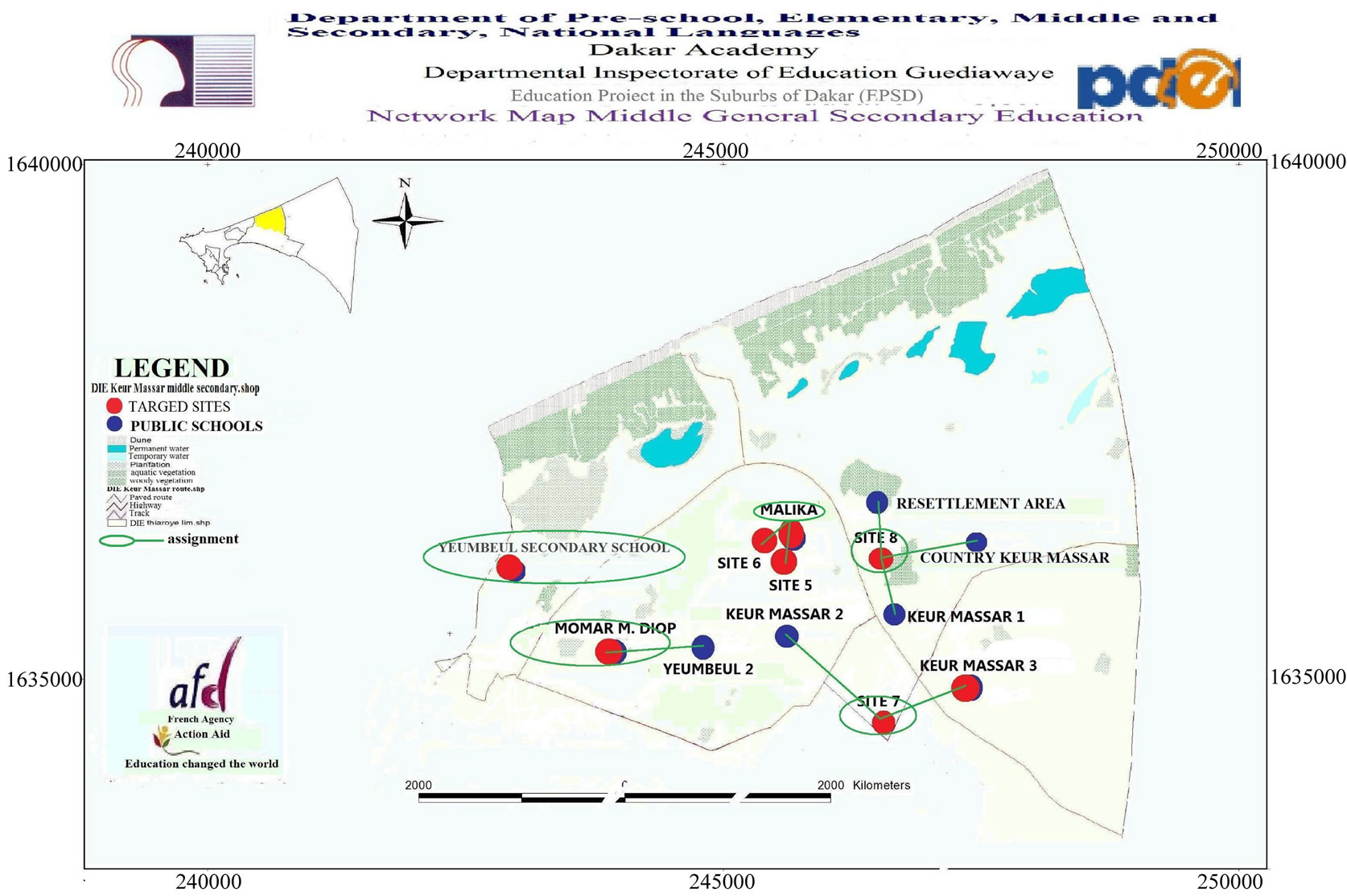
Figure 4. Sites for Keur Massar’s EDI.
to the demand points according to the shortest distances between them.
5. Acknowledgements
We thank EDI of Dakar specialists for the fruitful discussions. Also we would like to thank M. Amadou G. Seye for providing the data, and discussions related to the meaning of the data.
REFERENCES
- Z. Drezner, “Facility Location: A Survey of Applications and Methods,” Springer-Verlag, New York, 1995.
- M. R. Nooradelena and A. G. Noraida, “An Application of the p-Median Problem with Uncertainty in demand in Emergency Medical Services,” Proceedings of the 2nd IMT-GT Regional Conference on Mathematics, Statistics and Applications, Universiti Sains Malaysia, Penang, 13-15 June 2006.
- S. L. Hakimi, “Optimization Locations of Switching Centers and the Absolute Centers and Medians of a Graph,” Operations Research, Vol. 12, No. 3, 1964, pp. 450-459. doi:10.1287/opre.12.3.450
- R. Honey, G. Rushton, P. Lononis, B. Dalziel, M. Armstrong, S. De and P. Densham, “Stages in the Adoption of a Spatial Decision Support System for Reorganizing Service Delivery Regions,” Environment and Planning C, Vol. 9, No. 1, 1991, pp. 51-63. doi:10.1068/c090051
- D. Willer, “A Spatial Decision Support System for Bank Location: A Case Study,” NCGIA Technical Report, Vol. 90, No. 9, 1990.
- P. Chardaire and J. L. Lutton, “Using Simulated Annealing to Solve Concentrator Location Problems in Telecommunication Networks,” In: R. V. Vidal, Ed., Applied Simulated Annealing, Springer, Berlin, 1993, pp. 175-199. doi:10.1007/978-3-642-46787-5_9
- P. Densham and G. Rushton, “A More Efficient Heuristic for Solving Large p-Median Problems,” Papers in Regional Science, Vol. 71, 1996, pp. 307-329.
- R. L. Church and C. S. ReVelle, “The Maximal Covering Location Problem,” Papers in Regional Science, Vol. 32, No. 1, 1974, pp. 101-118. doi:10.1007/BF01942293
- IBM ILOG CPLEX Optimization Studio V12.3, Inc., “Using the CPLEXR Callable Library and CPLEX Barrier and Mixed Integer Solver Options,” 2011. http://www-01.ibm.com/software/integration/optimization/cplex-optimization-studio
- A. G. Seye, “School Map Office,” Department of National Education in Senegal, 2009.
- F. Ndiaye, “Surveys of District Mayors, Municipal Agents, Heads of Establishments Involved in EDI of Guediawaye,” 2010.

