Engineering, 2010, 2, 103-106
doi:10.4236/eng.2010.22014 Published Online February 2010 (http://www.scirp.org/journal/eng).
Analytic Computation Method of the Equivalent Thickness
of Superposition Multi-Throttle-Slices of Twin-Tubes
Shock Absorber
Changcheng Zhou, Yingzi Xu
School of Transport and Vehicle Engineering, Shandong University of Technology, Zibo, China
Received August 27, 2009; revised September 22, 2009; accepted October 4, 2009
Abstract
By elastic mechanics, the deformation of single throttle-slice for shock absorber was analyzed, the formula of
its deformation was established. According to the relation of the deformation of multi-throttle-slices with the
pressure on each slice, the analytic formula of equivalent thickness of multi-throttle-slices was established.
Followed is a practical example for the computation of the equivalent thickness of multi-throttle-slices, com-
pared the computed results with that simulated by ANSYS. The results show that the computation method of
equivalent thickness of multi-throttle-slices is accurate enough.
Keywords: Twin-Tubes Shock Absorber, Multi-Throttle-Slices, Equivalent Thickness, Analytic Computation
1. Introduction
With the improvement of automobile technology, the
velocity also improves, and there is a higher request to the
smoothness and the security [1,2]. The characteristic of
shock absorber influences driving smoothness and secu-
rity of vehicles, nevertheless, it depends on the quality of
the design and manufacture of shock absorber [3]. The
telescopic twin-tubes shock absorber is widely used for
vehicles. Nevertheless, it is still a puzzling problem for
the throttle valves parameters design to calculate accu-
rately the equivalent thickness of muti-throttle-slices. At
present, both in domestic and abroad, in despite of many
scholars analyzed the computation of equivalent thickness
of multi-throttle-slices mostly by the finite element
methods, they given out some qualitative conclusions
only. This situation is un-accommodated to highly devel-
oped technology of automobile and affects the design
quality of shock absorber. For the parameters design of
throttle valves, there is not any analytic method yet, only
with the experience of designer, testing and modification
repeatedly [4,5]. It is said that the design for parameters
of multi-throttle-slices, firstly a parameter value is guess-
timated on experience, then testing and modification time
and again; at lastly, the design value is fixed. While one
parameter changing, other parameters would also change.
Therefore, this method is inaccurate, the parameters of
multi-throttle-slices could not been designed reliably. The
traditional method of the equivalent-thickness of multi-th-
rottle-slices is only a numerical simulation value [6,7],
but it is unable to offer an analytic formula used to design
the parameters of multi-throttle-slices.
In this paper, the analytic computation method of
equivalent thickness of multi-throttle-slices was resear-
ched, the formula of equivalent thickness was established,
and the results computed were tested with software
ANSYS.
2. Deformation of Single Throttle-Slice
2.1. Mechanics Model of Single Throttle-Slice
Figure 1 is the mechanics model of elastic throttle slice.
The boundary conditions of throttle slice are fixation
restriction at the inner radius, and free restriction at the
outer radius.
Figure 1. Mechanics model of elastic throttle-slice.

C. C. ZHOU ET AL. 104
where, ra is the inner radius, rb is the outer radius, h is the
thickness, p is the pressure, and fr is the deformation at
radius r.
2.2. Math Model of Throttle-Slice Deformation
Being symmetrical about the z-axis, the load and the
structure, according to the basic principles in the elastic
mechanics, the differential equation of elastic throttle
slice deformation [8] is established as
2 2
22
dd d1d 1
()( )
ddd d
rr
ff
Dp
rrrrrr

2
(1)
where, 3
/[12(1 )]DEh


[,]
ab
rrr
; r is the any radius of
throttle slice, ; E is the elasticity coefficient of
material of throttle slice;

is Poisson rate; h is the
thickness of throttle slice. So, the solution of (1) is as
24
22
12 343
3(1 )
Cln Cln CC16
r
rp
frrrrEh
 
  (2)
where, C1, C2, C3, C4 could be defined by the boundary
conditions of throttle slice.
Therefore, analyzed the solution of the differential
equation of slice deformation, the each items of it has the
common factor of p/h3 that can be bringing forward from
(2), and then the deformation of throttle slice at any
radius r can be obtained.
4
22
C1C2C3 C43
3(1 )
[K lnKlnKK]
16
r
rp
frrrrEh
 
  (3)
where, KC1, KC2, KC3 and KC4 are the residual parameters
after the common factor p/h3 is binging forward respec-
tively from C1, C2, C3 and C4.
2.3. Formula of Throttle-Slice Deformation
Define Gr as the deformation coefficient of throttle slice,
it is as follow [9,10]
4
22
C1C 2C 3C 4
3(1 )
Kln Kln KK16 r
r
rrrr E
 
 G (4)
The Gr is the inherent characteristic of throttle-slice
deformation at radius r, denoting the deformation capa-
bility of throttle-slices.
So, the analytic formula of throttle-slice deformation
at any radius was written briefly as
3
rr
p
fG
h
 (5)
For example, one throttle slice’s Gr is shown as in
Figure 2.
3. Equivalent Thickness of Multi-Throttle-
Slices Superposition
3.1. Model of Multi-Slices Equivalent Thickness
The sketch of the equivalent thickness of multi-throttle-
Figure 2. Curve of throttle slice deformation coefficient vs.
radius.
h1
h2

hn
he
Figure 3. Sketch of multi-throttle-slices superposition.
slices superposition is shown in Figure 3.
3.2. Formula of Multi-Slices Equivalent
Thickness
The model of throttle-slices superposition with unequal
thickness could be taken as the paralleled springs that
have the equal length, unequal elasticity coefficient.
The deformations of multi-slices are equal under same
pressure. According to (5), it can be obtained such as
12
33 3
12
..... n
rrr r
ne
p pp p
GGG G
hh h

3
h
(6)
The forces on multi-slices are unequal, but the sum-
mation of theirs is equal to the total force, i.e.
12
... n ppp p

 .
Form (19), the equivalent thickness he is written as
33
3
12
...
e
hhh h
3
n

 (7)
If the each slice of multi-throttle-slices has multi-
group thickness, i.e. h1, n2; h2, n2; … hn, nn, so, (7) can be
expressed
33
3
112 2...
en
hnhnh nh
3
n
(8)
If the thickness of multi-throttle-slices is be equal each
other, i.e. h1=h2 …=hn, thus (7) can be written as
3
1e
hhn (9)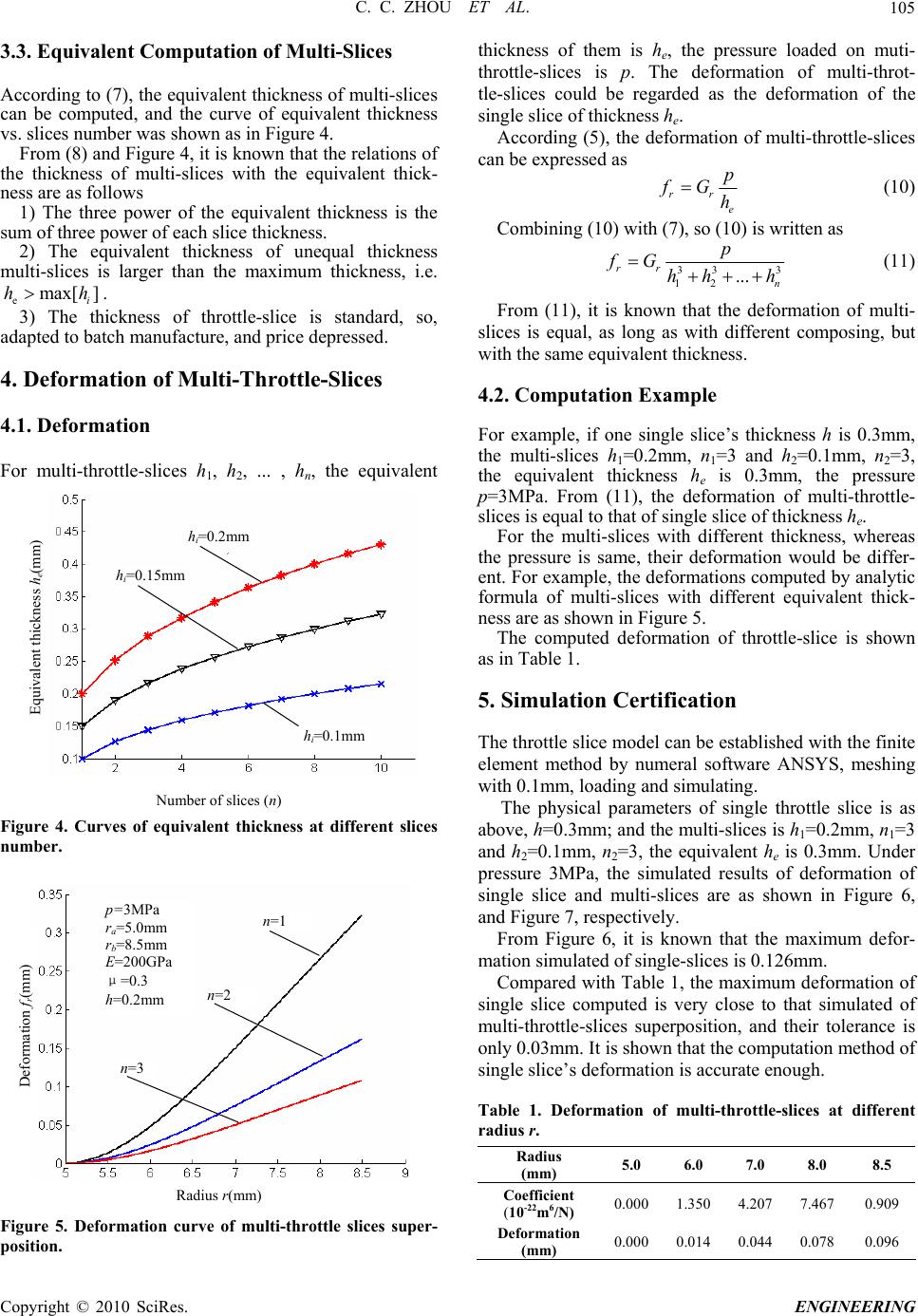

C. C. ZHOU ET AL.105
Radiu (mm)
Figure 5. Deformation rottle slices super-
position.
ices is p. The deformation of multi-throt-
3.3. Equivalent Computation of Multi-Slices
According to (7), the equivalent thickness of multi-slices
can be computed, and the curve of equivalent thickness
vs. slices number was shown as in Figure 4.
From (8) and Figure 4, it is known that the relations of
the thickness of multi-slices with the equivalent thick-
ness are as follows
1) The three power of the equivalent thickness is the
sum of three power of each slice thickness.
2) The equivalent thickness of unequal thickness
multi-slices is larger than the maximum thickness, i.e.
.
emax[ ] i
hh
3) The thickness of throttle-slice is standard, so,
adapted to batch manufacture, and price depressed.
4. Deformation of Multi-Throttle-Slices
4.1. Deformation
F
or multi-throttle-slices h1, h2, ... , hn, the equivalent
Number of slices (n)
Figure 4. Curves of equivalent thickness at different slices
number.
s r
curve of multi-th
thickness of them is he, the pressure loaded on muti-
throttle-sl
tle-slices could be regarded as the deformation of the
single slice of thickness he.
According (5), the deformation of multi-throttle-slices
can be expressed as
rr
p
fG
h
 (10)
e
Combining (10) with (7), so (10) is written as
333
12
...
rr
n
hh h
p
fG 

 (11)
From (11), it is known that the defor
slices is equal, as long as with different composing, but
wi
’s thickness h is 0.3mm,
3 and h2=0.1mm, n2=3,
blished with the finite
are ANSYS, meshing
1 1
mation of multi-
th the same equivalent thickness.
4.2. Computation Example
For example, if one single slice
the multi-slices h1=0.2mm, n1=
the equivalent thickness he is 0.3mm, the pressure
p=3MPa. From (11), the deformation of multi-throttle-
slices is equal to that of single slice of thickness he.
For the multi-slices with different thickness, whereas
the pressure is same, their deformation would be differ-
en
Equivalent thickness he(mm)
hi=0.2mm
hi=0.15m
m
t. For example, the deformations computed by analytic
formula of multi-slices with different equivalent thick-
ness are as shown in Figure 5.
The computed deformation of throttle-slice is shown
as in Table 1.
hi=0.1mm
5. Simulation Certification
The throttle slice model can be esta
element method by numeral softw
with 0.1mm, loading and simulating.
The physical parameters of single throttle slice is as
above, h=0.3mm; and the multi-slices is h=0.2mm, n=3
and h2=0.1mm, n2=3, the equivalent he is 0.3mm. Under
pressure 3MPa, the simulated results of deformation of
single slice and multi-slices are as shown in Figure 6,
and Figure 7, respectively.
From Figure 6, it is known that the maximum defor-
mation simulated of single-slices is 0.126mm.
p=3MPa n=1
ra=5.0mm
Compared with Table 1, the maximum deformation of
single slice computed is very close to that simulated of
multi-throttle-slices superposition, and their tolerance is
only 0.03mm. It is shown that the computation method of
single slice’s deformation is accurate enough.
Table 1. Deformation of multi-throttle-slices at different
adius r. r
Radius
(mm) 5.0 6.0 7.0 8.0 8.5
Coefficien
0-22m6/N
t
(1) 0.000 1.350 4.207 7.4670.909
Def
(mm) 0.000 0.014 0.044 0.0780.096
ormation
rb=8.5mm
E=200GPa
μ=0.3
h=0.2mm
Deformation fr(mm)
n=2
n=3

C. C. ZHOU ET AL. 106
Figure 6. Deformation map simulated of single-throttle
slices.
Figure 7. Deformation map simulated of multi-throttle-slices
superposed.
nalytic computation and simulation certificatio
ickness of multi-throttle-slices, it is
lytic formula of equivalent thickness
With it, the equivalent thickness of multi-throttle-slices
with different thickness can computed accurately.
The deformation comput of multi-slices is close to
e-
sli
re Science Foundation of
) for the funding support.
] D. F. Yu and Q. H. Chen, “Design study of smooth-
nsion shock absorber outer
characteristic,” Acta Armamentarll: The Volume of Tank,
for small electric vehicles,” Journal of Asian Elec-
ce and
c Vehicles,
ian Electric Vehicles,
. 10–16, 2001.
. 19–21,
u, L. Gu, and L. Wang, “Bending deformation and
l. 26, No. 7, pp. 581–584, 2006.
. 43, No.
be
ed
that simulated by ANSYS. It is shown that the computa-
tion method of the equivalent thickness of multi-throttl
ces is accurate enough, can be used to design the pa-
rameters of throttle-slices of shock absorber.
7. Acknowledgment
The authors thank the Natu
Shandong (No. Y2007F72
8. References
[1
ness-to-safety ratio in suspe
Armored Vehicle and Engine, Vol. 87, No. 3, pp. 11–17,
2002.
[2] C. C. Zhou, Z. Y. Zheng, and X. Y. Zhang, “Design
method for throttle holes area of telescopic shock ab-
sorber
tric Vehicles, Vol. 7, No. 1, pp. 1191–1197, 2009.
[3] X. M. Fen and Z. M. Liu, “Development and current
situation of automobile hydraulic telescopic damper
technology,” Journal of Wuhan University of Scien
Technology, Vol. No. 8, pp. 340–343, 2003.
[4] T. Ashida, D. Tanaka and S. Minami, “A method to de-
termine the velocity profiles from the power consumption
of electric vehicles,” Journal of Asian Electri
Vol. 5, No. 2, pp. 1027–1032, 2007.
[5] S. Matsugaura, H. Nishimura, M. Omae, et al, “Devel-
opment of a driver-monitoring vehicle based on an ultra
small electric vehicle,” Journal of As
Vol. 3, No. 2, pp. 758–762, 2005.
[6] S. M. Li, Z. H. Lü, “Technology development of cylindri-
cal fluid drag shock absorber for motor vehicle,” Automo-
bile Technology, Vol. 32, No. 8, pp
From Figure 7, it is known that the maximum defor
mation simulated of multi-throttle-slices is 0.101mm
-
respectively.
Compared with Table 1, the maximum deformation
computed of multi-throttle-slices superposition is close
to that simulated, the tolerance is only 0.005mm. It is
sh
[7] Y. Chen, H. E. Hui and J. F. Bai, “Analysis of hydraulic
shock absorber spring valve chip deformation of charade
car,” Automobile Technology, Vol. 31, No. 1, pp
2000.
[8] Z. L. Xu, “Elasticity mechanics,” Beijing: Higher Educa-
tion Press, 2001.
[9] C. C. Zho
own that the computation method of the equivalent
thickness of multi-throttle slices superposition is accurate
enough.
6. Conclusions
y the a
coefficient of throttle-slice,” Transactions of Beijing Institute
of Technology, Vo
Bn
[1
to the equivalent th
nown that the anak
6, pp
0] C. C. Zhou and L. Gu, “Superposition throttle slices
opening size and characteristic test of telescopic damper,”
Chinese Journal of Mechanical Engineering, Vol
. 210–215, 2007.
of multi-throttle slices is accurate, simple and applied.