Wireless Sensor Network, 2010, 2, 186-196
doi:10.4236/wsn.2010.22024 y 2010 (http://www.SciRP.org/journal/wsn/). Published Online Februar
Achieving Directionality and Transmit Diversity via
Integrating Beam Pattern Scanning (BPS)
Antenna Arrays and OFDM
Peh Keong Teh, Seyed Alireza Zekavat
Department of Electrical and Computer Engineering, Michigan Technological University, Houghton, USA
Received July 28, 2009; revised October 25, 2009; accepted November 19, 2009
Abstract
In this paper, we introduce a novel merger of antenna arrays with scanning beam patterns, and Orthogonal
Frequency Division Multiplexing (OFDM) systems. Controlled time varying phase shifts are applied to the
antenna array elements mounted at the base station with beam patterns directed toward the desired user. This
creates a small beam pattern movement called Beam Pattern Scanning (BPS). In rich scattering environments
BPS creates a time varying environment leading to time diversity exploitable at the receiver enhances its
probability-of-error performance. Here, we apply OFDM signals to BPS antenna arrays, and we achieve: (1)
directionality, which supports Space Division Multiple Access (SDMA); and (2) a time diversity gain, which
leads to high performance. We discuss the structure of the base station antenna array and the OFDM receiver
that exploits time diversity. We also introduce the merger of BPS and multi-carrier OFDM (MC-OFDM)
systems. In MC-OFDM each bit is transmitted over all sub-carriers after serial to parallel conversion. BPS/
MC-OFDM receiver exploits both time diversity inherent in BPS, and frequency diversity inherent in
MC-OFDM transmission technique. Simulation results show high Probability-of-error performance is achie-
vable via BPS/OFDM and BPS/MC-OFDM schemes comparing to the traditional OFDM and MC-OFDM,
respectively. Simulations also reveal that MC-OFDM system as well as its merger with BPS is capable of
mitigating large Peak-to-Average Ratio (PAPR) problem in traditional OFDM system. In addition, perform-
ance simulations with coded OFDM (COFDM) and coded MC-OFDM (MC-COFDM) and their merger with
BPS are studied.
Keywords: OFDM, MC-OFDM, Antenna Array, Beam Pattern Scanning, Transmit Diversity.
1. Introduction
OFDM (Orthogonal Frequency Division Multiplexing) is
an emerging technique capable of high data rate trans-
mission over frequency selective channels without im-
plementation of complex equalizers [1–5]. Due to its
inherent benefits, OFDM has been proposed as the basic
modulation technique for the 4th generation wireless
systems. In an N sub-carriers OFDM system, a block of
N information bits are serial to parallel converted and
modulated via N orthogonal sub-carriers (each bit over
one sub-carrier). They are then summed and transmitted
simultaneously [1–5]. This process extends the symbol
duration from Ts to NTs.
MC-OFDM (Multi-Carrier OFDM) is an innovative
OFDM transmission technique where each MC-OFDM
user’s bit is transmitted over all available sub-carriers
simultaneously [6–8]. To ensure separability of the bits
at the receiver and reduce inter-bit-interference (IBI),
orthogonal codes, e.g., Hadamard Walsh codes, are ap-
plied to the sub-carriers of each bit. Through MC-OFDM,
frequency diversity can be exploited to improve the per-
formance of the system with minimal complexity in the
transmitter and receiver [7,8].
Properly designed OFDM and MC-OFDM systems
convert the channel to a flat fading channel and eliminate
the need for complex equalizers. This is achieved via sel-
ecting N such that NTs becomes much larger than chan-
nel delay spread. However, there is a drawback associ-
ated with flat fading: If sub-carriers experience deep fade,
the bit will be rendered unrecoverable and thereby de-
grades the system probability-of-error performance. This
issue can be resolved via diversity techniques. In MC-
OFDM signals are transmitted over all sub-carriers,

P. K. TEH ET AL.187
which allow frequency diversity to be exploited at the
receiver [6–8]. Besides frequency diversity, various me-
thods such as: 1) Forward Error Correction Coding at the
cost of the overall system throughput [1,2], and 2) trans-
mit diversity has been used to improve the probability-
of-error performance of OFDM and MC-OFDM systems
[9,10]. In this work, we merge OFDM systems with a
transmit diversity scheme created via beam pattern
movement (scanning).
The concept of beam pattern movement has been ref-
erenced in the literature, some with a different approach,
and some with no further exploration. For example, in
[11], researchers introduce “jitter diversity”. In that work,
with a high angular spread at the mobile receiver, the
beam pattern is jittered around its usual position to create
angle diversity and enhance the receiver performance;
and it does not lead to time diversity. In [12], there is a
very short (just one line) reference to the idea of antenna
pattern movement to create time diversity. The authors
state that one can force the antenna to oscillate when the
vehicle is traveling at low speeds, channel’s fade is slow,
and time diversity cannot be exploited.
Recently, a powerful transmit diversity technique has
been introduced called beam pattern scanning (BPS)
(also known as beam pattern oscillation). In this scheme,
antenna arrays are installed at the base station (BS) with
their scanning (oscillating) antenna patterns directed to-
ward the desired users [13,15]. A time varying phase
shift is applied to each antenna element in order to steer
and move the antenna pattern within one symbol dura-
tion Ts (or within NTs in OFDM systems). The beam pat-
tern starts sweeping an area of space at time zero, it re-
turns to its initial position after time Ts (NTs in OFDM)
and repeats its sweeping. The movement of the beam
pattern is small, e.g., in the order of 5% of half power
beam width (HPBW). Hence, the desired user stays in
the antenna array HPBW at all times.
In rich scattering environments, as a result of the de-
parture and arrival of scatterers within the window of
antenna beam pattern, BPS creates a time varying chan-
nel with a small controlled coherence time Tc with re-
spect to Ts (NTs) [8,13,14]. This leads to a fast fading
channel via which time diversity benefits can be ex-
ploited at the receiver [16]. Therefore, BPS is introduced
as a transmit diversity scheme that enhances: a) receiver
probability-of-error performance via time diversity, and
b) wireless network capacity via Spatial Division Multi-
ple Access (SDMA) [17] or spatial filtering interference
reduction (SFIR) [18].
In this paper, we merge BPS transmit diversity with
OFDM and MC-OFDM systems. This merger achieves:
1) high probability-of-error performance by time diver-
sity induced at the receiver via BPS [8,15,19], and 2)
high capacity via directionality created via antenna ar-
rays mounted at the transmitter [17–20], with a 3) low
complexity due to the structure of OFDM and BPS. The
structure of BPS is simple because the complexity is
mainly focused at the base station antenna array.
In this work, we present and discuss: a) the antenna ar-
ray structure that makes BPS possible for OFDM systems
incorporating a number of sub-carriers, b) the OFDM
receiver structure capable of exploiting the time diversity
induced by BPS, and c) the MC-OFDM receiver capable
of exploiting time diversity via BPS and frequency diver-
sity through Multi-carrier scheme. We simulate the prob-
ability-of-error performance and the peak-to-average ratio
(PAPR) curves for both BPS/OFDM and BPS/MC-
OFDM.
Traditional OFDM and MC-OFDM utilizing antenna
arrays without BPS scheme are used as benchmark agai-
nst BPS/OFDM and BPS/MC-OFDM schemes. Adaptive
antenna arrays with beam patterns directed towards in-
tended users leads to capacity enhancement via SDMA
[20–22] without enhancing the performance. This paper
highlights performance benefits achieved through BPS
and OFDM systems (OFDM and MC-OFDM) merger. In
addition, coded version of OFDM systems and BPS
merged systems (BPS/COFDM and BPS/MC-COFDM)
are simulated and compared to further underline the per-
formance improvement through BPS merger.
Section 2 introduces OFDM and MC-OFDM systems,
BPS technique and the antenna array structure. In Sec-
tion 3, we present BPS/OFDM and BPS/MC-OFDM
received signal and their receiver structure. In Section 4,
we present the probability-of-error performance and
peak-to-average ratio simulations. Section 5 concludes
the paper.
2. OFDM, MC-OFDM, Antenna Array
Structure and BPS Techniques
1) OFDM system: In OFDM, a block of N bits are trans-
mitted simultaneously over N sub-carriers (each bit over
one sub-carrier) after serial to parallel conversion, which
converts the duration of transmitted symbols from Ts to
NTs (see Figure 1). The number of sub-carriers N is cho-
sen to ensure flat fading channel at all times (i.e., channel
delay spread Tm << NTs), and the sub-carriers are sepa-
rated by
s
NT
f1  (1)
to ensure the orthogonality of sub-carriers and avoid in-
ter-carrier interference at the receiver. The OFDM
transmitted signal corresponds to:
)(][Re)(
1
0
)(2
sNT
N
n
tfnfj
iiNTtgeiNnbts s
o





 




(2)
where b[·]{+1,-1} is the transmitted bit, i {0,1,2,…}
is the ith group of N bits simultaneously converted to par-

P. K. TEH ET AL. 188
NTs
allel (n represents the bit number), fo is the carrier fre-
quency and is a rectangular waveform of unity
height over zero to NTs (Ts refers to symbol duration).
)(tg s
NT
2) The MC-OFDM system: In MC-OFDM system, all
N bits are transmitted simultaneously over all N sub-
carriers. To maintain orthogonality across bits, an or-
thogonal code, e.g., Hadamard Walsh code, is assignedto
the sub-carrier of each bit (see Figure 2). By transmitting
all N bits simultaneously, the symbol duration is con-
verted from Ts to NTs. Hence, the MC-OFDM transmitted
signal corresponds to:
)(][Re)(
1
0
1
0
)(2
sNT
N
k
N
n
tfnfj n
ki iNTtgeiNkbts s
o









 




 

(3)
where is the kth bit and n
th sub-carrier orthogonal
codes’ element. Other parameters have been defined in
(2).
n
k

3) Proposed Antenna Array Structure: We assume an
M-element linear antenna array mounted at the Base Sta-
tion (B.S.) (Figure 3). In order to move the antenna pat-
tern, a time varying phase, m  (t), is applied to the mth
antenna array element (Figure 3). Moreover, in Figure 3
the angle 
o represents the direction of the antenna beam
pattern (angle-of-arrival of the signal) with respect to the
antenna array main axis. Here, for simplicity in presenta-
tion, it is assumed that the desired mobile is located at
angle

o = 0 (i.e., antenna array main axis and beam pat-
tern main axis are overlapped). In this case, the normal-
ized array factor characterizing the resulting antenna
pattern corresponds to:










),(sin
),(sin
1
),(
2
1
2



t
t
M
tAF
M
, (4)
where
)(sin
2
),(tdt
o



  . (5)
1
N
k

1
k

0
k

Nj
e

)1(2 
f
j
e)1(2

f
j
e)0(2

][kb
…
(b)
Figure 2. (a) MC-OFDM transmitter structure; (b) kth bit transmitter design.
(a)
)(tsi
Bit
1
tran
s
-
Bit
2
tran
s
-
Bit
K
tran
s
-
][kb
]2[b
…
]1[b
Information
bits
Figure 1. OFDM transmitter structure.
Serial to Parallel
]1[

Nb
]0[b
]1[b
ftj
e02

ftNj
e)1(2

tfj o
e
 2
Informa-
tion bits
b[0]
si(t)
. . .
b[N-1]
ftj
e12

NTs
C
opyright © 2010 SciRes. WSN

P. K. TEH ET AL.189
Here,

o is the wavelength (c/fo), d is the distance be-
tween antenna elements, and (2
 d/ 
o) sin
 represents
the phase offset due to the difference in distance between
antenna array elements and the mobile.
In general, antenna array half power beam width
(HPBW) changes with frequency (sub-carrier). For nar-
rowband OFDM systems, the variation in HPBW is neg-
ligible (see Figure 4); however, for wideband and high
data rate OFDM systems, e.g., 60 Mb/s data rate, the
variation of beam pattern with sub-carriers is consider-
able (see Figure 4). In order to achieve directionality via
sectoring strategy (e.g., in switched beam smart antenna
systems), identical beam patterns are required for all N
sub-carriers. Since different sub-carriers create different
HPBWs, users located near the border of two sectors
may experience either: 1) large interference from the
beam pattern of unintended sector, or 2) a reduction in
power in the desired signal in the beam pattern from the
desired sector [15].
We must then ensure that the size of sub-carriers ap-
plied to antenna array is small enough that all the
sub-carriers placed in the antenna array generate identi-
cal patterns. Hence, we introduce the following defini-
tion:
Definition 1: Beam Patterns are considered identical if
the variation in null-to-null beam width (B.W. in Figure
4) of the beam patterns created via sub-carriers are
within 10% of the average null-to-null beam width
(B.W.)ave. Based on this definition, it can be shown via
simulations that whenever the minimum frequency, fmin,
and the maximum frequency, fmax, applied to an antenna
array satisfy
01.0
.min.max 

o
f
ff , (6)
“identical” beam patterns are observed (see [15]). Con-
sidering a contiguous bandwidth for OFDM systems, this
criterion corresponds to
01.0


o
f
f
N (7)
If (6) is not satisfied, the N sub-carriers of the OFDM
system should be divided into P groups of Q ≤ N (N = PQ)
neighboring sub-carriers such that Q
 fo/f ≤ 0.01. Then,
either each set of Q sub-carriers should be applied into a
(a) (b)
Figure 4. 32 sub-carriers OFDM system, center frequency 4.0GHz. (a) Narrow band system with band-
width of 200MHz; (b) Wide band system with bandwidth of 2GHz.
Figure 3. Antenna structure.
OFDM or MC-OFDM
transmitter (Figures 1 & 2)
Information
bits
])([02 o tj  
])([12 o tj
e
e
 
])()[1(2 o tMj
e
 
Beam Pattern
Element #0
1Element #
Element #M-1
d
o

Main axis Di-
rection
Antenna Array
Main axis Di-
rection
y
x

P. K. TEH ET AL. 190
unique M-element antenna array or unique complex
should be applied to antenna elements for each set weights
of sub-carriers [15,17,19]. In this work, we assume a nar-
row band system with Q = N, P = 1, i.e., all of sub-carri-
ers, fn = fo + n  f, n  {0,1,…,N-1} are applied to one an-
tenna array (see Figure 3).
4) Beam Pattern Scanning Technique: The scanning of
beam pattern is created at the B.S. by applying time
varying phase offsets m  (t) to the antenna array element
m{1,2, …,M} (Figure 3). The antenna array’s beam
pattern movement should ensure: 1) constant large scale
fading, and 2) L independent fades to be generated within
each NTs. This creates an L-fold diversity gain at the mo-
bile receiver. After each NTs,
 (t) returns the beam pat-
tern to its t = 0 position and repeats an identical spatial
sweeping movement over the next NTs period (Figure
5(a)).
In order to ensure constant large-scale fading, the mo-
bile must remain within the antenna array’s HPBW over
each symbol duration NTs. This condition corresponds to
[22].
10,  

dB
dt
NTs
where B is the HPBW,  is the azimuth
(8)
angle (direction
of arrival), d
 /dt is the rate of antenna pattern movement,
and NTs·(d
 /dt) is the amount of antenna pattern move-
ment within NTs. The parameter  , 0 <  < 1, is the con-
trol parameter ensures the received antenna pattern am-
plitude is within the HPBW for the entire symbol dura-
tion. The phase offset applied to the antenna array is
calculated using (8) leads to [9] (see Figure 5(b)):





 cos2 )( s
NT
t
Bd
t


 2
so NT

(9)
Specifically, to solve for (9) from (8) (detail
we p
of scat-
ed in [20]),
roceed as follows: 1) Using (5), we solve for  at a
fixed value of
 (t,  ) = 
o; 2) substituting this
 value into
(8) and differentiating, we create a differential equation
for
 (t); and (3) finally, we solve the differential equation
which leads directly to (9).
Sweeping of the antenna pattern creates a time-varying
channel with a coherence time that is a function
tering environment and may lead to L independent fades
over NT s. Geometric-based stochastic channel modeling
scheme is used to evaluate the channel diversity gain
[11]. Channel coherence time calculated in [15] assum-
ing a medium size city center (e.g., 3 scatterers per
1000m2), with 0.0005 <  < 0.05 shows that diversity
gain as high as L

7 is achievable via BPS scheme. The
main assumption in this modeling scheme is:
1) A semi-elliptical coverage with the mobile at its
center (suitable when we assume the height of the BS
er Design
plicity in presentation, we con-
i = 0
(10)
Applying this signal to the antenna array in
the outh
(11
The total normalized downlink
sid
0
MS
BS
antenna array is close to the height of surrounding build-
ings);
2) The movement generated by antenna array oscilla-
tion is dominant, and hence the movement of mobile and
other relative speed object in the environment is ignored;
3) Scatters are assumed to have dimensions in accor-
dance with a known PDF [13];
4) Scatters in the surrounding BS are uniformly dis-
tributed;
5) Scatters are consider diffused reflectors which re-
flect the incident radiation in all direction; and,
6) The signal received at the mobile is sum of hori-
zontally propagated plane waves interacting with just one
scatterer.
3. Receiv
1) BPS/OFDM: For sim
sider in (2). We represent the OFDM transmitted
signal as:
)(
1
0
N
ts 

 ],0[,)(2cos][
0
s
n
oNTttfnfnb 


Figure 3
tput of the m element of the antenna array is
  ,0[,)()(cos][)(
1N
NTttmtfnfnbts  

 ]2
0
s
n
om

)
transmitted signal, con-
ll m) is: ering all antenna elements (a

(t)
NTs
o
d




cos2
S
NT
t
Figure 5. (a) Beam pattern scanning; (b) Antenna element delay line function.
(b)
(a)
C
opyright © 2010 SciRes. WSN

P. K. TEH ET AL. 191
 ],0[)()(2cos
1
][)(
1
0
1
0
s
M
m
o
N
n
NTttmtfnf
M
nbts   




(12)
Since the range of the control parameter ien 0 <

< 0.05 in the frequency offset induced by
 (t) in the
transmitted signal is less than 5% and can be ignd.
Typically, as it is seen in (9), assuming half wavelength
spacing across antenna elements, a = 128, and B  
/ 6 (for 4 element antenna), and T = 10-6, the maximum
frequency drift would be in
minimal compared to the typical carrier frequency of 2.4
GHz. At the receiver side, considering the transmit diver-
sity leads to L-fold time diversity, the received signal
[0,NTs] can be divided into time slot
l
s tak
(8),
ore
nd N
s
the order of 100 Hz, which is
s [lNTs/L, (l+1)NTs/L],
{0,1,…,L-1}, and these time slots demonstrate inde-
pendent fades. The received signal can then be repre-
sented as

 




1
0
1
0
)(2cos
1
][
1
)(
M
m
o
N
n
n
ll tfnf
M
nb
L
tr 

]/)1(,/[)(),( LNTlLlNTttntmssl
n
l

(13)
where, nl(t) is an additive white Gaussian noise (AWGN),
which is independent for different time slots (l), n
l
 is
the Rayleigh fade amplitude on nth sub-carrier in the lth
time slots, and n
l
 is the fading phase offset in the nth
sub-carrier th and me slot (hereafter, this pha
is assumed to be tacked and removed). The Raylei
amplitudes are dered independent over tim
related over suers. The correlation coeffici
tween carrier is characterized by [23]
l ti
r
consi
b-carri
' and
se offset
gh fade
ent be-
e and cor-
n''n

2
'',' ))/(()'''(1
1
c
nn ffnn
p  (14)
where (∆f) is the coherence bandwidth of the channel.
Moreover,
c
),(


t in (13) is introduced in (5). Applying
the summation over m, (13) corresponds to
cos),(][)(
1
0
 


 tAFnbtr
N
n
n
ll
)(),(
2
1
)(2 t
M
tfnfo


  tnn
l


 (15)
Here, AF(t,  ) introduced in (4), is the n
tenna array factor. Assuming a narrow-be
ak d
na array pat-
tern over NTs, the array factor experience over [0,NTs] is
well approximated by AF(t,  )  1.
The BPS/OFDM receiver is shown in Figure 6. In this
figure, “Re” refers to Real Part, and “Im” refer
Imaginary Part. In addition, after the application
ormalized an-
am width an-
tenna array and the mobile is located at 
o = 0, (5) can be
approximated by
 (t,  ) =  (t) =  (t). Assuming that an-
tenna array peirected towards the intended mobile at
time 0, and with small movements of anten
s to
of







)(
2
1
2
2
1t
M
tfj
s
o
e
NT
v

(16)
and returning the OFDM to baseband, a bank of band-
pass filters are used to separate the OFDM signal into its
N multiple sub-carriers: The baseband signal is inte-
grated over each interval of t  [lNTs/L, (l+1)NTs/L], l 
{0,1,…,L-1} in order to exploit time diversity components
cr
Figure 6. BPS-OFDM receiver.
eated by beam pattern scanning [14,15]. The received
signal for each subcarrier, n and l time slot corresponds to
)(trlRe{·}
to
Im{
·
}
v
Band Pass
Filter
Band Pass
Filter
ftj  02 
e0
l
r
Band Pass
Filter
ftj
e 12

ftNj
e )1(2

. . . . .

LNTl
lNT
s
dt
/)1(
L
s/
l

{
0,1,…,L
-
1
}
l

{
0,1,…,L
-
1
}
l

{0,1,…,L-1}
. . . . .

LNT
L
s
s
dt
/
/
l
lNT
)1(

LNTl
L
lNT
s
dt
/)1(
/
1
l
r
1N
l
r
Combining over time components
Decision
Device
b
ˆ
Parallel to Serial
C
opyright © 2010 SciRes. WSN

P. K. TEH ET AL. 192
 nnnb
NT
L
rn
l
n
l
s n
l,][
2
1

,...,1,0{},1,...,1,0{ LlN }1 (17)
where is a zero-mean Gaussian random variables
with variance No/2. The first term in (17) represents lth 
nth component of the desired signal and the second term
is noise. With N  L diversity com, N over fre-
quency a over time, the combiner can be design to
utilize dit combining techniques such as Equal
Gain Coming (EGC) or Maximumo Combining
(MRC) (in single user environmentum Mean
Square Error Combining (MMSEC) leads to a similar
result as MRC).
2) BPS/MC-OFDM: Here, we co= 0 in (3) and
we ignore pulse shaping function
n
l
n
ponents
nd L
fferen
bin Rati
, Minim
nsider i
)(
t
g
s
NT . The MC-OF-
DM transmitted signal corresponds to
 ,)(2cos][)(
1
0
1
0
0





N
k
N
n
o
n
ktfnfkbts

t],0[ s NT
(18)
This signal is applied to the antenna array in Figure 3
and the output of the mth element of the atenna array is
given by,
n


,)()(2cos][( o
n
km tmtfnfkbs
 )
1 1 


N N
t
0 0k n
}1,...,1,0{],,0[  MmNTt s (19)
Considering all antenna elements (all m), the total
normalized downlink transmitted signal is









1
0
1
0
1
0
)()(2cos
1
][)(
N
k
M
m
o
n
k
N
n
tmtfnf
M
nbts 
],0[ s NTt  (20)
Again, in (20) the frequency offset induced by  (t) in
the transmitted signal is minimal a ignored, since
the range of the control parameter  <
nd it is
0.05 in (6) creates
less than 5% bandwidth expansion. At the receiver, since
the transmit diversity leads to an L-fold time diversity,
the received signal can be divided into time slots [lNTs/L,
(l+1)NTs/L], l {0,1,…,L-1} and each individua
de
l slot
monstrates independent fades. The received signal can
be represented as
  

1N



1
00
1
0
)(2cos
1
][)(
M
m
o
k
N
n
n
k
n
ll tfnf
M
nbtr 

]/)1(,/[)(),( LNTlLlNTttntm ssl
n
l

w
l the nth
sub-carrier in the lth time slots, and

l
n is the fading phase
offset in the nth sub-carrier in the lth time slot (hereafter,
this phase offset is assumedo be tracked and removed).
The Rayleigh fade amplitudes, 
l
n, are independent over
time (l) and correlated over sub-carriers (n) with the cor-
relation coefficient between sub-carriers and
rized b4). Applying the summation over m,
(21) correspond
(21)
here, nl(t) is an additive white Gaussian noise (AWGN),
which is considered independent for different time slots
(l), 
n is the Rayleigh fade amplitude on
t
'n''n
charactey (1
s to

n
lb
 (2cos 






1
0
1
0
)),(][)(
N
k
o
n
k
N
n
ltfnftntr
 AF
)(),t 
of
(
2
1tn M
l



 
  (22)
structure BPS/MC-OFDM receiver is shown in
Figure 7 (Fure 7(b) represents jth bit receiver). The
received signal for each sub-carrier, n and time slot l can
be represented by
The
ig











1
0
][
2
1
][
2
1
][
N
jk
k
n
j
n
k
n
l
s n
l
s n
lkb
NT
L
jb
NT
L
jr 
}1,...,1,0{},1,...,1,0{,  LlNnnn
l (23)
where nl
n is a zero-mean Gaussian random variables with
variance No/2. In (23), the first term represent the desired
signal, the seco
ce and the t
is
2) Maximum Ratio Combining (MRC)
(2)
3) Minimum Mean Square Error Combining (MMSEC)
nd term represents the inter-bit-interferen-
hird term represents the noise. The factor 1/L
the direct consequence of dividing the received signal
into L partitions creating L-fold time diversity. The com-
biner can be designed to utilize different combining
techniques in frequency and time domain. Different
combining methods in frequency domain are:
1) Equal Gain Combining (EGC)



1
0
,
N
n
n
lEGClrR , (24)



1
0
,
N
n
n
l
n
lMRCl rR

, 5













 1
00
2
,
2
)(
N
nn
l
n
l
n
lMMSECl N
N
rR


(26)
Here, we present only Equal Gain Combining (EGC) in
the time domain to exploit the diversity induced by BPS.
4. Simulated Performance
Simulations are provided for MC-OFDM systems with
antenna arrays. The assumptions for these simulations
are as follow: 1) N = 32 sub-carriers in the MC-OFDM
system; 2) L = 7 independent fades are achievable as a
result of the beam-pattern movement in the duration NTs
C
opyright © 2010 SciRes. WSN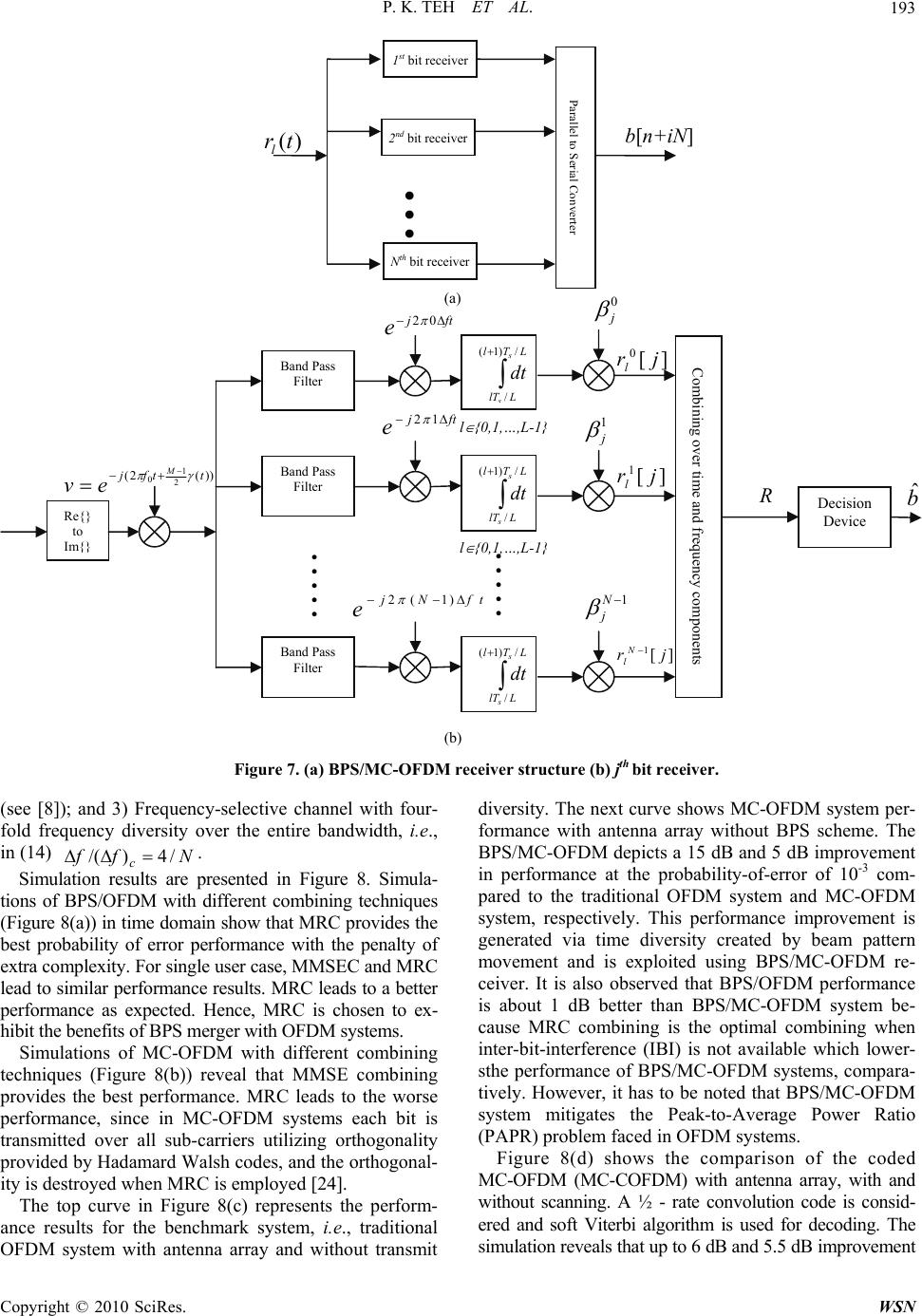

P. K. TEH ET AL. 193
(see [8]); and 3) Frequency-selective channel with four-
fold frequency diversity over the entire bandwidth, i.e.,
in (14)
Simulation results are presented in Figure 8. Simula-
tions of BPS/OFDM with different combining techniques
(Figure 8(a)) in time domain show that MRC provides the
best probability of error performance with the penalty of
extra complexity. For single user case, MMSEC and MRC
lead to similar performance results. MRC leads to a better
performance as expected. Hence, MRC is chosen to ex-
hibit the benefits of BPS merger with OFDM systems.
Simulations of MC-OFDM with different combining
techniques (Figure 8(b)) reveal that MMSE combining
provides the best performance. MRC leads to the worse
performance, since in MC-OFDM systems each bit is
transmitted over all sub-carriers utilizing orthogonality
provided by Hadamard Walsh codes, and the orthogonal-
ity is destroyed when MRC is employed [24].
The top curve in Figure 8(c) represents the perform-
ance results for the benchmark system, i.e., traditional
OFDM system with antenna array and without transmit
diversity. The next curve shows MC-OFDM system per-
formance with antenna array without BPS scheme. The
BPS/MC-OFDM depicts a 15 dB and 5 dB improvement
in performance at the probability-of-error of 10-3 com-
pared to the traditional OFDM system and MC-OFDM
system, respectively. This performance improvement is
generated via time diversity created by beam pattern
movement and is exploited using BPS/MC-OFDM re-
ceiver. It is also observed that BPS/OFDM performance
is about 1 dB better than BPS/MC-OFDM system be-
cause MRC combining is the optimal combining when
inter-bit-interference (IBI) is not available which lower-
sthe performance of BPS/MC-OFDM systems, compara-
tively. However, it has to be noted that BPS/MC-OFDM
system mitigates the Peak-to-Average Power Ratio
(PAPR) problem faced in OFDM systems.
Figure 8(d) shows the comparison of the coded
MC-OFDM (MC-COFDM) with antenna array, with and
without scanning. A ½ - rate convolution code is consid-
ered and soft Viterbi algorithm is used for decoding. The
simulation reveals that up to 6 dB and 5.5 dB improvement
Figure 7. (a) BPS/MC-OFDM receiver structure (b) jth bit receiver.
(b)
Nffc/4)/(  .
(a)
2nd bit receiver
Parallel to Serial Crteronve
st
1 bit receiver
)(trlb[n+iN]
...
Nth bit receiver
l

{
0
,
1
,
…
,
L-1
}
Combinin
g
over time and fre
q
uenc
y
com
p
onents
Decision
Device
b
ˆ
R
Re{}
to
Im
{}
)
)
(2(2
1
0ttfj M
ev




. . . . .
Band Pass
Filter
l

{
0
,
1
,
…
,
L-1
}
. . . . .

LTl
L
l
T
s
s
dt
/)1(
/
][
1jrl
j

1
ftj
e12

Band Pass
Filter 
LTl
L
l
T
s
s
dt
/)1(
/
ftj
e 02

l
0

][
0jr
j
Band Pass
Filter
tfNj
e )1(2


LTl
L
l
T
s
s
dt
/)1(
/
][
1jr N
l

1N
j

C
opyright © 2010 SciRes. WSN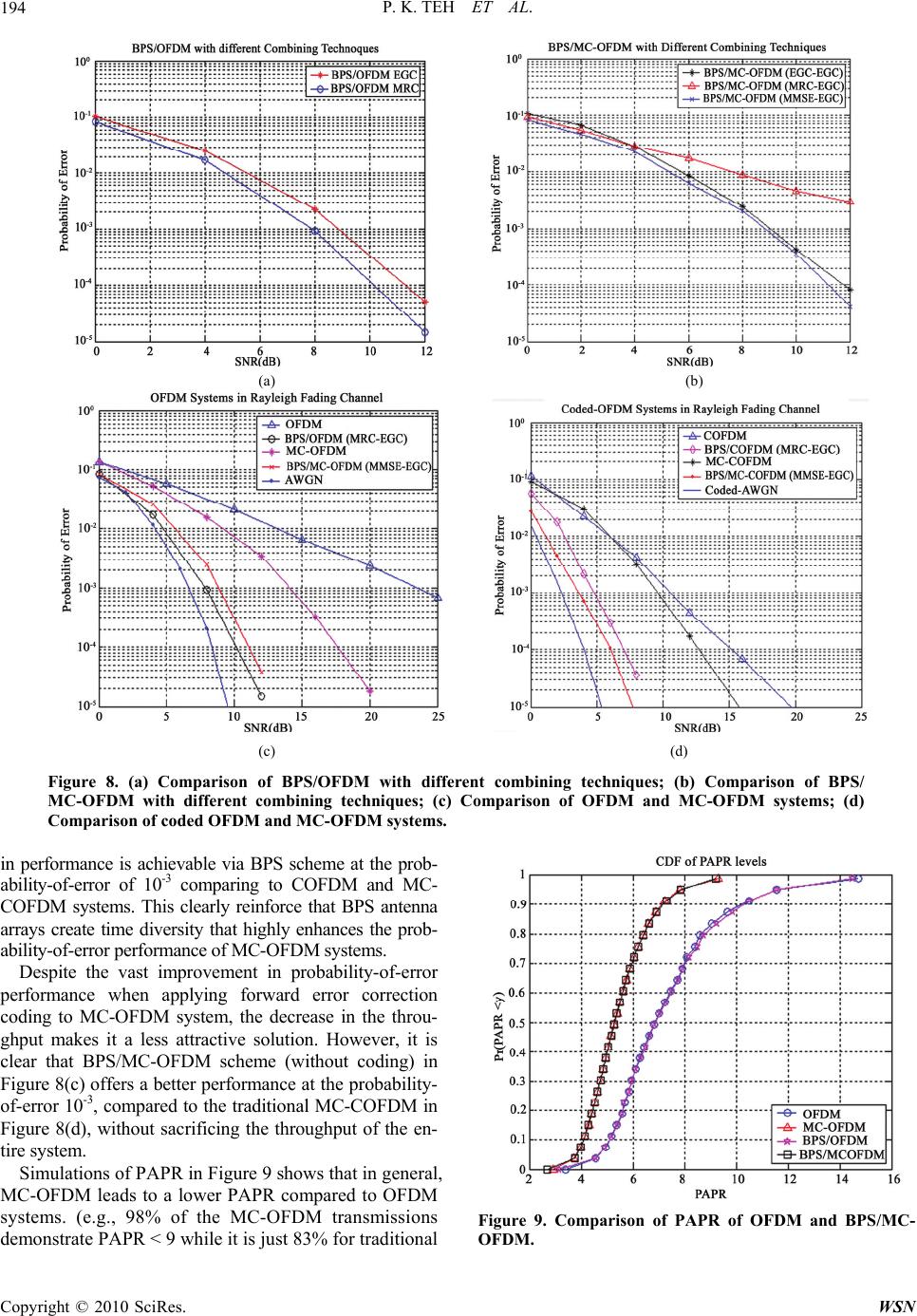

P. K. TEH ET AL. 194
(a) (b)
(c) (d)
Figure 8. (a) Comparisison of BPS/
C
ab
on of BPS/OFDM with different combining techniques; (b) Compar
MC-OFDM with different combining techniques; (c)
Comparison of coded OFDM and MC-OFDM systems.
in perforble via
omparison of OFDM and MC-OFDM systems; (d)
C-OFDM leads to a lower PAPR compared to OFDM
systems. (e.g., 98% of the MC-OFDM transmissions
demonstrate PAPR < 9 while it is just 83% for traditional
mance is achievaBPS scheme at the prob-
ility-of-error of 10-3 comparing to COFDM and MC-
COFDM systems. This clearly reinforce that BPS antenna
arrays create time diversity that highly enhances the prob-
ability-of-error performance of MC-OFDM systems.
Despite the vast improvement in probability-of-error
performance when applying forward error correction
coding to MC-OFDM system, the decrease in the throu-
ghput makes it a less attractive solution. However, it is
clear that BPS/MC-OFDM scheme (without coding) in
Figure 8(c) offers a better performance at the probability-
of-error 10-3, compared to the traditional MC-COFDM in
Figure 8(d), without sacrificing the throughput of the en-
tire system.
Simulations of PAPR in Figure 9 shows that in general,
M
Figure 9. Comparison of PAPR of OFDM and BPS/MC-
OFDM.
C
opyright © 2010 SciRes. WSN

P. K. TEH ET AL.195
OFDM systems). The same results are generated for
BPS/MC-OFDM systems. The simulations had proven
that BPS and MC-OFDM merger is a superior technique
capable of delivering high probability-of-error perform-
ance as well as reducing the PAPR problem in traditional
OFDM systems. This introduces BPS merger with MC-
OFDM as a very attractive scheme for future generations
of wireless communication systems.
6. Conclusions
The merger of BPS and MC-OFDM (BPS/MC-OFDM)
was introduced and the PAPR together with the probabil-
ity-of-error performance was studied. Time diversity is
created using BPS scheme that highly enhances the prob
ability-of-error performance of
Moreover, the inherent unique transmission method of
MC-OFDM lowers the PAPR problem compared to tradi-
tional OFDM system. This makes BPS/MC-OFDM
merger a very competitive technique in wireless commu-
nications. The simulations performed also reveal that bet-
ter performance is achievable via BPS/MC-OFDM (with-
out coding) compared to MC-COFDM without reducing
the throughput of the system inherent in MC-COFDM sys-
tems. The cost of deploying BPS/MCOFDM system is
minimal due to the fact that the complexity of BPS system
is mainly at the base station and the receiver complexity
itself is minimal because the diversity components enter the
receiver serially in time. Therefore, major improvement in
performance at a minimal cost makes BPS/MC-OFDM a
promising candidate for future wireless systems.
7. References
[1] R
c
2
.
1123–1134, July 2003.
[7] B. Natarajan, C. R. Nassar, S. Shattil, Z. Wu, and M.
Michelini, “High performance MC-CDMA via carrier in-
terferometry codes,” IEEE Transactions on Vehicular
Technology, Vol. 50, No. 6, pp. 1344–1353, November
2001.
[8] P. K. Teh and S. A. Zekavat, “Merging multi-carrier
OFDM and beam pattern scanning smart antennas:
achieving low PAPR, high performance and high direc-
tionality,” Proceedings 2003 Wireless Networking Sym-
posium, The University of Texas at Austin, October
22–24, 2003.
[9] Y. G. Li, J. Chuang, and N. R. Sollenberger, “Transmit
diversity for OFDM systems and its impact on high-rate
data wireless networks,” IEEE Journal of Selected Areas
in Communications, Vol. 17, pp. 1233–1243, July
. Naguib, and N. Seshadri,
“Space-time coded OFDM for high data rate wireless
communication over wideband channels,” in Proceedings
48th IEEE Vehicular Technology Conference, pp.
2232–2236, Ottawa, Canada, 18–21 May 1998.
[11] O. Norklit, P. C. F. Eggers, and J. B. Anderson, “Jitter
diversity in multipath environments,” IEEE 45th Vehicu-
lar Technology Conference, VTC’95, Vol. 2, pp. 853–
857, 25–28 July 1995.
[12] W. C. Wong, R. Steele, B. Glance, and D. Horn, “Time
diversity with adaptive error detection to combat rayleigh
fading in digital mobile radio,” IEEE Transactions on
Communications, Vol. COM-31, No. 3, pp. 378–387,
March 1983.
[13] S. A. Zekavat and C. R. Nassar, “Antenna arrays with
oscillating beam patterns: characterization of transmit di-
versity using semi-elliptic coverage geometric-ba
IEEE Transactions on Com-
, pp. 1549–1556, October
acity
wireless by merging multi-carrier CDMA systems and
oscillating-beam smart antenna arrays,” IEEE Transac-
tions on Vehicular Technology, Vol. 52, No. 4, pp. 772–
778, July 2003.
[15] S. A. Zekavat, C. R. Nassar, and S. Shattil, “Oscillating
beam adaptive antennas and multi-carrier systems:
Achieving transmit diversity, frequency diversity and di-
rectionality,” IEEE Transactions on Vehicular Technol-
ogy, Vol. 51, No. 5, pp. 1030 –1039, September 2002.
[16] A. M. Sayeed and B. Azhang, “Joint multipath-doppler
diversity in mobile wireless communications,” IEEE
Transactions on Communications, Vol. 47, No. 1, pp.
123–132, January 1999.
[17] J. C. Liberti, Jr., and T. S. Rappaport, “Smart antennas
for wireless communications: Is-95 and third generation
CDMA applications,” Prentice Hall, PTR, Upper Saddle
River, NJ, 1999.
[18] J. Fuhl, A. Kuchar, and E. Bonek, “Capacity increase
2–1966, 1997.
- 1999.
MC-OFDM systems. [10] D. Agarwal, V. Tarokh, A
. V. Nee and R. Prasad, “OFDM for wireless multimedia
ommunications,” Artech House Publisher, Boston, MA.
000.
2002.
[14] S. A. Zekavat and C. R. Nassar, “Achieving high cap
[2] S. B. Weinstein and P. M. Ebert, “Data transmission by
frequency-division multiplexing using the discrete fourier
transform,” IEEE Transactions on Communications, Vol.
COM-19, No. 5, pp. 628–634, 1971.
[3] L. J. Cimini and Jr., “Analysis and simulation of a digital
mobile channel using orthogonal frequency division mul-
tiplexing,” IEEE Transactions on Communications, Vol.
COM-33, No.7, pp. 665–675, 1985.
[4] R. W. Chang, “Orthogonal frequency division multiplex-
ing,” U.S. Patent 3, pp. 488–445, filed 1966, issued Janu-
ary 6, 1970.
[5] Z. Wang and G. B. Giannakis, “Wireless multicarrier
communications: where fourier meets shannon,” IEEE
Signal Processing Magazine, Vol. 17, No. 3, pp. 29–48,
May 2000
[6] D. A. Wiegandt, Z. Wu, and C. R. Nassar, “High-
throughput, high-performance OFDM via pseudo-
orthogonal carrier interferometry spreading codes,” IEEE
Transactions on Communications, Vol. 51, No. 7, pp.
sed sto-
chastic channel modeling,”
munications, Vol. 50, No. 10
in
cellular PCS by smart antennas,” IEEE 47th Vehicular
Technology Conference, VTC’97, Vol. 3, No. 10, pp.
196

P. K. TEH ET AL. 196
. Paulraj, and T. Kailath, “Capacity im-
base-station antenna arrays in cellular
assar, and S. Shattil, “Smart an-
Spread-Spectrum Technology, Vol. 2, pp.
[19] P. K. Teh and S. A. Zekavat, “A merger of OFDM and
antenna array Beam Pattern Scanning (BPS): achieving
directionality and transmit diversity,” Proceedings IEEE
37th Asilomar conference on Signals, Systems and Com-
puters, Asilomar, CA, November 9–12, 2003.
[20] A. Kavak, “Adaptive antenna arrays for downlink capac-
ity increase in third generation wireless CDMA,” in IEEE
Radio and Wireless Conference (RAWCON’01), pp.
77–80, Boston, MA, August 2001.
[21] A. F. Naguib, A
provement with
[23
CDMA,” IEEE Transactions on Vehicular Technology,
Vol. 43, No. 3, pp. 691–698, August 1994.
[22] S. A. Zekavat, C. R. N
tenna spatial sweeping for combined directionality and
transmit diversity,” Journal of Communications and Net-
works (JCN), Special Issue on Adaptive Antennas for
Wireless Communications, Vol. 2, No. 4, pp. 325–330,
December 2000.
] J. W. C. Jakes, “Microwave mobile communications,”
John Wiley, New York, NY, 1974.
[24] J. M. Auffray and J. F. Helard “Performance of multicar-
rier CDMA technique combined with space-time block
coding over rayleigh channel,” IEEE 7th International
Symposium on
348–352, 2–5 September 2002.