 Wireless Sensor Network, 2010, 2, 129-140 doi:10.4236/wsn.2010.22018 y 2010 (http://www.SciRP.org/journal/wsn/). Copyright © 2010 SciRes. WSN Published Online Februar Finding the Optimal Percentage of Cluster Heads from a New and Complete Mathematical Model on LEACH A. B. M. Alim Al Islam1, Chowdhury Sayeed Hyder2, Humayun Kabir3, Mahmuda Naznin4 1School of Electrical and Computer Engineering, Purdue University, West Lafayette, Indiana, USA 2Department of Computer Science and Engineering, Michigan State University, Michigan, USA 3,4Department of Computer Science and Engineering, Bangladesh University of Engineering and Technology, Dhaka, Bangladesh E-mail: abmalima@purdue.edu, hydercho@msu.edu, {mhkabir, mahmudanaznin}@cse.buet.ac.bd Received November 29, 2009; revised December 18, 2009; accepted December 21, 2009 Abstract Network lifetime is one of the important metrics that indicate the performance of a sensor network. Different techniques are used to elongate network lifetime. Among them, clustering is one of the popular techniques. LEACH (Low-Energy Adaptive Clustering Hierarchy) is one of the most widely cited clustering solutions due to its simplicity and effectiveness. LEACH has several parameters that can be tuned to get better performance. Percentage of cluster heads is one such important parameter which affects the network lifetime significantly. At present it is hard to find the optimum value for the percentage of cluster head parameter due to the absence of a complete mathematical model on LEACH. A complete mathematical model on LEACH can be used to tune other LEACH parameters in order to get better performance. In this paper, we formulate a new and complete mathematical model on LEACH. From this new mathematical model, we compute the value for the optimal percentage of cluster heads in order to increase the network lifetime. Simulation results verify both the correctness of our mathematical model and the effectiveness of computing the optimal percentage of cluster heads to increase the network lifetime. Categories and Subject Descriptors: [Sensor Networks] – Energy and resource management – Clustering. Keywords: Wireless Senor Network, Clustering, Mathematical Model Network Lifetime, Energy Consump- tion Rate, Renewal Reward Process 1. Introduction With the advent of new technology and low production costs, wireless sensor networks (WSN) prove to be useful in myriad of diversified applications, although its original development was motivated by military applications, such as battlefield surveillance. Most of the WSN applications involve monitoring, tracking, or controlling. Habitat monitoring, object tracking, nuclear reactor control, fire detection, and traffic monitoring are few examples of such WSN applications. In a typical WSN application, sensor nodes are scattered in a region from where they collect data to achieve certain goals. Data collection may be continuous, periodic or event based process. Irrespective of data collection process different kinds of management, such as power management, dynamic topology (due to node failure) management, self-config- uration management, resource management, and security management are necessary for WSN. Power management deals with the optimum energy usage in order to increase network lifetime. Dynamic topology management dyna- mically adjusts the topology in case of the death of an existing node or the arrival of a new node. Self configuration management enables the nodes to tune its parameters on the fly. Resource management takes the role to ensure effective resource (CPU and memory) shar- ing among multiple tasks. Security management guaran- tees protection against any theft or intrusion in the net- work. The importance of power management in WSN lies in the fact that the sensor nodes come with limited powered battery pre-installed. Moreover, the batteries cannot be replaced in the sensor nodes once they are in operation. For these reasons, the algorithms and protocols used in WSN have to be energy efficient. Different techniques are used to achieve energy efficiency like clustering, data  A. B. M. ALIM AL ISLAM ET AL. Copyright © 2010 SciRes. WSN 130 compression, dynamic power management etc. Among these, clustering techniques have got wider popularity. In clustering technique, deployed sensor nodes form some groups called clusters. Each cluster has only one cluster head node, which has the sole responsibility of communicating with the base station. Other nodes in a cluster are called followers. They collect and pass data to the corresponding cluster head. The cluster head of a cluster aggregates its own data with that of its followers. Aggregated data is then sent to one or more sinks. Compared to a sink, a cluster head generally remains closer to the followers. For this reason, it takes less energy to transmit data to the cluster head instead of transmitting directly to the sink. This allows the sensor nodes to conserve more energy and live longer in WSN. There are many clustering techniques [1–7], and [8] available in the literature. LEACH [1] is one of the simple but popular clustering techniques used in WSN. LEACH rotates the cluster head role very effectively among the sensor nodes of a cluster based only on some locally available infor- mation. Some modified LEACH [9–12] have also been proposed. LEACH has some parameters that can be tuned to make it more effective. The percentage of cluster heads, which is an input to LEACH algorithm that indicates the overall percentage of sensor nodes that can become cluster head at any time, plays an important role to achieve optimal energy consumption goal in a WSN. However, it is difficult to get the optimum value for this parameter due to the absence of a complete mathematical model on LEACH. In the mathematical model of [11], total energy con- sumption in the sensor network is calculated against the transmission of only one frame. In the mathematical model in [13] and [14] total energy consumption in the sensor network is calculated during a single round. En- ergy consumption during a single round or a frame transmission does not reflect the true energy consumption of the sensor nodes in their lifetime. The long run or ex- pected rate of energy consumption truly reflects the en- ergy consumption of the sensor nodes in their lifetime as the lifetime is inversely related to the long run rate of energy consumption. However, none of the previous LEACH mathematical models [11,13], and [14] has computed long run rate of energy consumption by the sensor nodes, which made them incomplete and not useful. Therefore, it is necessary to derive a mathematical model based on long run rate of energy consumption in the sensor nodes in order to make it complete and useful to compute the tunable parameters, such as the percentage of cluster head. In this paper, we formulate a complete mathematical model based on long run rate of energy consumption in the sensor nodes that uses LEACH clustering algorithm. We use this new mathematical model to find the optimal value of percentage of cluster heads and to tune other LEACH parameters. In the next section, we briefly describe some related works. We analyze the behavior of a random LEACH node by simulation in Section 3. We devise a complete mathematical model to realize this behavior in Section 4. In Section 5, we prove the correctness of our proposed mathematical model. In Section 6 and Section 7, we conclude the paper and shed some lights on our future work respectively. 2. Related Works LEACH [1] introduced a simple mechanism for localized coordination and control for cluster set-up and operation. It also introduces the randomized rotation of the cluster heads and the corresponding clusters. LEACH is a self-organizing, and adaptive clustering protocol [1]. It dynamically creates clusters in order to distribute the energy load evenly among all of the sensor nodes. This algorithm needs time synchronization. Cluster heads are randomly rotated during each time interval. The resultant cluster heads directly communicate with the base station. In LEACH, the lifetime of the network is divided into some discrete, disjoint time intervals. Each interval is again subdivided into some subintervals as shown in Figure 1. LEACH algorithm uses the percentage of cluster head parameter to determine the number of subintervals in an interval. The number of subintervals is the inverse of the value of the above parameter and this value is set a priori to the algorithm. Each subinterval begins with an advertisement phase followed by a cluster set up phase. In the advertisement phase, each node independently decides whether to become a cluster head or not and advertise this information to its neighbors. In the cluster set-up phase, the clusters are organized based on the decisions made in the advertisement phase. Then a steady-state phase fol- lows. In this phase, the followers, i.e., the sensor nodes except cluster heads, sends data to the corresponding cluster head. The cluster heads accumulate and compress the received data with its own data. Cluster heads finally send the compressed data to the base station or sink. In order to minimize cluster establishment overhead, the duration of steady-state phase is kept longer than that of cluster set-up phase. At the very beginning of an advertisement phase, each node decides whether it wants to become a cluster head for the current round. This decision depends on the value of the percentage of cluster heads as well as the number of times the node has already become cluster head. A node n chooses a random number between 0 and 1 and computes Figure 1. Discrete and disjoint intervals in the whole network lifetime; discrete and disjoint subintervals in an interval.  A. B. M. ALIM AL ISLAM ET AL. 131 a threshold T(n) as follows: otherwise Gnif P rP P nT 0 1 mod1 )( where, P = the percentage of nodes that can become cluster heads at any time (e.g. P = 0.05); 1/P = the number of subintervals in an interval; r = the current subinterval; G = the set of nodes that have not been cluster heads yet in the current interval. Comparing the random number with this threshold, a node can be either a cluster head or a follower in any one of 1/P subintervals of an interval. If the picked random number is less than the threshold T(n), the node decides to become a cluster head. Otherwise, it decides to become a follower. At the first subinterval of an interval (r = 0), each node has a probability P to become a cluster head. The nodes that were cluster heads in the first subinterval cannot be cluster heads in the next (1/P – 1) subintervals of the same interval. Thus the probability that the re- maining nodes are becoming cluster heads is increasing after each round. After the completion of 1/P subintervals, a new interval will start and all the nodes are again equally eligible to become cluster head. Each node that has chosen itself as a cluster head in the current subinterval, broadcasts an advertisement message to the rest of the nodes in its neighborhood. The non-cluster-head nodes will choose the cluster to which it will belong in this subinterval. This decision is based on the received signal strength of the advertised messages from the nearby cluster head nodes. Assuming symmetric propagation channels, the cluster head whose advertise- ments have been heard with the largest signal strength will be selected by a non-cluster-head sensor node as its cluster head. A cluster head is chosen randomly in case of a tie. This algorithm introduced a fairly simple strategy which is more efficient than the direct transmission. LEACH algorithm is also more effective than that of the minimum-transmission-energy (MTE) protocol, where minimum energy route is chosen to transmit data from the sensor nodes to the sink. LEACH algorithm uses the de- sired percentage of cluster heads as an input parameter. However, it is difficult to find the value of this parameter, for which LEACH will ensure optimum energy con- sumption. When the number of live sensor nodes becomes very small the number of prospective cluster heads, which is equal to the multiple of the number of live sensor nodes and the desired percentage of cluster heads, will also become very small and sometime it may become even less than one. For example, if the initial number of sensor nodes is 100 and the desired percentage of heads P is 0.05 then the initial number of prospective heads is 5 (=100×0.05). However, with the same P when the number of live nodes becomes less than 20 the number of prospective heads becomes less than one. Under this condition, none of the live sensor nodes can become a cluster head in most of the subintervals by choosing a random number less than the current threshold. In other words, there will be no cluster head available to the sensor nodes to which they can become followers. Rather, all the live sensors will force themselves to become a one member cluster head. In this particular case, the resultant cluster setting will behave like a setting which does not have clustering at all. For this reason, no energy efficiency will be gained. Despite of these limitations, LEACH is still a widely accepted clustering protocol and a number of its variants have already been proposed for further enhancement in [9–11], and [12]. SEP [9], a LEACH variant, modifies the equation of the threshold, T(n). Deterministic Cluster Head Selection [10], another variant of LEACH also modifies the threshold to accommodate the heterogeneity of resid- ual energy based on some heuristics. LEACH-C, proposed by the original LEACH authors in [11], is a centralized technique which selects the cluster heads based on their positions. It considers uniform distribution of the cluster heads based on their positions and the average residual energy in the network. Adaptive Cluster Head Selection [12], a distributed clustering technique based on LEACH, considers the positions for uniform distribution of cluster heads throughout the network. The availability of many variations on LEACH also indicates its popularity. Actu- ally, LEACH is very popular clustering technique because of its simplicity and effectiveness. There are some incomplete mathematical models available on LEACH. In [11], a mathematical model is proposed to compute the total energy dissipation in the sensor network for the transmission of a frame. By taking the derivative of the total energy it finds the optimum number of clusters, kopt as— 2 2BS mp fs opt d MN k where, N is the total number of sensor nodes, M is the dimension of the sensor area, dBS is the distance between cluster head and base station, fs and mp are the am- plifier energies. In [13], a mathematical model is proposed to compute the total energy consumption in the sensor network during a single round. By taking the derivative of the total energy, it also finds the optimum number of clusters, kopt as— 2 BS mp fs opt d MN k In [14], a mathematical model is proposed to calculate the total energy consumption in the sensor network during a single round. It also finds the desired optimum cluster head probability, popt as— C opyright © 2010 SciRes. WSN  A. B. M. ALIM AL ISLAM ET AL. Copyright © 2010 SciRes. WSN 132 DAelecBSmp fs opt EEd p 4 2 1 where, λ is the intensity of homogeneous spatial Poisson process that indicates the sensor node density, Eelec is the electronic energy required for coding, modulation, filtering etc. and EDA is the energy required for data aggregation. However, the lifetime of a sensor node is the inverse of its long run rate energy consumption. Therefore, in order to achieve elongated network lifetime of a sensor node, the long run rate of energy consumption must be more significant than the total energy consumption in an interval or for one frame transmission. Unfortunately, none of the mathematical models mentioned above consider the long run rate of energy consumption by a sensor node in the network. Moreover, none of these models consider the situation, in which all the sensor nodes in the network, can pick a random number higher than its respective threshold and become one member cluster head all together. For these reasons, all the previous mathematical models re- main incomplete and less useful. We deduce a complete mathematical model based on the long run rate of energy consumption and considering the above mentioned situa- tion in Section 4. In order to deduce the mathematical model, we need to observe the inherent behavior of a random LEACH node in terms of long run energy con- sumption. 3. Observed Behavior of A Random Leach Node In this section, we analyze the behavior of a random LEACH node in terms of long run energy consumption by simulation in order to find a trend in the behavior. In our simulation, expected energy consumption rate is calcu- lated against different percentage of cluster heads. A visual C++ program is developed for the simulation. We use following network setting as shown in the simu- lation runs: The dimension of sensor area is 200×200. Total number of heterogeneous sensor nodes in the network is 100. Initial energies of the sensor nodes are uniformly distributed between 1J and 5J. The sensor nodes are uniformly distributed over the sensor area. The base station is located at position (1500, 100). We show the network setting in Figure 2. We plot the energy consumption rate by a randomly chosen LEACH node against the percentage of heads in Figure 3 from the results of our simulation runs. According to the graph in Figure 3, 1) Energy consumption rate initially decreases very sharply with the increase of the percentage of cluster heads and 2) There is an optimal point for which energy con- sumption rate is the lowest. After the optimal point, the energy consumption rate increases with the increase of the percentage of cluster heads. In our simulation runs, this optimal point is (0.057, 0.003433). The pattern of the graph matches with that of the nor- malized energy dissipation versus the percentage of cluster heads in figure of [1]. We formulate a mathe- matical model complying with this behavior of a LEACH node in the next section. In Section 5, we compare the trends observed in this section with that from our mathematical model in order to proof that our mathe- matical model is correct and explain the reasons of these trends. 4. Proposed Mathematical Model for Leach The primary reason behind the clustering technique is to reduce the rate of energy consumption so that the life of a wireless network elongates. Popular clustering techniques leach [1] and its variants [9] and [10] can achieve this goal if their parameters are set suitably. As of today, some heuristics are used to choose the values for leach pa- rameters. A complete mathematical model can serve bet- ter than the heuristics to achieve an optimal rate of energy consumption in WSN. Moreover, a mathematical model can provide the ways to tune other application specific Figure 2. Uniformly distributed sensor network with a dis- tant base station. Figure 3. Energy consumption rate against different per- centage of heads for a randomly chosen leach node.  A. B. M. ALIM AL ISLAM ET AL.133 parameters. We derive a complete mathematical model of energy consumption rate of LEACH in this section. 4.1. Preliminaries We use some basic assumptions about the sensor nodes and the network settings while developing our mathe- matical model for LEACH. We also use some base mod- els in the formulation of our mathematical model. After describing the basic assumptions, we describe the base models. 1) Assumptions In order to make our mathematical model fully aligned with LEACH algorithm [1], we use following assump- tions about the sensor nodes and network settings: Nodes do not have any location information. This assumption makes our model suitable for the applications (for example, environmental monitoring) that use ran- domly deployed sensor nodes. All nodes can directly reach the BS. This assumption ensures applicability of our model for single-hop clus- tering [7]. The propagation channel is symmetric. Symmetry of propagation channel implies that energy required to transmit a message from node A to node B is the same as energy required to transmit a message from node B to node A for a given Signal to Noise Ratio (SNR). 2) Base Models Heinzelman proposed an energy model namely first order radio model for energy consumption in a wireless network in [15]. Like other research works [1], [9], and [10], we use this first order radio model to compute the expected energy consumption rate in sensor networks. Energy consumption, due to the reception and the transmission of data in a sensor network, is a stochastic process. Therefore, we use Renewal Reward Process [16], [17], a widely known stochastic process, to capture the nature of energy consumption due to data transmission and reception by a sensor node. In the following subsec- tions, we briefly describe these two base models. 3) Energy Model: Heinzelman First Order Radio Model A receiving sensor node consumes the energy while receiving and processing a message. The amount of this energy is proportional to the number of bits in the mes- sage under processing. For example, if the message con- tains k bit and the energy per bit is Eelec Joules, then the energy used to run the circuitry will be (Eelec×k) Joules. Therefore, the energy consumed by a receiving node to receive and process a k-bits message is, kEkE elecR X (1) The energy needs to send k bit message over a distance d is (amp x k×dλ) Joules, where amp is the energy con- stant for the radio transmission and λ is the path loss ex- ponent. While transmitting, a sensor node needs energy Figure 4. Heinzelman first order radio model. to process as well as to send the message. Therefore, the total energy consumed by a transmitting node to send a k-bits message over distance d is, dkkEdkE ampelecTX, (2) We consider Heinzelman’s first order model (i.e. λ = 2) for transmission of data in low noise environment. This model is shown in Figure 4. We consider λ = 4 for high noise environment. 4) Renewal Reward Process A Renewal Process is special counting process N(t) which counts the number of events up to time t and the inter-arrival times of the events are independent and identically distributed (iid) random variables. The ex- pected value of inter-arrival times is in between zero and infinity. A Renewal Reward Process [16,17] is a Renewal Process such that there are some rewards for each of the inter-arrival times. These rewards are also independent and identically distributed (iid) random variables. If Xi is the ith inter-arrival time and Ri is reward for the in- ter-arrival time Xi, the total reward earned up to time t will be: tN i i RtR 1 (3) According to Renewal Reward Theorem, the rate of reward will be: XE RE t tR t lim (4) This means that the rate of reward is equal to the ratio between the expected reward in a single inter arrival time E(R) and the expected inter-arrival time E(X) in the long run. The theorem can be proved based on Strong Law of Large Numbers [18] and is out of scope of the this paper. In stochastic process, the inter arrival time is also called a cycle. 4.2. Proposed Mathematical Model As the part of our mathematical analysis, we calculate the expected energy consumption rate following the re- Copyright © 2010 SciRes. WSN  A. B. M. ALIM AL ISLAM ET AL. Copyright © 2010 SciRes. WSN 134 newal-reward process. We consider the energy consumed by the sensor as the reward. Then the long run rate of reward will essentially be the long run rate of energy consumption. However, to map this problem with re- newal-reward process perfectly, we have to define cycle in such a way that both the reward and the cycle can be treated as iid random variables. According to LEACH algorithm, in the first subinterval of an interval each live sensor node will have some non zero probability to become cluster head. However, in the other subintervals a sensor node has zero probability to become cluster head, if it became a cluster head in the first or any other previous subinterval. It must be a follower in all other subsequent subintervals in the same interval. We define a cycle be the difference between two consecutive subintervals in which a sensor node becomes cluster head. Cluster establishment is probabilistically done in con- secutive subintervals. Hence, the cycle or inter-arrival time is an integer number and iid random variable. Energy consumption in each interval is also an iid random vari- able. These definitions of cycle and reward map our problem to a renewal-reward process perfectly. Thus, the long run rate of reward Equation (4) gives the expected energy consumption rate. We need to compute E(R) and E(X) to derive the energy consumption rate. We define following parameters for this purpose— 1) P is the desired percentage of cluster heads, 2) s is the number of subintervals in an interval, there- fore s = 1/P, 3) Ph is the probability of becoming cluster head of a follower node at the start of any subinterval, 4) Ph′ is the probability of becoming cluster head of a cluster head node at the start of a subinterval in the next interval, 5) Φ0 is the probability of becoming cluster head of a sensor node at the start of any subinterval, 6) Th is the currently considered threshold value. 7) N is the total number of sensor nodes in the network. 8) a × b is the two dimensions of rectangular sensor area. a) Calculation of E(X) We compute expected cycle length, E(X), of Equation (4) in this section. At the beginning of each subinterval new cluster heads are selected and new clusters are gen- erated. Each sensor will generate a random number be- tween 0 and 1 and compares it to a predefined threshold value Th. If the random number is less than the threshold, the sensor node becomes cluster head. Otherwise, the sensor node acts as a follower. We can show that the transitions between two states (heads: h and follower: f) of a sensor node while changing the subinterval in an inter- val by following matrix: hh PP f h fh 1 10 If the interval is changed then the probability of be- coming head while changing the subinterval will be the same irrespective of the previous state. Therefore, we can show the transitions between two states of a sensor node while changing the subinterval as well as the interval by following matrix: hh hh PP PP f h fh 1 1 Above behaviors of sensor nodes in LEACH can be shown by the transition diagrams in Figure 5. A sensor node can become cluster head at the start of the first subinterval of a new interval based on the picked random number and the threshold. This decision does not depend on whether it was cluster head or follower in the last subinterval of previous interval. In this case, the probability of a follower to become a cluster head and the probability of a cluster head to remain cluster head are same, i.e., Ph′ = Ph.. The number of subintervals in an interval is s. There- fore, a sensor node remains in the same interval up to (s-1) subinterval transitions and moves to the next interval only at the last subinterval transition. From this observation, we can say that the probability of remaining in the same interval is equal to (s-1)/s and the probability of changing the interval is equal to 1/s. We combine these probabilities with their corre- sponding transition matrices in order to capture the whole scenario. hh hh hh hh hh PP s Ps s P PP PP s PP s s 1 1 1 1 1 10 1(5) Hence, the combined transition matrix becomes as follows: 1) The probability of a cluster head to remain cluster head, Phh at the start of any subinterval is Ph/s. 2) The probability of a follower to become a cluster head, Phf at the start of any subinterval is Ph. (a) (b) Figure 5. State transition of a node while (a) Changing subinterval without changing Interval; (b) Changing sub- interval as well as the interval.  A. B. M. ALIM AL ISLAM ET AL.135 3) The probability of a cluster head to become a fol- lower, Pfh at the start of any subinterval is 1-Ph/s. 4) The probability of a follower to remain follower, Pff at the start of any subinterval is 1-Ph. Now, we can compute the probability of becoming a cluster head, Φ0, at the start of any subinterval by sum- ming up the first two values Phh and Phf as follows— s P sP s Ph h h1 0 (6) We can say that the expected value of the cycle is re- ciprocal of the probability of becoming cluster head, Φ0, at the start of any subinterval, i. e.— h Ps s XE 1 1 0 (7) In order to compute Ph we need to consider following two conditions— 1) A node can be a cluster head if the picked random number is lower than the threshold. In LEACH, the threshold is maintained in a way such that the mean value of the threshold becomes the percentage of sensor nodes to be elected as the cluster heads in the network. Hence, the probability of becoming cluster head in this way is equal to the said percentage, i.e., Ph1= P. 2) If none of the nodes pick the random number less than that of the threshold, all nodes act as one-member cluster head. The probability of becoming one-member cluster head in this way is, Ph2= (1 - P)N. Therefore, the ultimate probability of becoming a cluster head, Ph while changing subinterval in an interval will be P + (1 - P)N. Hence, expected cycle length E(X) can be calculated by substituting Ph from Equation (7). b) Calculation of E(R) We compute expected reward (energy consumption), E(R), of Equation (4) in this section. Energy consumption by a sensor node as a cluster head differs from that of a sensor node as a follower. Let— 1) H be the amount of energy consumed by a cluster head in a single subinterval and 2) F be the amount of energy consumed by a follower in a single subinterval. In a cycle, the expected number of subintervals in which a sensor node remains a follower is (E(X) – 1) and the expected number of subintervals in which a sensor node remains a cluster head is 1. Therefore, the amount of energy consumed by a sensor node in a single cycle is— HEFEXERE 1 (8) Here, E(F) and E(H) are the expected values of energy consumed by a follower and a cluster head, respectively, in a single subinterval. E(X) has already been calculated in previous sub-section. We need to calculate E(F) and E(H) in order to find E(R) of Equation (8). 1) Calculation of E(F) We can compute the expected value of energy, E(F), consumed by a follower in a single subinterval using Heinzelman first order radio model [15]. Being a follower, a sensor node consumes energy only for transmitting. According to Heinzelman First Order Radio Model, the total energy to transmit a k-bit message by a follower over distance X is— 2 _xkkExXFE Fampelec (9) If f(x) is the distribution function of the distance X of a follower to its nearest cluster head, the energy consump- tion by a follower will be— dxxfxkkE dxxfxkkE dxxfxheadclusternearestthetoanceDistFE FE Fampelec Fampelec 2 _ 2 _ (10) Now, we calculate the distribution function of the dis- tance, f(x)— xXP dx d xf (11) There might be several cluster heads at the nearest distance. Therefore, )(1 )(1 )1( xradiuswithareatheoutsideareheadsclusterallP xradiuswithareatheinsideisheadclusternoP xthanlessorxofancetdisatisheadclusterleastatPxXP (12) Now, if the number of cluster heads is Nc then, N n n nN h n h N n cc ab x P s s P s s n N nNPnNxoutsideareheadsclusterallP xradiuswithareatheoutsideareheadsclusterallP 1 2 1 2 1 1 1 1 (13) Therefore, we can calculate the distribution function of the distance, f(x) as follows— N n n nN h N n n h ab x xng ab x ab xn P s s P s s n N xXP dx d xf 1 1 2 2 1 1 1 21 1 1 (14 ) where, ab n P s s P s s n N ng nN h n h 2 1 1 1 Let, N n n dx ab x xng dxxfxI 1 1 2 3 2 1 (15) After solving the integration at the right side of the Copyright © 2010 SciRes. WSN  A. B. M. ALIM AL ISLAM ET AL. Copyright © 2010 SciRes. WSN 136 above equation, we get— N n nn n y n y ng ab I 1 1 2 12 1 (16) where, ab x y 2 1 The subtracted value of y indicates the proportion be- tween two areas of Figure 6. Here, the first area is the area inside the circle with the center at the sensor node under consideration and the radius equal to the distance from the sensor node to its nearest cluster head. The second area is the total area covered by all the sensor nodes. If the cluster head position coincides with that of the node, we get the lower limit of x and ab x2 equal to zero. In this case, y value becomes 1. If the cluster head is positioned at a position such that the first area fully covers the second area, we get the higher limit of x and ab x2 equal to 1. In this case, y value becomes 0. Therefore, the integrated value with the limits of y is— N nnn ng ab I 1 2 0 11 11 2 1 (17) Combining Equations (10) and (17), we get the ex- pected value of energy consumption of a sensor node as a follower in a subinterval as follows— N n Fampelec nn ng ab kkEFE 1 2 _1 11 2 1 )( (18) 2) Calculation of E(H) We can compute the expected value of energy, E(H), consumed by a cluster head in a single subinterval using Equation (2). The cluster head aggregates and compresses the data from its followers with its own data before sending them to the base station. Therefore, the actual number of Figure 6. y is the ratio between two areas. First one is the remaining area under consideration and the second one is the total area under consideration. bits sent by a cluster head is less than the summation of the numbers of the bits of all the messages those it handles. Let, γ be the compression ratio. If there are Nf followers and each sensor node generates k bit message, the energy consumption by a cluster head will be: BSHampfDAelecff dkNEEkNNHE _ 112 (19) where, dBS is the distance between the cluster head and base station. Now, 1 0 _ 1 0 112 )( N i fBSHampDAelec N i ff iNPdkiEEki iNPiNHEHE (20) Since Nc is the total number of cluster heads we can write, iN n CCff nNPnNiNPiNP 1 (21) Here, nN n Cn N nNP 00 1 (22) and inNi Cf APAP i nN nNiNP 1 (23) Here, A is an event that ensures the considered cluster head is the nearest cluster head to a follower. If the loca- tion of the cluster head is (xh, yh) and the location of the follower is (x, y), we can write 1 22 1 n aa p ab r p ab r AP (24) where, r = √((x - xh)2 + (y - yh)2) and pa is the percentage of the circular area (centered at the follower and with radius r) falls within the area covered by the sensor net- work. Let, P(A)=h(r, n). Now, combining Equations (21–23), we get— iN n nN n inNi fn N nrhnrh i nN iNP 1 00 1,1, (25) Combining Equations (6), (20) and (25), we get— N i BSHampDAelecdkiEEki HE 1 0 _ 112 iN n nN h n h inNi P s s P s s n N nrhnrh i nN 1 1 1 1 ,1, (26) c) Energy Consumption Rate Combining Equations (7), (8), (18) and (26),, we can get energy consumption rate as follows—  A. B. M. ALIM AL ISLAM ET AL.137 1 01 1 2 _ , 1 1 11 2 11 1 lim N i iN n h N n Fampelech t niqipP s s nn ng ab kkEP s s XE RE t tR (27) where, BSHampDAelec dkiEEkiip _ 112 and, N h n h inNiP s s P s s n N nrhnrh i nN niq 1 1 1 ,1,, Equation (27) concludes the formulation of our mathe- matical model. This equation evaluates the expected en- ergy consumption rate in a wireless sensor net- work. The optimal number of cluster heads can be determined using this equation by plotting various expected energy con- sumption rate against different percentage of cluster heads. The percentage of cluster heads at the lowest expected energy consumption rate gives the optimal percentage of cluster heads. In the next section, we prove the correctness of our analytical model by simulation results and also find the optimal percentage of cluster heads. 5. Simulation Results and Validation of Analytical Model Like [11,13,14], we cannot find the optimal value of percentage of cluster heads by taking derivative of the equation of long run rate of energy consumption as there is no closed form of the derivative of Equation (27). Therefore, to verify the correctness of our mathematical model, we conduct simulation runs with the previously described network settings and parameters. We use the following values of the parameters in the simulation runs to be aligned with the simulations of the research works in [1,10,19]— 1) The amount of energy per bit to run sensor node circuitry, Eelec is 5 x 10-8; 2) Both the values of energy constants, amp_F and amp_H for radio transmission, is 1 x 10-10; 3) A sensor node generates 0 to 50 units data in an in- terval; 4) Each data unit contains 8 bits data; 5) The probability that a message successfully arrives at its destination is 90%. Therefore, the communications are low noise and thus λ=2. We first calculate the lifetime of a sensor node as the number of subintervals it remains alive. We also calculate the energy consumption rate of a sensor node as the ratio between total energy and lifetime. Then, we calculate average lifetime and average energy consumption rate of the sensor nodes in the network from ten simulation runs and plot them in Figure 7(a) and Figure 7(b) accordingly. Figure 7(b) has the similar pattern that has been found in Figure 3. The optimal point is (0.048, 951.67) in Figure 7(a) and (0.044, 0.003082) in Figure 7(b). Apparently, the optimal percentage of cluster heads in both the graphs should be equal. However, in the simulation runs total energy of a sensor node is its initial energy which is uni- formly distributed between 1J and 5J. Therefore, total energies of the sensor nodes are different. As a result, optimal percentages of cluster heads in Figure 7(a) and Figure 7(b) are also different. These two percentages of cluster heads (0.044 and 0.048) roughly indicate the range in which the actual optimal percentage of cluster heads should lie. Before validating our mathematical model against the graphs found from simulation runs, we briefly illustrate the reason behind the trend in the graph of average en- ergy consumption rate against the percentage of cluster heads in Figure 3 and Figure 7(b). The percentage of cluster heads P reflects the expected value of the thresh- old. When the value of P is close to 0, the probability of the random numbers picked by the sensor nodes in the network to be less than the threshold becomes very low. In this situation, most of the sensor nodes will frequently become one member cluster head. Therefore, the ex- pected energy consumption rate becomes high. As the value of P increases, the probability of frequently be- coming one member cluster head for the sensor nodes decreases, i.e., the probability of becoming follower in- creases and the expected energy consumption rate de- creases. Though the probability of becoming a one member cluster head decreases with the increase in P after a certain point this does not help that much to re- duce the ultimate energy consumption rate. After that point the increase in the percentage of cluster heads in- creases the probability of the sensor nodes to become regular cluster head. This is superseding the energy sav- ings by not becoming one member cluster head. For this reason, as the value of the percentage of cluster heads increases the ultimate energy consumption rate increases. We plot the energy consumption rate against different percentage of cluster heads P using Equation (27) of our mathematical model for the same network settings and parameters in Figure 8(a). For high noise data communi- cation between cluster head and base station λ=4 is appli- cable. The resultant graph with λ=4 is also shown in Figure 8(b). In both the cases, the resultant graphs have the same trend which perfectly matches the trend found in Figure 7(b) by simulation. Moreover, the optimal point is (0.044, 0.003082) in Figure 7(b) and is (0.045, 0.003733) in Figure 8(b). These two optimal points match very closely. The value of the probability of becoming cluster head of a sensor node at the start of any subinterval Φ0 must not exceed 1 and the value of Φ0 can be computed from by Equation (6). According to Equation (6), if the value of P Copyright © 2010 SciRes. WSN 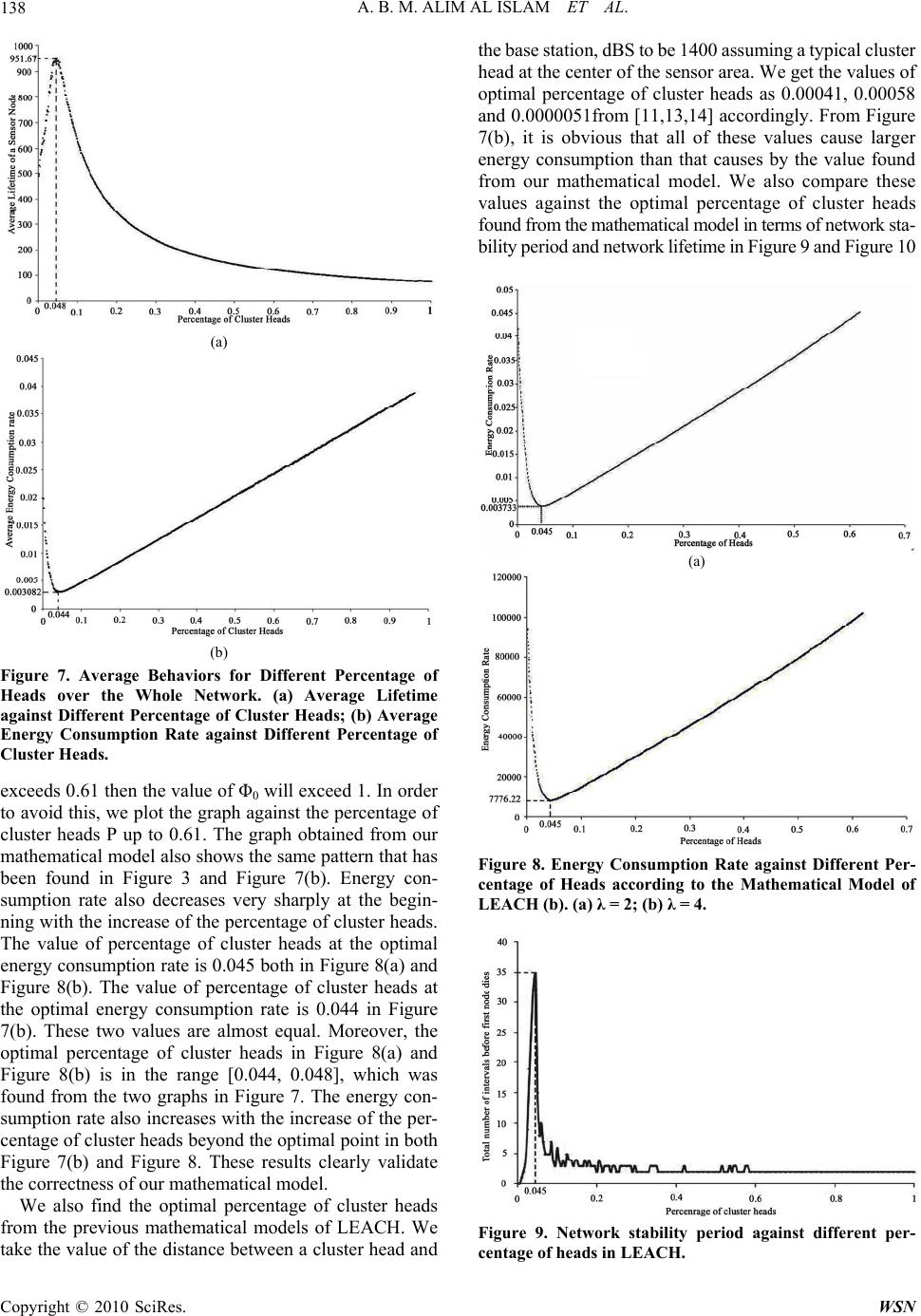 A. B. M. ALIM AL ISLAM ET AL. Copyright © 2010 SciRes. WSN 138 (a) (b) Figure 7. Average Behaviors for Different Percentage of Heads over the Whole Network. (a) Average Lifetime against Different Percentage of Cluster Heads; (b) Average Energy Consumption Rate against Different Percentage of Cluster Heads. exceeds 0.61 then the value of Φ0 will exceed 1. In order to avoid this, we plot the graph against the percentage of cluster heads P up to 0.61. The graph obtained from our mathematical model also shows the same pattern that has been found in Figure 3 and Figure 7(b). Energy con- sumption rate also decreases very sharply at the begin- ning with the increase of the percentage of cluster heads. The value of percentage of cluster heads at the optimal energy consumption rate is 0.045 both in Figure 8(a) and Figure 8(b). The value of percentage of cluster heads at the optimal energy consumption rate is 0.044 in Figure 7(b). These two values are almost equal. Moreover, the optimal percentage of cluster heads in Figure 8(a) and Figure 8(b) is in the range [0.044, 0.048], which was found from the two graphs in Figure 7. The energy con- sumption rate also increases with the increase of the per- centage of cluster heads beyond the optimal point in both Figure 7(b) and Figure 8. These results clearly validate the correctness of our mathematical model. We also find the optimal percentage of cluster heads from the previous mathematical models of LEACH. We take the value of the distance between a cluster head and the base station, dBS to be 1400 assuming a typical cluster head at the center of the sensor area. We get the values of optimal percentage of cluster heads as 0.00041, 0.00058 and 0.0000051from [11,13,14] accordingly. From Figure 7(b), it is obvious that all of these values cause larger energy consumption than that causes by the value found from our mathematical model. We also compare these values against the optimal percentage of cluster heads found from the mathematical model in terms of network sta- bility period and network lifetime in Figure 9 and Figure 10 (a) Figure 8. Energy Consumption Rate against Different Per- centage of Heads according to the Mathematical Model of LEACH (b). (a) λ = 2; (b) λ = 4. Figure 9. Network stability period against different per- centage of heads in LEACH.  A. B. M. ALIM AL ISLAM ET AL.139 Figure 10. Network lifetime against different percentage of heads in LEACH. accordingly. Network stability period is the number of intervals passed before the death of the first node and network lifetime is the number of intervals passed before the death of the last node. We plot the network stability period against different percentage of cluster heads in Figure 9. Here, we find the maximum network stability period at the point (0.045, 35). We also plot the network lifetime against different percentage of cluster heads in Figure 10 and find the maximum network lifetime at the point (0.045, 115). In both cases, the optimal percentage of cluster heads found from our mathematical model perfectly matches to the optimal points. However, all the optimal percentages of cluster heads found from the pre- vious mathematical models give significantly lower val- ues for both stability period and network lifetime. 6. Conclusions In this paper, we devised a mathematical model on LEACH protocol, a widely accepted clustering protocol for WSN. For the verification of our mathematical model, we have simulated a WSN with a random setting. We have applied our mathematical model on the same net- work setting. We have plotted two graphs of energy consumption rate versus the percentage of heads, one for each of the above cases. The conformity between these two graphs ensures the correctness of our mathematical model. We have also showed that we can find the optimal percentage of cluster heads, for which the energy con- sumption rate would be the lowest, from the graph of the mathematical model. 7. Future Works In this paper, we have proposed a mathematical model on the original LEACH, which does not consider the heterogeneity of the sensor nodes in terms of the residual energy and some other problems mentioned in Section 2. In our future work, we will modify basic LEACH algo- rithm and our mathematical model in order to incorpo- rate the above heterogeneity of the sensor nodes and to overcome problem exists in the original LEACH algo- rithm. 8 . References [1] W. B. Heinzelman, A. P. Chandrakasan, and H. Balakrishnan, “Energy efficient communication protocol for wireless microsensor networks,” In Proceedings of the Hawaii International Conference on System Sciences, Maui, Hawaii, Vol. 2, pp. 10, January2000. [2] S. Lindsey and C. S. Raghavendra, “PEGASIS: power- efficient gathering in sensor information systems,” Aero- space Conference Proceedings, Vol. 3, pp. 1125–1130, 2002. [3] L. Li, S. Dong, and X. Wen, “An energy efficient clustering routing algorithm for wireless sensor net- works,” The Journal of China Universities of Posts and Telecommunications, Vol. 3, No. 13, pp. 71–75, Sep- tember 2006. [4] Y. Sangho, H. Junyoung, C. Yookun, and H. Jiman, “PEACH: power-efficient and adaptive clustering hie- rarchy protocol for wireless sensor networks,” Com- puter communications, Vol. 30, pp. 2842–2852, 2007. [5] S. Ghiasi, A. Srivastava, X. Yang, and M. Sarrafzadeh, “Optimal energy aware clustering in sensor networks,” SENSORS Journal, Vol. 7, No. 2, pp. 258–269, 2002. [6] H. Chan and A. Perrig, “ACE: an emergent algorithm for highly uniform cluster formatio,” Lecture Notes in Computer Science, Springer Berlin/Heidelberg, Vol. 2920, pp. 154–171, February 2004. [7] O. Younis and S. Fahmy, “Distributed clustering in ad-hoc sensor networks: a hybrid, energy-efficient approach,” Proceedings of IEEE Infocom, Vol. 1, pp. 640, 2004. [8] J. Y. Cheng, S. J. Ruan, R. G. Cheng, and T. T. Hsu, “PADCP: poweraware dynamic clustering protocol for wireless sensor network,” International Conference on Wireless and Optical Communications Networks, pp. 6, 13 April 2006. [9] G. Smaragdakis, I. Matta, and A. Bestavros, “SEP: a stable election protocol for clustered heterogeneous wireless sensor networks,” In the Proceedings of the International Workshop on SANPA, 2004. [10] M. Haase and D. Timmermann, “Low energy adaptive clustering hierarchy with deterministic cluster-head selection,” 4th International Workshop on Mobile and Wireless Communications Network, pp. 368–372, 2002. [11] W. B. Heinzelman, A. P. Chandrakasan, and H. Balakrishnan, “An application-specific protocol archi- tecture for wireless microsensor networks,” IEEE Transa- ctions on Wireless Communications, pp. 660–670, Octo- ber 2002. [12] C. Nam, H. Jeong, and D. Shin, “The adaptive cluster head selection in wireless sensor networks,” IEEE International Workshop on Semantic Computing and Applications, pp. 147–149, 2008. Copyright © 2010 SciRes. WSN  A. B. M. ALIM AL ISLAM ET AL. Copyright © 2010 SciRes. WSN 140 [13] J. C. Choi and C. W. Lee, “Energy modeling for the cluster-based sensor networks,” In Proceedings of the Sixth IEEE International Conference on Computer and Information Technology, pp. 218, September 20–22 2006. [14] S. Selvakennedy and S. Sinnappan, “An energy-efficient clustering algorithm for multihop data gathering in wireless sensor networks,” Journal of Computers, pp. 1, April 2006. [15] W. B. Heinzelman, A. P. Chandrakasan, and H. Balakrishnan, “Energy efficient communication protocol for wireless microsensor networks,” In Proceedings of the Hawaii International Conference on System Sciences, Maui, Hawaii, January 2000. [16] E. Popova and H. C. Wu, “Renewal reward processes with fuzzy rewards and their applications to T-age replacement policies,” European Journal of Operational Research, Vol. 117, pp. 606–617, 1999. [17] R. Zhao and B. Liu, “Renewal process with fuzzy interarrival times and rewards,” International Journal of Uncertainty, Fuzziness and Knowledge based Systems, Vol. 11, pp. 573–586, 2003. [18] H. D. Brunk, “The strong law of large numbers,” Duke Mathematical Journal, Vol. 15, pp. 181–195, 1948. [19] http://www.xbow.com/Products/productdetails.aspx? sid= 156
|