J. Software Engineering & Applications, 2010, 3: 160-166
doi:10.4236/jsea.2010.32020 Published Online February 2010 (http://www.SciRP.org/journal/jsea)
Development of a Web-Based Decision Support System
for Cell Formation Problems Considering Alternative
Process Routings and Machine Sequences
Chin-Chih Chang
Department of Information Management, Jen-Teh Junior College of Medicine, Nursing and Management, Taiwan, China.
Received November 16th, 2009; revised December 3rd, 2009; accepted December 12th, 2009
ABSTRACT
In this study, we use the respective advantages of the tabu search (TS) and the Web-based technologies to develop a
Web-based decision support system (DSS) for cell formation (CF) problems considering alternative process routings
and machine sequences simultaneously. With the assistance of our developed Web-based system, the CF practitioners in
the production departments can interact with the systems without knowing the details of algorithms and can get the best
machine cells and part fa milies with minimize the to tal intercellu lar movemen t wherever and whenever th ey ma y need it.
To further verify the feasibility and effectiveness of the system developed, an example taken from the literature is ado-
pted for illustrationa l purpose. Moreover, a set of test problems with va rious sizes drawn from the literature is used to
test the performance of the proposed system. Corresponding results are compared to several well-known algorithms
previously published. The results indicate that the proposed system improves the best results found in the literature for
67% of the test problems. These show that the proposed syst em should t hus be usef ul to bot h practitioners and researchers.
Keywords: Web-Based, Cell Formation, Tabu Search, Decision Support System, Alternative Process Routings
1. Introduction
In response to various and diversified customer demands,
companies must adopt innovative manufacturing strate-
gies and manufacturing technologies to achieve an effi-
cient and flexible manufacturing system. Group technol-
ogy (GT) is one such approach that meets the require-
ments of system flexibility and product variations. GT is
a manufacturing philosophy, which determines and di-
vides the components into families and the machines into
cells by taking advantage of part similarity in processing
and design functions. Studies show that 30%–75% of the
product cost is due to materials handling [1]. Cellular
manufacturing (CM) is the application of group technol-
ogy (GT) in manufacturing systems. The implementation
of cellular manufacturing system (CMS) design has been
reported to result in significant benefits such as reduc-
tions in material handling costs, work-in-progress inven-
tory, throughput times and set-up times, simplified
scheduling and improved quality [2]. Cell formation (CF)
is the crucial element in de signing CMS. However, it has
been known that the CF in CMS is one of the NP-hard
combinational problems [3], as it becomes difficult to
obtain optimal solutions in an acceptable amount of time,
especially for large-sized problems. While considering
alternative process routings and machine sequences to
CF problems, making the problems more realistic; how-
ever, it leads to a more complex problem than the simple
CF problem. Thus, development of an effective com-
puter-aided manufacturing CF support system is neces-
sary. In this regard, many models and solution approa-
ches have been developed to identify machine cells and
part families. These approaches can be classified into
three main categories [4]: 1) mathematical programming
(MP) models [5–8], 2) heuristic/meta-heuristic solution
algorithms [9–11], and 3) similarity coefficient methods
(SCM) [12,13].
Due to their excellent performance in solving combi-
natorial optimization problems, meta-heuristic algorithms
such as genetic algorith m (GA), simulated annealing (SA)
and tabu search (TS) have been the most successful solu-
tion approach to efficiently solve the CF problem and its
variants with good results. Among the meta-heuristic
algorithms, TS has been successfully used to solve many
problems appeared in manufacturing system including
cell formation problems [14]. Hence, we adopt it as a
solver to solve the CF problem considering alternative

Development of a Web-Based Decision Support System for Cell Formation 161
Problems Considering Alternative Process Routings and Machine Sequences
process routings and machine sequences simultaneously
in the development of our CF Web-based decision sup-
port system (DSS).
In addition, CF algorithms are usually expressed in
mathematical terms, which may only be understood by
domain experts, but not by most of the CF practitioners
in the production departments. With the assistance of CF
DSS, users can interact with the systems without know-
ing the details of algorithms. Moreover, due to an in-
creasing global competition, companies are now shifting
to a geographically distributed manufacturing environ-
ment. Besides, the information flow nowadays requires
reliability, efficiency and security. With the emergence
of information technology, the traditional way of com-
munication of information flows between companies and
between internal parties can now be replaced by the in-
terconnected network [15]. The Internet provides an open
environment for companies to connect with their busi-
ness partners as well as to serve as a medium for internal
information flows [16]. Moreover, manufacturing sys-
tems have migrated to integrate with the Internet to pro-
vide a remote access and control system with the charac-
teristics of quick response and real line monitoring [17].
In this study, we use the respective advantages of the
TS and the Web-based technologies to develop a Web-
based DSS for CF problem considering alternative proc-
ess routings and machine sequences simultaneously. An
example taken from the literature is adopted for illustra-
tional purpose. To further v erify the feasibility and effec-
tiveness of the system developed, ten test problems with
various sizes drawn from the literature are used to test
the performance of our proposed CF so lver. Correspond-
ing results are compared to several well-known algo-
rithms previously published.
The remainder of this article is organized as follows:
Section 2 describes the problem definition including cell
formation and the mathematical model; Section 3 details
the implementation of our Web-based CF DSS; Section 4
verifies the performance of the proposed system and
methodology; and Section 5 concludes the paper.
2. Problem Definition
2.1 Cell Formation
In a simple CF problem, cell formation in a given 0–1
machine-part incidence matrix involves rearrangement of
rows and columns of the matrix to create part families
and machines cells, in which the cellular movement can
be minimized and the utilizatio n of the machin es within a
cell can be maximized. Two matrices shown in Figure 1
are used to illustrate the concept. Figure 1(a) is an initial
matrix where no blocks can be observed directly. After
rearrangement of rows and columns, two blocks can be
obtained along the diagonal of the solution matrix in
Figure 1(b). For those 1’s outside the diagonal blocks,
they are called “exceptional elements”; while those 0’s
inside the diagonal blocks are called “voids”.
When parts have alternative process routings (APR) is
called the generalized CF problem. Such as the case
shown in Table 1, part #1 has two process routings R1
and R2. Kusiak [5] first described the problem and pre-
sented an integer-programming model to solve the prob-
lem. While introducing APR to CF problems, the group-
ing of parts can be more effective due to the flexibility of
the routes; however, it leads to a more complex problem
than the simple CF problem. Under this circumstance,
not only the formation of part families and machine cells
must be determined but also the selection of routings for
each part has to be determined to achieve decision objec-
tives such as the minimizatio n of intercellular movement.
For instance, Table 2 provides a feasible solution to the
sample problem of Table 1 with a total intercellular mo-
vement of 215.
2.2 Mathematical Model
The decision objective of their research is to minimize
the sum of total intercellular movement. The 0–1 integer
programming model that they formulated is given below,
and the notations are introduced first.
Figure 1. Rearrangement of rows and columns of matrix to
create cells: (a) initial matrix and (b) matrix after rear-
rangement
Table 1. Initial machine-part matrix where alternative
process routings are allowed
PV: Production Volume; PN: Part Number; RN: Routing Number; *
Process Sequence

Development of a Web-Based Decision Support System for Cell Formation 162 Problems Considering Alternative Process Routings and Machine Sequences
P5 P6 P8 P1P2 P3 P4 P7
R1 R1 R2 R1R1 R1 R1 R1
M2 1 1 1
M6 2
M7 2 2
M1 11 1 1 1
M3 2 2
M4 22 3 2
M5 33 3 3
M8 3 4 4 4
M9 3 4 4
Figure 2. Final machine-part matrix of Table 1
Notations:
m Number of machines
p Number of parts
NC Number of cells
Vi Production volume for part i
Qi Number of routings for part i
Um Maximum number of machines in each cell
Lm Minimum number of machines in each cell
Kij
Number of operations in routing j of part i;
the operations of part i along route j are processed
on a machines’ set of

()(1)
(1) (2)() (1)
, ,..., ,,...,
,ijij KK
kk
ij ijijijij
ij
u
uu uuu




{1,2,..., } ip
m
NC
()k
ij
u Machine index for the k-th operation of part i along
route j
Ykl 1, if machine k locates in cell l; 0, otherwise
Zij 1, if routing j of part i selecte d; 0, otherwise
The 0–1 integer programming model is as follows:
Min (1)

1
(1)
() ()
()
11111
QK
pij
iNC
k
kij
ij
ijl l iu
l
u
ijkl Y
ICM Z
VY




 
st:
1
1



i
Q
j
ij
Z  (2)
11
NC
kl
lY 

 (3) {1,2, ...,}k
1
m
mkl m
kU
LY


 {1,2, ...,}l

 (4)

,,0,1 ,,,
kl ijijkl
YZ
 (5)
In the above model, Equations (1) is the objective
function, which show the calculation of the total inter-
cellular movement. Equation (2) indicates that only one
process routing will be assigned to each part. Equation (3)
provides a restriction that each machine will be assigned
to exactly one cell. Equation (4) assigns the upper and
lower limits of the cell size. Equation (5) indicates that
Ykl and Zij are 0–1 binary decision variables.
The large number of binary variables and constraints
makes it difficult to obtain optimal solutions in an ac-
ceptable amount of time. Developing an effective com-
puter-aided manufacturing CF support system is more
appropriate than using the exact method in terms of solu-
tion efficiency, especially for large-sized problems. This
paper, thus, presents an efficient Web-based DSS for CF
problem. The developed system is described and ex-
plained in detail in th e next section.
3. System Development
In this study, we dedicated to develop a Web-based CF
DSS. With this system, the users can upload the CF data
to Web serve and then with the CF solv er executed, they
can get the best machine cells and part families with
maximize grouping efficacy wherever and whenever they
may need it. The system architecture for CF DSS is
shown in Figure 3. From the figure, we can know that the
system consists of five elements. They are the clients (i.e.,
users), the Web-based user interface, the Web server, the
CF solver and the database. All of them are linked up
with the Internet but may be located in different geo-
graphical places. We will describe them below.
3.1 Client and Web-based User Interface
Web browsers are clients that connect to Web servers
and retrieve Web pages for display. Using appropriate
Web browsers, such as Netscape’s Navigator or Micro-
soft’s Internet Explorer, users can input data or view the
CF results through a dynamic hypertext user interface.
Because of the PHP is a widely-used general-purpose
scripting language that is especially suited for Web de-
velopment and can be embedded into HTML. Hence, we
use PHP to making dynamic and interactive Web pages
for the Web-based user interface which consists of three
buttons on the top of the screen. The framework of the
user interface is shown in Figure 4 which is simple and
Framework of Web-based user interface
Upload Data: The client users can upload production
data to Web serve by using this button. The production
Figure 3. System architecture for CF DSS

Development of a Web-Based Decision Support System for Cell Formation 163
Problems Considering Alternative Process Routings and Machine Sequences
Figure 4. Considered to be user-friendly, we will describe
them below
data are given through a text document readable with any
text viewer (*.txt).
Parameters Setting: The client users can set up the pa-
rameters for CF solver.
Solving: With this button be pressed, the CF solver
will be executed to minimize the total intercellular mo-
vement.
3.2 Web Server
The Web server is a computer that serves requested Web
pages. The Web server interacts with the individual us-
er’s Web browser and accepts external Hypertext Tran-
sfer Protocol (HTTP) requests from the browser. An Ap-
plication Programmer’s Interface (API) is distributed,
along with most of the commercially available browsers,
such as Netscape’s Navigator or Microsoft’s Internet
Explorer. Application programs, such as PHP, ASP and
JSP, can be written using these APIs to enhance the ca-
pabilities of a browser. Because of the Apache HTTP
Server has been the most popular Web server on the
Internet since April 1996. Therefore, we use the Apache
server as Web server in this study.
3.3 CF Solver
The CF solver was developed using Visual C++ pro-
gramming languages. It cons ists of two stages: the initial
solution construction and the improvements. The Single
Linkage Clustering Algorithm (SLCA) of McAuley [13]
is adapted in the first stage to produce good initial solu-
tions, while the TS continuously improves and generates
more effective solutions through the TS algorithm in the
second stage. The proposed generic framework for the
CF solver is shown in Figure 5 wh ich is actually consists
of the following seven steps:
1) Initialization of co mputational parameters;
2) Construction of initial solution;
3) Searching of improving neighborhood solutions;
4) Update of tabu list;
5) Update of better solutions found;
6) Check of timing for directing searching toward di-
versified solution space by applying mutation operator;
7) Check of solution stagnancy.
Note that the first five steps are the same as the TS al-
gorithm, while Step 6 generates new solutions with hi-
gher degree of diversification in order to increase the
probability of finding the global optima, and Step 7
avoids spending too much computational efforts in order
to have a balance between the computational effective-
ness and efficiency.
For the CF solver, the insertion strategy is applied to
produce a new neighborhood solution and the values of
parameters are given below: tabu list size is equal to 7, a
limit of iterations for each run is set to 1000 and the mu-
tation probability for each gene is set at 0.8.
3.4 Database
A database server machine may be physically different
from the Web server that maintains the database. Due to
the MySQL is the world's most popular open source da-
tabase. Hence, we use MySQL server as the database-
server in this study. This remote database is accessed
Con struct initial solutio
n
Start
Improve neighborhood
solutions
U
p
da te ta bu l ist
Is it better
than best
solutions
found so far?
T
erm
i
nat
i
on
conditions
met?
Is ittiming
for
mutation?
Reset solution
st agna ncy cou nte r
and update best
solution s so far
Apply mutation
operator and
gene ra te ne w
solution
Reset mutation
counte
r
Repo rt best solutions
foundEnd
Yes
N
o
Yes
N
o
Yes
N
o
In itia lize thecont rolparameter s
Increasemutation
counter and stagnancy
cou nter
Figure 5. Flowchart of CF solver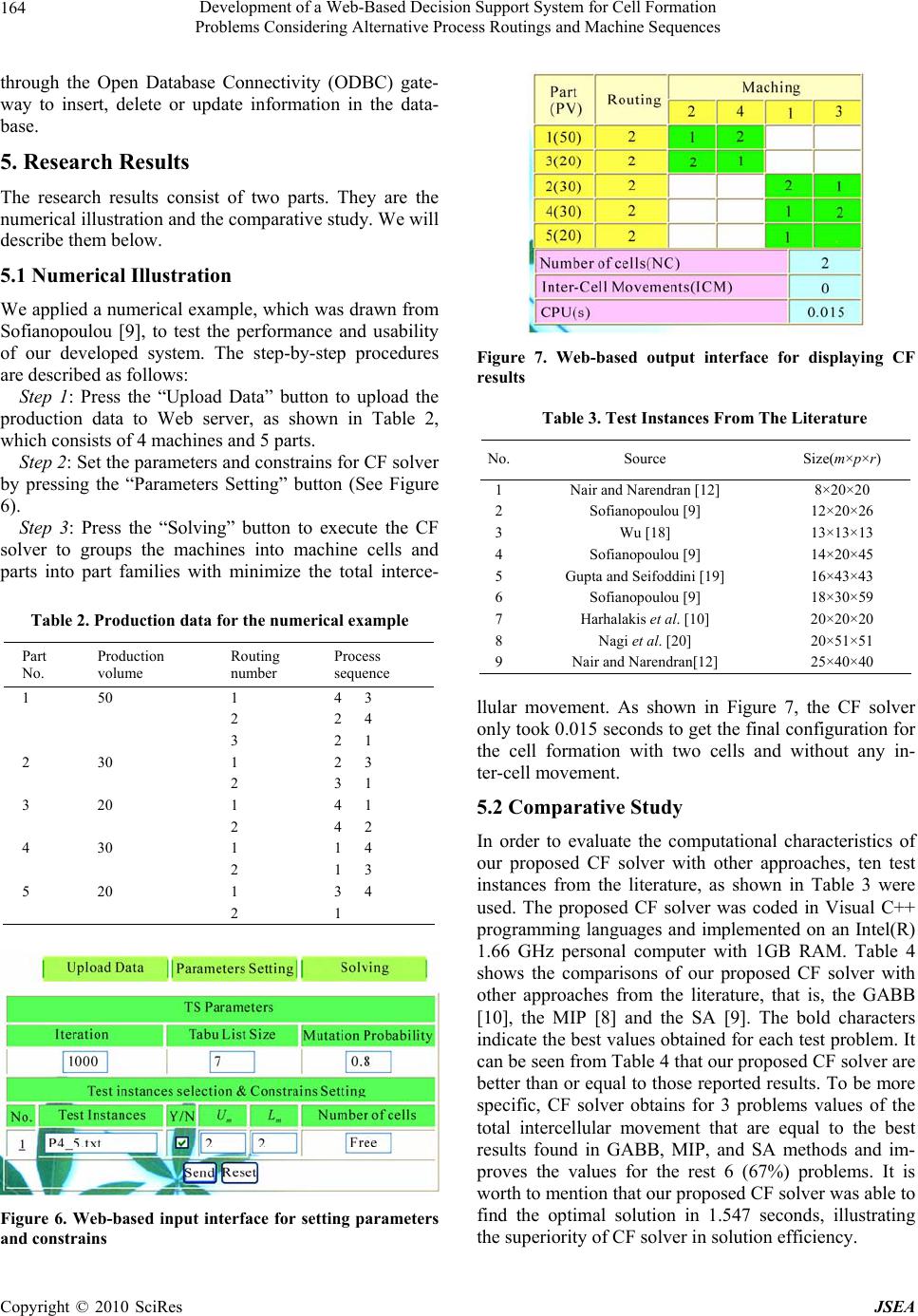

Development of a Web-Based Decision Support System for Cell Formation 164 Problems Considering Alternative Process Routings and Machine Sequences
through the Open Database Connectivity (ODBC) gate-
way to insert, delete or update information in the data-
base.
5. Research Results
The research results consist of two parts. They are the
numerical illustration and the comparative study. We will
describe them below.
5.1 Numerical Illustration
We applied a numerical example, which was drawn from
Sofianopoulou [9], to test the performance and usability
of our developed system. The step-by-step procedures
are described as follows:
Step 1: Press the “Upload Data” button to upload the
production data to Web server, as shown in Table 2,
which consists of 4 machines and 5 parts.
Step 2: Set the parameters and constrains for CF solver
by pressing the “Parameters Setting” button (See Figure
6).
Step 3: Press the “Solving” button to execute the CF
solver to groups the machines into machine cells and
parts into part families with minimize the total interce-
Table 2. Production data for the numerical example
Part
No. Production volume Routing number Process sequence
1 50 1 4 3
2 2 4
3 2 1
2 30 1 2 3
2 3 1
3 20 1 4 1
2 4 2
4 30 1 1 4
2 1 3
5 20 1 3 4
2 1
Figure 6. Web-based input interface for setting parameters
and constrains
Figure 7. Web-based output interface for displaying CF
results
Table 3. Test Instances From The Literature
No.Source Size(m×p×r)
1Nair and Narendran [ 12] 8×20×20
2Sofianopoulou [9] 12×20×26
3Wu [18] 13×13×13
4Sofianopoulou [9] 14×20×45
5Gupta and Seifoddini [19] 16×43×43
6Sofianopoulou [9] 18×30×59
7Harhalakis et al. [10] 20×20×20
8Nagi et al. [20] 20×51×51
9Nair and Narendran[12] 25×40×40
llular movement. As shown in Figure 7, the CF solver
only took 0.015 second s to get the final configuration for
the cell formation with two cells and without any in-
ter-cell movement.
5.2 Comparative Study
In order to evaluate the computational characteristics of
our proposed CF solver with other approaches, ten test
instances from the literature, as shown in Table 3 were
used. The proposed CF solver was coded in Visual C++
programming languages and implemented on an Intel(R)
1.66 GHz personal computer with 1GB RAM. Table 4
shows the comparisons of our proposed CF solver with
other approaches from the literature, that is, the GABB
[10], the MIP [8] and the SA [9]. The bold characters
indicate the best values obtained for each test problem. It
can be seen from Table 4 that our proposed CF solver are
better than or equal to those reported results. To be more
specific, CF solver obtains for 3 problems values of the
total intercellular movement that are equal to the best
results found in GABB, MIP, and SA methods and im-
proves the values for the rest 6 (67%) problems. It is
worth to mention that our prop osed CF solver was ab le to
find the optimal solution in 1.547 seconds, illustrating
the superiority of CF solver in solution efficien cy.

Development of a Web-Based Decision Support System for Cell Formation 165
Problems Considering Alternative Process Routings and Machine Sequences
Table 4. Performance of the proposed approach compared
to other approaches
Test instances Other approaches Proposed approach
GABB[
10] MIP[8] SA[9] CF solver
No. Lm U
m
ICM ICM ICM NC ICM CPU (s)
1 2 4 13 - - 2 13 0.273
2 2 5 - - 29 3 29 0.500
3 2 6 - 1800 - 3 12600.360
4 2 5 - - 25 3 25 0.578
5 2 6 - 34979 - 3 274160.907
6 2 7 - - 34 3 32 0.774
7 2 5 18 - - 5 17 0.953
8 2 5 86 - - 5 82 1.789
9 2 4 39 - - 7 33 1.547
6. Conclusions
Considering alternative process routings and machine
sequences to cell formation (CF) problems makes the
problems more realistic. New technologies, especially
the World-Wide Web (WWW) technologies, have cre-
ated many opportunities for research about Decision
Support Systems (DSS). In this study, a Web-based CF
DSS considering alternative process routings and ma-
chine sequences simultaneously has been proposed. With
the assistance of CF DSS, the CF practitioners in the
production departments can interact with the systems
without knowing the details of algorithms and can get the
best machine cells and part families with minimize the
total intercellular movement wherever and whenever
they may need it. An example taken from the literature
was adopted for illustrational purpose. To further verify
the feasibility and effectiv eness of the system developed,
a set of test problems with various sizes drawn from the
literature have be used to test the performance of the CF
solver. Corresponding results were compared to several
well-known algorithms previously published. The results
indicated that the proposed CF solver improved the best
results found in the literature for 67% of the test prob-
lems and the CPU times took by our proposed CF solver
to find the optimal solutio n were in 1.547 second s. These
show that our developed system should be very effective,
efficient and practical.
REFERENCES
[1] S. Heragu, “Facilities design,” Massachusetts: PWS
Publishing Company, Boston, 1997.
[2] U. Wemmerlov and N. Hyer, “Research issues in cellular
manufacturing,” International Journal of Production Re-
search, Vol. 25, pp. 413–431, 1987.
[3] A. Kusiak, “Intelligent manufacturing systems,” New
Jersey: Prentice Hall, Englewood Cliffs, 1990.
[4] Y. Yin and K. Yasuda, “Similarity coefficient methods
applied to the cell formation problem: A taxonomy and
review,” International Journal of Production Economics,
Vol. 101, pp. 329–352, 2006.
[5] A. Kusiak, “The generalized group technology concept,”
International Journal of Production Research, Vol. 25, pp.
561–569, 1987.
[6] M. S. J. Ameli and J. Arkat, “Cell formation with alterna-
tive process routings and machine reliability considera-
tion,” International Journal of Advanced Manufacturing
Technology, Vol. 35, pp. 761–768, 2008.
[7] F. Boctor, “A linear formulation of the machine-part cell
formation problem,” International Journal of Production
Research, Vol. 29, No. 2, pp. 343–356, 1991.
[8] Y. Y. Won and K. C. Lee, “Group technology cell forma-
tion considering operation sequences and production vol-
umes,” International Journal of Production Research, Vol.
39, No. 13, pp. 2755–2768, 2001.
[9] S. Sofianopoulou, “Manufacturing cells design with alter-
native process plans and/or replicate machines,” Interna-
tional Journal of Production Research, Vol. 37, pp. 707–
720, 1999.
[10] M. Boulif and K. Atif, “A new branch-&-bound-enhanced
genetic algorithm for the manufacturing cell formation
problem,” Computers and Operations Research, Vol. 33,
pp. 2219–2245, 2006.
[11] T.-H. Wu, S.-H. Chung, and C.-C. Chang, “Hybrid simu-
lated annealing algorithm with mutation operator to the
cell formation problem with alternative process routings,”
Expert Systems with Applications, Vol. 36, pp. 3652–
3661, 2008.
[12] G. J. Nair and T. T. Narendran, “CASE: A clustering
algorithm for cell formation with sequence data,” Interna-
tional Journal of Production Research, Vol. 36, pp. 157–
179, 1998.
[13] J. McAuley, “Machine grouping for efficient production,”
Production Engineer, Vol. 52, pp. 53–57, 1972.
[14] S. Lozano, B. Adenso-Diaz, and L. Onieva, “A one-step
Tabu search algorithm for manufacturing cell design,”
Journal of the Operational Research Society, Vol. 50, pp.
509–516, 1999.
[15] G. Y. Tian, G. Yin, and D. Taylor, “Internet-based manu-
facturing: A review and a new infrastructure for distrib-
uted intelligent manufacturing,” Journal of Intelligent
Manufacturing, Vol. 13, No. 5, pp. 323–338, 2002.
[16] J. Lee, “E-manufacturing systems: Fundamental and too-
ls,” Robotics and Computer-Integrated Manufacturing,
Vol. 9, No. 6, pp. 501–507, 2003.
[17] C. S. Smith and P. K. Wright, “CyberCut: A world-wide
web-based design-to-fabrication tool,” Journal of Intelli-
gent Manufacturing, Vol. 15, No. 6, pp. 432–442, 1996.
[18] N. Wu, “A concurrent approach to cell formation and
assignment of identical machines in group technology,”

Development of a Web-Based Decision Support System for Cell Formation
Problems Considering Alternative Process Routings and Machine Sequences
166
International Journal of Production Research, Vol. 36, pp.
2099–2114, 1998.
[19] T. Gupta and H. Seifoddini, “Production data based simi-
larity coefficient for machine-part grouping decisions in
the design of a cellular manufacturing system,” Interna-
tional Journal of Production Research, Vol. 28, pp. 1247–
1269, 1990.
[20] R. Nagi, G. Harlarakis, and J. M. Proth, “Multiple rout-
ings and capacity considerations in group technology ap-
plications,” International Journal of Production Research,
Vol. 28, pp. 2243–2257, 1990.