J. Biomedical Science and Engineering, 2010, 3, 193-199
doi:10.4236/jbise.2010.32025 Published Online February 2010 (http://www.SciRP.org/journal/jbise/
JBiSE
).
Published Online February 2010 in SciRes. http://www.scirp.org/journal/jbise
Classification of non stationary signals using multiscale
decomposition
Marwa Chendeb1,2, Mohamad Khalil2*, David Hewson1, Jacques Duchêne1
1ICD, FRE CNRS 2848, University of Technology of Troyes, Troyes, France;
2LaSTRe Laboratory, Engineering Section 1, Lebanese University, Tripoli, Lebanon.
Received 15 July 2008; revised 5 December 2009; accepted 11 December 2009.
ABSTRACT
The aim of this article is to develop an automatic al-
gorithm for the classification of non stationary sig-
nals. The application context is to classify uterine
electromyogram (EMG) events to prevent the onset
of preterm birth. The idea is to discriminate between
the events by allocating them to the physiological
classes: contractions, foetus motions, Alvarez or Long
Duration Low Frequency waves. Our method is
based on the Wavelet Packet (WP) decomposition
and the choice of a best basis for classification pur-
pose. Before classification, there is a need to detect
events in the recorded signals. The discrimination
criterion is based on the calculation of the ratio be-
tween intra-class variance and total variance (sum of
the intra-class and inter-class variances), calculated
directly from the coefficients of the selected WP. We
evaluated the performance of the algorithm on real
signals by using the classification methods Neural
Networks (NN) and Support Vector Machines (SVM).
Subband energies of the best selected WP are used as
effective features. The determined best basis is ap-
plicable to a wide range of uterine EMG signals from
large range of patients. In most cases, more than
85% of events are well classified whatever the term of
gestation.
Keywords:Uterine EMG; Preterm Birth; Wavelet Packet;
Best Basis; Event Classification
1. INTRODUCTION
The automatic classification of non stationary signals is
an important studied problem especially as the nonsta-
tionarity precludes classification in the time or frequency
domain [1]. The aim of this paper is to use the nonpara-
metric representation wavelet packet transform (WPT)
which is suitable for nonstationary signals and choose
among the wavelet packets (WPs) the best basis for clas-
sification. The application context is the classification of
uterine electromyographic (EMG) events used for the
prevention of preterm birth. The progress of labour can
be assessed non-invasively using EMG signals from the
uterus (the driving force for contractility) recorded from
the abdominal surface [2,3].
Preterm labour and resultant preterm birth are the
most important problems in perinatology [2,4,5].
Knowledge of labor commencement, as well as the pos-
sible prediction of its starting time, would be of great
interest in terms of limiting unnecessary stays in hospi-
tals and adapting treatment to the actual state of the
pregnancy. The principal events extracted from the rele-
vant activities of uterine EMG are the contractions (CT).
Other events can be of value for pre-term birth diagnosis:
Alvarez (Alv) waves, foetus motions (MAF) and
long-duration low-frequency (LDBF) waves [2] (Figure
1). Several works have been carried out on mammals,
with electrodes placed on the uterine surface [2,5]. They
demonstrated a modification in electrical activity during
both preterm and term labor. In [6] the uterine EMG
signals are classified using artificial neural networks
method to distinguish the normal term labour from ab-
normal preterm labour signals. [7] applied the wavelet
transform on the uterine signals recorded using abdomi-
nal surface electrodes. In literature, the best basis algo-
rithm is used to find the best-adapted WP for a lot of
goals such the detection [8,9], denoising [10], feature
extraction and classification [11,12], etc. Saito and
Coifman introduced the Local Discriminant Bases (LDB)
to search a best basis for classification [12]. Wavelet
packet analysis is used to extract the features of the
sample DNA sequences in [13]. An index of discrimina-
tion based on Kullback-Leibler distance is proposed as a
way to select most discriminant wavelet packets for tex-
ture classification in an image [14].
In this work, classification of uterine EMG events by
allocating them to the physiological classes: CT, MAF,
Alv, or LDBF waves.is based on their energy distribu-
tion throughout the wavelet packet transform (WPT)
which is used because it is characterized by the frequency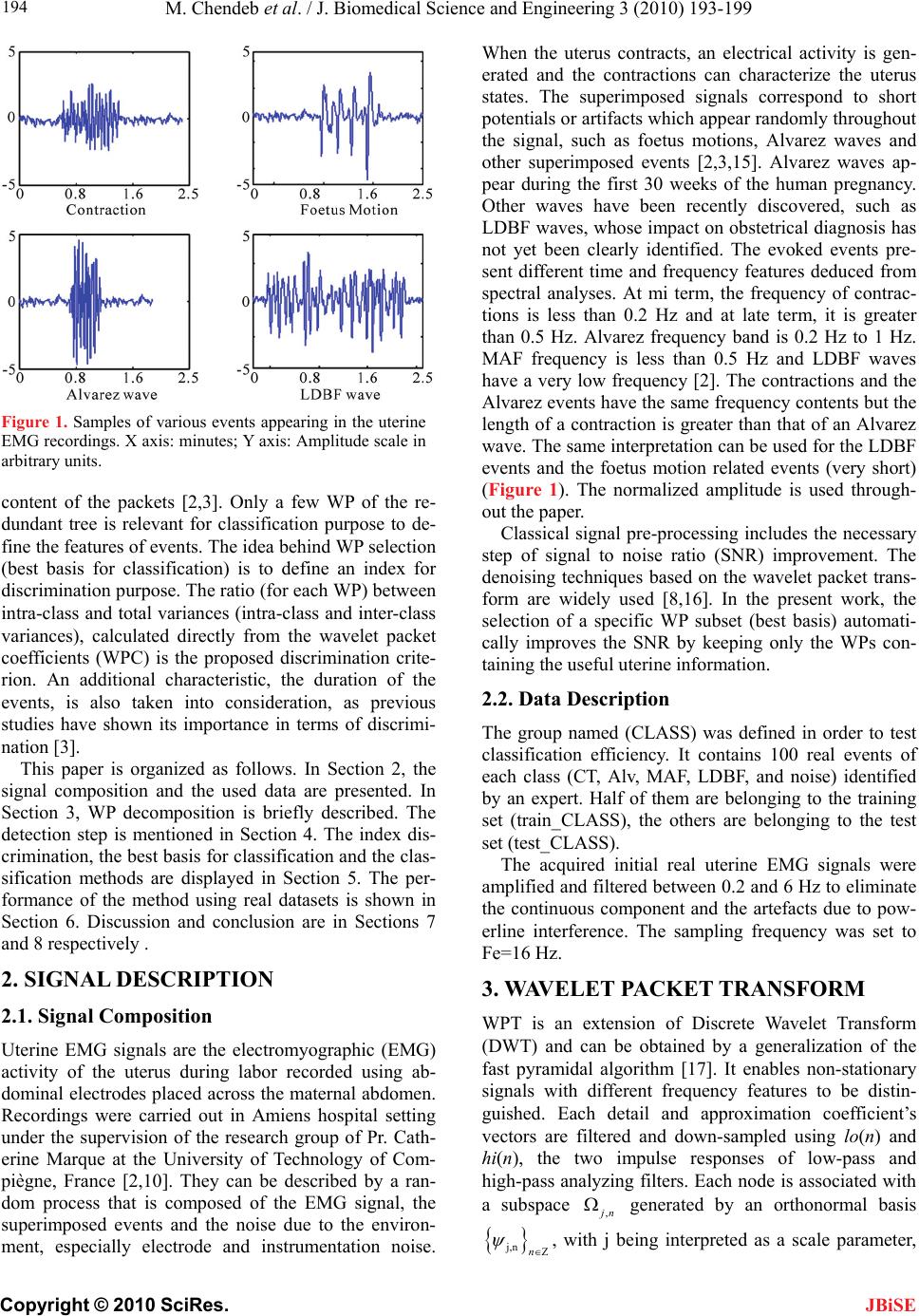

M. Chendeb et al. / J. Biomedical Science and Engineering 3 (2010) 193-199
194
JBiSE
Figure 1. Samples of various events appearing in the uterine
EMG recordings. X axis: minutes; Y axis: Amplitude scale in
arbitrary units.
content of the packets [2,3]. Only a few WP of the re-
dundant tree is relevant for classification purpose to de-
fine the features of events. The idea behind WP selection
(best basis for classification) is to define an index for
discrimination purpose. The ratio (for each WP) between
intra-class and total variances (intra-class and inter-class
variances), calculated directly from the wavelet packet
coefficients (WPC) is the proposed discrimination crite-
rion. An additional characteristic, the duration of the
events, is also taken into consideration, as previous
studies have shown its importance in terms of discrimi-
nation [3].
This paper is organized as follows. In Section 2, the
signal composition and the used data are presented. In
Section 3, WP decomposition is briefly described. The
detection step is mentioned in Section 4. The index dis-
crimination, the best basis for classification and the clas-
sification methods are displayed in Section 5. The per-
formance of the method using real datasets is shown in
Section 6. Discussion and conclusion are in Sections 7
and 8 respectively .
2. SIGNAL DESCRIPTION
2.1. Signal Composition
Uterine EMG signals are the electromyographic (EMG)
activity of the uterus during labor recorded using ab-
dominal electrodes placed across the maternal abdomen.
Recordings were carried out in Amiens hospital setting
under the supervision of the research group of Pr. Cath-
erine Marque at the University of Technology of Com-
piègne, France [2,10]. They can be described by a ran-
dom process that is composed of the EMG signal, the
superimposed events and the noise due to the environ-
ment, especially electrode and instrumentation noise.
When the uterus contracts, an electrical activity is gen-
erated and the contractions can characterize the uterus
states. The superimposed signals correspond to short
potentials or artifacts which appear randomly throughout
the signal, such as foetus motions, Alvarez waves and
other superimposed events [2,3,15]. Alvarez waves ap-
pear during the first 30 weeks of the human pregnancy.
Other waves have been recently discovered, such as
LDBF waves, whose impact on obstetrical diagnosis has
not yet been clearly identified. The evoked events pre-
sent different time and frequency features deduced from
spectral analyses. At mi term, the frequency of contrac-
tions is less than 0.2 Hz and at late term, it is greater
than 0.5 Hz. Alvarez frequency band is 0.2 Hz to 1 Hz.
MAF frequency is less than 0.5 Hz and LDBF waves
have a very low frequency [2]. The contractions and the
Alvarez events have the same frequency contents but the
length of a contraction is greater than that of an Alvarez
wave. The same interpretation can be used for the LDBF
events and the foetus motion related events (very short)
(Figure 1). The normalized amplitude is used through-
out the paper.
Classical signal pre-processing includes the necessary
step of signal to noise ratio (SNR) improvement. The
denoising techniques based on the wavelet packet trans-
form are widely used [8,16]. In the present work, the
selection of a specific WP subset (best basis) automati-
cally improves the SNR by keeping only the WPs con-
taining the useful uterine information.
2.2. Data Description
The group named (CLASS) was defined in order to test
classification efficiency. It contains 100 real events of
each class (CT, Alv, MAF, LDBF, and noise) identified
by an expert. Half of them are belonging to the training
set (train_CLASS), the others are belonging to the test
set (test_CLASS).
The acquired initial real uterine EMG signals were
amplified and filtered between 0.2 and 6 Hz to eliminate
the continuous component and the artefacts due to pow-
erline interference. The sampling frequency was set to
Fe=16 Hz.
3. WAVELET PACKET TRANSFORM
WPT is an extension of Discrete Wavelet Transform
(DWT) and can be obtained by a generalization of the
fast pyramidal algorithm [17]. It enables non-stationary
signals with different frequency features to be distin-
guished. Each detail and approximation coefficient’s
vectors are filtered and down-sampled using lo(n) and
hi(n), the two impulse responses of low-pass and
high-pass analyzing filters. Each node is associated with
a subspace ,
j
n

generated by an orthonormal basis


j,n n


, with j being interpreted as a scale parameter,

M. Chendeb et al. / J. Biomedical Science and Engineering 3 (2010) 193-199
195
JBiSE
and n as a sequence parameter. The wavelet packet coef-
ficients (WPC) at each node (j,n) are computed as [17]:
0
14

,,
()(),(2 )
j
jn jn
Ckftt k   (1) 1 2
13
where f(t) is the initial signal and k is the time-local-
ization index. In the following, each WP is characterized
by the sequential index v obtained by according sequen-
tial numbers to the WP (see Figure 2). In fact, WPC
carry the same information as the reconstructed signals.
As WPT is a linear transformation, WPC exhibit the
same statistical properties as the initial signal [8]. Con-
sequently, WPC of the real noise follow the normal dis-
tribution [15].
3 4
12
5 6
7 8
15
9
16
10
17
11
18 1920 21222324 25262728 2930
4. DETECTION
To detect events, several methods can be used. In our
last work [15] an algorithm of best basis for detection is
proposed. It is based on the Kullback Leibler distance as
a criterion to select the best WPs which show clearly the
events. After choosing the best basis, the detection algo-
rithm DCS (Dynamic Cumulative Sum) is applied on
every selected wavelet packet coefficients. After the de-
lay correction and the change time fusion [15], the uter-
ine events of the real signals are obtained.
5. CLASSIFICATION
After change detection, the problem consists in identify-
ing the detected events by allocating them to physio-
logical classes: contractions, foetus motions, Alvarez
waves, LDBF waves, or noise. In this section, the classi-
fication criterion is described. The approach of best basis
is proposed for the classification task. The principal fea-
tures for the classification methods are the variances of
the selected packets. The duration of events was intro-
duced as an additional feature to improve the correct
classification rate (CCR).
5.1. Classification Criterion
An important criterion to discriminate between classes is
to minimise the intra class variance and to maximise
inter-class variance. In [18] an index which maximises
the Euclidian distance between the classes was used. The
most discriminant coefficients of all packets were se-
lected as a criterion for classification [19]. In our work,
the ratio between intra-class variance and total variance
(sum of inter-class and intra-class variances) calculated
for each WP seems to be an efficient index for discrimi-
nation. As the uterine EMG events are characterised by
their frequency content, the variances of selected WPs
produce useful information to identify events.
For the level of decomposition J, the number N of
packets is:
1
2
J
N 
Figure 2. Wavelet packet decomposition tree.
Suppose that the ith class is composed of mi elements,
so the gravity center of this class is:
^
1
1i
vn
v
iq i
q
i
g
x
m


(3)
where v
iq
x
is the qth element of class i (i = 1.5) and WP
number v.
The gravity center global of WP v is:
^
1
1
vv
M
qq
q
^
g
mg
m
 (4)
where M is the number of classes (in our case M =5) and
m is the total number of samples.
The intra-class variance of a WP number v is de-
fined as:
^v
w 
2
^
^
11
1i
vm
M
vv
wiq i
iq
xg
m

 


 

(5)
where
^
v
i
g
is the center of gravity of the packet v and
class i, mi the number of elements of class i, M the total
number of classes and v
iq
x
is the qth element of the
packet v and class i.
The inter-class variance
^v
B
 of WP v is written as:
2
^
^^
1
1
vv
M
v
Bii
i
mg g
m

 



(6)
where gv is the centre of gravity for all classes.
The total variance
^

is equal to the sum of the in-
ter-class and intra-class variances [20]:
^^^
vv
w
v
B

  (7)
For each packet v, define the discrimination criterion as
follows:
^
^
v
w
v
v
R



(8)
1 (2)

M. Chendeb et al. / J. Biomedical Science and Engineering 3 (2010) 193-199
196
JBiSE
5.2. Best Basis Selection for Classification
The goal of this part is to retain only the wavelet packets
that are able to discriminate between events in a specific
class of signals (uterine EMG in our application). If the
distances between classes are important and each class is
strongly concentrated, the ratio Rv of packet v is small.
In this case, the classes are well separated and the packet
is one of the best WPs for classififcation.
The values of criterion Rv are calculated for all WP
and sorted in ascending order. There is a clear gap be-
tween the values of Rv corresponding to the packets that
are relevant for classification and the others (Figure 3),
a threshold can be indicated. As the tree is highly redun-
dant, there is a need for further step to reduce the num-
ber of selected packets based on the frequency contents
of events. In our case, the packets which contain the
bandwidths of the events are retained as best basis for
classification. The variances of the retained WPs (best
basis) are used as features for the classification methods.
5.3. Classification Methods
Classification has been achieved using the two methods:
neural networks (NN) [21] and Support Vector Machines
(SVM) [22,23].
5.3.1. Neural Networks
The Multi Layer Perceptron (MLP) is widely used to
solve classification problems using supervised training
for instance, the feed forward technique, which is used
to minimize error. A multilayer perceptron is a feedfor-
ward artificial neural network model that maps sets of
input data onto a set of appropriate output [24].
Such a network is based on the calculation of the out-
put (direct calculation, weights are fixed) and adjustment
of the weight by minimizing an error function. The
process continues until the outputs of the network
Figure 3. Rv values of each WP plotted in ascending order.
X axis: arbitrary units. Y axis: Rv values.
be come close to those desired. The network is defined
by the transfer function of the neuron, the number of
layers and the number of neurons in each layer. The
number of inputs is equal to the dimension of the input
vectors (in this case the variances of the selected pack-
ets). The number of outputs depends on the number of
classes. Various transfer functions (sigmoid, hyperbolic
tangent, linear, etc) can be used as neural activation
functions [24].
5.3.2. Support Vector Machines
The SVM method is a new discriminator based on the
construction of an optimal hyperplane, which is con-
structed in such a way that it maximizes the minimal
distance between itself and the learning set.
Support vector machine is a learning technique which
is well-founded in modern statistical learning theory [22].
It uses the training data to create the optimal separating
hyperplane between two classes. The optimal hyperplane
maximizes the margin of the closest data points. In this
way the SVM minimizes the misclassification probabil-
ity of new cases. The optimal separating hyperplane is
computed as a decision surface of the form:
1
(y)sgn(y ,y)
s
l
ii i
i
g
dK b 






 (9)
where xi are support vectors which are determined from
the training data, is the inner product kernel
which must satisfy Mercer’s theorem [22], and is used to
map the data from its original dimension to higher di-
mension so that the data is linearly separable in the
mapped dimension, ls is the number of support vectors,
di is the class indicator
(y ,y)
i
K



1, 1
i
d
i
of xi, and b is
bias. The coefficients

are calculated by solving the
quadratic programming problem:
Maximize

1,1
1,
2
ll
iijiji
iij
ddK yy 




j
l
(10)
Subject to
1
0, 01,...,
l
ii i
i
dCfori 

 

where C is a user specified positive regularization pa-
rameter used to control he amount of allowed overlap
between classes. Given the expression of g(y), the deci-
sion is based on the sign of g(y). In this work a radial
basis function (RBF) is chosen as inner product kernel,
which is defined as:
2
2
( ,)exp()
2
uv
Kuv


 (11)
where 0

 is a user specified constant which defines
the kernel width. In RBF kernel support vector machine,
number and value properties of support vectors deter-

M. Chendeb et al. / J. Biomedical Science and Engineering 3 (2010) 193-199
197
mine the number of kernels and their centers [8]. Using
RBF as an inner product kernel provides classification of
a non-linear set of data, which means perfect discrimina-
tion of the prostate texture features.
JBiSE
To discriminate between the various uterine events,
the SVM multiclass method [23] was used. It is based on
building a model SVM for each group of events, ena-
bling discrimination in comparison to the other groups.
6. RESULTS ON CLASSIFICATION
As the main discriminant feature of the events contained
in uterine EMG recordings is the frequency content, the
decomposition was performed up to level 4. The used
wavelet is symlet 5 [15]. For this, every event was de-
composed onto 30 WP (Figure 2). This choice is justi-
fied by the fact that the level 4 is the limit where WP still
contain relevant information related to all the uterine
events. For example, the WPs 15 and 16 correspond to
the frequency bands which belong MAF and LDBF
waves.
In detection case, the decomposition level is limited to
3 because the goal was to choose the best packets for
detection whatever the events [15]. To decide which
packets were able to classify the events, the values Rv of
the discrimination criterion were computed on each
packet using equation 8 (there are 30 packets). The
events of train_CLASS were used (see Subsection 2.2).
Figure 3 shows the criterion values in ascending order.
The selection of the discriminant WP was made by ap-
plying a threshold and selecting those WP which have
the smallest criterion values.
By examining Figure 3 there is a clear threshold for
Rv. In first step, the packets 1, 3, 7, 15 and 16 were se-
lected. These packets correspond to the bandwidths [0,
4], [0, 2], [0, 1], [0, 0.05] and [0.05, 1] Hz, respectively.
The second step consists in eliminating the redundant
packets by keeping only the packets which correspond to
the frequency contents of events. As the contractions and
Alvarez waves have a frequency band less than 1 Hz,
MAF frequency is less than 0.5 Hz and LDBF waves
have a very low frequency (see Subsection 2.1), only the
packets 7, 15 and 16 are retained as best basis for classi-
fication.
In order to demonstrate that Rv is a good criterion to
discriminate between uterine classes, the validation step
is carried out. The classification methods MLP and SVM
were applied on the test_CLASS to evaluate the Correct
Classification Rate (CCR).
In the current application, a two layer feed forward
network is created. The first layer has five tansig
2
2
() 1
1n
fn e







neurons, the second layer has ten pure-
lin (f(n) = n) neurons.
For the SVM method, the CCR were calculated for
some kernels (linear, polynomial, sigmoid and Gaussian
Radial Basis Function (GRBF)) [22]. The kernel GRBF
gave the best CCR, it is defined as follows [22]:
2
2
( ,)exp()
2
uv
Kuv


 (12)
To provide the reader with the performance improve-
ment of the best basis with respect to the DWT, we also
present the CCR produced by using the packets 2, 4, 8
and 16 corresponding to the DWT. The variances of
packets 2, 4, 8 and 16 were used as features for the clas-
sification methods. The best basis method was evaluated
by comparing the results with those obtained using the
DWT. Results are summarized in Tables 1,2, showing
the performance of the use of the variances of the se-
lected WP as features for the classification methods.
Table 1 shows the CCR of MLP classifier for the best
basis selection and DWT. The CCR were calculated for
large values of the regularization parameter C and σ for
the SVM method [22,23] (C = [0.0001, 0.001, 0.01, 0.1,
1, 10, 100, 1000, 10000, Infinity] and σ = [0.1, 0.2, 0.4,
0.6, 1, 5, 10]). C controls the tradeoff between the com-
plexity of the machine and the number of non- separable
points. C and σ are chosen for each class in such a way
that the best correct classification rates are obtained. The
optimal values of C and σ are presented in Table 2 for
the best basis selection and DWT.
Event duration is used as an additional feature to im-
prove the correct classification rate. The correct classifi-
cation and false alarm rates are presented in Table 3
after including the event durations in the case of best
basis. The results are well improved specifically for Al-
varez and MAF waves.
7. DISCUSSION
This paper developed a best basis selected from the
set of WP tree for classification. The uterine EMG
events are characterized by their frequency content jus-
tify the use of WPT. WP tree reduction is generally
guided by a certain criterion (depending on the WPT
objectives) based on the knowledge of a data (often sta-
tistical) model or the availability of training data. The
mother wavelet choice in the current work was based on
the minimum delay induced by applying detection algo-
rithms directly on the wavelet packet coefficients. The
choice was made using all available EMG events, lead-
ing to the selection of the Symlet 5 wavelet [15]. This
choice is probably due to the symmetrical shape of the
associated filters. It is better to study the influence of
Table 1. Correct classification rates in the cases of best basis
(WP: 7, 15 and 16) and DWT (WP: 2, 4, 8 and 16) for MLP
method.
SVM CT ALV MAF LDBF Noise
best basis0.80 0.80 0.86 0.88 0.94
DWT 0.52 0.62 0.62 0.66 0.94

M. Chendeb et al. / J. Biomedical Science and Engineering 3 (2010) 193-199
198
JBiSE
Table 2. Correct classification rates in the cases of best basis (WP: 7, 15 and 16) and DWT (WP: 2, 4, 8 and 16)
for SVM method.
SVM CT ALV MAF LDBF Noise
best basis 0.82
σ =5, C=Inf
0.64
σ =10, C=Inf
0.8
σ =5, C=Inf
0.88
σ =1, C=Inf
0.82
σ =5, C=100
DWT 0.54
σ =1, C=10
0.50
σ =0.2, C=Inf
0.60
σ =0.2, C=Inf
0.50
σ =0.4, C=10000
0.90
σ =0.6, C=1000
Table 3. Correct classification probabilities (a) and false alarm rates (b) for the two methods after including
event duration (best basis case).
CT ALV MAF LDBF Noise
Method (a) (b) (a) (b) (a) (b) (a) (b) (a) (b)
MLP 0.86 0.04 0.96 0.11 0.98 0 1.00 0.12 0.86 0.04
0.88 0.04 0.86 0.12 0.96 0 0.98 0.03 0.90 0.18
SVM σ =5, C=Inf

=5, C=1

=5, C=1

=10, C=1

=0.6, C=1
other wavelets to choose the best wavelet for classifica-
tion.
The best basis was searched for classification. Four
levels were needed as they corresponded to the relevant
bandwidths for event discrimination such as foetus mo-
tions and LDBF waves.
The ratio between intra-class and inter-class variances
appeared as a good discrimination criterion for the
choice of the best basis for the classification of uterine
EMG events. The best basis for classification was se-
lected by choosing all packets that scored a ratio lower
than a defined threshold as explained in Section 4. A
second step based on the frequency contents of events is
introduced to eliminate the redundant packets. In order
to ensure the performance of the selection of best basis,
we asked an expert in uterine EMG events to indicate,
from an arbitrary data set, which WP could discriminate
between the uterine events at best. She selected the same
WP obtained by our algorithm.
This result illustrates the coincidence between the
automatic unsupervised learning and direct supervised
selection. Two classification methods (Neural Networks
(MLP) and Support Vector Machines) were applied on
validation and test data. The main issues related to the
use of MLP were the choice of the activation functions
of the hidden and output layers and the definition of the
number of hidden neurons. Results were satisfactory
with or without the use of the event duration as a com-
plementary feature.
For SVM method, the parameter (C and σ) values that
produced the best CCR were selected. These values were
different according to whether the duration of the events
was used or not. The CCR were greatly improved by the
introduction of the event duration, whatever the classifi-
cation method.
8. CONCLUSIONS
The method proposed for event classification in uterine
recordings based on a WPT, and best basis selection in
order to reduce the WP tree produced very satisfactory
results. The ratio between intra-class and total variance
was found to be a good criterion well adapted for the
choice of the best discriminant packets. Two proposed
classifiers (Neural Networks and SVM) for the identifi-
cation of the detected events by allocating them to
physiological classes (CT, MAF, Alv or LDBF waves)
were used. On average more than 85% of the events
were correctly classified, regardless of the pregnancy
term. The training data permits to choose the best basis
relevant to the uterine EMG events but the algorithm can
be used for other similar situations. As perspectives the
study must continue in order to show the performance of
the algorithm when applying it to other non stationary
data.
Uterine electrical activity is increasingly used as a
relevant index for the characterization of the uterine con-
traction within the scope of pregnancy and parturition
monitoring. A further step would be the production of a
sufficiently large database to improve the current know-
ledge on the actual recording contents and their correla-
tion to a diagnosis of possible premature birth.
REFERENCES
[1] Gretton, A. et al. (2001) Nonstationary signal classifica-
tion using support vector machines. 11th IEEE Workshop
on Statistical Signal Processing Proceedings, pp.
305–308.
[2] Devedeux, D., Marque, C., Mansour, S., Germain, G.,
Duchene, J. (1993) Uterine electromyography: a critical
review. Amer. J. Obstet. Gynecol. 169(6), 1636–1653.
[3] Khalil, M., Duchene, J. (2000) Uterine EMG analysis: a
dynamic approach for change detection and classification.
IEEE Trans. Biomed. Eng, 47(6), 748–756.
[4] Garfield, R.E., Saade, G., Buhimschi, C., Buhimschi, I. et
al. (1998) Control and assessment of the uterus and cer-
vix during pregnancy and labour. European Society of

M. Chendeb et al. / J. Biomedical Science and Engineering 3 (2010) 193-199
199
JBiSE
Human and Embryology, 4(5), 673–695.
[5] Doret, M., Bukowski, R., Longo, M., Maul, H., Maner,
W.L., Garfield, R.E. and Saade, G.R. (2005) Uterine
electromyography characteristics for early diagnosis of
mifepristone-induced preterm labor. Obstetrics and Gy-
necology, 15(4), 822–830.
[6] Lu, N., Wang, J., McDermott, I., Thornton, S. et al. (2009)
Uterine electromyography signal feature extraction and
classification. International Journal of Modelling, Identi-
fication and Control, 6(2), 136–146.
[7] Eswaran, H., Wilson, J.D., Murphy, P., Preissl, H., Low-
ery C.L. (2002) The Journal of Maternal-Fetal & Neo-
natal Medicine, 11(3), 158–166.
[8] Ravier, P. and Amblard, P.O. (2001) Wavelet packets and
de- noising based on higher-order-statistics for transient
detection. Signal Processing, 81(9), 1909–1926.
[9] Hitti, E. and Lucas, M.F. (1998) Wavelet-packet basis
selection for abrupt changes detection in multicomponent
signals. Proc. EUSIPCO, Island of Rhodes, Greece,
1841–1844.
[10] Leman, H. and Marque, C. (2000) Rejection of the ma-
ternal electrocardiogram in the electrohysterogram signal,
IEEE Trans Biomed Eng. 47(8), 1010–1017.
[11] Yang, B., Yan, G., Yan, R., Wu, T. (2007) Adaptive sub-
ject-based feature extraction in brain–computer interfaces
using wavelet packet best basis decomposition. Medical
Engineering & Physics, 29(1), 48–53.
[12] Saito, N. and Coifman, R.R. (1994) Local discriminant
bases. A. F. Laine and M. A. Unser Editors, Wavelet Ap-
plications in Signal and Image Processing {II}, Proc.
SPIE 2303, 2–14.
[13] Zhao, J., Yang, X.W., Li, J.P. and Tang, Y.Y. (2001) DNA
sequences classification based on wavelet packet analysis
from “wavelet analysis and its applications book”.
Springer Berlin / Heidelberg editor.
[14] Rajpoot, N.M. (2002) Texture classification using dis-
criminant wavelet packet subbands. 45th Midwest Sym-
posium on Circuits and Systems, 3, 300–303.
[15] Chendeb, M., Khalil, M. and Duchêne J. (2006) Method-
ology of wavelet packet selection for event detection.
Signal Processing, 86, 3826–3841.
[16] Nadernejad, E. (2008) μPET data de-noising using
wavelet packets. Contemporary Engineering Sciences,
1(2), 91–104.
[17] Mallat, S. (1999) a wavelet tour of signal processing,
Academic Press, San Diego, CA.
[18] Sheng, S., Yanda, L. (1997) “Best Bases for Classifica-
tion”. Technical Report of pattern Recognition and Sig-
nal Processing Lab, department of Automation, Tsinghua
University.
[19] Fukunaga, K. (1990) “Introduction to statistical pattern
recognition”. Academic Press, Inc.
[20] Dubuisson, B. (1990) “Diagnostic et reconnaissance des
formes”. Editions Hermes.
[21] Turkoglu, I., Arslan, A. and Ilkay, E. (2003) An intelli-
gent system for diagnosis of the heart valve diseases with
wavelet packet neural networks. Computers in Biology
and Medicine, 33(4), 319–331.
[22] Gunn, S.R. (1998) Support vector machines for classifi-
cation and regression. Technical Report, School of Elec-
tronics and Computer Science, University of Southamp-
ton.
[23] Mayoraz, E. and Alpaydin, E. (1998) Support vector
machines for multi-class classification. Technical Report
IDIAP.
[24] Haykin, S.S., Gwynn, R. (2008) Neural networks and
learning machines. Prentice Hall, 3rd edition.