J. Biomedical Science and Engineering, 2010, 3, 160-166
doi:10.4236/jbise.2010.32021 Published Online February 2010 (http://www.SciRP.org/journal/jbise/
JBiSE
).
Published Online February 2010 in SciRes. http://www.scirp.org/journal/jbise
Study on synchrony of two uncoupled neurons under the
neuron’s membrane potential stimulation
Yue-Ping Peng1,2, Jue Wang1, Quan-Xing Miao2, Hong-Yan Lu2
1Key Laboratory of Biomedical Information Engineering of Education Ministry, Xi’an Jiaotong University, Xi’an, China;
2Communication Department, Engineering College of Armed Police Force, Xi’an, China.
Received 27 June 2009; revised 5 December 2009; accepted 7 December 2009.
ABSTRACT
The input current of two uncoupled Hindmarsh-Rose
neurons under different initial conditions is modu-
lated by the membrane potential of the Hindmarsh-
Rose neuron; and the synchronization characteristics
of the two uncoupled neurons are discussed by ana-
lyzing their membrane potentials and their inter
spike interval (ISI) distribution. Under the stimula-
tion of the neuron’s membrane potential whose dis-
charge pattern is period or the chaos, the two uncou-
pled neurons under different initial conditions, whose
parameter r (the parameter r is related to the mem-
brane penetration of calcium ion, and reflects the
changing speed of the slow adaptation current) is
different or the same, can realize the full synchroni-
zation (state synchronization) or discharge synchro-
nization (phase synchronization), and can only be
synchronized to the discharge pattern of the stimula-
tion neuron. The synchronization characteristics are
mainly related to the discharge pattern and the
strength of the stimulation neuron’s membrane po-
tential, and are little related to the parameter r and
the initial state of the two uncoupled neurons. This
investigation shows the characteristics of the neu-
ron’s membrane potential affecting the synchroniza-
tion process of neurons, and the neurons’ discharge
patterns and synchronization process can be adjusted
and controlled by the discharge pattern and the
strength of the stimulation neuron’s membrane po-
tential. This result is helpful to study synchronization
and encode of many neurons or neural network.
Keywords: The Membrane Potential; The HR Neuron;
Synchronization; ISI
1. INTRODUCTION
Since system synchronization was presented by Pecora,
et al. [1,2] in 1991, synchronization research has been
causing researchers’ wide focus in neuroscience field.
Nervous activities’ synchronization is found not only
among coupled neuron groups in the same brain region,
but also among uncoupled neuron groups in the same
brain region or among different cortical areas; Moreover,
it can cross over two semispheres of the brain [3]. So in
the nervous system, synchronization activities are pre-
sented not only among the coupled neurons, but also
among the uncoupled neurons. Studies on neuron syn-
chronization are mainly focused on two cases: the cou-
pled neurons and the uncoupled neurons; and the syn-
chronization of coupled neurons are studied more.
The Hindmarsh-Rose neuron (HR neuron) has several
characteristics of the excitable cell’s physical model and
many time scale discharge action [4,5,6,13]. There are
some literatures of studies on synchronization of HR
neurons [3,7,9,10,12,14,15,16,17]. Huerta, R. and Rabi-
novich, M.I. studied the period rhythm’s change of two
HR neurons coupled by the circuit and the synapse [7].
Two uncoupled HR neurons can be realized synchroni-
zation by applying input signals to modulate the neuron
model’s parameter or by applying the noise and the HR
neuron’s membrane potential to stimulate these neurons
[8,9,10]. The phase synchronization of two coupled HR
neurons was discussed by Shuai, JianWei and Durand,
D.M., and they concluded that the phase synchronization
is the discharge synchronization, the frequency synchro-
nization is the cluster synchronization, and the full syn-
chronization is the state synchronization [11]. Synchrony
of two uncoupled neurons under half wave sine current
stimulation was discussed, and it was concluded that the
two uncoupled HR neurons under different initial condi-
tions, whose parameter r is different or the same, can
realize discharge synchronization (phase synchronization)
or the full synchronization (state synchronization) [12].
In this study, we take two uncoupled HR neurons as
the object, and make the HR neurons different initial
discharge patterns by setting the value of the parameter r,
and apply the membrane potential of the Hindmarsh- This work is supported by the National Natural Science Foundation of
China (No. 30670660).

Y. P. Peng et al. / J. Biomedical Science and Engineering 3 (2010) 160-166
161
JBiSE
Rose neuron to modulate the two uncoupled HR neu-
rons’ input current, and discuss the HR neurons’ syn-
chronization characteristics by calculating and analyzing
the two neurons’ membrane potentials and their inter
spike intervals (ISIs).
2. THE DISCHARGE PATTERNS OF THE
HR NEURON MODEL
The HR neuron has many time scale dynamics action,
and its equation is set of three dimension ordinary dif-
ferential equations [4,5,6]:
32
x
yax bxzI 
2
ycdx y 
[() ]zrsxX z (1)
The HR neuron has three time variables: the mem-
brane potential variable x which has the quick depolari-
zation ability, the quick recovery variable y and slow
adaptation current variable z. I is the input stimulation
current; a, b, c, d, s, r and X are parameters. The pa-
rameter r is related to the membrane penetration of cal-
cium ion, and reflects the changing speed of the slow
adaptation current variable z. Other parameters have no
specific physical meaning. The equations are nondimen-
sional, and at numerical calculation, value of parameters
is as follows: a=1.0, b=3.0, c=1.0, d=5.0, s=4.0, I=3.0,
X=−1.56, and you can set the neuron at different dis-
charge patterns by changing the parameter r.
The discharge threshold value is −0.25, and if the
membrane potential is more than −0.25, the neuron will
produce one discharge process. Figure 1 is the ISI bi-
furcation figure of the neuron, where parameters except
r are set to the above values, and the initial state of the
neuron is (1.0, 0.2, 0.2). From Figure 1, the discharge
pattern of the neuron begins from the chaos state(r is
Figure 1. Bifurcation figure of the HR neuron under the
parameter r changing from 0.008 to 0.022.
Table 1. The values of the two neurons’ parameter r.
Case The values of r1 and r2
The same r1=r2=0.009, r1=r2=0.011,
r1=r2=0.013, r1=r2=0.0171, r1=r2=0.02
A little different
r1=0.0085 and r2=0.009,
r1=0.011 and r2=0.0115,
r1=0.014 and r2=0.0141,
r1=0.017 and r2=0.0171,
r1=0.021 and r2=0.0215
Much different
r1=0.0082 and r2=0.0115,
r1=0.014 and r2=0.0085,
r1=0.0085 and r2=0.017,
r1=0.009 and r2=0.021,
r1=0.011 and r2=0.0145,
r1=0.0112 and r2=0.017,
r1=0.0115 and r2=0.021,
r1=0.014 and r2=0.017,
r1=0.022 and r2=0.013,
r1=0.017 and r2=0.021
about 0.008~0.009), and evolves period 6 discharge pat-
tern(r is near 0.01), and via the adverse period doubling
bifurcation passes period 3(r is about 0.0105~0.012) and
enters the chaos state(r is about 0.0125~0.015) again,
and at last via the adverse period doubling bifurcation
passes period 4(r is about 0.016~0.018) and comes into
period 2(r is about 0.0185 ~0.022).
3. THE SYNCHRONIZATION OF TWO
UNCOUPLED HR NEURONS UNDER
THE STIMULATION OF THE
NEURON’S MEMBRANE
POTENTIAL
The equation set of two uncoupled HR neurons’ model is:
.32 ((
iiiiiiiiS
))
x
yax bxzIIt 
.2
iiii
ycdx y
i


.
[() ] iii iii zrsxX z

 (i=1, 2) (2)
Time variables of these two neurons are respectively
(x1, y1, z1) and (x2, y2, z2), and the parameters of these
two neurons are respectively (a1, b1, c1, d1, r1, s1, I1, X1)
and (a2, b2, c2, d2, r2, s2, I2, X2).
The equations are also nondimensional. At numerical
calculation, the values of these two neurons’ parameters
(except r) are as follows: a1=a2=1.0, b1=b2 =3.0,
c1=c2=1.0, d1=d2=5.0, s1=s2=4.0, X1=X2=−1.56, I1=I2=3.0;
and the values of the initial states of these two neurons
are respectively (1.0, 0.2, 0.2) and (−1.0, 0.8, 0.3); and
you can set these two neurons at different discharge pat-
terns by controlling values of the parameter ri (i=1, 2).
According to the difference of these two neurons’ pa-
rameter r, there are three cases: the parameter r is the
same, a little different (120.0005rr ), and much

Y. P. Peng et al. / J. Biomedical Science and Engineering 3 (2010) 160-166
162
JBiSE
different (120.003rr ). Table 1 shows the values of
the two neurons’ parameter r, and the discharge patterns
of these two neurons are correspondingly showed in the
Figure 1.
The value of the initial state of the stimulation neuron
is (0.2, 1, −0.2). The values of the parameters except r of
the stimulation neuron are as follows: a=1.0, b=3.0,
c=1.0, d=5.0, s=4.0, I=3.0, X=−1.56. The stimulation
neuron can be made different discharge patterns by
changing the parameter r according to Figure 1.
Total stimulation current includes two parts: the bias
current (I1 and I2) and the input stimulation current IS(t):
. x(t) is the membrane potential of the
stimulation neuron, and k is the stimulation strength of
the membrane potential. The stimulation neuron begins
to stimulate the system model after the bias current (I1
and I2) has been working for 500. The simulation time of
the system model is often 0~4000.
)()(tkxtI S
3.1. Synchronization under the Stimulation of
the Period Discharge Pattern
The values of the parameters of these two uncoupled
neurons are above given values. The parameter r of the
stimulation neuron is respectively 0.011, 0.017, and 0.02,
and its discharge pattern is respectively period 3, period
4, and period 2. Under each discharge pattern, the stimu-
lation strength k is respectively 0.5, 1, 2, 3, 6, 9, and 12.
The parameter r of the stimulation neuron is 0.011
(the discharge pattern is period 3). As it begins to stimu-
late the two neurons, in above all cases, the two uncou-
ple neurons’ discharge patterns totally change into dy-
namic period discharge pattern from the initial discharge
patterns with the stimulation strength k increasing, and
the changing trend of their membrane potentials’ ISI is
the same, namely gradually evolves into period 3 dis-
charge pattern which is the same as the stimulation neu-
ron’s. When the stimulation strength is 0.5 and 1, these
two neurons don’t realize synchronization, and when the
stimulation strength is 3, 6, 9 and 12, these two neurons
realize discharge synchronization (phase synchronization)
or the full synchronization (state synchronization) [11].
When the stimulation strength is 2, only several groups
of these two neurons realize discharge synchronization
or the full synchronization. When the parameter r is the
same, these two neurons realize the full synchronization.
When the parameter r is a little different, these two neu-
rons realize the full synchronization or discharge syn-
chronization. When the parameter r is much different,
these two neurons realize discharge synchronization or
the approximate full synchronization. The synchroniza-
tion discharge pattern is the same as the stimulation neu-
ron’s discharge pattern (period 3).
The parameter r of the stimulation neuron is 0.017
(the discharge pattern is period 4). As it begins to stimu-
late the two neurons, in above all cases, the two uncou-
ple neurons’ discharge patterns totally change into dy-
namic period discharge pattern from the initial discharge
patterns with the stimulation strength k increasing, and
the changing trend of their membrane potentials’ ISI is
the same, namely gradually evolves into period 4 dis-
charge pattern which is the same as the stimulation neu-
ron’s. When the stimulation strength is 0.5 and 1, these
two neurons don’t realize synchronization, and when the
stimulation strength is 3, 6, 9 and 12, these two neurons
realize discharge synchronization or the full synchroni-
zation. When the stimulation strength is 2, only several
groups of these two neurons realize discharge synchro-
nization or the full synchronization. When the parameter
r is the same, these two neurons realize the full synchro-
nization. When the parameter r is a little different, these
two neurons realize the full synchronization or discharge
synchronization. When the parameter r is much different,
these two neurons realize discharge synchronization or
the approximate full synchronization. The synchroniza-
tion discharge pattern is the same as the stimulation
neuron’s discharge pattern (period 4).
The parameter r of the stimulation neuron is 0.02 (the
discharge pattern is period 2). As it begins to stimulate
the two neurons, in above all cases, the two uncouple
neurons’ discharge patterns totally change into dynamic
period discharge pattern from the initial discharge pat-
terns with the stimulation strength k increasing, and the
changing trend of their membrane potentials’ ISI is the
same, namely gradually evolves into period 2 discharge
pattern which is the same as the stimulation neuron’s.
When the stimulation strength is 0.5 and 1, these two
neurons don’t realize synchronization, and when the
stimulation strength is 6, 9 and 12, these two neurons
realize discharge synchronization or the full synchroni-
zation. When the stimulation strength is 2 or 3, only sev-
eral groups of these two neurons realize discharge syn-
chronization or the full synchronization. When the pa-
rameter r is the same, these two neurons realize the full
synchronization. When the parameter r is a little differ-
ent, these two neurons realize the full synchronization or
discharge synchronization. When the parameter r is
much different, these two neurons realize discharge syn-
chronization or the approximate full synchronization.
The synchronization discharge pattern is the same as the
stimulation neuron’s discharge pattern (period 2).
Limited to the length, Figure 2 only shows the syn-
chronization process of the two neurons, where the pa-
rameter r of the stimulation neuron is 0.02, and the
stimulation strength k is 9. In Figure 2, from (a) and (d),
(b) and (e), (c) and (f), these two neurons respectively
realize the full synchronization, the full synchronization,
and the discharge synchronization; and the synchroniza-
tion discharge pattern is all period 2, which is the same
as the stimulation neuron’s discharge pattern.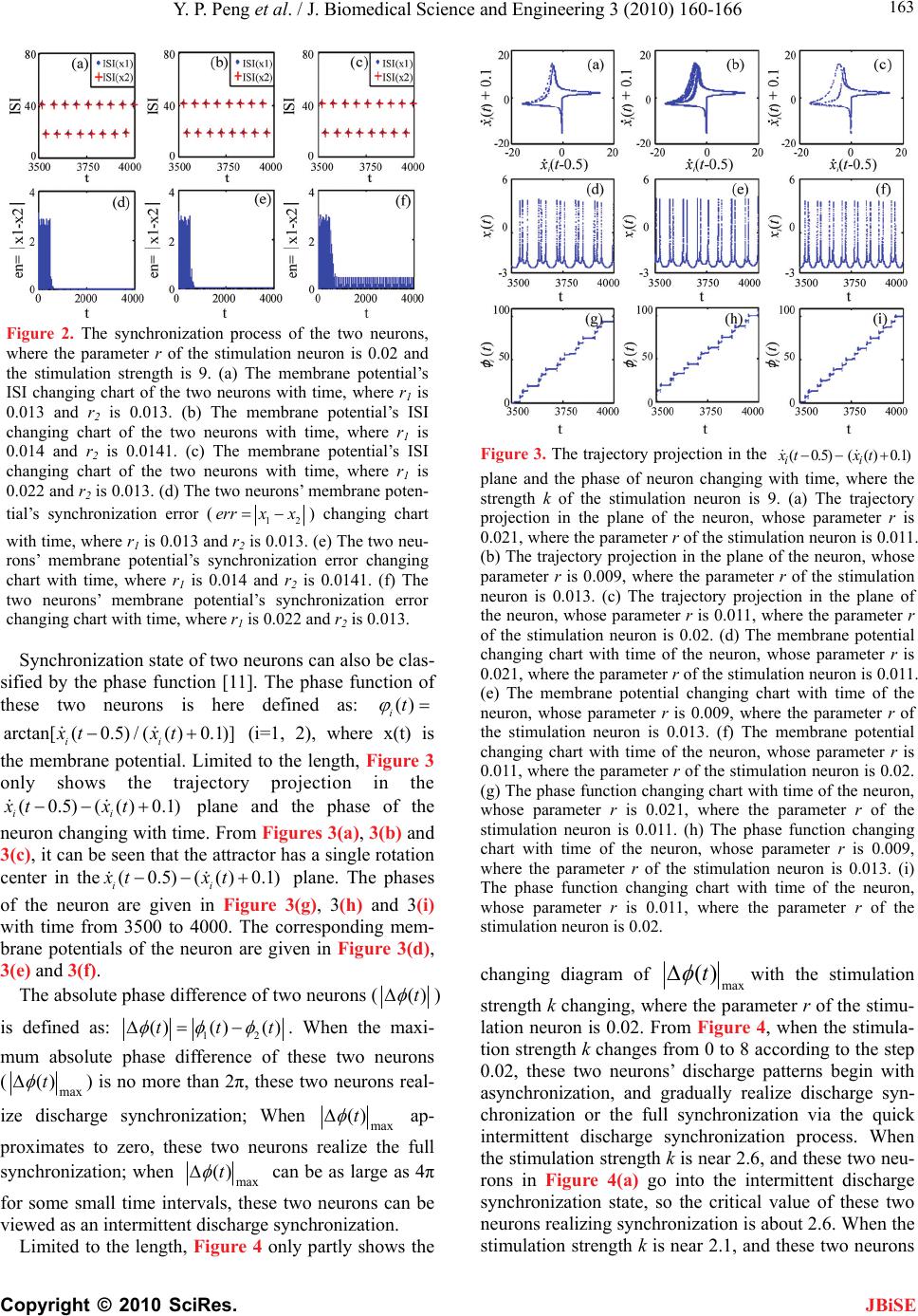

Y. P. Peng et al. / J. Biomedical Science and Engineering 3 (2010) 160-166
163
JBiSE
Figure 2. The synchronization process of the two neurons,
where the parameter r of the stimulation neuron is 0.02 and
the stimulation strength is 9. (a) The membrane potential’s
ISI changing chart of the two neurons with time, where r1 is
0.013 and r2 is 0.013. (b) The membrane potential’s ISI
changing chart of the two neurons with time, where r1 is
0.014 and r
2 is 0.0141. (c) The membrane potential’s ISI
changing chart of the two neurons with time, where r1 is
0.022 and r2 is 0.013. (d) The two neurons’ membrane poten-
tial’s synchronization error (12 errx x) changing chart
with time, where r1 is 0.013 and r2 is 0.013. (e) The two neu-
rons’ membrane potential’s synchronization error changing
chart with time, where r1 is 0.014 and r2 is 0.0141. (f) The
two neurons’ membrane potential’s synchronization error
changing chart with time, where r1 is 0.022 and r2 is 0.013.
Synchronization state of two neurons can also be clas-
sified by the phase function [11]. The phase function of
these two neurons is here defined as: ()
it


(i=1, 2), where x(t) is
the membrane potential. Limited to the length, Figure 3
only shows the trajectory projection in the
plane and the phase of the
neuron changing with time. From Figures 3(a), 3(b) and
3(c), it can be seen that the attractor has a single rotation
center in the plane. The phases
of the neuron are given in Figure 3(g), 3(h) and 3(i)
with time from 3500 to 4000. The corresponding mem-
brane potentials of the neuron are given in Figure 3(d),
3(e) and 3(f).
arctan[(0.5) / (()0.1)]
ii
xt xt

(0.5)(()0.1)
ii
xt xt 

(0.5)((
i
xt xt
)0.1)
i


The absolute phase difference of two neurons (()t
 )
is defined as: 12 ()()()tt   t. When the maxi-
mum absolute phase difference of these two neurons
(max )(t  ) is no more than 2π, these two neurons real-
ize discharge synchronization; When max )(t   ap-
proximates to zero, these two neurons realize the full
synchronization; when max )(t   can be as large as 4π
for some small time intervals, these two neurons can be
viewed as an intermittent discharge synchronization.
Limited to the length, Figure 4 only partly shows the
Figure 3. The trajectory projection in the

)5.0(txi
( )1.0)(

txi

plane and the phase of neuron changing with time, where the
strength k of the stimulation neuron is 9. (a) The trajectory
projection in the plane of the neuron, whose parameter r is
0.021, where the parameter r of the stimulation neuron is 0.011.
(b) The trajectory projection in the plane of the neuron, whose
parameter r is 0.009, where the parameter r of the stimulation
neuron is 0.013. (c) The trajectory projection in the plane of
the neuron, whose parameter r is 0.011, where the parameter r
of the stimulation neuron is 0.02. (d) The membrane potential
changing chart with time of the neuron, whose parameter r is
0.021, where the parameter r of the stimulation neuron is 0.011.
(e) The membrane potential changing chart with time of the
neuron, whose parameter r is 0.009, where the parameter r of
the stimulation neuron is 0.013. (f) The membrane potential
changing chart with time of the neuron, whose parameter r is
0.011, where the parameter r of the stimulation neuron is 0.02.
(g) The phase function changing chart with time of the neuron,
whose parameter r is 0.021, where the parameter r of the
stimulation neuron is 0.011. (h) The phase function changing
chart with time of the neuron, whose parameter r is 0.009,
where the parameter r of the stimulation neuron is 0.013. (i)
The phase function changing chart with time of the neuron,
whose parameter r is 0.011, where the parameter r of the
stimulation neuron is 0.02.
changing diagram of max )(t  with the stimulation
strength k changing, where the parameter r of the stimu-
lation neuron is 0.02. From Figure 4, when the stimula-
tion strength k changes from 0 to 8 according to the step
0.02, these two neurons’ discharge patterns begin with
asynchronization, and gradually realize discharge syn-
chronization or the full synchronization via the quick
intermittent discharge synchronization process. When
the stimulation strength k is near 2.6, and these two neu-
rons in Figure 4(a) go into the intermittent discharge
synchronization state, so the critical value of these two
neurons realizing synchronization is about 2.6. When the
stimulation strength k is near 2.1, and these two neurons

Y. P. Peng et al. / J. Biomedical Science and Engineering 3 (2010) 160-166
164
in Figure 4(b) go into the intermittent discharge syn-
chronization state, so the critical value of these two neu-
rons realizing synchronization is about 2.1. When the
stimulation strength k is near 2.5, and these two neurons
in Figure 4(c) go into the intermittent discharge syn-
chronization state, so the critical value of these two neu-
rons realizing synchronization is about 2.5. When the
stimulation strength k is near 2, and these two neurons in
Figure 4(d) go into the intermittent discharge synchro-
nization state, so the critical value of these two neurons
realizing synchronization is about 2. When the stimula-
tion strength k is near 2.9, and these two neurons in
Figure 4(e) go into the intermittent discharge synchro-
nization state, so the critical value of these two neurons
realizing synchronization is about 2.9. So, under the
same stimulation signal, the stimulation strength’s criti-
cal value of the two neurons whose parameter r is at
0.008~0.009, is bigger than that of the two neurons
whose parameter r is at 0.0125~0.015. Under the same
stimulation signal, the less the difference between the
two neurons is the smaller stimulation strength k of the
two neurons’ realizing synchronization and the easier the
two neurons realize synchronization. In addition, the
bigger the stimulation strength k is easier the neurons
realize synchronization.
is the same, namely gradually evolves into the chaos
discharge pattern which is the same as the stimulation
neuron’s. When the stimulation strength is 0.5 and 1,
these two neurons don’t realize synchronization, and
when the stimulation strength is 3, 6, 9 and 12, these two
neurons realize discharge synchronization or the full
synchronization. When the stimulation strength is 2,
these two neurons except r1=0.009 and r2=0.021, r
1=
0.022 and r2=0.013, realize discharge synchronization or
the full synchronization. When the parameter r is the
same, these two neurons realize the full synchronization.
When the parameter r is a little different, these two neu-
rons realize the full synchronization or discharge syn-
chronization. When the parameter r is much different,
these two neurons realize discharge synchronization or
the approximate full synchronization. The synchroniza-
tion discharge pattern is the same as the stimulation neu-
ron’s discharge pattern (the chaos).
The parameter r of the stimulation neuron is 0.013
(the discharge pattern is the chaos). As it begins to
stimulate the two neurons, in above all cases, the two
uncouple neurons’ discharge patterns totally change into
dynamic period discharge pattern from the initial dis-
charge patterns with the stimulation strength k increasing,
and the changing trend of their membrane potentials’ ISI
is the same, namely gradually evolves into the chaos
discharge pattern which is the same as the stimulation
neuron’s. When the stimulation strength is 0.5 and 1,
these two neurons don’t realize synchronization, and
when the stimulation strength is 3, 6, 9 and 12, these two
neurons realize discharge synchronization or the full
synchronization. When the stimulation strength is 2,
only several groups of these two neurons realize dis-
charge synchronization or the full synchronization.
When the parameter r is the same, these two neurons
realize the full synchronization. When the parameter r is
a little different, these two neurons realize the full syn-
chronization or discharge synchronization. When the
parameter r is much different, these two neurons realize
discharge synchronization or the approximate full syn-
chronization. The synchronization discharge pattern is
3.2. Synchronization under the Stimulation of
the Chaos Discharge Pattern
The values of the parameters of these two uncoupled
neurons are above given values. The parameter r of the
stimulation neuron is respectively 0.0085 and 0.013, and
its discharge pattern is the chaos. Under each parameter
r, the stimulation strength k is respectively 0.5, 1, 2, 3, 6,
9, and 12.
The parameter r of the stimulation neuron is 0.0085
(the discharge pattern is the chaos). As it begins to
stimulate the two neurons, in above all cases, the two
uncouple neurons’ discharge patterns totally change into
dynamic period discharge pattern from the initial dis-
charge patterns with the stimulation strength k increasing,
and the changing trend of their membrane potentials’ ISI
Figure 4. The changing diagram ofmax )(t  is changing with the stimulation strength k changing, where the parameter r of
the stimulation neuron is 0.02, and the changing step of the stimulation strength k is 0.02. (a) The parameter r of these two
neurons is the same: r1=r2=0.009. (b) The parameter r of these two neurons is the same: r1=r2=0.013. (c) The parameter r of
these two neurons is a little different: r1=0.0085 and r2=0.009. (d) The parameter r of these two neurons is a little different:
r1=0.014 and r2=0.0141. (e) The parameter r of these two neurons is much different: r1=0.014 and r2=0.0085.
JBiSE

Y. P. Peng et al. / J. Biomedical Science and Engineering 3 (2010) 160-166
165
JBiSE
Figure 5. The synchronization process of the two neurons,
where the parameter r of the stimulation neuron is 0.013 and
the stimulation strength k is 9. (a) The membrane potential’s
ISI changing chart of the two neurons with time, where r1 is
0.013 and r2 is 0.013. (b) The membrane potential’s ISI
changing chart of the two neurons with time, where r1 is
0.014 and r2 is 0.0141. (c) The membrane potential’s ISI
changing chart of the two neurons with time, where r1 is
0.022 and r2 is 0.013. (d) The two neurons’ membrane po-
tential’s synchronization error (21 xxerr  ) changing chart
with time, where r1 is 0.013 and r2 is 0.013. (e) The two
neurons’ membrane potential’s synchronization error chang-
ing chart with time, where r1 is 0.014 and r2 is 0.0141. (f)
The two neurons’ membrane potential’s synchronization er-
ror changing chart with time, where r1 is 0.022 and r2 is
0.013.
the same as the stimulation neuron’s discharge pattern
(the chaos).
Limited to the length, Figure 5 only shows the syn-
chronization process of the two neurons. In Figure 5,
from (a) and (d), (b) and (e), (c) and (f), these two neu-
rons respectively realize the full synchronization, the full
synchronization, and the discharge synchronization; and
the synchronization discharge pattern is all the chaos,
which is the same as the stimulation neuron’s discharge
pattern.
Limited to the length, Figure 6 only shows the chang-
ing diagram of max
)(t   with the stimulation strength k
changing. From Figure 6, when the stimulation strength
k changes from 0 to 8 according to the step 0.02, these
two neurons’ discharge patterns begin with asynchroni-
zation, and gradually realize discharge synchronization
or the full synchronization via the quick intermittent
discharge synchronization process.
When the stimulation strength k is near 1.7, and these
two neurons in Figure 6(a) go into the intermittent dis-
charge synchronization state, so the critical value of
these two neurons realizing synchronization is about 1.7.
When the stimulation strength k is near 1.3, and these
two neurons in Figure 6(b) go into the intermittent dis-
charge synchronization state, so the critical value of
these two neurons realizing synchronization is about 1.3.
When the stimulation strength k is near 1.6, and these
two neurons in Figure 6(c) go into the intermittent dis-
charge synchronization state, so the critical value of
these two neurons realizing synchronization is about 1.6.
When the stimulation strength k is near 1.4, and these
two neurons in Figure 6(d) go into the intermittent dis-
charge synchronization state, so the critical value of
these two neurons realizing synchronization is about 1.4.
When the stimulation strength k is near 1.8, and these
two neurons in Figure 6(e) go into the intermittent dis-
charge synchronization state, so the critical value of
these two neurons realizing synchronization is about 1.8.
So, under the same stimulation signal, the stimulation
strength’s critical value of the two neurons whose pa-
rameter r is at 0.008~0.009, is bigger than that of the two
neurons whose parameter r is at 0.0125~0.015. Under
the same stimulation signal, the less the difference be-
tween the two neurons is, the smaller the stimulation
strength k of the two neurons’ realizing synchronization
is, and the easier the two neurons realize synchronization.
From Figures 4 and 6, for the two neurons, the critical
value of the chaos signal’s stimulation strength is less
than that of the period signal’s stimulation strength, so
the chaos signal’s stimulation is easier to realize the
synchronization of two neurons than the period signal’s
stimulation. In addition, the bigger the stimulation str-
ength k is, the easier the neurons realize synchronization.
Figure 6. The changing diagram of max )(t   is changing with the stimulation strength k, where the parameter r of the
stimulation neuron is 0.0085, and the changing step of the stimulation strength k is 0.02. (a) The parameter r of these two
neurons is the same: r1=r2=0.009. (b) The parameter r of these two neurons is the same: r1=r2=0.013. (c) The parameter r
of these two neurons is a little different: r1=0.0085 and r2=0.009. (d) The parameter r of these two neurons is a little dif-
ferent: r1=0.014 and r2=0.0141. (e) The parameter r of these two neurons is much different: r1=0.014 and r2=0.0085.

Y. P. Peng et al. / J. Biomedical Science and Engineering 3 (2010) 160-166
166
JBiSE
4. CONCLUSIONS
Under the stimulation of the neuron’s membrane poten-
tial whose discharge pattern is period or the chaos, the
two uncoupled neurons under different initial conditions,
whose parameter r is different or the same, can realize
the full synchronization or discharge synchronization,
and can only be synchronized to the response being in
synchronization with stimulation signal. The synchroni-
zation discharge patterns are the same as the stimulation
neuron, and the synchronization characteristics are
mainly related to the discharge pattern and the strength
of the stimulation neuron’s membrane potential, and are
little related to the parameter r and the initial state of the
two uncoupled neurons. And the bigger the strength of
the stimulation signal is, the easier the two neurons real-
ize synchronization. The critical strength value of these
two neurons realizing synchronization is related to, not
only the two neurons’ parameter r and the initial state,
but also the stimulation signal. For the two neurons, the
critical value of the chaos signal’s stimulation strength is
less than that of the period signal’s stimulation strength.
The chaos signal’s stimulation is easier to realize syn-
chronization of two neurons than the period signal’s
stimulation.
This investigation shows characteristics of the neu-
ron’s membrane potential affecting the synchronization
process of two uncoupled neurons, and the two neurons’
discharge patterns and synchronization process can be
adjusted and controlled by the discharge pattern and the
strength of the stimulation neuron’s membrane potential.
This result is helpful to study synchronization and en-
code of many neurons or neural network.
5. ACKNOWLEDGEMENTS
The authors would like to thank “The Journal of Biomedical Science
and Engineering” for providing the chance and really appreciate the
anonymous reviewers for the valuable comments on the paper.
REFERENCES
[1] Pecora, L.M. and Carroll, T.L. (1990) Synchronization in
chaotic systems. Physical Review Letter, 64, 821-824.
[2] Pecora, L.M. and Carroll, T.L. (1991) Driving systems
with chaotic signals. Physical Review: A, 44, 2374-2383.
[3] Gray, C.M. et al. (1989) Oscillatory response in cat
visual cortex exhibit inter-columnar synchronization
which reflects global stimulus properties. Nature, 338,
334-337.
[4] Hindmarsh, J.L. and Rose, R.M. (1982) A model of the
nerve impulse using two first-order differential equation.
Nature, 296, 162-165.
[5] Hindmarsh, J.L. and Rose, R.M. (1984) A Model of
neuronal bursting using three coupled first order diffe-
rential equations. Series B, Biological Sciences, 221,
87-102.
[6] Peng, Y.P., Jian, Z. and Wang, J. (2006) Study on dis-
charge patterns of Hindmarsh-Rose neurons under slow
wave current stimulation. Lecture Notes in Computer
Science, 4221, 127-134.
[7] Huerta, R. and Rabinovich, M.I. (1997) Spike-train
bifurcation in two coupled chaotic neurons. Physical
Review: E, 55, R2108-R2110.
[8] Wu, Y. et al. (2005) Study on nonlinear characteristic of
two synchronizing uncoupled Hindmarsh-Rose neurons.
Physics Letters: A, 54, 3457-3464.
[9] He, D.H., Shi, P.L. and Stone, L. (2003) Noise-induced
synchronization in realistic models. Physical Review: E,
67, 0272011-0272013.
[10] Wu, Y. et al. (2005) Complete synchronization and phase
synchronization of two uncoupled neurons through para-
metrical drive. Journal of Xi’an Jiaotong University, 39,
544-547.
[11] Shuai, J.W. and Durand, D.M. (1999) Phase synchro-
nization in two coupled chaotic neurons. Physics Letters:
A, 264, 289-296.
[12] Peng, Y.P., Wang, J. and Jian, Z. (2009) Synchrony of
two uncoupled neurons under half wave sine current
stimulation. Communications in Nonlinear Science and
Numerical Simulation, 14, 1570-1575.
[13] Peng, Y.P. and Wang, J. (2007) Discharge patterns’
change of Hindmarsh-Rose neurons under slow ramp
current stimulation. BIC-TA IEEE, 52-55.
[14] Shi, X. and Lu, Q.S. (2005) Coherence resonance and
synchronization of Hindmarsh-Rose neurons with noise.
Chinese Physics, 14(6), 1088-1094.
[15] Wu, Y., Xu, J.X., He, D.H. and David, J.D. Earn (2005)
Generalized synchronization induced by noise and para-
meter mismatching in Hindmarsh-Rose neurons. Chaos,
Solitons and Fractals, 23, 1605-1611.
[16] Katsutoshi, Y., Keijin, S. and Atsushi, S. (2006) Noise-
induced synchronization of uncoupled nonlinear systems.
Journal of Sound and Vibration, 290, 34-47.
[17] Wu, Y., Xu, J.X., Jin, W.Y. and Hong, L. (2007) Detec-
tion of mechanism of noise-induced synchronization be-
tween two identical uncoupled neurons. Chin. Phys. Lett,
24(11), 3066-3069.