Energy and Power Engineering, 2010, 65-72
doi:10.4236/epe.2010.21010 Published Online February 2010 (http://www.scirp.org/journal/epe)
Scaling Laws for Plasma Focus Machines from
Numerical Experiments
S. H. SAW1,2, S. LEE1,2,3
1INTI University College, Nilai, Malaysia
2Institute for Plasma Focus Studies, 32 Oakpark Drive, Chadstone, Australia
3NSSE, National Institute of Education, Nanyang Technological University, Singapore
Abstract: Numerical experiments carried out systematically using the Lee Model code unveil insightful and
practical wide-ranging scaling laws for plasma focus machines for nuclear fusion energy as well as other ap-
plications. An essential feature of the numerical experiments is the fitting of a measured current waveform to
the computed waveform to calibrate the model for the particular machine, thus providing a reliable and rig-
orous determination of the all-important pinch current. The thermodynamics and radiation properties of the
resulting plasma are then reliably determined. This paper provides an overview of the recently published
scaling laws for neutron (Yn) and neon soft x-ray, SXR (Ysxr) yields:
Yn = 3.2x1011 Ipinch
4.5; Yn = 1.8x1010 Ipeak 3.8; Ipeak (0.3 to 5.7), Ipinch (0.2 to 2.4) in MA.
Yn~E0
2.0 at tens of kJ to Yn~E0 0.84 at MJ level (up to 25MJ) and
Ysxr = 8.3x103 Ipinch
3.6; Ysxr = 6x102 Ipeak 3.2; Ipeak (0.1 to 2.4), Ipinch (0.07 to1.3) in MA.
Ysxr~E0
1.6 (kJ range) to Ysxr~E0 0.8 (towards MJ).
Keywords: dense plasma focus, plasma focus scaling laws, neutron scaling laws, soft x-ray scaling laws,
plasma focus modeling, Lee model code
1. Introduction
Plasma focus machines of various energies are increas-
ingly being studied as sources of neutrons and soft x-rays.
The most exciting prospect is for scaling the plasma focus
up to regimes relevant for fusion energy studies. However,
even a simple machine such as the UNU/ICTP PFF 3 kJ
machine consistently produces 108 neutrons when oper-
ated in deuterium [1]. Plasma focus machines operated in
neon have also been studied as intense sources of soft
x-rays with potential applications [2–4]. Whilst many
recent experiments have concentrated efforts on low en-
ergy devices [2–4] with a view of operating these as re-
petitive pulsed sources, other experiments have looked at
x-ray pulses from larger plasma focus devices [5,6] ex-
tending to the MJ regime. Numerical experiments simu-
lating x-ray pulses from plasma focus devices are also
gaining more interest in the public domain. For example,
the Institute of Plasma Focus Studies [7] conducted a
recent international Internet Workshop on Plasma Focus
Numerical Experiments [8], at which it was demon-
strated that the Lee model code [9] not only computes
realistic focus pinch parameters, but also absolute values
of neutron yield Yn and soft x-ray yield Ysxr which are
consistent with those measured experimentally. A com-
parison was made for the case of the NX2 machine [4],
showing good agreement between computed and meas-
ured Ysxr as a function of P0 [8,10]. This gives confidence
that the Lee model code gives realistic results in the
computation of Yn and Ysxr.
In this paper, we show the comprehensive range of
numerical experiments conducted to derive scaling laws
on neutron yield Yn [11,12] and neon Ysxr, in terms of
storage energy E0, peak discharge current Ipeak and peak
focus pinch current Ipinch obtained from studies carried
out over E0 varying from 0.2 kJ to 25 MJ for optimised
machine parameters and operating parameters. It is worth
mentioning that the scaling laws in terms of Ipinch and Ipeak
have also been obtained for numerical experiments using
the Lee model code fitted with the actual machine pa-
rameters and operating parameters and the difference
from that obtained for the optimised conditions are within
the order of 0.1 in the scaling laws power factor for neu-
trons and no change for neon SXR yield with Ipinch.
We also wish to point out that the distinction of Ipinch
from Ipeak is of basic importance [13–15]. The scaling
with Ipinch is the more fundamental and robust one; since
obviously there are situations (no pinching or poor
pinching however optimized) where Ipeak may be large
but Yn is zero or small; whereas the scaling with Ipinch is

S. H. SAW ET AL.
66
certainly more consistent with all situations. In these
works the primary importance of Ipinch for scaling plasma
focus properties including neutron yield Yn, has been
firmly established [11–15].
2. The Lee Model Code
The Lee model code couples the electrical circuit with
plasma focus dynamics, thermodynamics and radiation,
enabling realistic simulation of all gross focus properties.
The basic model, described in 1984 [16] was success-
fully used to assist several projects [17–19]. Radiation-
coupled dynamics was included in the five-phase code
leading to numerical experiments on radiation cooling
[20]. The vital role of a finite small disturbance speed
discussed by Potter in a Z-pinch situation [21] was in-
corporated together with real gas thermodynamics and
radiation-yield terms. Before this ‘communication delay
effect’ was incorporated, the model consistently over-
estimated the radial speeds. This is serious from the point
of view of neutron yields. A factor of two in shock
speeds gives a factor of four in temperatures leading to a
difference in fusion cross-sections of~1000 at the range
of temperatures we are dealing with. This version of the
code assisted other research projects [22–27] and was
web-published in 2000 [28] and 2005 [29]. Plasma
self-absorption was included in 2007 [27] improving
SXR yield simulation. The code has been used exten-
sively in several machines including UNU/ICTP PFF [1,
17,22,23,25–27,30,31], NX2 [24,27,32], NX1 [3,32] and
adapted for the Filippov-type plasma focus DENA [33].
A recent development is the inclusion of the neutron
yield Yn using a beam–target mechanism [11,12,14,15,
34], incorporated in recent versions [9] of the code (ver-
sions later than RADPFV5.13), resulting in realistic Yn
scaling with Ipinch [11,12]. The versatility and utility of
the model are demonstrated in its clear distinction of
Ipinch from Ipeak [13] and the recent uncovering of a
plasma focus pinch current limitation effect [14,15]. The
description, theory, code and a broad range of results of
this ‘Universal Plasma Focus Laboratory Facility’ are
available for download from [9].
A brief description of the code is given below. The
five phases are summarised as follows:
1) Axial Phase: Described by a snowplow model with
an equation of motion coupled to a circuit equation. The
equation of motion incorporates the axial phase model
parameters: mass and current factors fm and fc respec-
tively. The mass swept-up factor fm accounts for not only
the porosity of the current sheet but also for the inclina-
tion of the moving current sheet-shock front structure
and all other unspecified effects which have effects
equivalent to increasing or reducing the amount of mass
in the moving structure during the axial phase. The cur-
rent factor fc accounts for the fraction of current effec-
tively flowing in the moving structure (due to all effects
such as current shedding at or near the back-wall and
current sheet inclination). This defines the fraction of
current effectively driving the structure during the axial
phase.
2) Radial Inward Shock Phase: Described by four
coupled equations using an elongating slug model. The
first equation computes the radial inward shock speed
from the driving magnetic pressure. The second equation
computes the axial elongation speed of the column. The
third equation computes the speed of the current sheath,
also called the magnetic piston, allowing the current
sheath to separate from the shock front by applying an
adiabatic approximation. The fourth is the circuit equa-
tion. Thermodynamic effects due to ionization and exci-
tation are incorporated into these equations, these effects
being important for gases other than hydrogen and deu-
terium. Temperature and number densities are computed
during this phase. A communication delay between shock
front and current sheath due to the finite small distur-
bance speed is crucially implemented in this phase. The
model parameters, radial phase mass swept-up and cur-
rent factors fmr and fcr respectively are incorporated in all
three radial phases. The mass swept-up factor fmr ac-
counts for all mechanisms which have effects equivalent
to increasing or reducing the amount of mass in the
moving slug during the radial phase. The current factor
fcr accounts for the fraction of current effectively flowing
in the moving piston forming the back of the slug (due to
all effects). This defines the fraction of current effec-
tively driving the radial slug.
3) Radial Reflected Shock (RS) Phase: When the
shock front hits the axis, because the focus plasma is
collisional, a reflected shock develops which moves ra-
dially outwards, whilst the radial current sheath piston
continues to move inwards. Four coupled equations are
also used to describe this phase, these being for the re-
flected shock moving radially outwards, the piston mov-
ing radially inwards, the elongation of the annular col-
umn and the circuit. The same model parameters fmr and
fcr are used as in the previous radial phase. The plasma
temperature behind the RS undergoes a jump by a factor
of approximately two.
4) Slow Compression (Quiescent) or Pinch Phase:
When the out-going reflected shock hits the in-coming
piston the compression enters a radiative phase, in which
for gases such as neon radiation emission may actually
enhance the compression, where we have included en-
ergy loss/gain terms from Joule heating and radiation
losses into the piston equation of motion. Three coupled
equations describe this phase; these being the piston ra-
dial motion equation, the pinch column elongation equa-
tion and the circuit equation, incorporating the same
model parameters as in the previous two phases. Ther-
modynamic effects are incorporated into this phase. The
duration of this slow compression phase is set as the time

S. H. SAW ET AL.
67
of transit of small disturbances across the pinched plas-
ma column. The computation of this phase is terminated
at the end of this duration.
4) Expanded Column Phase: To simulate the current
trace beyond this point, we allow the column to suddenly
attain the radius of the anode, and use the expanded
column inductance for further integration. In this final
phase the snowplow model is used, and two coupled
equations are used; similar to the axial phase above. This
phase is not considered important as it occurs after the
focus pinch.
2.1 Computation of Neutron Yield
The neutron yield is computed using a phenomenological
beam-target neutron generating mechanism described
recently by Gribkov et al [34] and adapted to yield the
following equation. A beam of fast deuteron ions is pro-
duced by diode action in a thin layer close to the anode,
with plasma disruptions generating the necessary high
voltages. The beam interacts with the hot dense plasma
of the focus pinch column to produce the fusion neutrons.
The beam-target yield is derived [11,12,14,28] as:
Yb-t= Cn ni Ipinch
2zp 2(ln (b/rp) σ/U0.5 (1)
where ni is the ion density, b is the cathode radius, rp is
the radius of the plasma pinch with length zp, σ the
cross-section of the D-D fusion reaction, n- branch [35]
and U, the beam energy. Cn is treated as a calibration
constant combining various constants in the derivation
process.
The D-D cross-section is sensitive to the beam en-
ergy in the range 15–150kV; so it is necessary to use
the appropriate range of beam energy to compute σ.
The code computes induced voltages (due to current
motion inductive effects) Vmax of the order of only
15–50 kV. However it is known, from experiments that
the ion energy responsible for the beam-target neutrons
is in the range 50–150 keV [34], and for smaller lower-
voltage machines the relevant energy could be lower at
30–60 keV [31]. Thus in line with experimental obser-
vations the D-D cross section σ is reasonably obtained
by using U=3Vmax. This fit was tested by using U equal
to various multiples of Vmax. A reasonably good fit of
the computed neutron yields to the measured published
neutron yields at energy levels from sub-kJ to near MJ
was obtained when the multiple of 3 was used; with
poor agreement for most of the data points when for
example a multiple of 1 or 2 or 4 or 5 was used. The
model uses a value of Cn=2.7x107 obtained by cali-
brating the yield [9,13,14] at an experimental point of
0.5 MA.
The thermonuclear component is also computed in
every case and it is found that this component is negligible
when compared with the beam-target component.
2.2 Computation of Neon SXR Yield
We note that the transition from Phase 4 to Phase 5 is
observed in laboratory measurements to occur in an ex-
tremely short time with plasma/current disruptions re-
sulting in localized regions of high densities and tem-
peratures. These localized regions are not modelled in
the code, which consequently computes only an average
uniform density, and an average uniform temperature
which are considerably lower than measured peak den-
sity and temperature. However, because the 4 model pa-
rameters are obtained by fitting the computed total cur-
rent waveform to the measured total current waveform,
the model incorporates the energy and mass balances
equivalent, at least in the gross sense, to all the processes
which are not even specifically modelled. Hence the
computed gross features such as speeds and trajectories
and integrated soft x-ray yields have been extensively
tested in numerical experiments for several machines and
are found to be comparable with measured values.
In the code [9], neon line radiation QL is calculated as
follows:
TzrZZnx
d
t
dQ
fpni
L/)(106.4 24231


 (2)
where for the temperatures of interest in our experiments
we take the SXR yield Ysxr = QL. Zn is the atomic number.
Hence the SXR energy generated within the plasma
pinch depends on the properties: number density ni, ef-
fective charge number Z, pinch radius rp, pinch length zf
and temperature T. It also depends on the pinch duration
since in our code the QL is obtained by integrating over
the pinch duration.
This generated energy is then reduced by the plasma
self-absorption which depends primarily on density and
temperature; the reduced quantity of energy is then emit-
ted as the SXR yield. These effects are included in the
modelling by computing volumetric plasma
self-absorption factor A derived from the photonic exci-
tation number M which is a function of Zn, ni, Z and T.
However, in our range of operation, the numerical ex-
periments show that the self absorption is not significant.
It was first pointed out by Liu Mahe [23] that a tempera-
ture around 300 eV is optimum for SXR production.
Shan Bing’s subsequent work [24] and our experience
through numerical experiments suggest that around
2x106 K (below 200 eV) or even a little lower could be
better. Hence unlike the case of neutron scaling, for SXR
scaling there is an optimum small range of temperatures
(T windows) to operate.
3. Numerical Experiments
The Lee code is configured to work as any plasma focus
by inputting the bank parameters, L0, C0 and stray circuit
resistance r0; the tube parameters b, a and z0 and opera-
tional parameters V0 and P0 and the fill gas. The standard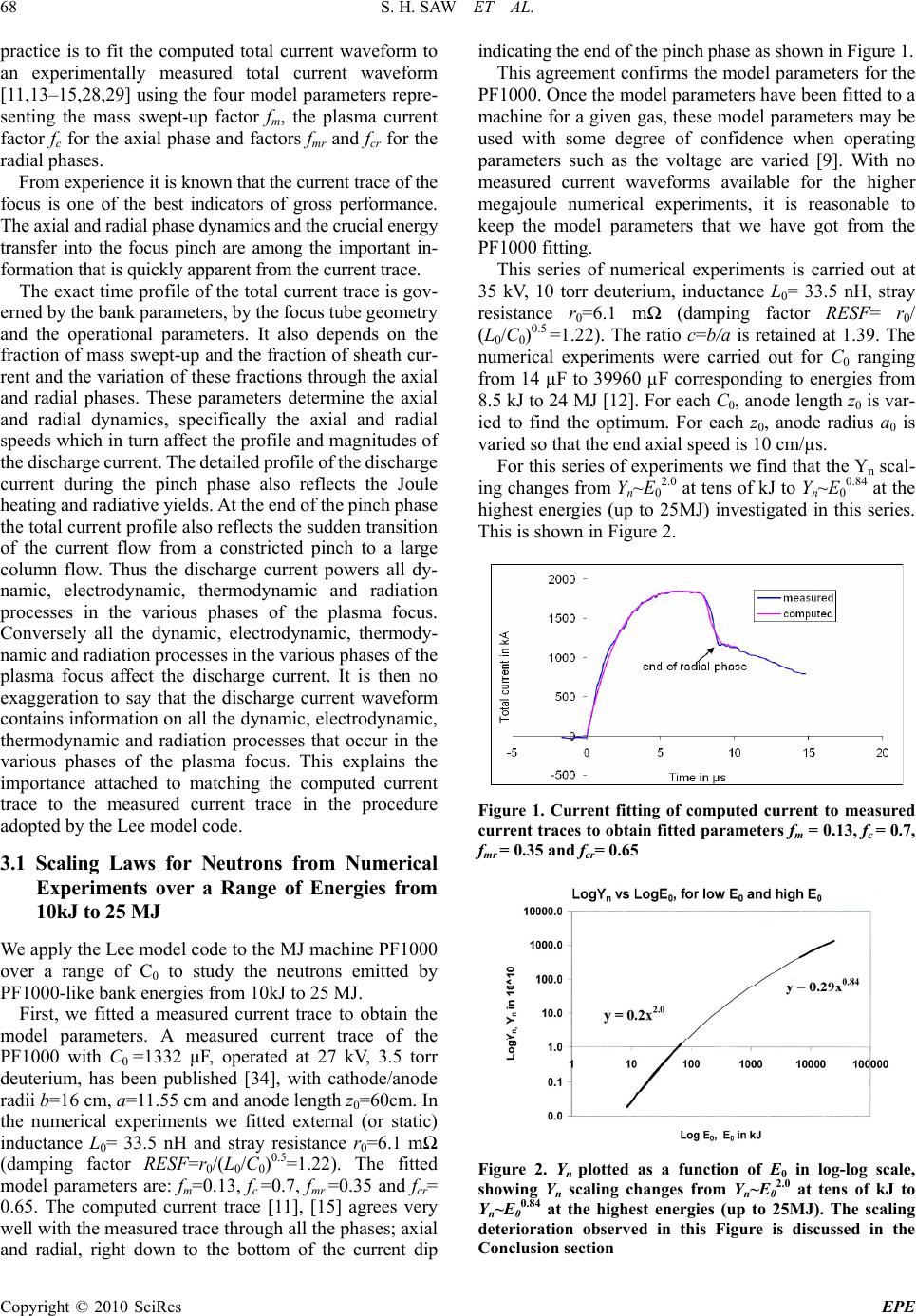

S. H. SAW ET AL.
68
practice is to fit the computed total current waveform to
an experimentally measured total current waveform
[11,13–15,28,29] using the four model parameters repre-
senting the mass swept-up factor fm, the plasma current
factor fc for the axial phase and factors fmr and fcr for the
radial phases.
From experience it is known that the current trace of the
focus is one of the best indicators of gross performance.
The axial and radial phase dynamics and the crucial energy
transfer into the focus pinch are among the important in-
formation that is quickly apparent from the current trace.
The exact time profile of the total current trace is gov-
erned by the bank parameters, by the focus tube geometry
and the operational parameters. It also depends on the
fraction of mass swept-up and the fraction of sheath cur-
rent and the variation of these fractions through the axial
and radial phases. These parameters determine the axial
and radial dynamics, specifically the axial and radial
speeds which in turn affect the profile and magnitudes of
the discharge current. The detailed profile of the discharge
current during the pinch phase also reflects the Joule
heating and radiative yields. At the end of the pinch phase
the total current profile also reflects the sudden transition
of the current flow from a constricted pinch to a large
column flow. Thus the discharge current powers all dy-
namic, electrodynamic, thermodynamic and radiation
processes in the various phases of the plasma focus.
Conversely all the dynamic, electrodynamic, thermody-
namic and radiation processes in the various phases of the
plasma focus affect the discharge current. It is then no
exaggeration to say that the discharge current waveform
contains information on all the dynamic, electrodynamic,
thermodynamic and radiation processes that occur in the
various phases of the plasma focus. This explains the
importance attached to matching the computed current
trace to the measured current trace in the procedure
adopted by the Lee model code.
3.1 Scaling Laws for Neutrons from Numerical
Experiments over a Range of Energies from
10kJ to 25 MJ
We apply the Lee model code to the MJ machine PF1000
over a range of C0 to study the neutrons emitted by
PF1000-like bank energies from 10kJ to 25 MJ.
First, we fitted a measured current trace to obtain the
model parameters. A measured current trace of the
PF1000 with C0 =1332 μF, operated at 27 kV, 3.5 torr
deuterium, has been published [34], with cathode/anode
radii b=16 cm, a=11.55 cm and anode length z0=60cm. In
the numerical experiments we fitted external (or static)
inductance L0= 33.5 nH and stray resistance r0=6.1 mΩ
(damping factor RESF=r0/(L0/C0)0.5=1.22). The fitted
model parameters are: fm=0.13, fc =0.7, fmr =0.35 and fcr=
0.65. The computed current trace [11], [15] agrees very
well with the measured trace through all the phases; axial
and radial, right down to the bottom of the current dip
indicating the end of the pinch phase as shown in Figure 1.
This agreement confirms the model parameters for the
PF1000. Once the model parameters have been fitted to a
machine for a given gas, these model parameters may be
used with some degree of confidence when operating
parameters such as the voltage are varied [9]. With no
measured current waveforms available for the higher
megajoule numerical experiments, it is reasonable to
keep the model parameters that we have got from the
PF1000 fitting.
This series of numerical experiments is carried out at
35 kV, 10 torr deuterium, inductance L0= 33.5 nH, stray
resistance r0=6.1 mΩ (damping factor RESF= r0/
(L0/C0)0.5 =1.22). The ratio c=b/a is retained at 1.39. The
numerical experiments were carried out for C0 ranging
from 14 µF to 39960 µF corresponding to energies from
8.5 kJ to 24 MJ [12]. For each C0, anode length z0 is var-
ied to find the optimum. For each z0, anode radius a0 is
varied so that the end axial speed is 10 cm/µs.
For this series of experiments we find that the Yn scal-
ing changes from Yn~E0
2.0 at tens of kJ to Yn~E0 0.84 at the
highest energies (up to 25MJ) investigated in this series.
This is shown in Figure 2.
Figure 1. Current fitting of computed current to measured
current traces to obtain fitted parameters fm = 0.13, fc = 0.7,
fmr = 0.35 and fcr= 0.65
Figure 2. Yn plotted as a function of E0 in log-log scale,
showing Yn scaling changes from Yn~E02.0 at tens of kJ to
Yn~E00.84 at the highest energies (up to 25MJ). The scaling
deterioration observed in this Figure is discussed in the
Conclusion section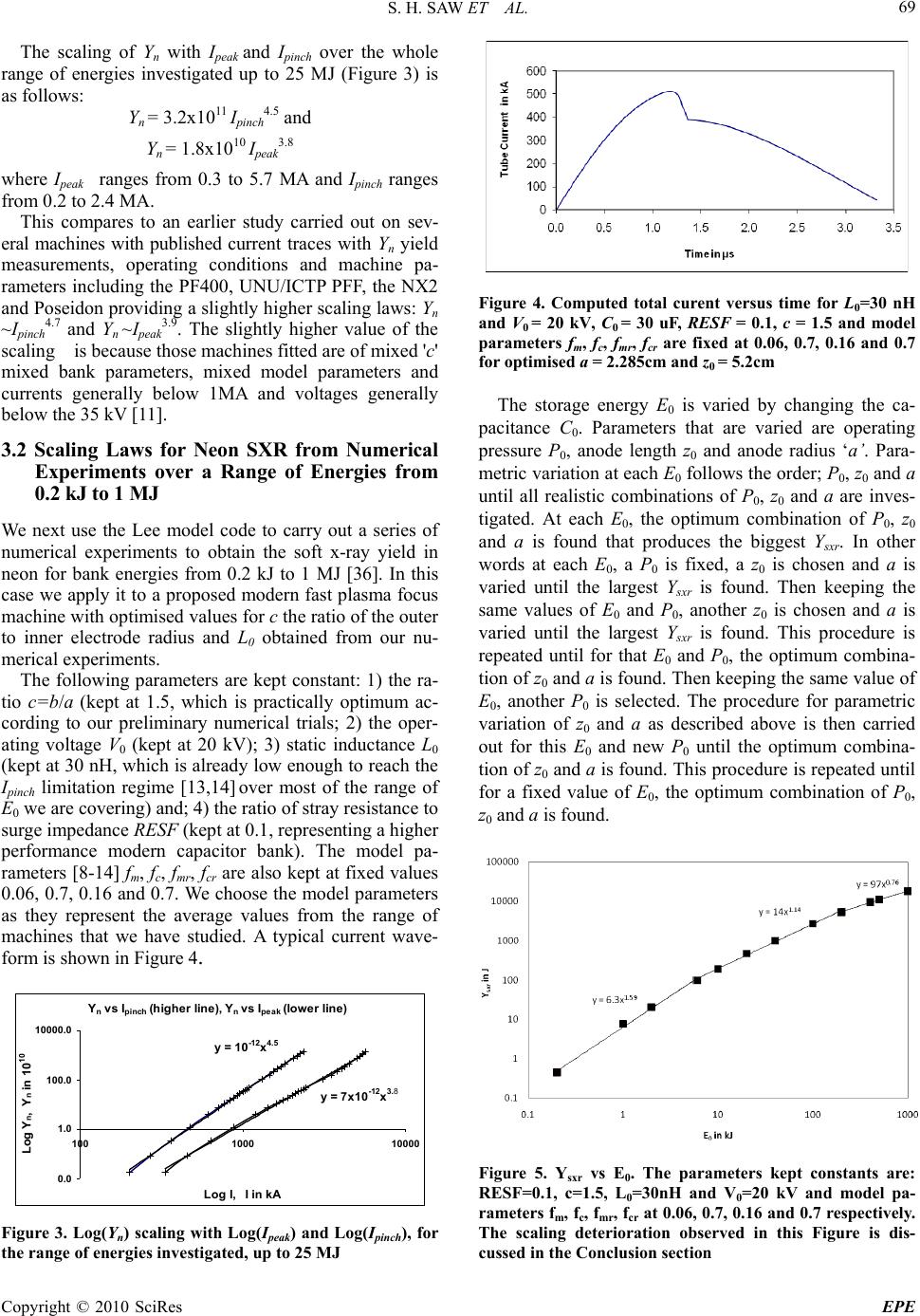

S. H. SAW ET AL.
69
The scaling of Yn with Ipeak and Ipinch over the whole
range of energies investigated up to 25 MJ (Figure 3) is
as follows:
Yn = 3.2x1011 Ipinch
4.5 and
Yn = 1.8x1010 Ipeak
3.8
where Ipeak ranges from 0.3 to 5.7 MA and Ipinch ranges
from 0.2 to 2.4 MA.
This compares to an earlier study carried out on sev-
eral machines with published current traces with Yn yield
measurements, operating conditions and machine pa-
rameters including the PF400, UNU/ICTP PFF, the NX2
and Poseidon providing a slightly higher scaling laws: Yn
~Ipinch
4.7 and Yn ~Ipeak 3.9. The slightly higher value of the
scaling is because those machines fitted are of mixed 'c'
mixed bank parameters, mixed model parameters and
currents generally below 1MA and voltages generally
below the 35 kV [11].
3.2 Scaling Laws for Neon SXR from Numerical
Experiments over a Range of Energies from
0.2 kJ to 1 MJ
We next use the Lee model code to carry out a series of
numerical experiments to obtain the soft x-ray yield in
neon for bank energies from 0.2 kJ to 1 MJ [36]. In this
case we apply it to a proposed modern fast plasma focus
machine with optimised values for c the ratio of the outer
to inner electrode radius and L0 obtained from our nu-
merical experiments.
The following parameters are kept constant: 1) the ra-
tio c=b/a (kept at 1.5, which is practically optimum ac-
cording to our preliminary numerical trials; 2) the oper-
ating voltage V0 (kept at 20 kV); 3) static inductance L0
(kept at 30 nH, which is already low enough to reach the
Ipinch limitation regime [13,14] over most of the range of
E0 we are covering) and; 4) the ratio of stray resistance to
surge impedance RESF (kept at 0.1, representing a higher
performance modern capacitor bank). The model pa-
rameters [8-14] fm, fc, fmr, fcr are also kept at fixed values
0.06, 0.7, 0.16 and 0.7. We choose the model parameters
as they represent the average values from the range of
machines that we have studied. A typical current wave-
form is shown in Figure 4.
Y
n
vs I
pinch
(higher line), Y
n
vs I
peak
(lower l i n e)
y = 10
-12
x
4.5
y = 7x10
-12
x
3.8
0.0
1.0
100.0
10000.0
1001000 10000
Log I, I in kA
Log Y
n
, Y
n
in 10
10
Figure 3. Log(Yn) scaling with Log(Ipeak) and Log(Ipinch), for
the range of energies investigated, up to 25 MJ
Figure 4. Computed total curent versus time for L0=30 nH
and V0 = 20 kV, C0 = 30 uF, RESF = 0.1, c = 1.5 and model
parameters fm, fc, fmr, fcr are fixed at 0.06, 0.7, 0.16 and 0.7
for optimised a = 2.285cm and z0 = 5.2cm
The storage energy E0 is varied by changing the ca-
pacitance C0. Parameters that are varied are operating
pressure P0, anode length z0 and anode radius ‘a’. Para-
metric variation at each E0 follows the order; P0, z0 and a
until all realistic combinations of P0, z0 and a are inves-
tigated. At each E0, the optimum combination of P0, z0
and a is found that produces the biggest Ysxr. In other
words at each E0, a P0 is fixed, a z0 is chosen and a is
varied until the largest Ysxr is found. Then keeping the
same values of E0 and P0, another z0 is chosen and a is
varied until the largest Ysxr is found. This procedure is
repeated until for that E0 and P0, the optimum combina-
tion of z0 and a is found. Then keeping the same value of
E0, another P0 is selected. The procedure for parametric
variation of z0 and a as described above is then carried
out for this E0 and new P0 until the optimum combina-
tion of z0 and a is found. This procedure is repeated until
for a fixed value of E0, the optimum combination of P0,
z0 and a is found.
Figure 5. Ysxr vs E0. The parameters kept constants are:
RESF=0.1, c=1.5, L0=30nH and V0=20 kV and model pa-
rameters fm, fc, fmr, fcr at 0.06, 0.7, 0.16 and 0.7 respectively.
The scaling deterioration observed in this Figure is dis-
cussed in the Conclusion section

S. H. SAW ET AL.
70
The procedure is then repeated with a new value of E0.
In this manner after systematically carrying out some
2000 runs, the optimized runs for various energies are
obtained. A plot Ysxr against E0 is shown in Figure 5.
We then plot Ysxr against Ipeak and Ipinch and obtain SXR
yield scales as Ysxr~Ipinch
3.6 and Ysxr~Ipeak 3.2. The Ipinch
scaling has less scatter than the Ipeak scaling. We next
subject the scaling to further test when the fixed parame-
ters RESF, c, L0 and V0 and model parameters fm, fc, fmr,
fcr are varied. We add in the results of some numerical
experiments using the parameters of several existing
plasma focus devices including the UNU/ICTP PFF
(RESF =0.2, c =3.4, L0 =110 nH and V0 =14 kV with fit-
ted model parameters fm = 0.05, fc = 0.7, fmr = 0.2, fcr = 0.8)
[7-9], [23], the NX2 (RESF = 0.1, c = 2.2, L0 = 20 nH
and V0 = 11 kV with fitted model parameters fm = 0.06, fc
= 0.7, fmr = 0.16, fcr = 0.7) [7–10,24] and PF1000 (RESF
= 0.1, c = 1.39, L0 = 33 nH and V0 = 27 kV with fitted
model parameters fm = 0.1, fc = 0.7, fmr = 0.15, fcr = 0.7)
[7–9,14]. These new data points (unblackened data
points in Figure 6) contain wide ranges of c, V0, L0 and
model parameters. The resulting Ysxr versus Ipinch log-log
curve remains a straight line, with the scaling index 3.6
unchanged and with no more scatter than before. How-
ever the resulting Ysxr versus Ipeak curve now exhibits
considerably larger scatter and the scaling index has
changed.
We would like to highlight that the consistent behav-
iour of Ipinch in maintaining the scaling of Ysxr ~ Ipinch
3.6
with less scatter than the Ysxr~Ipeak
3.2 scaling particularly
when mixed-parameters cases are included, strongly
support the conclusion that Ipinch scaling is the more uni-
versal and robust one. Similarly conclusions on the im-
portance of Ipinch in plasma focus performance and scal-
ing laws have been reported [11–15].
Figure 6. Ysxr is plotted as a function of Ipinch and Ipeak. The
parameters kept constant for the black data points are:
RESF = 0.1, c = 1.5, L0 = 30nH and V0 = 20 kV and model
parameters fm, fc, fmr, fcr at 0.06, 0.7, 0.16 and 0.7 respec-
tively. The unblackened data points are for specific ma-
chines which have different values for the parameters c, L0,
V0 and RESF
It may also be worthy of note that our comprehen-
sively surveyed numerical experiments for Mather con-
figurations in the range of energies 0.2 kJ to 1 MJ pro-
duce an Ipinch scaling rule for Y
sxr not compatible with
Gates’ rule [37]. However it is remarkable that our Ipinch
scaling index of 3.6, obtained through a set of compre-
hensive numerical experiments over a range of energies
0.2 kJ to 1 MJ, on Mather-type devices is within the
range of 3.5to4 postulated on the basis of sparse experi-
mental data, (basically just two machines one at 5 kJ and
the other at 0.9 MJ), by Filippov [6], for Filippov con-
figurations in the range of energies 5 kJ to 1 MJ.
It must be pointed out that the results represent scaling
for comparison with baseline plasma focus devices that
have been optimized in terms of electrode dimensions. It
must also be emphasized that the scaling with Ipinch works
well even when there are some variations in the actual
device from L0 = 30 nH, V0 = 20 kV and c = 1.5. How-
ever there may be many other parameters which can
change and could lead to a further enhancement of x-ray
yield.
4. Conclusions
Numerical experiments carried out using the universal
plasma focus laboratory facility based on the Lee model
code gives reliable scaling laws for neutrons production
and neon SXR yields for plasma focus machines. The
scaling laws obtained:
For neutron yield:
Yn = 3.2x1011 Ipinch
4.5; Yn = 1.8x1010 Ipeak 3.8; Ipeak (0.3 to
5.7), Ipinch (0.2 to 2.4) in MA.
Yn~E0
2.0 at tens of kJ to Y
n~E0
0.84 at MJ level (up to
25MJ).
For neon soft x-rays:
Ysxr = 8.3x103 Ipinch
3.6; Ysxr = 6x102 Ipeak 3.2; Ipeak (0.1 to
2.4), Ipinch (0.07 to1.3) in MA.
Ysxr~E0
1.6 (kJ range) to Ysxr~E0 0.8 (towards MJ).
These laws provide useful references and facilitate the
understanding of present plasma focus machines. More
importantly, these scaling laws are also useful for design
considerations of new plasma focus machines particularly
if they are intended to operate as optimized neutron or
neon SXR sources. More recently, the scaling of Yn versus
E0 as shown above has been placed in the context of a
global scaling law [38] with the inclusion of available ex-
perimental data. From that analysis, the cause of scaling
deterioration for neutron yield versus energy as shown in
Figure 2 (which has also been given the misnomer ‘neu-
tron saturation’) has been uncovered as due to a current
scaling deterioration caused by an almost constant axial
phase ‘dynamic resistance’ interacting with a reducing
bank impedance as energy storage is increased at essen-
tially constant voltage. Solutions suggested include the use

S. H. SAW ET AL.
71
of ultra-high voltages and circuit enhancement techniques
such as current-steps [39,40]. It is suggested here that the
deterioration of soft x-ray yield with storage energy as
shown in Figure 5 could also be ascribed to the same axial
phase ‘dynamic resistance’ effect as described in that ref-
erence [38].
5. Acknowledgement
The authors acknowledge the contributions of Paul Lee
and Rajdeep Singh Rawat to various parts of this paper.
REFERENCES
[1] S. Lee, “Twelve years of UNU/ICTP PFF-A review,” IC/
98/231 Abdus Salam ICTP, Miramare, Trieste, pp. 5–34,
ICTP Open Access Archive, 1998, http://eprints.ictp.it/31/.
[2] Y. Kato and S. H. Be, Applied Physics Letters, No. 48, pp.
686, 1986
[3] E. P. Bogolyubov, V. D. Bochkov, V. A. Veretennikov, L.
T. Vekhoreva, V. A. Gribkov, A. V. Dubrovskii, P. Ivanov
Yu, A. I. Isakov, O. N. Krokhin, P. Lee, S. Lee, V. Ya Ni-
kulin, A. Serban, P. V. Silin, X. Feng, and G. X. Zhang,
“A powerful soft x-ray source for x-ray lithography based
on plasma focusing,” Physica Scripta, Vol. 57, pp. 488–
494, 1998.
[4] S. Lee, P. Lee, G. Zhang, X. Feng, V. A. Gribkov, L.
Mahe, A. Serban, and T. K. S. Wong, IEEE Transactions
on Plasma Science, No. 26, pp. 1119, 1998.
[5] N. V. Filippov, T. I. Filippova, M. A. Karakin, V. I. Krauz,
V. P. Tykshaev, V. P. Vinogradov, Y. P. Bakulin, V. V. Ti-
mofeev, V. F. Zinchenko, J. R. Brzosko, and J. S. Brzosko,
IEEE Transactions on Plasma Science, No. 24, pp. 1215–
1223, 1996.
[6] N. V. Filippov, T. I. Filippova, I. V. Khutoretskaia, V. V.
Mialton, and V. P. Vinogradov, “Megajoule scale plasma
focus as efficient X-ray source,” Physics Letters A, Vol.
211, No. 3, pp. 168–171, 1996.
[7] Institute for Plasma Focus Studies,
http://www.plasmafocus.net.
[8] Internet Workshop on Plasma Focus Numerical Experi-
ments (IPFS-IBC1), April 14–May 19, 2008,
http://www.plasmafocus.net/IPFS/Papers/IWPCAkeynote
2ResultsofInternet-basedWorkshop.doc.
[9] S. Lee, “Radiative dense plasma focus computation
package: RADPF,”
http://www.intimal.edu.my/school/fas/UFLF/File1RADPF.htm,
http://www.plasmafocus.net/IPFS/modelpackage/File1RA
DPF.htm.
[10] S. Lee, R. S. Rawat, P. Lee, and S. H. Saw, “Soft x-ray
yield from NX2 plasma focus-correlation with plasma
pinch parameters,” (to be published).
[11] S. Lee and S. H. Saw, “Neutron scaling laws from nu-
merical experiments,” Journal of Fusion Energy, No. 27,
pp. 292–295, 2008.
[12] S. Lee, “Current and neutron scaling for megajoule
plasma focus machine,” Plasma Physics and Controlled
Fusion, No. 50, 105005, (14pp), 2008.
[13] S. Lee, S. H. Saw, P. C. K. Lee, R. S. Rawat, and H.
Schmidt, “Computing plasma focus pinch current from
total current measurement,” Applied Physics Letters, No.
92, 111501, 2008.
[14] S. Lee and S. H. Saw, “Pinch current limitation effect in
plasma focus,” Applied Physics Letters, No. 92, 021503,
2008.
[15] S. Lee, P. Lee, S. H. Saw, and Rawat R S, “Numerical
experiments on plasma focus pinch current limitation,”
Plasma Physics and Controlled Fusion, No. 50, 065012
(8pp), 2008.
[16] S. Lee, “Plasma focus model yielding trajectory and
structure” in Radiations in Plasmas, B. McNamara, ed.,
World Scientific Publishing Co, Singapore, ISBN 9971-
966-37-9, Vol. 2, pp. 978–987, 1984.
[17] S. Lee, et al, “A simple facility for the teaching of plasma
dynamics and plasma nuclear fusion,” American Journal
of Physics, No. 56, pp. 62–68, 1988.
[18] T. Y. Tou, S. Lee, and K. H. Kwek, “Non perturbing
plasma focus measurements in the run-down phase,”
IEEE Transactions on Plasma Science, No. 17, pp. 311–
315, 1989.
[19] S. Lee, “A sequential plasma focus,” IEEE Transactions
on Plasma Science, Vol. 19, No. 12, pp. 912–919, 1991.
[20] J. B. Ali, “Development and studies of a small Plasma
focus,” PhD thesis, Universiti Teknologi Malaysia, Ma-
laysia, 1990.
[21] D. E. Potter, “The formation of high density z-pinches,”
Nuclear Fusion, Vol. 18, pp. 813–823, 1978.
[22] S. Lee and A. Serban, “Dimensions and lifetime of the
plasma focus pinch,” IEEE Transactions on Plasma Sci-
ence, Vol. 24, No. 3, pp. 1101–1105, 1996.
[23] M. H. Liu, “Soft X-rays from compact plasma focus,”
PhD thesis, NIE, Nanyang Technological University,
Singapore, 2006, ICTP Open Access Archive:
http://eprints.ictp.it/327/.
[24] S. Bing, “Plasma dynamics and x-ray emission of the
plasma focus,” PhD Thesis, NIE, Nanyang Technological
University, Singapore, 2000, ICTP Open Access Archive:
http://eprints.ictp.it/99/.
[25] A. Serban and S. Lee, “Experiments on speed-enhanced
neutron yield from a small plasma focus,” Journal of
Plasma Physics, Vol. 60, Part 1, pp. 3–15, 1998.
[26] M. H. Liu, X. P. Feng, S. V. Springham, and S. Lee, “Soft
x-ray measurement in a small plasma focus operated in
neon,” IEEE Transactions on Plasma Science, No. 26, pp.
135–140, 1998.
[27] D. Wong, P. Lee, T. Zhang, A. Patran, T. L. Tan, R. S.
Rawat, and S. Lee, “An improved radiative plasma focus
model calibrated for neon-filled NX2 using a tapered an-
ode,” Plasma Sources Science and Technology, No. 16,
pp. 116–123, 2007.
[28] S. Lee, 2000–2007, http://ckplee.myplace.nie.edu.sg/plas-

S. H. SAW ET AL.
72
maphysics/.
[29] S. Lee, 2005, ICTP Open Access Archive: http://eprints.
ictp.it/85/.
[30] M. A. Mohammadi, S. Sobhanian, C. S. Wong, S. Lee, P.
Lee, and R. S. Rawat, “The effect of anode shape on neon
soft x-ray emissions and current sheath configuration in
plasma focus device,” Journal of Physics D: Applied
Physics, 42, 2009, 045203 (10pp).
[31] Springham S V, Lee S and Rafique M S, “Correlated
deuteron energy spectra and neutron yield for a 3 kJ
plasma focus,” Plasma Physics Controlled Fusion, Vol. 42,
pp. 1023–1032, 2000.
[32] S. Lee, P. Lee, G. Zhang, X. Feng, V. A. Gribkov, M. Liu,
A. Serban, and T. Wong “High rep rate high performance
plasma focus as a powerful radiation source,” IEEE
Transactions on Plasma Science, Vol. 26, No. 4, pp. 1119–
1126, 1998.
[33] V. Siahpoush, M. A. Tafreshi, S. Sobhanian, and S. Khor-
ram, “Adaptation of Sing Lee’s model to the Filippov
type plasma focus geometry,” Plasma Physics Controlled
Fusion, No. 47, pp. 1065–1072, 2005.
[34] V. A. Gribkov, A. Banaszak, B. Bienkowska, A. V. Du-
brovsky, I. Ivanova-Stanik, L. Jakubowski, L. Karpinski,
R. A. Miklaszewski, M. Paduch, M. J. Sadowski, M.
Scholz, A. Szydlowski, and K. Tomaszewski, “Plasma
dynamics in the PF-1000 device under full-scale energy
storage: II, Fast electron and ion characteristics versus
neutron emission parameters and gun optimization per-
spectives,” Journal of Physics D: Applied Physics, No. 40,
pp. 3592–3607, 2007.
[35] J. D. Huba, Plasma Formulary page, No. 44, 2006.
[36] S. Lee, S. H. Saw, P. Lee, and R. S. Rawat, “Numerical
experiments on plasma focus neon soft x-ray scaling,”
Plasma Physics and Controlled Fusion, No. 51, 105013
(8pp), 2009,
Available at http://stacks.iop.org/PPCF/51/105013.
[37] D. C. Gates, Proceedings of the 2nd International Con-
ference on Energy Storage, Compression and Switching,
Venice, No. 2, pp. 3239, Plenum Press, New York, 1983.
[38] S. Lee, “Neutron yield saturation in plasma focus-A
fundamental cause,” Applied Physics Letters, No. 95,
151503, First online 15 October 2009.
[39] S. H. Saw, “Experimental studies of a current-stepped
pinch,” PhD Thesis Universiti Malaya, Malaysia, 1991.
[40] S. Lee, “A current-stepping technique to enhance pinch
compression,” Journal of Physics D: Applied Physics, No.
17, pp. 733–739, 1984.