Energy and Power Engineering, 2010, 39-45
doi:10.4236/epe.2010.21007 Published Online February 2010 (http://www.scirp.org/journal/epe)
Simulation of Electric Fields in Small Size
Divertor Tokamak Plasma Edge
A. H. BEKHEIT
Plasma & Nuclear Fusion Department, Nuclear Research Centre, Atomic Energy Authority, Cairo, Egypt
Abstract: The fluid simulation of Small Size Divertor Tokamak (SSDT) plasma edge by the B2-SOLPS5.0
2D [1] transport code gives the following results: First, in the vicinity of separatrix the radial electric field
result is not close to the neoclassical electric f ield. Second, the shear of radial electric f ield is independent on
plasma parameters. Third, switching on poloidal dr ifts (E×B and diamagnetic drifts) leads to asymmetric par-
allel and poloidal fluxes from outer to inner plates and upper part of SOL for normal direction of toroidal
magnetic field. Fourth, for the normal direction of toroidal magnetic, the radial electric field of SSDT is af-
fected by the variation in temperature heating of plasma. Fifth, the parallel flux is directed from inner to outer
plate in case of discharge without neutral beam injection (NBI).
Keywords: electric field, transport codes, divertor tokamak
1. Introduction
A regime of improved confinement is extremely impor-
tant for the operation of a thermonuclear reactor. A tran-
sition from the low confinement (L-mode) to high con-
finement regime (H-mode) was discovered [2], and since
then it has been observed on many tokamaks and stel-
larators. The L-H transition may be caused by a strong
radial electric field at the edge plasma and suppression of
the fluctuation level by strong poloidal rotation in the
EB fields [3,4]. As a result, the transport coefficients
are strongly reduced in the H-mode and transport barriers
with steep density and temperature gradients were
formed near the separatrix or close flux surface. The key
element in the transition physics is the origin of the
strong radial electric field in the edge plasma. If the ra-
dial electric field is sufficiently strong, the poloidal EB
flow acquires a large shear, which is considered to be
necessary for suppression of edge turbulence. The radial
electric field in the separatrix vicinity is simulated by
using the B2-SOLPS5.0 two dimensional fluid code [1],
in which most complete system of transport equations is
solved including all the important perpendicular current
and EB drifts for SSDT. This code differs from the
similar fluid codes (e.g. codes [5,6]), since it included
detail account of parallel viscosity and perpendicular
current. The equation system provides a transition to the
neoclassical equation when the anomalous transport co-
efficients are replaced by classical value. The simulation
is performed for SSDT, where the plasma parameters in
the separatrix vicinity and the Scrap Off Layer (SOL)
correspond to Pfirch-Schlueter regime [7], thus justifying
the applicability of the fluid equations. On the basis of
simulation for different power of additional heating,
plasma densities, toroidal rotation velocities and mag-
netic field directions, it is demonstrated that the radial
electric field in the separatrix vicinity is not of the order
of the neoclassical field. In this paper the shear of the
poloidal EB drifts is calculated. It is shown that the
shear of the poloidal rotation is not function of plasma
parameters.
2. Simultion Results
The computation region for simulation is based on Single
Null (SN) magnetic divertor and covers the SOL, core
and private regions as shown in Figure 1. In computation
region the coordinate which vary in the direction along
flux surfaces (x-coordinate or poloidal coordinate) and
the coordinate which vary in the direction across flux
surfaces (y-coordinate or radial coordinate). The compu-
tation mesh is divided into 24×96 units (where-1 x  96,
-1  y 24) and the separatrix was at y=12. The simula-
tions were performed for L-regimes of SSDT (minor
radius a=0.1m, major radius R=0.3 m, I=50kA, BT=1.7 T,
electron density at equatorial midplane ne =ni =n =2 
1019 m-3, ion temperature Ti=31-93 eV).
The anomalous values of diffusion and heat conduc-
tivity coefficients were chosen: D=0.5 m2s-1, 
e,i = 0.7
m2s-1. The perpendicular viscosity was taken in the
form  =nmiD. The inner boundary flux surface, was
located in the core few cm from the separetrix, the
boundary conditions for the density of plasma, the av-
erage toroidal momentum flux, the electron and ion

A. H. BEKHEIT
40
Figure 1. Coordinate system and simulation mesh
0510 15 20 25
-2
-1
0
1
2
3
4
5
6
Separatrix
Er ( K V / m2 )
y (cm )
C o de
Ne o c la s s ic a l
Figure 2. Radial electric field at edge of SSDT for discharge
without neutral beam injection (NBI) at Ti = 31 e v, ni =
41019m-3
heat fluxes were specified [8]. The first result of simula-
tions for the radial electric field Er was compared with the
neoclassic al el ect ric fiel d E (NEO) which is given by [7]:


 dxg
dxBVg
b
dy
Td
h
k
dy
nd
he
T
Ex
i
y
T
y
i
NEO || )( )
ln1ln1
(
(1)
where bx= Bx/B (Bx is poloidal magnetic field and
22
x
z
BBB where Bz is toroidal magnetic fields),
x
yz
g
hhh is the metric coefficients, (hx = 1/ x, hy
= 1/ y, hz = 1/ z) V is the parallel (toroidal) ve-
locity (the coefficient kT = 2.7 corresponds to the
Pfirsch-Schlueter regime).Typical radial electric field is
shown in Figure 2. The comparison is showed that in the
vicinity of separatrix the radial electric field is not order
of the neoclassical electric field for both discharges
without neutral beam injection (NBI). This fact means
that, the radial transport of toroidal (parallel) momentu m
is larger than parallel viscosity in parallel momentum
balance equation [8]. It is worth to mention that the av-
eraged parallel velocity in Equation (1) is determined by
the radial transport of parallel (toroidal) momentum i.e.
by anomalous values of the diffusion and perpen-dicular
viscosity coefficients. The radial profiles of parallel ve-
locity for different values of averag e velocity at the inn er
boundary are shown in Figure 3. Even in the Ohmic case
the contribution from the last term in Equation (1) is not
negligible and should take into account. The second re-
sult, the radial electric field calculate by the code is
negative in core, vicinity of separatrix and is positive in
SOL, Figures 2. For normal direction of toroidal mag-
netic field in SOL one can see that the Er  BT drifts are
directed from outer plate to inner plate in SOL, and from
inner plate to outer plate in the private region as shown
0510 15 20 25
-50000
-40000
-30000
-20000
-10000
0
10000
20000
30000
40000
50000
Core SOL
separatrix
Vll ( m /sec)
y
b(N o N BI)
b(Co-injection )
b(Contra-injection)
Figure 3. Parallel velocity for discharges with co and contra-
injection neutral beam (NBI), for parameter of SSDT
Figure 4. The arrows shows the direction of E × B drifts in
the edge plasma of small size divertor tokamak
Inner plate
SOL Core
Outer plate
Private re gio n
Separatrix
x
y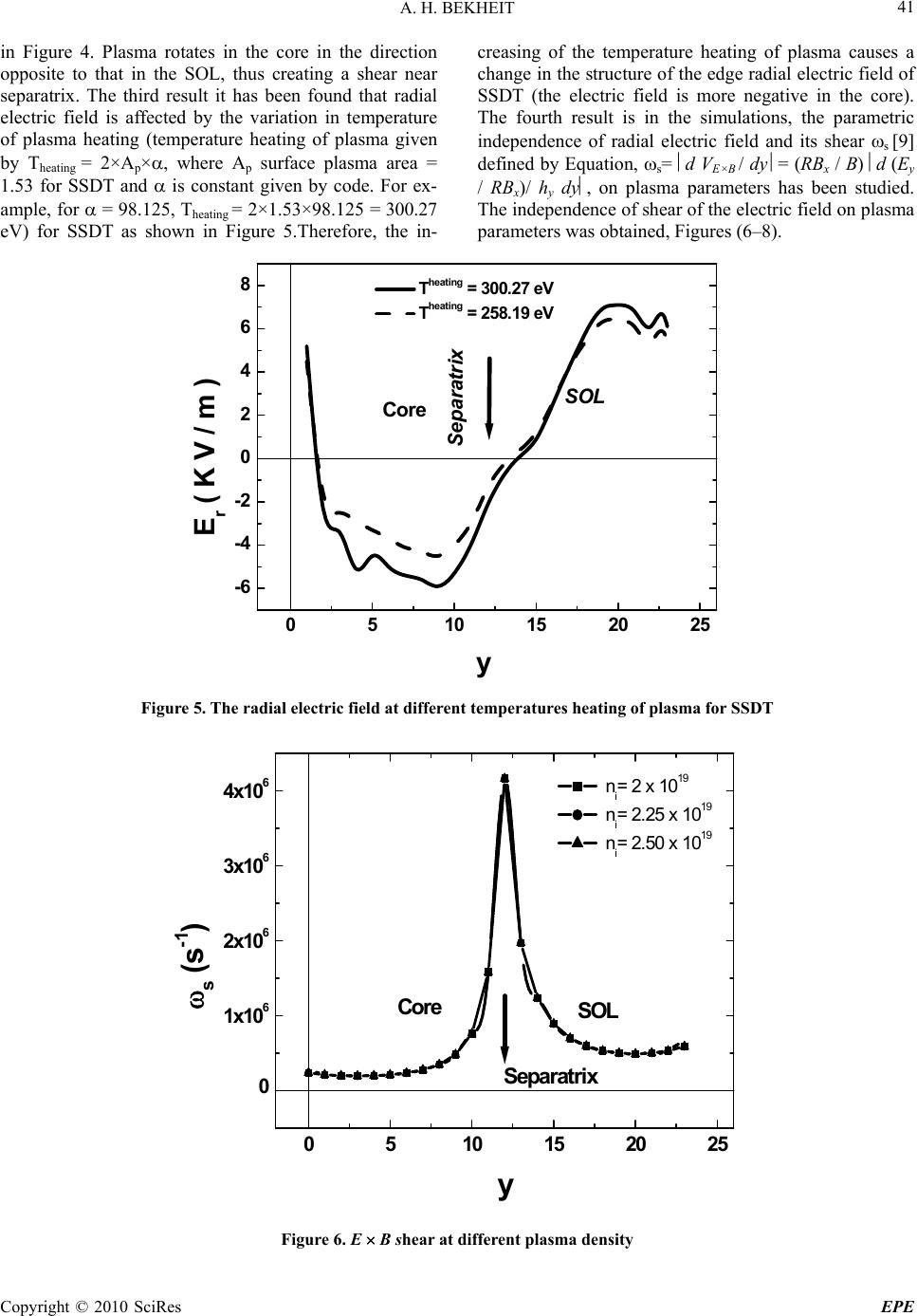

A. H. BEKHEIT
41
in Figure 4. Plasma rotates in the core in the direction
opposite to that in the SOL, thus creating a shear near
separatrix. The third result it has been found that radial
electric field is affected by the variation in temperature
of plasma heating (temperature heating of plasma given
by Theating = 2×Ap×, where Ap surface plasma area =
1.53 for SSDT and  is constant given by code. For ex-
ample, for  = 98.1 25, Theating = 2×1.53×98.125 = 300.27
eV) for SSDT as shown in Figure 5.Therefore, the in-
creasing of the temperature heating of plasma causes a
change in the structure of the edge radial electric field of
SSDT (the electric field is more negative in the core).
The fourth result is in the simulations, the parametric
independence of radial electric field and its shear s [9]
defined by Equation, s= d VE×B / dy = (RBx / B) d (Ey
/ RBx)/ hy dy, on plasma parameters has been studied.
The independence of shear of the electric field on plasma
parameters was obtained, Figures (6–8).
0510 1520 25
-6
-4
-2
0
2
4
6
8
Core SOL
Separatrix
Er ( K V / m )
y
Theat ing = 300.27 eV
Theat ing = 258.19 eV
Figure 5. The radial electric field at different temperatures heating of plasma for SSDT
0510 15 20 25
0
1x106
2x106
3x106
4x106
Core SOL
Separatrix
s (s-1)
y
ni= 2 x 1019
ni= 2.25 x 1019
ni= 2.50 x 1019
Figure 6. E  B shear at different plasma density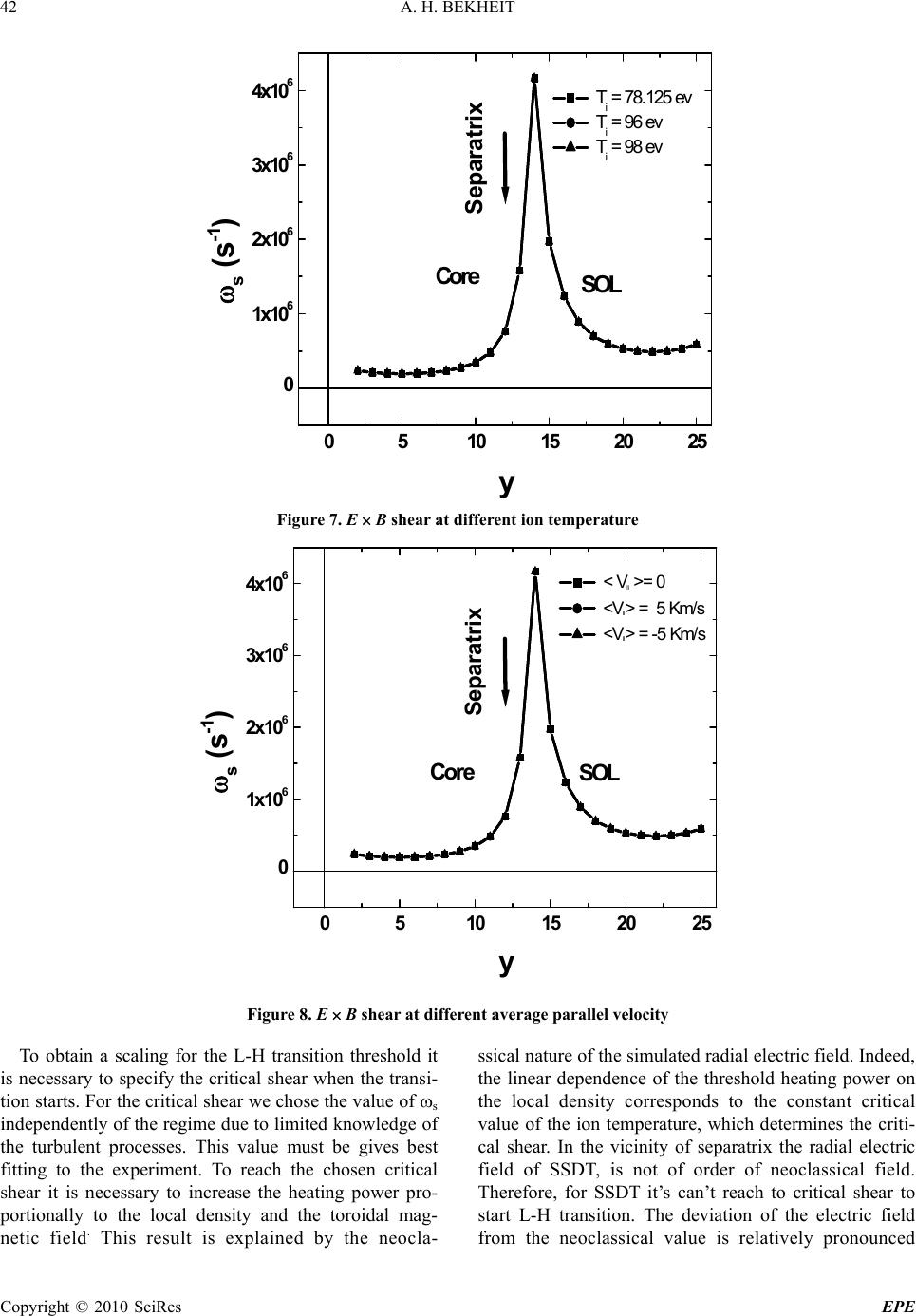

A. H. BEKHEIT
42
0510 15 20 25
0
1x106
2x106
3x106
4x106
CoreSOL
Separat rix
s (s -1)
y
T i = 78.125 ev
T i = 96 ev
T i = 98 ev
Figure 7. E  B shear at different ion temperature
051015 20 25
0
1x106
2x106
3x106
4x106
CoreSOL
Sep ara trix
s (s-1)
y
< V ll >= 0
< V ll> = 5 K m/s
< V ll> = -5 K m/s
Figure 8. E  B shear at different average parallel velocity
To obtain a scaling for the L-H transition threshold it
is necessary to specify the critical shear when the transi-
tion starts. For the critical shear we chose the value of s
independently of the regime due to limited knowledge of
the turbulent processes. This value must be gives best
fitting to the experiment. To reach the chosen critical
shear it is necessary to increase the heating power pro-
portionally to the local density and the toroidal mag-
netic field. This result is explained by the neocla-
ssical nature of the simulated radial electric field. Indeed,
the linear dependence of the threshold heating power on
the local density corresponds to the constant critical
value of the ion temperature, which determines the criti-
cal shear. In the vicinity of separatrix the radial electric
field of SSDT, is not of order of neoclassical field.
Therefore, for SSDT it’s can’t reach to critical shear to
start L-H transition. The deviation of the electric field
from the neoclassical value is relatively pronounced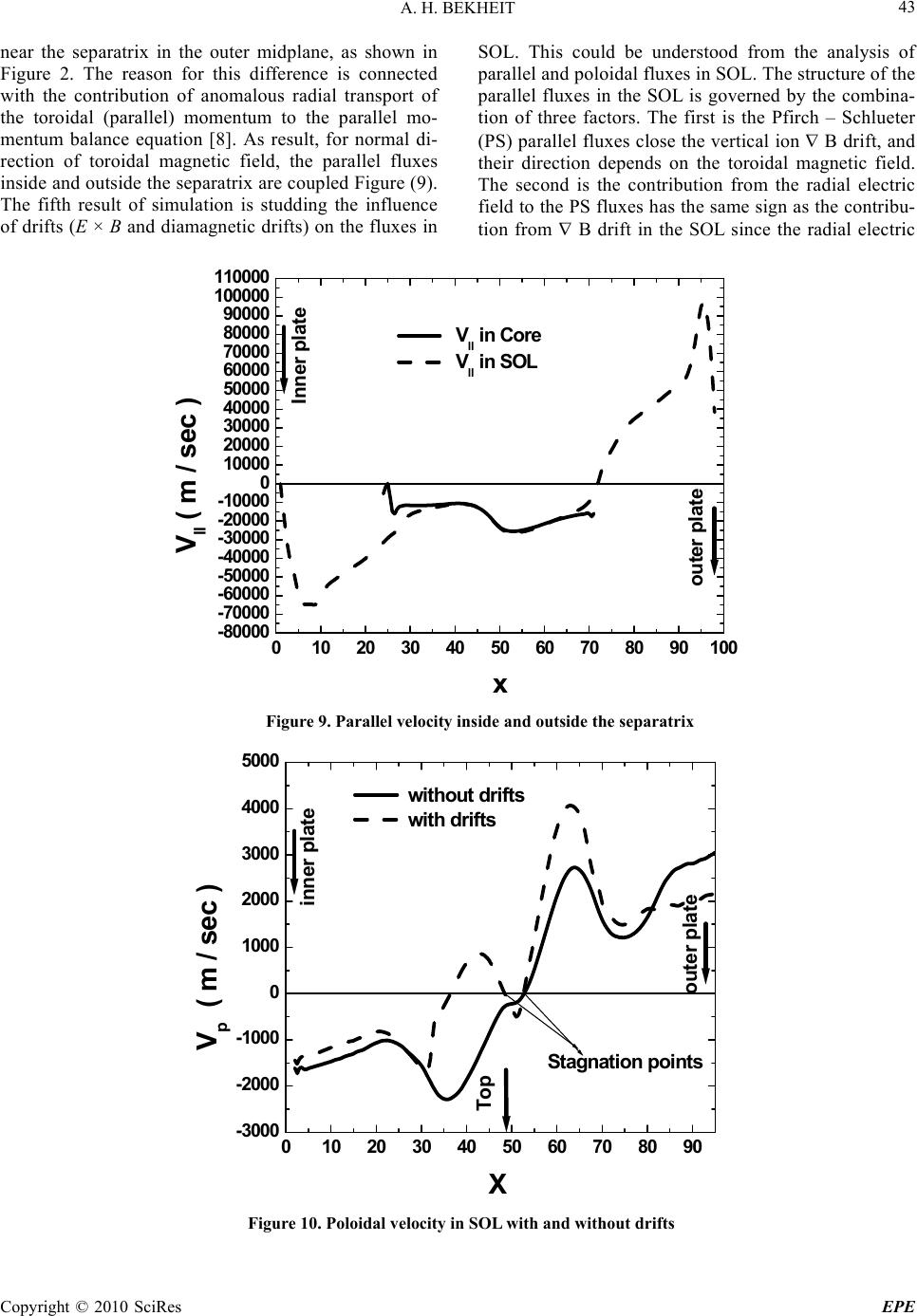

A. H. BEKHEIT
43
near the separatrix in the outer midplane, as shown in
Figure 2. The reason for this difference is connected
with the contribution of anomalous radial transport of
the toroidal (parallel) momentum to the parallel mo-
mentum balance equation [8]. As result, for normal di-
rection of toroidal magnetic field, the parallel fluxes
inside and outside the separatrix are coupled Figure (9).
The fifth result of simulation is studding the influence
of drifts (E × B and diamagnetic drifts) on the fluxes in
SOL. This could be understood from the analysis of
parallel and poloidal fluxes in SOL. The structure of the
parallel fluxes in the SOL is governed by the combina-
tion of three factors. The first is the Pfirch – Schlueter
(PS) parallel fluxes close the vertical ion  B dr ift, and
their direction depends on the toroidal magnetic field.
The second is the contribution from the radial electric
field to the PS fluxes has the same sign as the contribu-
tion from  B drift in the SOL since the radial electric
0 102030405060708090100
-80000
-70000
-60000
-50000
-40000
-30000
-20000
-10000
0
10000
20000
30000
40000
50000
60000
70000
80000
90000
100000
110000
outer p late
Inner plate
Vll ( m / sec )
x
Vll in Co r e
Vll in SOL
Figure 9. Parallel velocity inside and outside the separatrix
0 102030405060708090
-3000
-2000
-1000
0
1000
2000
3000
4000
5000
Stagnation points
Top
outer plate
inner plate
Vp ( m / se c )
X
without drifts
w ith d rift s
Figure 10. Poloidal velocity in SOL with and without drifts

A. H. BEKHEIT
44
0 102030405060708090100
-160000
-140000
-120000
-100000
-80000
-60000
-40000
-20000
0
20000
40000
60000
80000
100000
120000
140000
160000
Top
stagnation point
stagnation point
outer plate
inner plate
Vll ( m / sec )
x
w ith d r ifts
w ith o u t d r ifts
Figure 11. Parallel velocity with and without drifts
051015 2025
-20000
-18000
-16000
-14000
-12000
-10000
-8000
-6000
-4000
-2000
Core SOL
Separatrix
Vll ( m / sec )
y ( cm )
Figure 12. Parallel flux in the edge of SSDT
field is positive in the SOL as shown in Figure 2 (inside
separatrix, where the radial electric field is negative, the
contribution to PS fluxes  B drifts and EB drift
compensate each other in accordance with neoclassical
theory). The third contribution arises from the poloidal
fluxes that are responsible for the particle transport to the
plates. Those poloidal fluxes are closed the radial diffu-
sive particle fluxes. In the absence of the poloidal EB
and  B drifts these fluxes coincide with the projection
of the parallel fluxes. On the one hand, the outer plate is
larger than the inner plate and the integral poloidal flux
to this plate should be larger. On the other hand, since the
plasma in the vicinity of the inner plate is colder and
denser, the particle flux per square meter to this plate that
is proportional to n (T/mi)1/2 is larger than particle flux to
outer plate (the pressure is almost the same at the plates).
Switching on EB drift leads to asymmetric in parallel
and poloidal fluxes from outer to inner plates and upper
part of SOL as shown as in Fig ures (10,11). Also switch-
ing on the poloidal dr ifts leads to decrease of the parallel
velocity, because the poloidal projection of the parallel
velocity not compensates poloid al EB drifts, so that the
poloidal rotation changes. Moreover, the position stagna-
tion point for the poloidal did not change much which is

A. H. BEKHEIT
45
located somewhere near the upper part of the SOL, as
shown in Figure 11. In contrast, the position of the stag-
nation point for parallel flux may be significantly differ-
ent Figure 11. For normal B the stagnation point is
strongly shifted toward s the outer plate. This fact is con-
sistent with the observations with simulations [10]. Fi-
nally the parallel flow pattern is the result of all three
factors. For normal B parallel flux in SOL is negative as
sh own in Fig ure 12. Therefo re, for normal B parallel flux
is directed from outer to inner plate.
3. Conclusions
In conclusion, the performed simulations for SSDT
demonstrate the following results: (First) In the vicinity
of separatrix the radial electric field was not close to the
neoclassical electric field. (Second) the independence of
the shear of radial electric field on plasma parameters.
(Third) For normal direction of torodial magnetic field,
the radial electric field of SSDT was affected by the
variation in temperature heating of plasma. (Fourth)
Switching on poloidal d rifts leads to asymmetric parallel
and poloidal fluxes from outer to inner plates and upper
part of SOL for normal direction of toroidal magnetic
field. Also switching on the poloidal drifts leads to de-
crease of the parallel velocity, because the poloidal pro-
jection of the parallel velocity not compensates poloidal
EB drifts, so that the poloidal rotation changes. (Fifth)
The parallel flux is directed from outer to inner plate.
(Sixth) The E×B drift are directed from outer plate to
inner plate in SOL, and from inner plate to outer plate in
the private region.
REFERENCES
[1] R. Schneider, V. Rozhansky, and P. Xantopoulos, Contri-
bution Plasma Physics, No. 40, pp. 4213, 2004.
[2] F. Wagner, Physical Review Letters, No. 49, pp. 1408,
1982.
[3] H. Biglari, P. H. Diamond, and P. W. Terry, Physics of
Fluids, No. B21, pp. 1, 1990.
[4] K. H. Burrell, Physics of Plasma, No. 4, pp. 1499, 1997.
[5] G. J. Radford, Contribution Plasma Physics, No. 36, pp.
187, 1996.
[6] T. D. Rognlien, D. D. Ryutov, N. Mattor, and G. D. Porter,
Physics of Plasmas, No. 6, pp. 1851, 1999.
[7] S. P. Hirshman and D. J. Sigmar, Nuclear Fusion, No. 21,
pp. 1079, 1981.
[8] A. H. Bekheit, Egyptian Journal of Fusion energy, Vol. 28,
No. 4, pp. 338–345, 2008.
[9] T. S. Hahm and K. H. Burrell, Phyics of Plasma, No. 2,
pp. 1648, 1994.
[10] S. K. Erents, G. Corrigan, and J. Spence, Journal of Nu-
clear Materials, No. 290–293, pp. 518, 2001.