Natural Science
Vol.4 No.8A(2012), Article ID:21657,5 pages DOI:10.4236/ns.2012.428091
Seismic response of high-rise steel framed buildings with Chevron-braced designed according to Venezuelan codes
![]()
1Structural Engineering Department, School of Civil Engineering, Lisandro Alvarado University, Barquisimeto, Venezuela; *Corresponding Author: rugel@ucla.edu.ve, ronald.david.ugel@upc.edu
2Technical University of Catalonia, Barcelona, Spain
Received 31 May 2012; revised 28 June 2012; accepted 12 July 2012
Keywords: Framed Steel Buildings; Chevron Braced Frames; Non Linear Analysis; Over Strength; Seismic Response
ABSTRACT
The object of this study is to determine the seismic response of regular high-rise steel buildings with Chevron-braced frames. Mechanics models of three buildings of 14, 18 and 20 stories are studied, all of them with similar geometric characteristics in plan and elevation. These models are realized using prescriptions and parameters from Venezuelan design codes. The seismic action is carried out through varius synthetic design spectrum compatible accelerograms defined by the seismic codes in this study, with three levels of intensity corresponding to three specific Limit States. Dynamic analysis is used to compute parameters of ductility, over strength and maximum displacements. From these results it can be concluded that Chevron-braced frames presented a good overall performance and non V-braced frames show greater damage due to dynamic actions, validating non linear dynamic analysis as a very powerful tool to seismic-resistance design and Chevron-braced frames as a very useful choice for improving the response of tall steel structures. Since this lateral bracing system is absent from Venezuelan seismic codes.
1. INTRODUCTION
At present, near of 80% of Venezuela people live in zones of high seismic hazard, Alonso [1]. Permanent studies on the behavior of structures before seismic events and the earthquake resistant design new buildings have lead to progressive improvement of the codes. For that it’s necessary to know as much as possible the probable behavior of structures under strong earthquakes, considering local and global conditions that may influence in the global behavior.
In framed steel structures it is very common the use of Chevron-braced frames as structural elements to provide additional stiffness, therefore reducing lateral displacements, Longo, Montuori and Piluso [2], but this system is under continued investigations to know its more efficient use and for codes optimization. Venezuelan norms [3-5] specify the minimum requirements for the design of steel structures and resistant earthquake design of buildings, but leave to the designer the election of the analysis method that adapts more to the characteristics of the structure.
Searching for a suitable configuration, the designer has the option to use methods or mathematical models able to reproduce the most realistic behavior of a structure before an earthquake, which is particularly important when structures are beyond the elastic range, Song and Ellingswood [6]. This detailed knowledge of the nonlinear response (constitutive and geometric) is necessary since the elastic analysis does not provide the necessary information for the determination of this behavior, Vielma, Barbat and Oller, [7]. By means of the nonlinear analysis it is possible to know the seismic behavior of structures under lateral forces generated by strong seismic events.
To describe in suitable form the behavior of the structural system throughout all the deformations range, it is necessary to adopt a structural idealization that includes the nonlinear behavior at constitutive and geometric level that vary with the deformation level reached, Dolsek [8]; the incorporation of synthetic elastic design spectrum compatible accelerograms based on seismic events previously registered, allows to know the displacements that the building can reach and to determine the collapse point, thus providing parameters that allow to evaluate accurately the design of the analyzed structure and to propose improvements in the earthquake resistant design of structures.
2. DESIGN OF CASES STUDIED
In order to carry on the nonlinear analysis of the seismic response in the studied structures, the mathematical model was determined to represent: 1) the structures; 2) the estimated loads and combinations applied on the structure; and 3) nonlinear pseudo static and dynamic analysis of the mechanical model of these structures. All the mathematical models have the same regular structural configuration in plant as in elevation, with concentric diagonals type V inverted in the outer frames in directions X and Y. Inter stories and roof slabs have secondary and bracing beams in Y direction and the load beams are placed in X direction (see Figure 1).
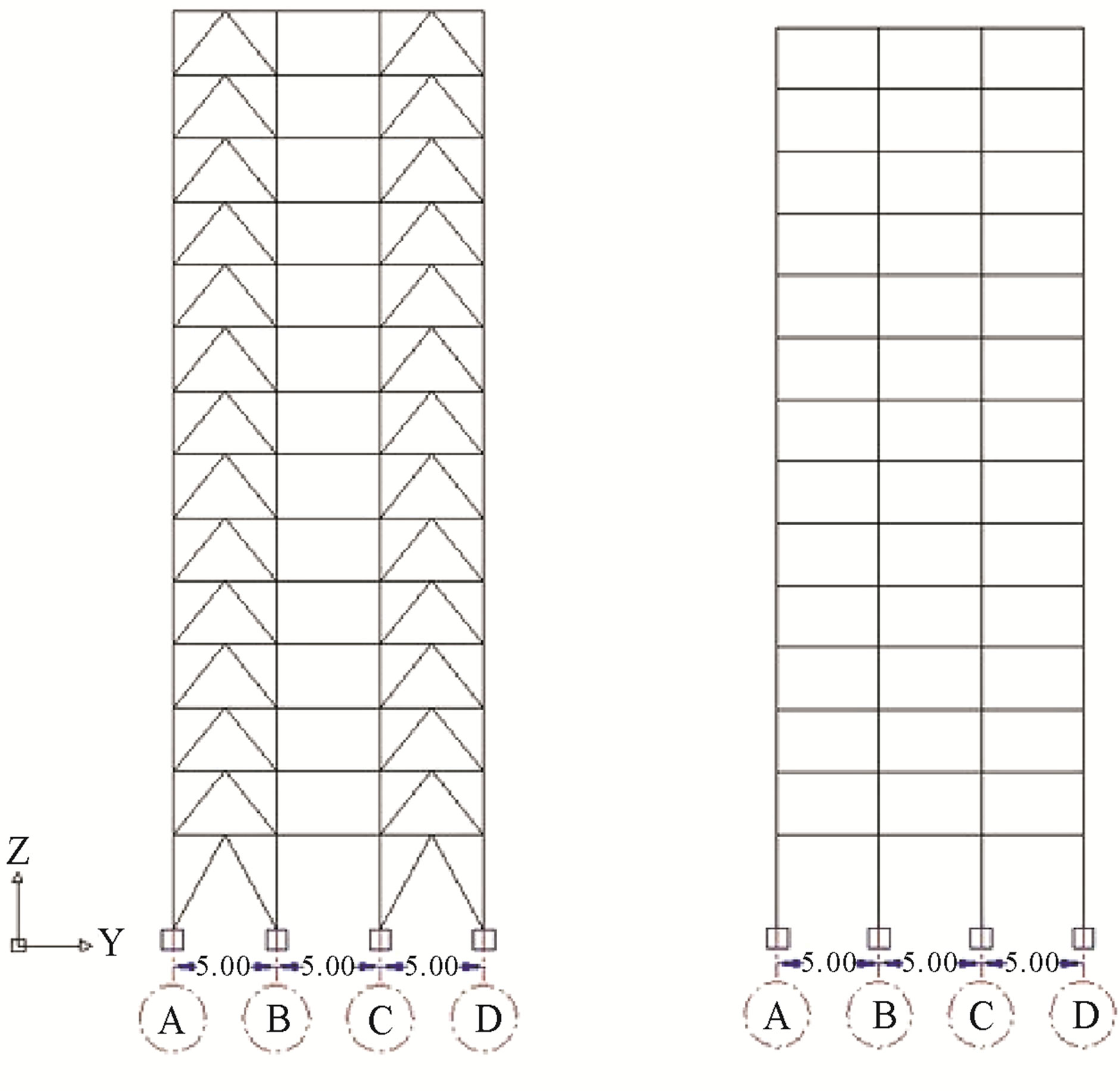
The X direction is composed of 3 spans of 6.00 m each; Y direction is made up of 3 spans of 5.00 m each, the elevation of the first story is 4.50 m and the rest of the stories have 3.00 m of elevation. Outer frames are Vbraced in external spans and inner frames have no bracing (see Figure 2). The three models differ only in the number of stories. The analysis performed in models and proposed structures includes the determination of a specific sectional area for each element of the structure.
2.1. Non Linear Analysis
The structure is modeled by incorporating the structural response when it incurred in the inelastic range of material produced by high deformations caused by accidental excitations (earthquakes), Vielma, Barbat and Oller, [9]. In non-linear dynamic analysis, input earthquakes are usually modeled using a time-history function, which implies a step-by-step evaluation of the response of the building. In this study, the inelastic analysis was carried out using the software Zeus NL, Elnashai, Papanicolau and Lee, [10]. Because of the symmetry and regularity of the proposed structures, two-dimensional
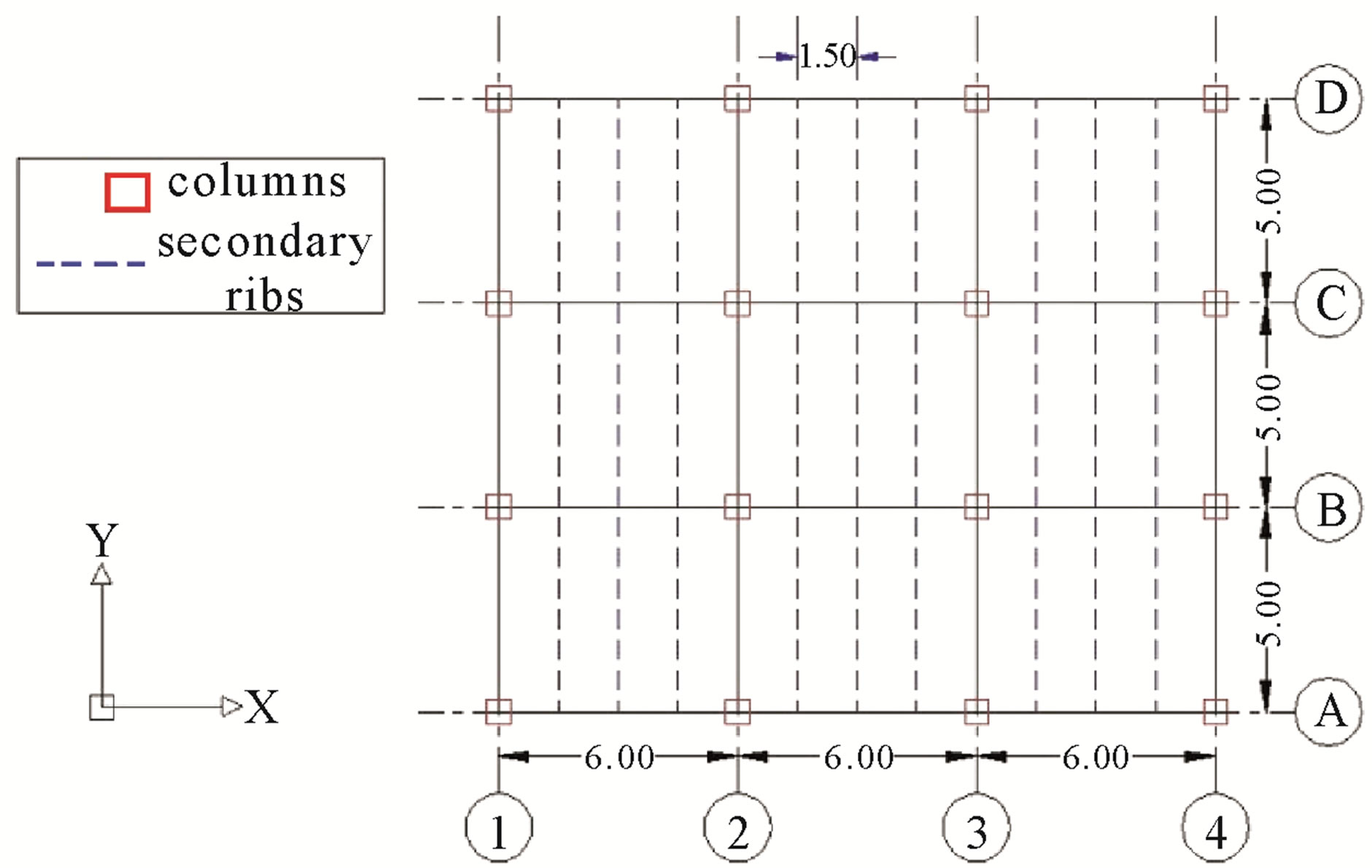
Figure 1. Typical plant of studied buildings.
 (a) (b)
(a) (b)
Figure 2. Elevation of 14 stories model. (a) Outer frames; (b) Inner frames.
analysis could be performed in four typical frames for each building (V-braced frame and non V-braced frame, both in the X direction and in the Y direction). Frame’s geometry was defined considering the material and the sections corresponding to each structural member. Every member was splitted in four elements according to the discretization that must be performed for the elements to determine those where the damage is concentrated during seismic action. Then, nodes are loaded by adding gravity forces obtained from elastic analysis. This analysis implies the realization of Pushover analysis, the determination of the structural ductility and the reserve of resistance.
2.2. Dynamic Analysis
Structures studied were subjected to three types of earthquakes of different magnitudes each one. Table 1 specifies the characteristics of the earthquakes that were used on the structures.
In the procedure, the accelerograms were introduced to each frame of the structures, then the results were used to compute the inter story drifts and global drifts as a function of time (t). There were simulated three (3) synthetic accelerograms generated with the program PACED, UCLA-CIMNE [11], from the elastic spectrum corresponding to the emplacement site design of the building stiff soil and differentiated one to another by their intensity and return period.
A frequent earthquake structure response allows to verify the Serviceability Limit State (SLS) through the inter story drifts. The pattern of comparison is governed by the requirements recommended by Di Sarno and Elnashai [12] which stipulate that these drifts should be under 0.5%. With the Rare earthquake, the Reparable damage Limit State (RDLS) is verified in function of inter story drifts which must not exceed 1.5% according to the same recommendations. For the Very Rare earthquake, the evaluation verify the Prevention of Collapse Limit State (PCLS), where the inter story drifts must be less than 3% to meet this requirement.
3. RESULTS ANALYSIS
The applied analysis provided the following results: For each frame is plotted 1) the capacity curve representing the values of base shear versus roof displacement. From this curve it is obtained the over strength; 2) the idealized capacity curve represented by the base shear in function of displacement, obtaining the ductility and identifying the yielding point. These standardized curves shows that V-braced frames require greater lateral forces towards the ultimate point, presenting a difference of 60% between V-braced and non V-braced frames. Table 2 presents the values of ductility and over strength from the idealized and real curves in the 14 story building. Figure 3 presents an idealized 14 story building capacity curve. From over strength, ductility and considering factors associated with structural redundancy it was obtained a response reduction factor (R) exceeding the value R = 6 considered in the design.
Dynamic Analysis
The global drift gives an approximate idea of damage level and structural behavior before a seismic event. For each earthquake it was obtained global drifts for each one of the frames. The 80 seconds in duration earthquake was the most severe on maximum drift. In almost all
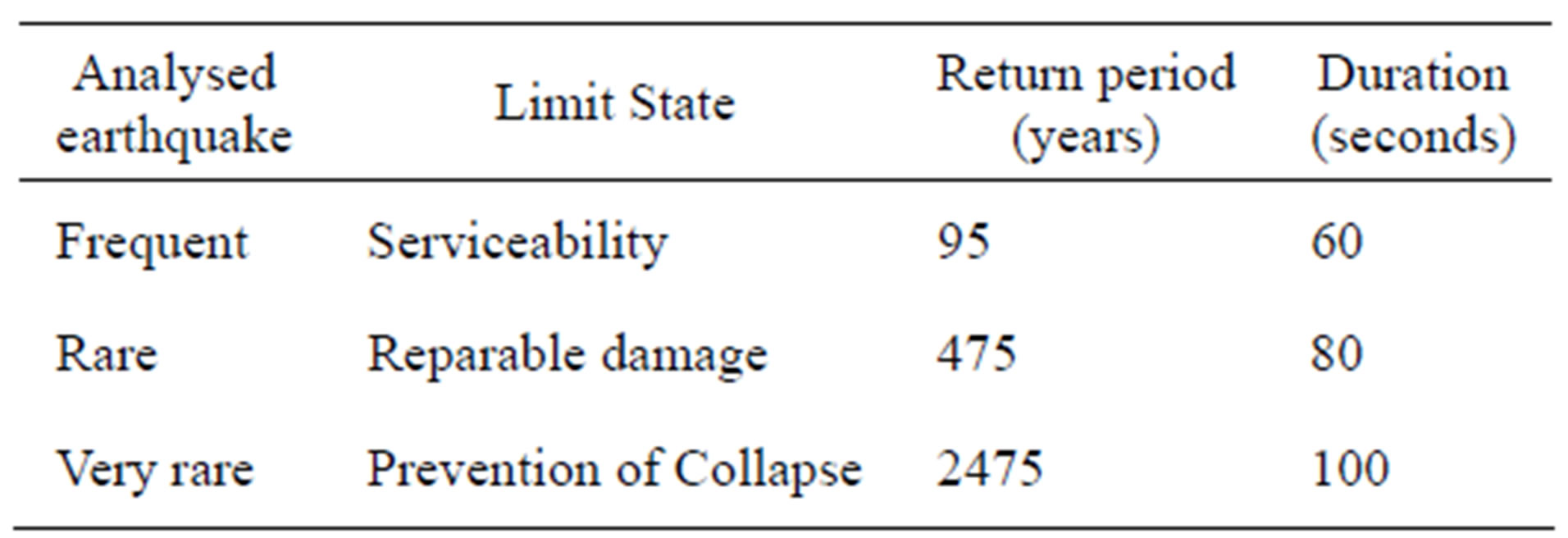
Table 1. Utilized earthquakes description.
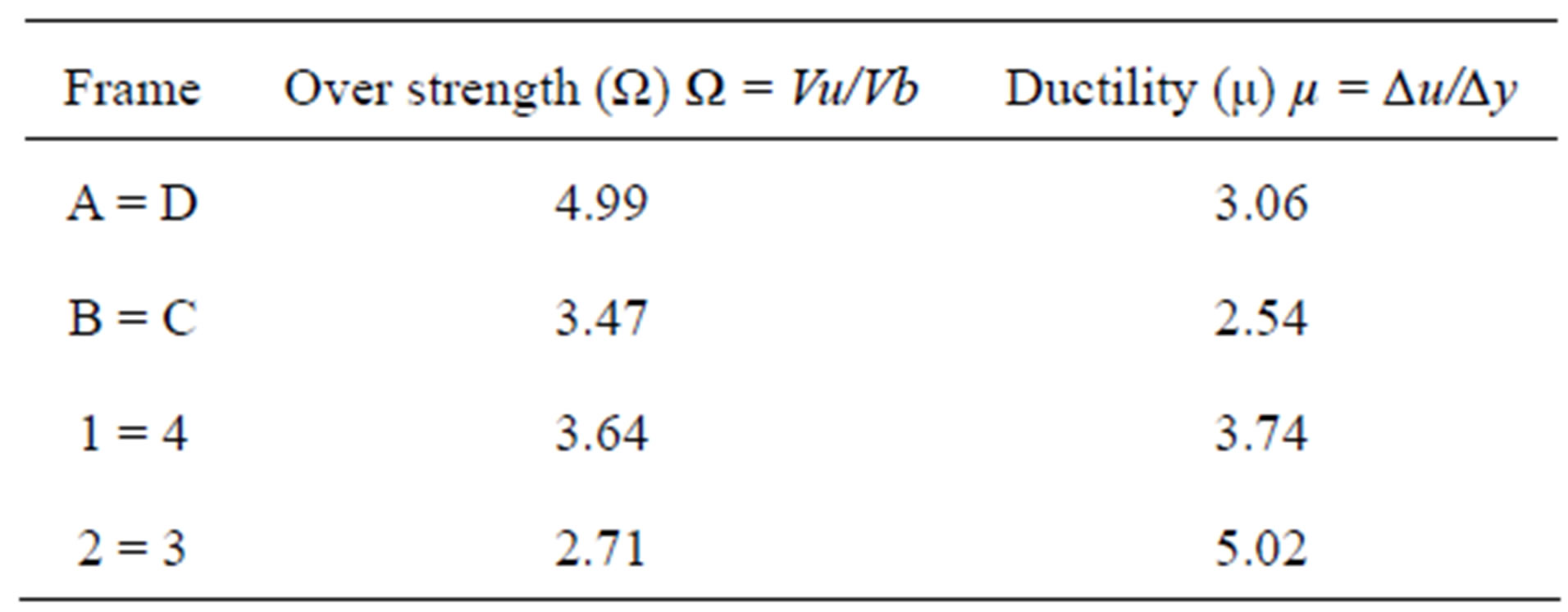
Table 2. Over strength and ductility for 14 story model.
frames of the buildings, the interstory drift exceed the maximum limit value of 0.5% considered in this study for the action of a frequent earthquake (50% in 50 years). Otherwise occurred to the rare earthquake (10% in 50 years) and very rare earthquake (2% in 50 years), where the limit of 1.5% and 3% values were not exceeded. The global drifts curves in function of time obtained for the frames are shown in Figures 4-6.
Percentage displacement versus time for each considered earthquake was generated for interstory drifts. Only
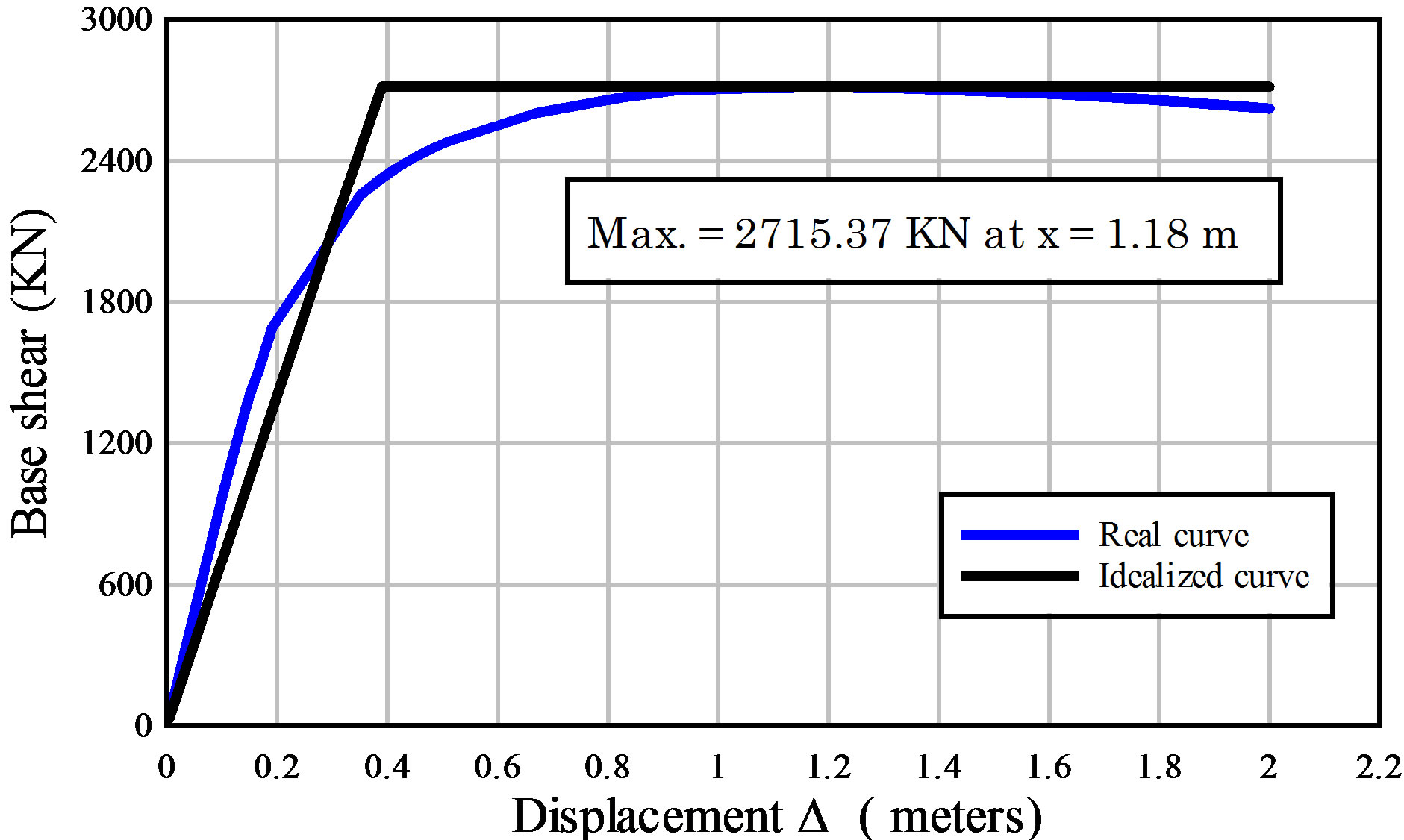
Figure 3. Idealized and real capacity curves. Frames A = D. 14 story model.
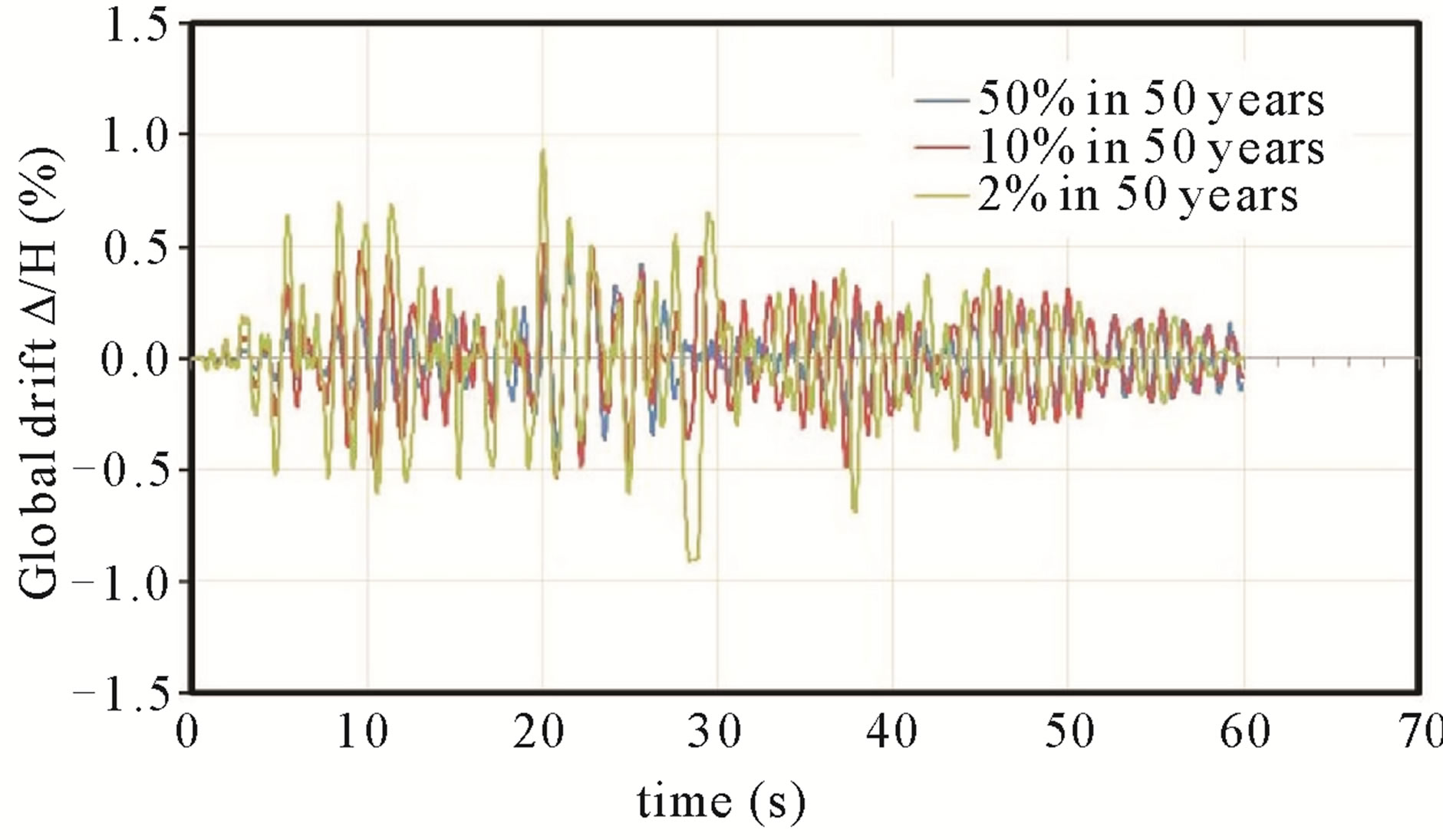
Figure 4. 14 stories building. Frames A = D. 60 seconds earthquake.
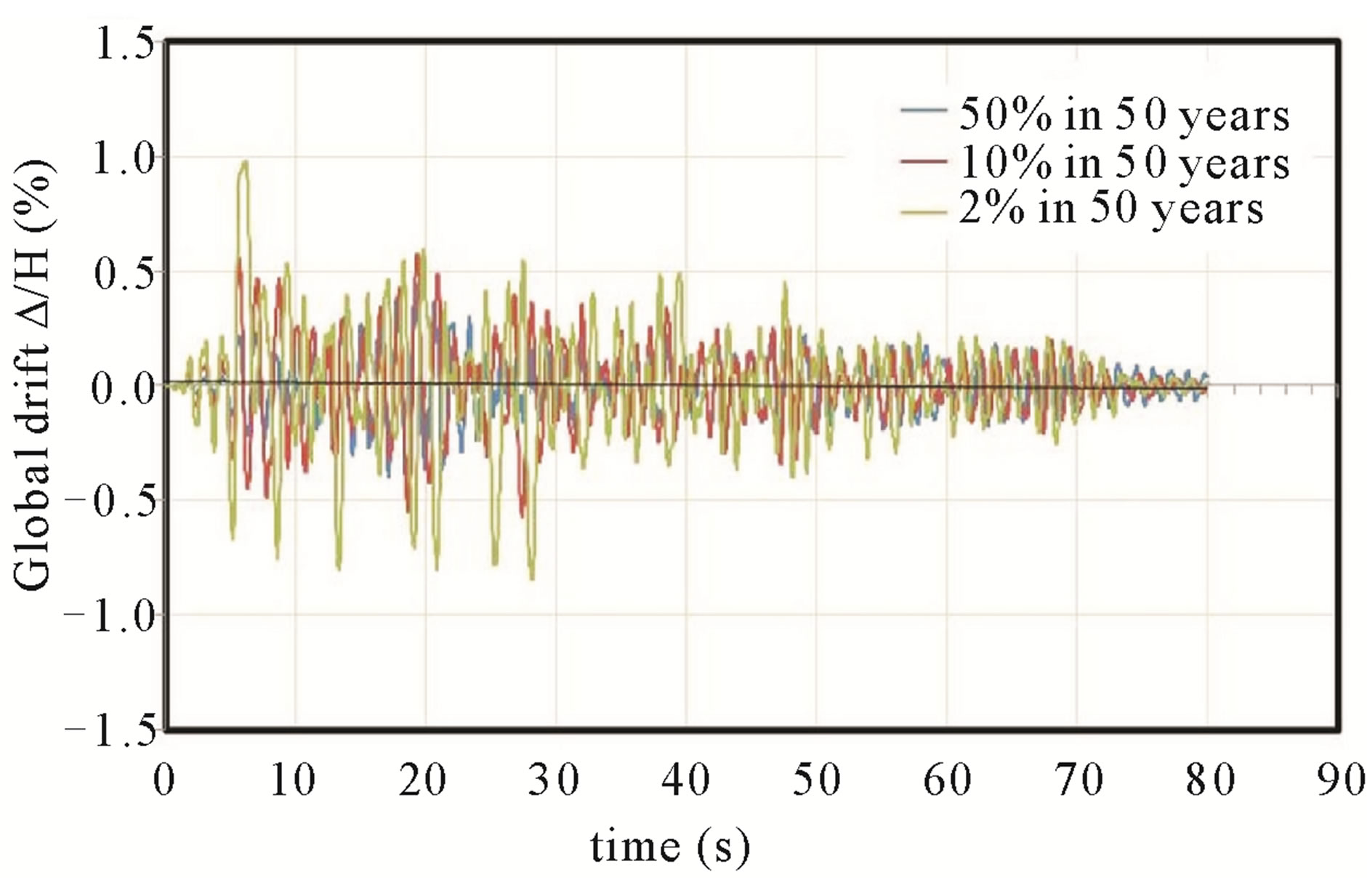
Figure 5. 14 stories building. Frames A = D. 80 seconds earthquake.
the 2 = 3 non V-braced frames presented higher values than 1.5% for the rare earthquake and 3% for the very rare earthquake, indicating a possible collapse in the structure. This implied a redesign of those frames, gradually increasing all columns, until obtained drifts lower than maximum allowed. Graphics for inter story drifts for the frames of the 14-story building, acting the earthquake of 60 seconds are presented in Figures 7-9.
4. CONCLUSIONS
From the capacity curves it can be concluded that Vbraced spans in the outer frames allows to increase the capacity of the structure to withstand lateral loads before the collapse. By finding a response reduction factor (R)
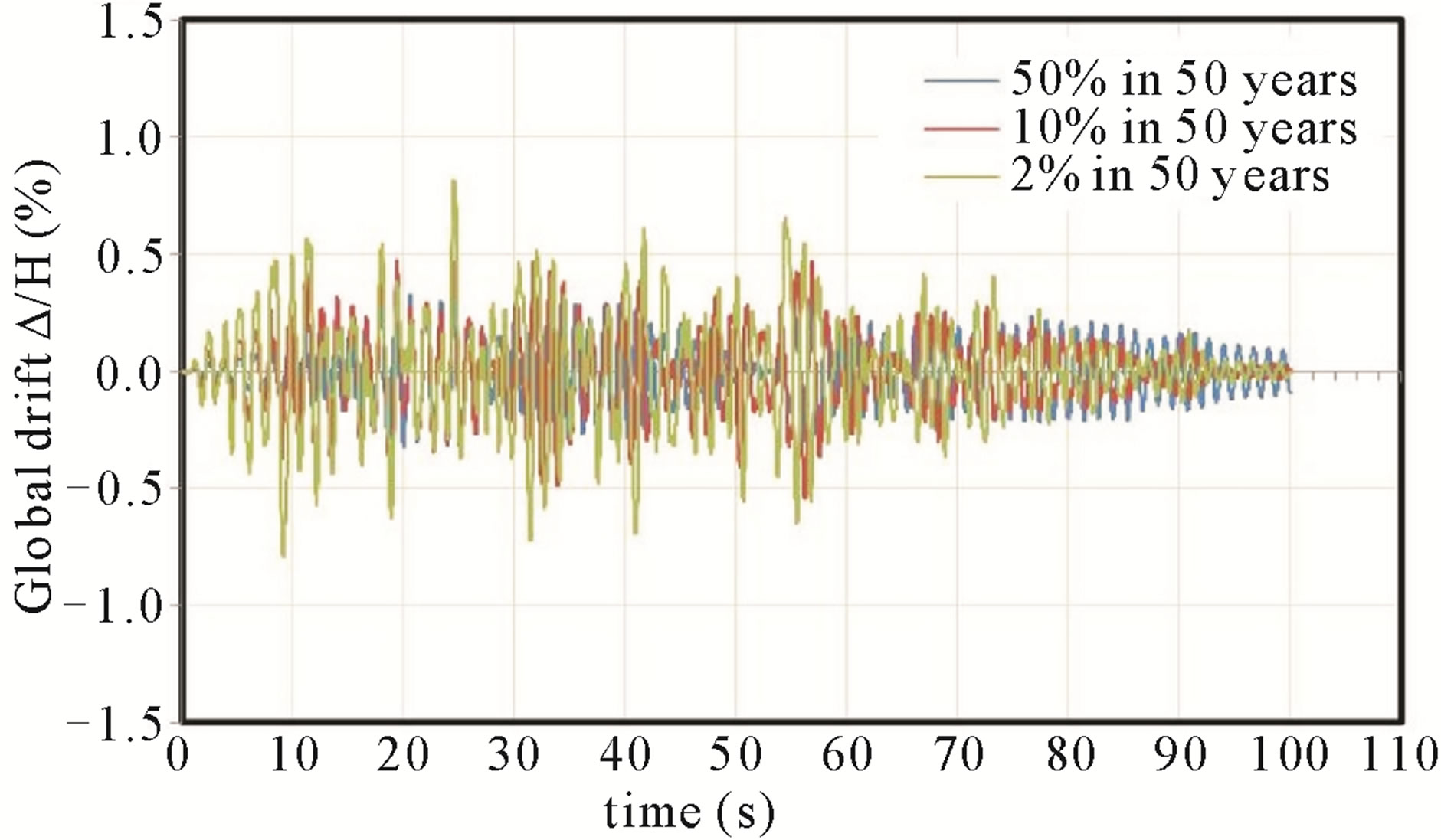
Figure 6. 14 stories building. Frames A = D. 100 seconds earthquake.
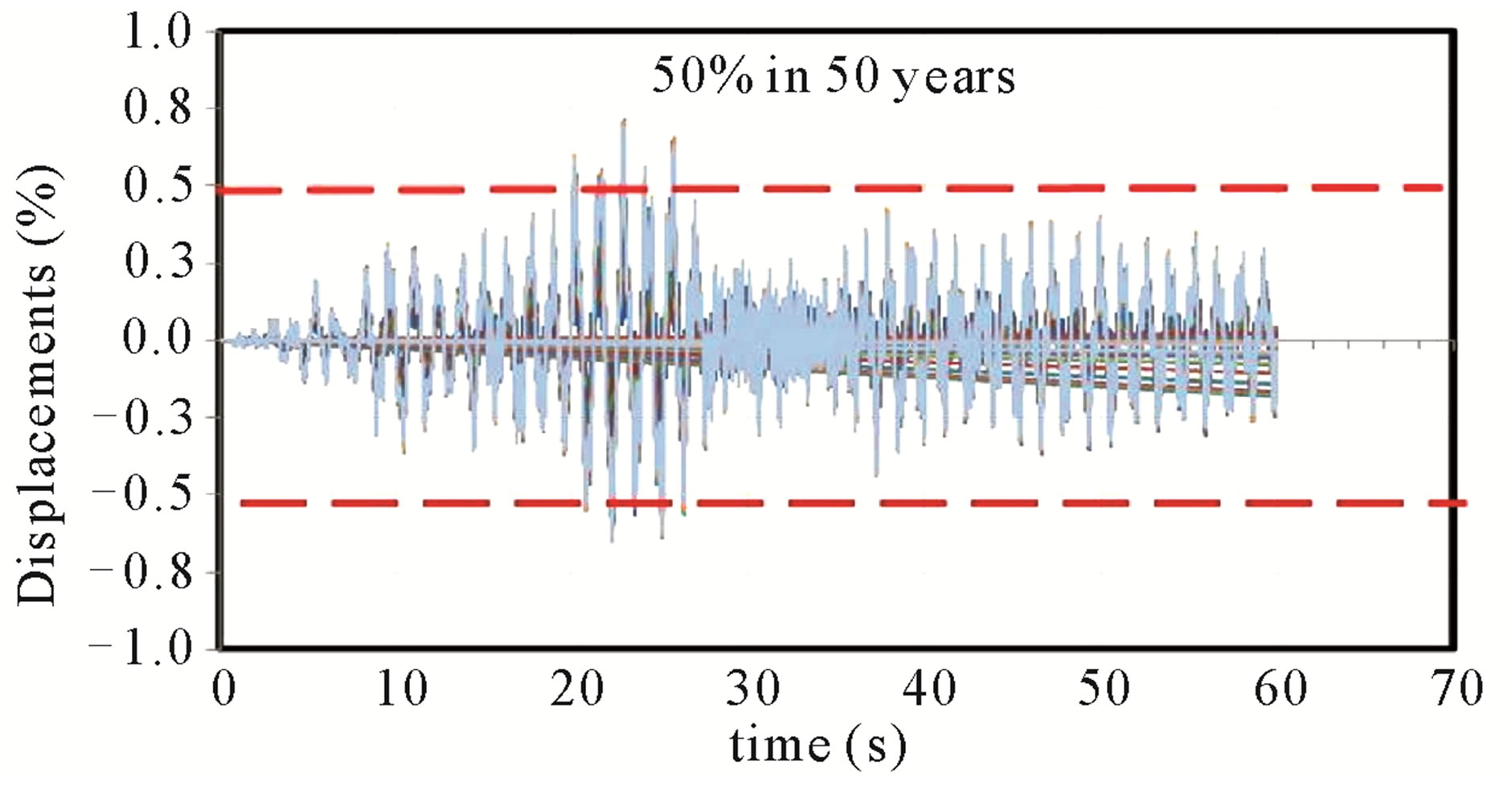
Figure 7. 14 stories building. Frames A = D. Frequent earthquake. Duration: 60 seconds.
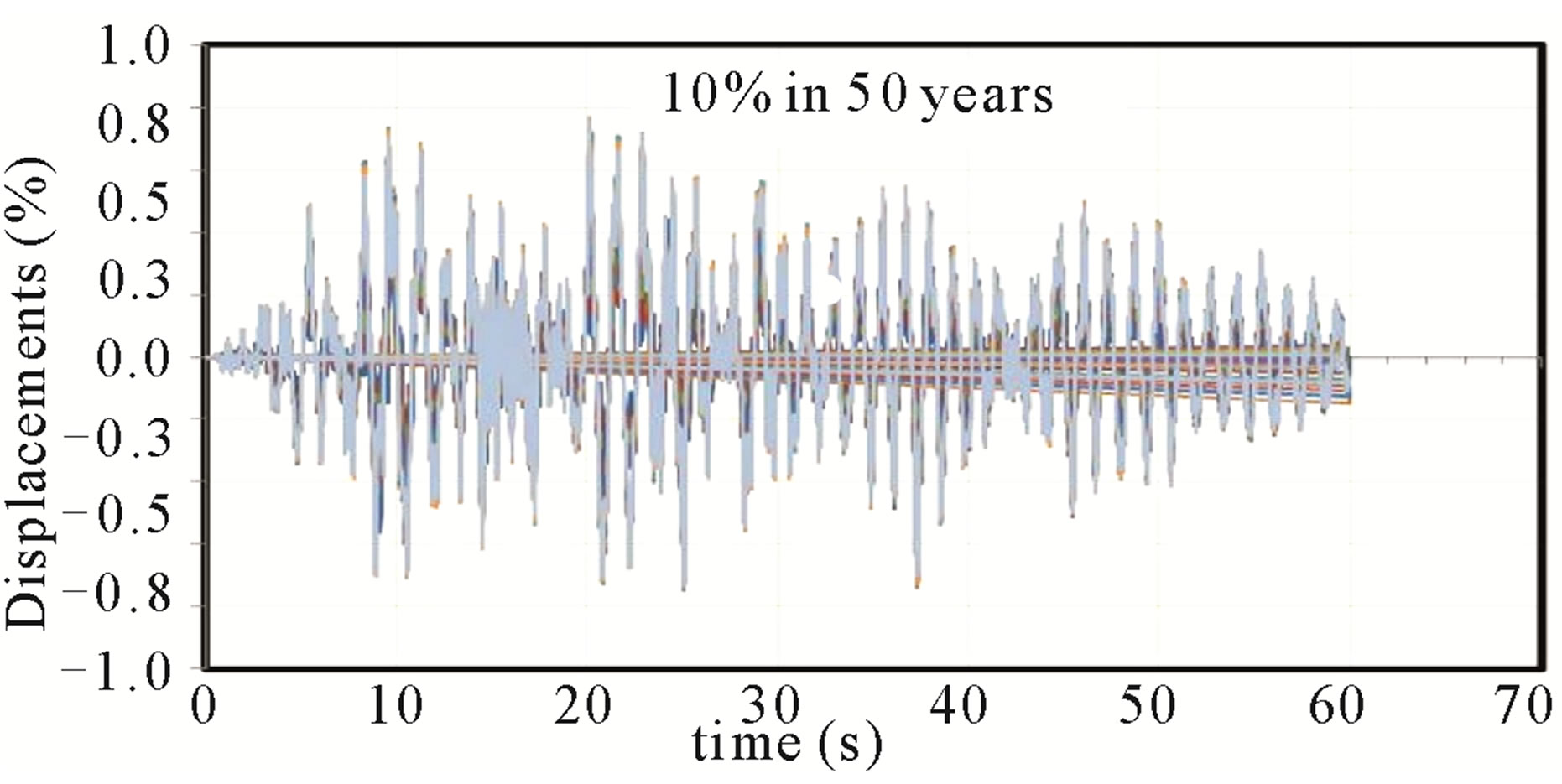
Figure 8. 14 stories building. Frames A = D. Rare earthquake. Duration: 60 seconds.
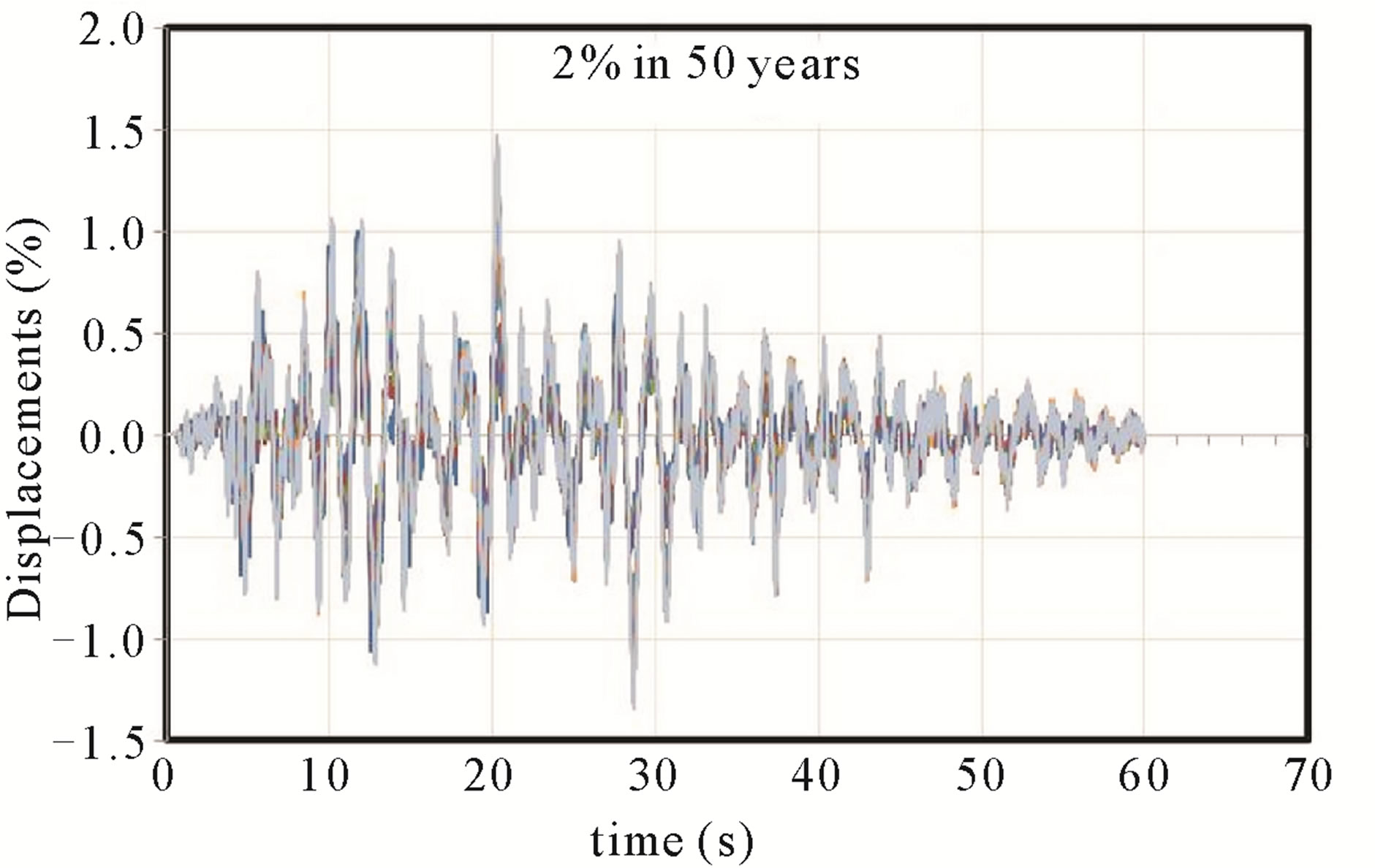
Figure 9. 14 stories building. Frames A = D. Very rare earthquake. Duration: 60 seconds.
exceeding the factor considered in the design, is concluded that these structures are reliable in their seismic performance. It was noted that response reduction factors are large while decreases the height of the building. It was determined that as the height increases, the over decreases, indicating that low-rise structures have greater capacity for lateral resistance after reaching the yielding point.
The values of global drifts showed that structures may have damage in the non-structural elements under frequent or rare earthquake and can show repairable damage in some structural elements under a very rare earthquake without reaching the collapse of the structure. However, to compare these global drifts with the values of inter story drifts, some frames were detected with differences with this trend; by that, damage could be present in certain structural elements until collapse of the structure if not redesigning these frames. It’s concluded that it is not enough to verify the value of the global drifts since small displacements on certain floors could compensate for excessive displacements in others, getting global values below the maximum limit, but still reaching the collapse of the structure. Drifts in the Vbraced frames were lower than in non V-braced frames, concluding that the performance of the structure is improved when using diagonals concentric type inverted V bracing. In addition, in the case of V-braced frames, the largest drifts occurs at upper stories while in not Vbraced frames, drifts were higher in the lower levels. It’s possible to conclude that V-braced frames in high-rise buildings improves the resistant capacity of the structure for gravity and lateral loads, finding still better behavior in low-rise buildings, which agrees with Bermúdez [13].
Although the earthquake resistant buildings design prescribed by Venezuelan code takes into account the plastic range of the loads through the reduction R factor, also allows the elastic analysis; on the other hand, steel structures design code defines elastic-plastic Limits States for structural members considering the plasticity of materials. These possible incompatibilities between elastic and plastic behavior in the same design considerations can mean that obtained results in the elements are not reliable enough. The LRFD method aims to obtain an adequate structural behavior for every member of a structure, but this means that variables associated with the structural system as a whole are not considered. Thus, the code assumes that a structure will be effective as long as all members are appropriate, but are not considered factors as ductility, structural redundancy and configuration correlation among loads and combined structural resistance, Li and Li [14]. All this can result in a not realistic enough structural design with less accurate values of behavior expected by the designer and the earthquake resistant design code.
Findings of this study are applicable to a specific type of building, so the study of other configurations is important to calibrate the results with the buildings studied here. It is advisable the study of mechanical models that could cover other combinations of types, numbers of stories spans lengths, height of columns and seismic hazard levels. Results show that seismic loads are supported largely by the lateral bracing, so it can be very appropriate to investigate the mechanism and extent of load transfers to other structural elements under an event that could cause lateral bracing collapses. Overall, these findings improve the knowledge about seismic and structural behavior of this type of structural typology, therefore validating non linear dynamic analysis as a very powerful tool to seismic-resistance design and the use of Chevron-braced frames as a very useful choice in improving the response of tall steel structures, considering that this type of lateral bracing is currently absent from the Venezuelan seismic codes.
REFERENCES
- Longo, A., Montuori, R. and Piluso, V. (2009). Seismic reliability of V-braced frames: Influence of design methodologies. Journal of Earthquake Engineering, 12, 1246- 1266. doi:10.1080/13632460802211867
- Alonso, J. (2007). Seismic vulnerability of buildings. Fondo Editorial Sidetur, Caracas.
- COVENIN (2001) Earthquake resistant design code 1756:01. Ministerio de Fomento, Caracas.
- COVENIN (1988) Minimum actions and criteria for buildings projects code 2002:88. Ministerio de Fomento, Caracas.
- COVENIN (1998) Steel structures for buildings. Limit States method 1618:98. Ministerio de Fomento, Caracas.
- Song, J. and Ellingswood, B.R. (2009) Seismic reliability of special moment steel frames with welded connections: I. Journal of Structural Engineering, 125, 18266.
- Vielma, J.C., Barbat, A.H. and Oller, S. (2009). Nonlinear structural analysis. Application to evaluating the seismic safety. Nova Science Publishers. New York.
- Dolsek, M. (2008) Incremental dynamic analysis with consideration of modeling uncertainties. Earthquake Engineering & Structural Dynamics, 38, 805-825. doi:10.1002/eqe.869
- Vielma, J.C., Barbat, A.H. and Oller, S. (2001) Framed structures earthquake resistant project. International Center for Numerical Methods in Engineering Monograph, Earthquake Engineering Mongraphs, Barcelona.
- Elnashai, A., Papanicolau, V. and Lee, DH. (2011). Zeus NL—A system for inelastic analysis of structures: User manual. Mid-America Earthquake Center (MAE), Urbana.
- UCLA-CIMNE (2009) Compatible accelerograms with elastic design spectrums generation programm (PACED). International Center for Numerical Methods in Engineering, Venezuela.
- Elnashai, A. and Di Sarno, L. (2008). Fundamentals of earthquake engineering. John Wiley and Sons, Chichester. doi:10.1002/9780470024867
- Bermúdez, C.A. (2010). Seismic vulnerability of steel buildings. Ph.D. Thesis, Universidad Politécnica de Catalunya, Barcelona.
- Li, G.-G. and Li, J.-J. (2007). Advanced analysis and design of steel frames: First review. John Wiley & Sons Ltd, London.

