ABSTRACT

Monte Carlo simulation of two dimensional 4 state Potts model has been carried out in microcanonical ensemble. The simulations were done on a 30 × 30 system with periodic boundary conditions. The temperature dependence of energy and order parameter has been calculated. The transition in 4-state Potts model is concluded to be first-order in nature. The transition temperature and latent heat of the first-order transition have been found to be 0.92 and 0.18, respectively.

Keywords:

Microcanonical Monte Carlo, Potts Model, First-Order Transition

1. Introduction

The two dimensional (2D) q-state Potts model undergoes a well studied transition (first-order or higher-order) and provides a system of increasing complexity as q increases [1] [2] . The Potts model has been used to gain an understanding of the phase transition in the presence of kink defects. It is also interesting in the context of lack-of-ergodicity and deviation from the usual exponential probability [3] . The Potts model has been studied theoretically and expression for the transition temperature (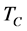), latent heat and discontinuity of the order parameter (magnetization) have been given in the literature [4] - [7] . There has been a lower limit of 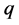in Potts model below which the transition ceases to be first-order. The limit has been given in the literature to be. Since the theoretical results are based on certain assumption, there has been a need to supplement it with Monte Carlo simulations [8] - [14] . In an experimental study of first-order transition energy is added to (removed from) the system and the resulting physical quantities are measured. The microcanonical Monte Carlo simulation closely represents this situation and therefore it is expected to give reliable results for the transition [11] [12] [15] [16] [17] . The rationale for the present work had been to compare theoretical and Monte Carlo simulations results to better accuracy. Here we present microcanonical Monte Carlo simulations for 4-state Potts model and conclude that the transition is first-order in nature.

2. Hamiltonian for Potts Model

In the Potts model the spin at the ith site 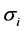can take any one of the 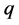different or distinct values and therefore called q-state. If the spin states are equal between any two neighbors then the energy due to interaction is J otherwise it is zero. It is stated mathematically as. For the system shows possibility for statistical variation and hence thermodynamic-like quantities can be obtained from Monte Carlo simulation. The spins are assumed to interact with their 4 neighbors in a square lattice (2D). The Hamiltonian of the q-state Potts model is given by

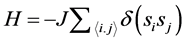(1)

where J is the interaction strength (>0 for the ferromagnetic case) and the sum is over all the nearest neighbors on a square lattice. It has been suggested that the Potts model has a first-order transition for 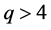and for 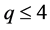there is higher order transition [2] .

We consider a 2D square lattice having 900 spins with periodic boundary conditions and simulated the system for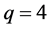. Initially all the spins are aligned in one sate (i.e., state 1) which corresponds to the lowest energy of the system. An extra degree of freedom called the “demon” is allowed to move from one spin site to another sequentially on the lattice as it exchanges energy with spins changing the microstate. The simulation starts with the demon having a fixed amount of energy (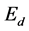). This demon energy when added to the system energy (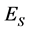) corresponds to the total energy of the system at the lowest desired temperature. A random number in the interval 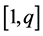is generated which corresponds to a possible new state of the spin. The change in energy is calculated corresponding to this change in spin state. A positive change in energy is allowed if the demon has sufficient energy. Otherwise the old spin state is retained. A negative or zero change in energy is always accepted and the demon receives that amount of energy from the spin system. The criterion of choosing the random number and accepting the change of configuration as described above satisfies a restricted form of detailed balance. The demon here takes energy values that are integral multiples of J. After the system attains equilibrium the distribution of 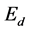corresponds to the well known exponential that is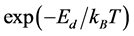. Since the system energy is discrete we find the following equation valid for Potts model to determine the system temperature from the average demon energy [11] .

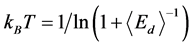(2)

where 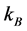is the Boltzmann constant. Hereafter we replace by and by for simplicity. The order parameter m is defined as follows:

(3)

where is the number of spins in state 1, is the number in state 2 etc.; is the maximum of; and is the total number of spins.

The equilibration and the nature of the fluctuation of the order parameter with this algorithm has been studied before and has been found that 1 × 10⁵ Monte Carlo step per spin (MCSS) are sufficient for equilibration and averaging of the physical quantities.

3. Monte Carlo Simulation Result

The expression for the exact value of the transition temperature () in the Potts model is given as follows:

(4)

For we obtain the exact value of from Equation (4) which is nearly 0.91. Simulations were done with 4 × 10⁵ MCSS for equilibration and 4 × 10⁵ MCSS for averaging. The simulation constituted of a cooling run followed by a heating run. The physical quantities computed are averages of the heating and cooling runs. Figure 1 shows the system energy per spin as a function of temperature which shows a discontinuity at T = 0.92. For a first-order transition a discontinuity arises in T vs. E due to latent heat. A 1^st order transition is characterized by three regions in T vs. E which are high and low temperature regions and the latent heat region with constant temperature. Monte Carlo simulation in microcanonical ensemble, a 1^st order transition appears as S'-bend. The 1^st order transition is characterized by negative specific heat which is the equilibrium response of a finite isolated system [15] . The width of the transition reduces as lattice size is increased [16] . Although situations are known where negative specific heat changes to positive value as the system size is increased [17] here the latent heat region did not reduce as the system size is increased to 60 × 60. We also observed negative specific heat when the MCSS is increased to 1 × 10⁷ in the 30 × 30 spin system. Therefore, we conclude that 4-state Potts model has 1^st order transition. The latent heat involved in this transition is about 0.18 and T_C agrees with the exact value. Figure 2 shows the temperature dependence of the average order parameter. It is seen that shows a discontinuity at T = 0.92 as expected for a first-order transition.

4. Conclusion

In conclusion we have studied the 2D Potts model for using microcanonical Monte Carlo simulation. It has been concluded that it shows a first-or- der transition unlike that previously reported in the literature (as higher order).

The transition temperature has been found to be 0.92 and the latent heat involved in the transition is about 0.18.

Cite this paper

Ota, S.B., Ota, S. and Ota, A. (2017) Microcanonical Monte Carlo Simulation of 2D 4-State Potts Model. Journal of Modern Physics, 8, 602-606. https://doi.org/10.4236/jmp.2017.84040

References