Journal of Modern Physics
Vol.07 No.01(2016), Article ID:62955,5 pages
10.4236/jmp.2016.71013
Confining Potential and Mass of Elementary Particles
Lev I. Buravov
Institute of Problems of Chemical Physics RAS, Chernogolovka, Russia

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 July 2015; accepted 18 January 2016; published 22 January 2016
ABSTRACT
In this paper we consider a model in which the masses of elementary particles are formed and stabilized thanks to confining potential, which is caused by recoil momentum at emission of specific virtual bosons by particle itself. The calculation of this confining potential Ф(R) is carried out. It is shown that Ф(R) may be in the form const ּR3 or const ּR2 depending on continuous or discrete nature of the spectrum of emitted bosons.
Keywords:
Confining Potential, Origin of Mass of Particle, Stabilizing of Particle Mass, Virtual Bosons, Spherical Bosonic Wave, Origin of Neutrino Masses, Neutrino Mass Formula, Calculation of Neutrino Masses

1. Introduction
In the article the model of formation of mass of elementary particles is offered as a result of emitting of the special virtual bosons as spherical waves (conditionally we will name them as the bosons of Higgs). It is supposed here that confining potential which is necessary for stabilizing of particle mass appears because of effect of impulse recoil, especially for electron, muon, pion, kaon and neutrino.
In due time Poincare, proceeding from common sense, entered supposition about a presence in the structure of electron of some elastic elements due to which the charge of electron holds out in a small volume. This model was later used by many authors. We will consider it more detailed, following [1] [2] .
In accordance with [1] [2] virtual rest energy of electron Е consists of two parts: surface energy of elastic shell 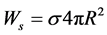 and electrostatic energy of the charged surface
and electrostatic energy of the charged surface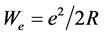 , where σ is the coefficient of surface tension of the shell,
, where σ is the coefficient of surface tension of the shell, 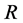 is its radius,
is its radius, 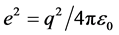 ,
, 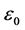 is dielectric constant of vacuum, q is an electron charge (in units of SI). Virtual rest energy of such system is equal to:
is dielectric constant of vacuum, q is an electron charge (in units of SI). Virtual rest energy of such system is equal to:
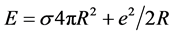 (1)
(1)
The radius of electron, corresponding to a minimum of energy (1) of the system, is determined from equation 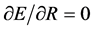 and is equal to:
and is equal to:
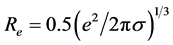 (2)
(2)
From Equations (1) and (2) the mass of electron is

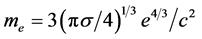 (3)
(3)
It is possible also to write down that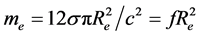 , where a σ value was determined in [3] with using the value of neutral pion mass
, where a σ value was determined in [3] with using the value of neutral pion mass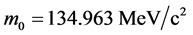 :
:
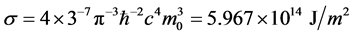 (4)
(4)
and coefficient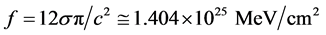 .
.
In Equation (1) the value  obviously fulfills the role of confining potential due to which the mass of electron is stabilized.
obviously fulfills the role of confining potential due to which the mass of electron is stabilized.
Preliminary we will represent information about the calculation of the masses for several elementary particles and then pass to more detailed consideration of confining potential.
In [3] the calculation of the ratio for the masses of the particles e, 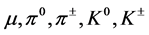
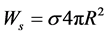
radius of elastic shell, σ is the coefficient of surface tension, the same that is in Equations (1)-(4). In [3] it was shown that virtual rest energy of these particles can be written down in general case in some more complex forms, than those for an electron:
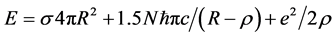
where ρ is a radius of the compressed electric cloud, and N is the number of neutrino quanta that is determined from the decay scheme: N = 2 for muon, 3―for pion, and 21―for kaon. The masses of particles and characteristic sizes 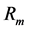
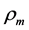
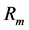
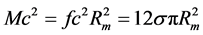
It is assumed in the Standard Model that the masses of row of elementary particles can be represented in the form:
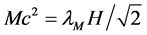
where H = 246 GeV is the characteristic energy in the model of Higgs [4] [5] , 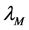
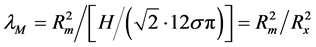
where unknown size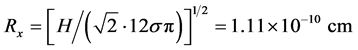
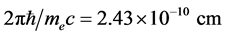
The result of the Formula (6) was used in [6] for the calculation of neutrino masses 
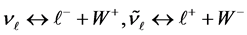
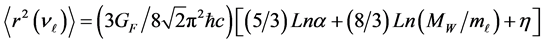
where 


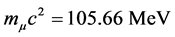

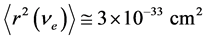
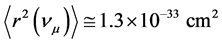
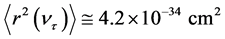
To define the masses of neutrino in [6] simple suppositions are made:
1. Although neutrinos do not have an electric charge, they seems to have small electrostatic energy due to that spacial distributions of diverse charges produced by virtual pairs 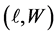

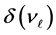
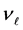
2. Virtual rest-energy of neutrino consists of the confining potential 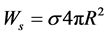
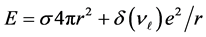
3. The value of s is identical for all neutrinos.
Similarly, as for an electron, mass of neutrino would be found at being of a minimum of virtual energy (11):

but as a value 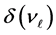
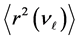
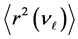
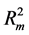
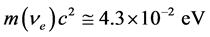
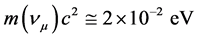
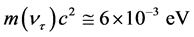
Similar values for three neutrino mass eigenstates (ν1, ν2, ν3) were received in [11] on the basis of Super-Ka- miokande experimental results [12] , inventively solving system of two equations with 3 unknown quantities, if supposing the case of inverted mass spectrum.
Values 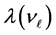

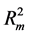
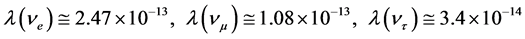
We will notice that as 
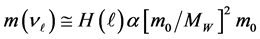
where a dimensionless factor 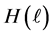
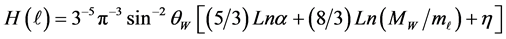
θw―is the angle of Weinberg, 
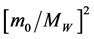
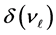
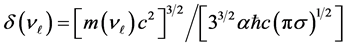
and are equal to:
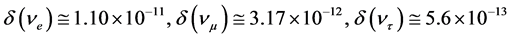
In Equation (5), also as in (1), the value 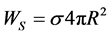
So then for the ground of this model we will enter next suppositions:
1. By analogy with the model of Poincare we will suppose that every elementary particle has confining potential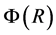
2. Every elementary particle radiates the special virtual bosons as spherical waves

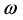
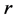
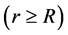
3. We will suppose that mass of such bosons 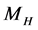
tence of such virtual bosons τ is much smaller than 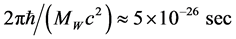
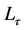
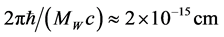
4. Every elementary particle is the inexhaustible source of such virtual spherical waves, but the mass of the particle-source does not decrease, because virtual bosons through an instant τ return back into a source, due to interacting with the fields of vacuum.
5. We suppose that complete amount of the bosons emitted by a particle in a unit of time NH is proportional to area of particle surface with a coefficient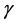
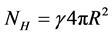
As every moving wave carries an impulse, it ensues from these suppositions, that on the surface of elementary particle because of the effect of impulse recoil, spherical waves are creating holding force of pressure F(R) and confining potential
We will consider 2 cases for forms of boson spectrum:
a) the emitted bosons have a continuous spectrum of radiation in the interval of 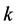
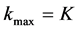
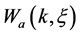
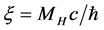
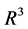
b) the emitted bosons have a discrete spectrum of radiation : 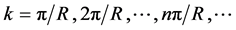
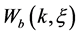
Let’s consider the case of a). We will enter the condition of normalizing for 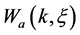
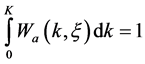
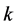
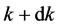

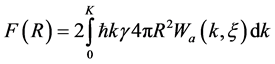
Consequently confining potential for the case of a) is:
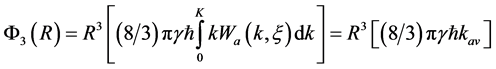
where 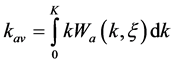
For the case of b) we will enter the condition of normalizing for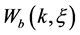
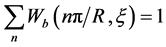
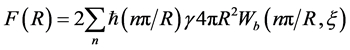
The sum 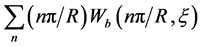
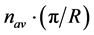
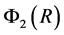
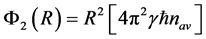
Thus, in the article it’s assumed that every elementary particle produces the special bosonic field that is present only in a thin layer at the surface of a particle. It is shown that this field can create the confining potential, stabilizing the mass of particle during the time of its life.
Cite this paper
Lev I.Buravov, (2016) Confining Potential and Mass of Elementary Particles. Journal of Modern Physics,07,129-133. doi: 10.4236/jmp.2016.71013
References
- 1. Dirac, P.A.M. (1962) Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences, 268, 57-67.
http://dx.doi.org/10.1098/rspa.1962.0124 - 2. Feynman, R., Leighton, R. and Sands, M. (1964) The Feynman Lectures on Physics, Vol. 2. Addison Wesley Pub. Com., Massachusetts, Palo Alto and London.
- 3. Buravov, L.I. (2009) Russian Physics Journal, 52, 25-32.
http://dx.doi.org/10.1007/s11182-009-9196-5 - 4. Quigg, C. (2007)
http://arxiv.org/pdf/0704.2232.pdf - 5. Vysotsky, M.I. (2011) Physics of Particles and Nuclei Letters, 8, 617-650.
http://dx.doi.org/10.1134/S1547477111070181 - 6. Buravov, L.I. (2013) Russian Physics Journal, 55, 1368-1369.
http://dx.doi.org/10.1007/s11182-013-9968-9 - 7. Bernstein, J. and Lee, T.D. (1963) Physical Review Letters, 11, 512-516.
http://dx.doi.org/10.1103/PhysRevLett.11.512 - 8. Lee, T.D. and Sirlin, A. (1964) Reviews of Modern Physics, 36, 666-669.
http://dx.doi.org/10.1103/RevModPhys.36.666 - 9. Cheng, W.K. and Bludman, S.A. (1964) Physical Review, 136B, 1787-1790.
http://dx.doi.org/10.1103/PhysRev.136.B1787 - 10. Particle Data Group (2012) Reviews, Tables, Plots.
- 11. Hajdukovic, D.S. (2011)
http://arxiv.org/abs/1106.5810 - 12. Nakamura, K. and Petcov, S.T. (2010) Journal of Physics G, 37, 164-183.
- 13. Prokhorov, A.M., Ed. (1992) Physics Encyclopedia, Vol. 5. Sovetskaya Entsiklopedia, Moscow. (In Russian)