Journal of Modern Physics
Vol.06 No.08(2015), Article ID:58288,6 pages
10.4236/jmp.2015.68118
Temperature and Concentration under Boundedness
Maria K. Koleva
Institute of Catalysis, Bulgarian Academy of Sciences, Sofia, Bulgaria
Email: mkoleva@bas.bg
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 June 2015; accepted 21 July 2015; published 24 July 2015
ABSTRACT
In the present paper I have proved that in the setting of recently introduced concept of boundedness the intensive macroscopic variables such as temperature and concentration are well-defined even for structured objects and nano-objects. I have proved that the Poisson distribution is generic distribution for all fluctuations. An indispensable part of the proof is the existence of a general dynamical mechanism which provides damping out of the arbitrary accumulation of matter/ energy in every given location and in every moment.
Keywords:
Fluctuations, Poisson Distribution, Boundedness

1. Introduction
Thermodynamics and statistical physics are one of the most powerful tools of modern interdisciplinary science. Their supremacy is grounded on the fact that these approaches are equally available for the widest scope of systems ranging from nano-systems to living organisms to cosmic objects. On the other hand, their power is built on the postulate that the macroscopic variables are divided into two sub-classes: intensive and extensive variables so that the intensive ones do not depend on the shape and size of a system while the extensive ones exhibit linear dependence on the size of a system. The most important intensive variables are temperature and concentration. The temperature is defined as a measure for the average velocity of the species while concentration is defined as the average number of species at a given physically infinitesimal volume.
Although this postulate works remarkably well, it still suffers severe flaws when considering nano-objects or structured objects such as living organisms. In the first case the considerable growth of the fluctuation size compared to the mean value gives rise to the question whether it is ever possible to define the notion of intensive variable. Indeed, according to the statistical mechanics, the weight of fluctuations increases as 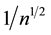 on decreasing the size of a system n. This problem acquires an immense importance in view of the demand for further downsizing of nano-objects.
on decreasing the size of a system n. This problem acquires an immense importance in view of the demand for further downsizing of nano-objects.
The second flaw concerns structured objects such as living organisms where complicated bio-chemical reactions proceed permanently. It is well known [1] that because every reaction, along with the corresponding diffusion, defines specific size in the system, it should be expected that the web of bio-chemical reactions would prevent living organisms from steady functioning. Moreover, since the presence of specific sizes in a system yields violation of the Poisson distribution [1] , it is to be expected an uncontrolled growth of fluctuations of all sizes and shapes.
These flaws outline the important role which fluctuations play in defining the macroscopic variables. The problem is particularly important for the basic macroscopic variables such as temperature and concentration since the lack of damping mechanism for fluctuations renders impossible assigning of probability distribution to the fluctuations. This happens because the lack of damping renders the average velocity and the average number of species in any point to depend on the number of species involved in their determination. This, however, contradicts the basic assumption of probability theory that neither distribution depends on the number of species involved [2] .
The successful overcoming of the above flaws constitutes the major goal of the present paper. Yet, the way to its resolution faces the following dilemma: is it ever possible to resolve the above paradoxes in the setting of the traditional statistical mechanics or one should adopt a novel paradigm for this purpose. A lot of papers are written in favor of the first alternative. The major approaches are: the one called dissipative structures developed by Prigogine and co-workers [1] ; the second major approach has been introduced by [3] where it is considered that the species movement is random but happens with bounded velocity. The accent of the enormous amount of papers is put on the memory effects produced by the boundedness of the velocity.
However, I have proved [4] that the boundedness of the velocities alone yields an unexpected amplification of the fluctuations which makes the above approach inappropriate. For this purpose I have redeveloped the idea of boundedness so that it acquires dynamical origin whose major property is that it provides automatic control over fluctuation growth. The major advantage of that mechanism is that its operational protocol is available for the widest scope of systems: ranging from the nano-objects to the living organisms to the cosmic objects.
Another advantage of the concept of boundedness introduced by me is that it provides that weight of fluctuations always inversely proportional to the size of the system. In section 2 I will prove that this condition is necessary and sufficient one for providing the availability of the Poisson distribution for the fluctuations at each and every system.
In Section 3, I will demonstrate the operational protocol which provides the dynamical control over the fluctuations grow. Yet, it should be stressed that it acquires novel meaning: it is measure for the average relative velocity among species.
In the next section I will make a brief introduction to the concept of boundedness which I put forward recently [5] and whose systematic development can be found in my recently published book [6] . A particular stress is put on the highly non-trivial interplay among all components of that concept. This is made because some of these components are present in other popular concepts of interdisciplinary science but the effect of their presence is very different compared to the concept of boundedness where their synergy gives rise to unexpected consequences.
2. Concept of Boundedness in a Nutshell
The concept of boundedness has been introduced [5] [6] for explanation of the ubiquitous coexistence of specific and universal properties of complex systems. It grounding assumptions concern the major protocol of the response of complex systems. The most amazing property of the ubiquitous coexistence of universal and specific properties is that it is shared by both intelligent and non-intelligent complex systems. That is why I have introduced several grounding assumptions about the response of all complex systems along with additional assumptions how further the response of the sub-class of intelligent complex systems is organized. Since the subjects of consideration of the present paper are temperature and concentration, I will present only the grounding assumptions for the response of the widest class of complex systems which comprises both the non-intelligent and intelligent ones.
The concept of boundedness consists of mild assumption that the rate and the amplitude of matter/energy/ information that a system exchanges with its ever-changing environment are permanently bounded and stay within specific margins. The response itself can “adapt” locally its specific rule so that to fit within the above margins. Another assumption which I will discuss in details in Section 3 is that the relative velocities must also be kept bounded.
The comparison with two other theories of the complex systems which comprise certain aspects of the concept of boundedness but not all of them highlights better the highly non-trivial interplay among all components of the concept of boundedness.
Let me start the comparison with the theory of deterministic chaos. It is a theory where a given non-linear mapping, defined in a bounded domain of admissible values, produces a stochastic sequence as a solution at certain values of the control parameters [7] . For the sake of clarity let me present this property on the example of logistic mapping:
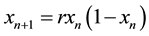 (1)
(1)
where 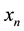 is the population of a given species set at constant environment defined through the control parameter r. Obviously the population is defined only in the range
is the population of a given species set at constant environment defined through the control parameter r. Obviously the population is defined only in the range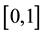 . Then, on reaching a value greater than 1, the value of
. Then, on reaching a value greater than 1, the value of 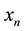 “jumps” to the difference between that value and 1 and the process starts again. Further, for the values of r about 4, the solution turns stochastic.
“jumps” to the difference between that value and 1 and the process starts again. Further, for the values of r about 4, the solution turns stochastic.
Thus, it becomes apparent how and to what extend the boundedness enters the basic assumptions of the deterministic chaos. That is: first the deterministic chaos involves boundedness of the amplitudes through restraining the set of admissible values to a bounded region. Second it involves the idea of non-homogeneity since the rule “adapts” its form depending on whether the current value of 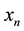 is within the domain of admissible values or it exceeds it. To remind, on exceeding the thresholds, the rule is given by a “jump” to the beginning of the range. Thus, we have two basic assumptions of the theory of boundedness in hand and one basic assumption of the concept of boundedness missing: The missing assumption is boundedness of the rates. Next I will consider how critical the absence of that assumption is for the deterministic chaos.
is within the domain of admissible values or it exceeds it. To remind, on exceeding the thresholds, the rule is given by a “jump” to the beginning of the range. Thus, we have two basic assumptions of the theory of boundedness in hand and one basic assumption of the concept of boundedness missing: The missing assumption is boundedness of the rates. Next I will consider how critical the absence of that assumption is for the deterministic chaos.
Indeed, it is well-established fact that the power spectrum of the chaotic solutions is white noise not 1/f noise which is typical for complex systems. White noise implies lack of correlations among members of the corresponding power spectrum. This result is to be excepted because the “jumps” from the one end of the domain of admissible values to the other eliminate the correlations among successive steps created by the successive application of the specific rule that defines any given mapping. What does the boundedness of the rates change in this frame so that to expect 1/f shape of the power spectrum? It is that the boundedness of the rates “keeps” the distance between successive steps within a given margins. In result, distant steps turn correlated. It should be stressed on the fact that these correlations are not a result of specific physical process but they are purely of mathematical origin.
The second very popular theory of complex systems, the so called Self-Organized Criticality (SOC), has been introduced by Bak et al. [8] where “self-organized” means that starting from any initial condition, the system tends to move toward a critical state and stay there, without external control. This supposition is held by means of keeping the rates of development of avalanches bounded which turns into sliding when the thresholds are exceeded. This theory successfully explains the 1/f shape of the power spectrum but it fails to explain the coexistence of specific and universal properties of any system. Another serious flaw is that it is not able to quantify any relation system-response. This implies that even tiny perturbation can trigger a large avalanche. At the same time at a next run, the same perturbation can trigger an avalanche of completely different size. This flaw is result of the lack of boundedness over the amplitude of growing the avalanches.
The highly non-trivial interplay between all aspects of the concept of boundedness renders its exclusive property to be the existence of presentation basis (which is power spectrum) where the response decomposes additively into two parts: a specific discrete pattern, called homeostasis, and a continuous noise component whose shape is universal. The homeostatic pattern is robust to environmental changes. Since the shape of the noise component is also robust to the environmental changes, the separation of the homeostatic pattern happens with constant accuracy.
In turn this constitutes the fundamental difference between the concept of boundedness and the above theories. Indeed, while both the deterministic chaos and SOC implies total unpredictability of the future behavior of a system, the above central result implies that the future behavior of every complex system is predictable up to predictability of its homeostasis.
3. Poisson Distribution under Boundedness
The Poisson distribution is one of the most popular statistical distributions because its interpretation has widest scope of availability. Indeed, it is supposed that the Poisson distribution gives the probability for occurring of an event among other uncorrelated events. Thus, it is widely used for defining the notion of concentration since it is supposed that the current positions of different species are uncorrelated in view of the random motion and number of binary collisions they exerted.
However, this setting suffers the following fundamental flaw: The supposition about lack of correlations among different species makes local averages ill-defined since there is no dynamical mechanism which keeps local accumulation of matter within specific margins.
The way out commences from the theory of boundedness. At first let me present how the major assumptions of that theory help to formally derive the Poisson distribution and then, in the next section I will present the major dynamical mechanism for controlling growth of the local fluctuations.
Let me start with the fact that under boundedness, each and every bounded irregular sequence (BIS) has well defined mean and variance according to the Lindeberg theorem [2] . On the grounds of this fact I suggest that the coarse-grained structure of each and every BIS consists of excursions of specific duration and amplitude. An exclusive for the boundedness property is that each excursion is embedded in a specific for it interval, called embedding time interval, so that no other excursions of larger size can be found in that interval. The role of embedding is to prevent overlapping of successive excursions and thus to sustain boundedness of rates and amplitudes. This result can be found in Chapter 5 of the book [6] . Further, it is proven that the excursions form a homogeneous process and thus successive excursions turns uncorrelated. It is worth noting that on fine-grained level there are correlations among successive excursions because the successive steps that built any given excursion are subject to boundedness of rates and amplitudes.
The statistical independence of different excursions makes possible to conclude that every local average is subject to the following estimation:
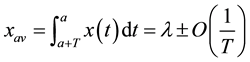 (2)
(2)
where T is the length of the time window and 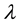 is the mean. Equation (2) implies that the deviation of the local average from the mean is inversely proportional to the length of the time window. This estimation is grounded on the fact that the characteristics of every excursion are independent from length of the time window. Thus, the number of excursions participating in the time window is proportional to its length which yields the local average to follow Equation (2). Then, Equation (2) stands as a necessary and sufficient condition for the following estimation to hold:
is the mean. Equation (2) implies that the deviation of the local average from the mean is inversely proportional to the length of the time window. This estimation is grounded on the fact that the characteristics of every excursion are independent from length of the time window. Thus, the number of excursions participating in the time window is proportional to its length which yields the local average to follow Equation (2). Then, Equation (2) stands as a necessary and sufficient condition for the following estimation to hold:
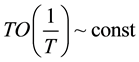 (3)
(3)
The meaning of Equation (3) is as follows: given the elementary event to be the deviation of a local average
in any moment from the mean; according to Equation (2) its probability is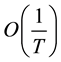 . Then Equation (3) gives the
. Then Equation (3) gives the
necessary for the derivation of the Poisson distribution relation between the number of trials T and the probability for the event in a single trial. An exclusive property of Equation (3) is that it is exact relation and it does not impose any special conditions on neither of the variables involved. Thus, the necessary and sufficient condition for the derivation of the Poisson distribution is met. It is worth noting that the present derivation of the Poisson distribution is free from any special conditions apart from the constraints which boundedness imposes in general.
Moreover, its enormous advantage is that the derivation is free from any constraint imposed over the size of the window T. Alongside, the derivation is free from any dependence on the specific size which specific pro- cesses imposed on any given system. In turn this renders the notion of concentration well-defined in each and every point of the system and in every moment.
4. Dynamical Mechanism for Controlling Local Accumulation of Matter/Energy
The major goal of the present section is to present the dynamical mechanism which controls unrestrained growth of local accumulation of matter/energy/information. Detailed description of this mechanism can be found in Chapter 3 of [6] . I present it here because a certain result is obtained here as a consequence of the derivation made in [6] .
As it has been already stated in the Introduction, the boundedness over velocities alone is not sufficient to ensure automatic damping of the fluctuations. This is so because the traditional approach to interactions assumes interactions among colliding species to be unitary. The latter implies that a certain number of colliding species form a closed system during interaction. In turn, the unitarity of the interactions renders mutual independency of the properties of different species. Consequently the latter validates the Law of Large Numbers which says that the one can assign probability to a given event which is given by the average of many independent events. However, there is a flaw: being independent from one another, prior to averaging, large enough fluctuations can cause severe damages on each and every system such as pattern formation, sintering, overheating, ageing etc. In any case, the lack of a uniform convergence makes a system to behave in an uncontrolled and non-reproducible way.
In Chapter 3 of [6] I have proposed the way out from the above problem. It assumes that along with the unitary interactions there are non-unitary ones whose role is to dissipate the accumulated energy and matter throughout a system so that to keep local concentrations bounded.
An exclusive generic property of a non-unitary interaction is that its time asymmetry renders each and every such interaction dissipative. Indeed, the time asymmetry renders the asymmetric role of any species that is as follows: the impact of the i-th species on the j-th one does not turn out equal to the impact of j-th species on the i-th one because we have to take into account the non-equal impact on each of them by a third species entering the collision. Thereby the corresponding Hamiltonian turns always into non-Hermitian (its eigenvalues are complex numbers), hence dissipative. On the other hand, we look for a mechanism able to “disperse” every locally accumulated by unitary interactions energy/matter. And namely the generic dissipativity of the non-unitary interactions is a key ingredient of that mechanism. The next step is to establish how the dissipated by a non-unitary interaction energy becomes dispersed throughout the corresponding system. I assume that it happens as follows: the dissipated from non-unitary interaction energy resonantly activates an appropriate local linearly-dispersed gapless mode (e.g. acoustic phonon) of the corresponding state variable (e.g. concentration), by means of which “dispersion” of the accumulated matter over the entire system is achieved. Further, the need for stable and reproducible functioning of a system imposes the following general requirement to the operation of that feedback: it must provide those fluctuations covariant, i.e. it must provide independence of the characteristics of each and every of them from their location and moments of their development.
The concept of boundedness, applied to the operation of the above feedback, implies that it must maintain stability by means of providing the effect of each and every interaction to be always bounded. This implies that whatever the specific characteristics of any given non-unitary interaction are, the operation of the feedback is such that the effect over each and every of the colliding species is finite and bounded. This property delineates the fundamental difference between a unitary and a non-unitary interaction. Indeed, whilst the unitaritity implies linearity and additivity of the corresponding interactions at the expense of allowing arbitrary accumulation of matter/energy, the boundedness applied to non-unitarity keeps the effect of any interaction bounded at the expense of introducing non-linearity and non-additivity of its execution. Consequently, the non-unitary interactions acquire the following 3 generic properties imposed by the boundedness:
1) The Hamiltonian of a non-unitary interaction is described by a non-symmetric random matrix of bounded elements. The property of being random is to be associated with the interruption of an unitary collision by another species at a random moment; and since the original distance to the interrupting species is of no importance for any given collision, a non-unitary interaction is not specifiable by metric properties such as the distance between species―it is rather specifiable by the correlations among the interacting species so that the intensity of these correlations are permanently kept bounded within metric-free margins.
2) The requisition about limited effect of the interactions over each participating species is further substantiated by setting the wave-functions to be bounded irregular sequences (BIS). Indeed, an exclusive property of the BIS’s is that each one is orthogonal to any other; alongside, each of them is orthogonal to its time and spatial derivatives. The latter property is crucial for providing the covariance of the non-unitary interactions since: (i) the orthogonality of every BIS to its spatial and time derivatives provides independence of each and every non- unitary interaction from the interaction path of any participating species; in turn, the obtained independence renders every non-unitary interaction a local event, that is: it depends on current status of participating species only; (ii) alongside, the orthonormality of the BIS`s renders the probability for finding a species independent from its current position, and from the position of its neighbors.
3) In order to keep the effect of non-unitary interactions permanently bounded and covariant, I suggest that the transitions introduced by them are to be described by operations of coarse-graining. To remind, the coarse- graining is mathematical operation which acts non-linearly and non-homogeneously on the members of BIS under the mild constraint of maintaining their permanent boundedness alone. As discussed in Chapter 1 of the book [6] , this makes a set of BIS’s dense transitive set where the coarse-graining appears to be an operation that transforms one BIS into another. Thus, the self- consistency of the frame is achieved: the eigenfunctions are supposed always to be BIS and the transitions described as operations of coarse-graining sustain that property since an operation of coarse graining transforms one BIS into another.
Further in Chapter 3 of [6] it is proven that the eigenvalues of any bounded non-Hermitian Hamiltonian tend to cluster near unit circle and their angles are uniformly distributed. The clustering of the eigenvalues at the unit circle provides not only boundedness of the amplitude of each fluctuation but boundedness of the rate of development of a fluctuation. Indeed, the rate of a fluctuation is given by the real part of any eigenvalue and thus it is not only bounded but covariant as well; alongside the corresponding rate of its development is given by
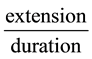 ; the duration is given by the imaginary part of the corresponding eigenvalue
; the duration is given by the imaginary part of the corresponding eigenvalue 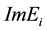 and its spatial
and its spatial
extension is also related to the imaginary part of the same eigenvalue trough the dispersion relation of the excited mode; since it is assumed that the feedback operates through excitation of linearly dispersed gapless modes
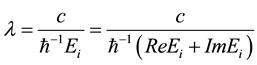 ; thus the extension length is
; thus the extension length is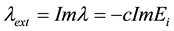 ; thereby the rate of development
; thereby the rate of development  is proportional to the velocity of the acoustic phonons . Note that the independence of the rate
is proportional to the velocity of the acoustic phonons . Note that the independence of the rate
of development from the size of the fluctuation, from the particularities of the interactions and from the moment and location of its development renders its covariance.
The generalization of the above presented results reads that there exists natural mechanism for maintaining the stability of a system by means of permanent preventing accumulation of arbitrary large amount of matter and energy. The presence of non-unitary interactions along with linearly dispersed gapless modes such as acoustic phonons in every many-body system renders the feedback universally available. We have proved that the operation of that mechanism under boundedness renders fluctuations covariant, extended to bounded size both in space and in time objects which appear, develop and relax with bounded rate.
It is an immediate consequence of the above considerations that the relative velocity of the species involved in a fluctuation is also constant and thus neither molecule is accelerated or retarded during relaxation. Indeed, it is obvious that the rate of dispersion is sustained bounded if and only if the dissipative energy is kept on the unit circle; if otherwise, the gradual dispersion of energy would provide permanent acceleration of species that take
part into each fluctuation; it is best seen by the permanent increase of the rate of dispersion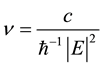 . In turn,
. In turn,
this destabilizes the corresponding system and yields its explosion. Along with heating up, there would be an accelerating expansion of the particles that participate to each fluctuation. Indeed, the current velocity of each molecule is:
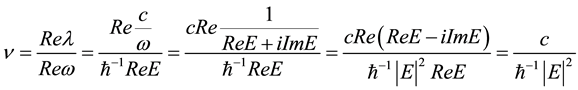
In consequence any decrease of 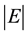
Outlining, it is proven that the necessary and sufficient conditions for providing covariance of the macroscopic thermodynamical variables such as temperature and concentration render constant relative velocity among species which does not change under damping of fluctuations.
5. Conclusion
In the present paper, I have demonstrated that the intensive macroscopic variables such as temperature and concentration are well-defined even for structured objects such as living organisms and for nano-objects. The proof is made under the mild assumptions of the concept of boundedness. No special additional conditions are necessary for it. In the course of the proof it turns out that the Poisson distribution turns ubiquitous for the description of the deviations from the mean. An indispensable part of the proof is the existence of a general dynamical mechanism which provides damping out of the arbitrary accumulation of matter/energy in every given location and in every moment. Thus, the dynamical mechanism serves as an implement for sustaining boundedness of the rates and amplitudes of the local fluctuations.
Cite this paper
Maria K.Koleva, (2015) Temperature and Concentration under Boundedness. Journal of Modern Physics,06,1149-1155. doi: 10.4236/jmp.2015.68118
References
- 1. Nicolis, G. and Prigogine, I. (1977) Self-Organization in Non-Equilibrium Systems. Wiley, New York.
- 2. Feller, W. (1970) An Introduction to Probability Theory and its Applications. John Willey & Sons, New-York.
- 3. Montroll, E.W. and. Schlesinger, M.F. (1984) On the Wonderful World of Random Walks. In: Lebovitz, J. and Montroll, E., Eds., Studies in Statistical Mechanics, v.11, North-Holland, Amsterdam, 1.
- 4. Koleva, M.K. (2006) Self-Organization and Finite Velocity of Transmitting Substance/Energy through Space-Time. arXiv:nlin/061048
- 5. Koleva, M.K. and Covachev, V. (2001) Fluctuation and Noise Letters, 1, R131-R149.
http://dx.doi.org/10.1142/S0219477501000287 - 6. Koleva, M.K. (2012) Boundedeness and Self-Organized Semantics: Theory and Applications. IGI-Global, Hershey, PA.
- 7. Schuster, H.G. (1984) Deterministic Chaos: An Introduction. Physik-Verlag, Weinheim.
- 8. Bak, P., Tang, C. and Wiesenfeld, K. (1987) Physical Review Letters, 59, 381-384.
http://dx.doi.org/10.1103/PhysRevLett.59.381

