Journal of Modern Physics
Vol.06 No.07(2015), Article ID:57675,9 pages
10.4236/jmp.2015.67101
The Physical Metric and Compact Objects
Yukio Tomozawa
Michigan Center for Theoretical Physics and Randall Laboratory of Physics, University of Michigan, Ann Arbor, MI, USA
Email: tomozawa@umich.edu
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 April 2015; accepted 27 June 2015; published 30 June 2015
ABSTRACT
In the previous work, the author introduces the physical metric for spherically symmetric and static metric which satisfies all the experimental tests of general relativity. This metric changes the nature of gravity for compact objects, such as black holes and neutron stars. It introduces the extended horizon which is 2.60 times of the Schwarzschild radius and plays a determinant role in the size of compact objects. This provides the prediction that the gravitational red shift z on the surface of compact objects is universal value of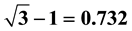 . None of the observed neutron stars rotate fast enough to change this prediction significantly. The gravity inside the extended horizon is repulsive. The effect of this repulsive force causes supernova explosion, high energy cosmic ray generation from AGN and explains the acceleration of the universe expansion.
. None of the observed neutron stars rotate fast enough to change this prediction significantly. The gravity inside the extended horizon is repulsive. The effect of this repulsive force causes supernova explosion, high energy cosmic ray generation from AGN and explains the acceleration of the universe expansion.
Keywords:
Compact Objects, Black Holes, Neutron Stars, Physical Metric, Gravitational Red Shift

1. Introduction
The Schwarzschild metric is the exact solution for the Einstein Equation of general relativity. However, it has been shown that by analyzing the geodesic equation, the time delay experiment data [1] [2] , by Shapiro et al., is not correctly explained by the Schwarzschild metric. The metric that fits all the experimental data has been suggested by the author and is called the physical metric [3] . It is a coordinate transformation of the Schwarz- schild metric, and it yields a significantly different picture of gravity. In particular, the description of compact objects, such as black holes and neutron stars, based on the physical metric presents a dramatic change in the understanding of gravity. In Section 2, the physical metric is introduced from the author’s previous work [3] . The extended horizon and its impact on the size of compact objects are discussed in Section 3. In Section 4, the Kerr metric for compact objects with charge and rotation is introduced and the extended horizon is described as the size of the compact objects. The discussion of the size and gravitational red shift on the surface for neutron stars is presented in Section 5. Here, the universal value for gravitational red shift on the surface is calculated, which is applied to all compact objects, unless the rotation is close to the critical frequency. This will be a crucial constraint for the forseeable future, since all the observed rotations of neutron stars are far from the critical frequency. Section 6 deals with supernova explosion and cosmic ray generation from AGN (Active Galactic Nuclei) as a natural outcome of repulsive force inside the extended horizon. In Section 7, the acce- leration of the universe expansion is also the result of the same repulsive force inside the extended horizon. The details of the discussion on this subject will follow in an upcoming paper. Section 8 is the summary and discussion.
2. The Physical Metric
The spherically symmetric and static (SSS) metric is expressed as
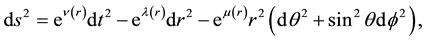 (1)
(1)
for a mass point M. From the fact that the transformation, 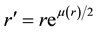 , leads to the Schwarzschild metric, one can deduce the expression for the metric,
, leads to the Schwarzschild metric, one can deduce the expression for the metric,
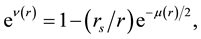 (2)
(2)
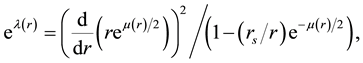 (3)
(3)
where 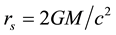 is the Schwarzschild radius. An asymptotic expansion for the metric functions can be obtained from Equation (2) and Equation (3), yielding
is the Schwarzschild radius. An asymptotic expansion for the metric functions can be obtained from Equation (2) and Equation (3), yielding
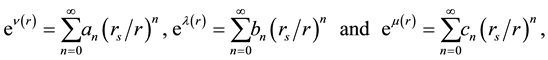 (4)
(4)
where
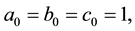 (5)
(5)
 (6)
(6)
and
 (7)
(7)
It is obvious that 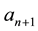 and
and  can be expressed as functions of
can be expressed as functions of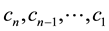 .
.
Using the geodesic equation, the author has concluded that all the existing experimental data of general relativity can be fitted by the metric satisfying the condition
 (8)
(8)
while the Schwarzschild metric fails to fit the data of time delay experiment of Shapiro et al. [1] [2] . The author called the metric that fits the time delay experiment data the physical metric [3] . It is a metric in which the speed of light on the spherical direction is equal to that in vacuum. It is interesting to observe that the speed of light in the direction perpendicular to the direction of the gravity is not effected from the value in vacuum in the physical metric and only such a metric satisfies the experimental data. Writing
 (9)
(9)
one gets for the asymptotic solution,
 (10)
(10)
Then one has

or

Differentiating Equation (12), one gets

From Equation (3), the metric function in the radial direction can be calculated

The asymptotic expansion of the metric functions can be calculated from Equation (11), Equation (12) and Equation (14) as

and

From Equation (11) or Equation (12), it is clear that one covers the range of

and

In order to cover the range of

one has to use non-asymptotic solution of the Schwarzschild solution,

and

where A and D are constants. Then, the metric functions for the physical metric in the region

are expressed as

and

and hence

or

Differentiating Equation (25), one gets

and

Imposing the continuity of the asymptotic expression, Equation (11) and the non-asymptotic expression, Equation (25) at

one gets

The most appropriate region in the parameter space is

since the range of coordinate, r, is covered by the origin and the positivity of the metric functions are main- tained.
Figure 1 shows the picture of 

In the region of Equation (31), the distance r can be reached at zero when 


Notice that there is one undecided parameter which can be fixed for the physics inside the radius at

3. The Extended Horizon
At the radius


The speed of light in the radial direction is given by

in the asymptotic region and

in the non-asymptotic region. Since

and

Equation (36) and Equation (37) are positive definite except at the radius

where



while 

From the property of Equation (42), one may call the radius of Equation (40) the extended horizon. The passage of a particle through the extended horizon in and out is permissible. An important property of gravity is that inside the extended horizon the gravity is repulsive, as is seen from Figure 1 or from Equation (27). When a gravitational collapse happens for a massive star or a black hole, large amounts of matter go into the inside region of the extended horizon. Then the gravity inside the extended horizon acts as a repulsive force to the entering matter and some of them are eventually expulsed from the extended horizon. This is the mechanism of supernova explosion or cosmic ray acceleration by AGN.
From Equation (13), the asymptotic solution outside the extended horizon behaves

This can be seen also from Figure 1. In other words, the gravitational force from the outside of the extended horizon is infinitely large. This indicates that the extended horizon gives a measure of the size of the objects. In the next section, the physical metric is extended to a mass with charge and rotation. There, it will be shown that the same conclusion will be given for the size of compact objects for a mass with charge and rotation.
4. The Metric with Charge and Rotation
The metric for a mass with charge and rotation is expressed as [4]

where the metric functions, 

in order to accommodate to the physical metric in the limit of no charge and no rotation. For the asymptotic region

or outside of the extended horizon, one gets




and

where a and Q are angular momentum per mass and charge parameter, respectively. Here, 

in Equation (11). In the limit of

these metric functions coincide with the physical metric in Section 2.
In order to find the gravitational force implied by this Kerr metric, let us compute

Here

becomes positive infinity at the extended horizon,

and the numerator of the coefficient of 

Then, the value of Equation (55) at the extended horizon becomes positive infinity if the condition

is satisfied. In such a case, the extended horizon behaves like a straight wall for a stable state. In that sense, the extended horizon gives the size of stable black hole or stable neutron star. Notice that the metric for a black hole and a neutron star is identical. When gravitational collapse happens for black hole or neutron star, then the repulsive force of gravity inside the extended horizon acts an agent to repel the collapsed objects to the outside the extended horizon. This is a new feature of a compact object, such as black hole or neutron star. It is very different from the description of the Schwarzschild metric framework.
5. The Size and Gravitational Red Shift of Neutron Star
For a standard mass of a neutron star,

the Schwarzschild radius is

and the extended horizon radius is

This is very close to the radius of a neutron star, estimated from the equation of state [5] - [7] . Since, however, the radius of the extended horizon is proportional to the mass, while the radius of a neutron star estimated from the equation of state is not proportional to the mass. If the determination of the mass and radius is obtained from the observation in the future, one can conclude which method will give the correct result.
Upon neglecting the rotation, the gravitational red shift on the surface of compact object can be determined by

or

This result is independent of the value of the mass of the object or independent of the nature of the compact object, neutron stars or black holes. This is a remarkable prediction for compact objects that needs to be tested in the future. The gravitational red shift for a rotating system can be computed as [8]

where the rotation parameter, 


For the value of Equation (62) for the extended horizon, one gets the critical frequency

or

None of the observed neutron stars rotate this fast. (The fastest rotation observed is 716 Hz for PSR J1748- 2446ad [9] .)
The gravitational red shift on the surface of neutron star, EXO 0748-676, in our galaxy, has been reported as [10]

and the mass of neutron star are estimated

On the other hand, the frequency X-ray pulsation of neutron star has been reported as [6]

and [7]

Since the correction of the rotation for the gravitational red shift is the second order, the correction factor of the rotation of Equation (72) is of the order of

Then, it is clear that the rotation of Equation (72) is not large enough to make a shift from non-rotational gravitational red shift of Equation (64) to the observed one, Equation (69), by a rotational effect. The effect of the rotation, Equation (71), is even smaller. In order to resolve the discrepancy, one has to conclude that either the observed gravitational red shift, Equation (69) is in error or there has to exist an unobserved faster rotation. It is important to make the observation of gravitational red shift from the surface of neutron stars and possibly from black holes on a large scale.
It should be emphasized that the prediction for the size and the gravitational red shift from the surface are identical to neutron stars and black holes. It is important to realize that neutron stars and black holes are the compact objects which belong to the same species from the concept of general relativity. The size of a black hole can be measured when the MIT Haystack Telescope [11] starts to operate. At that point, one can determine whether they can observe the radius of the extended horizon which is 2.60 times bigger than the Schwarzschild radius.
6. Supernova Explosion and Cosmic ray Generation from AGN
What is the cause of a supernova explosion? From the introduction of the physical metric, it is clear why it was exploded. When a gravitational collapse of a large star happens at the end of nuclear fusions, collapsed matter is subject to repulsive force of the gravity inside the extended horizon. The explosion of supernova is a realization of repulsive forces. All numerical simulation in the past should be repeated with the use of the physical metric The ad hoc introduction of repulsive elements in the numerical calculation is not necessary. The physical metric provides a natural mean of a repulsive agent automatically. One undecided parameter in the metric can be determined from numerical calculation and a comparison with the observed data.
The data of the Auger Observatory indicates some correlation between the source of high energy cosmic rays and the location of AGN [12] . AGN are massive black holes. Do massive black holes emit high energy cosmic rays? Not in the black hole framework based on the Schwarzschild metric. After having accepted the physical metric on the basis of black holes, it provides a new conceptual basis. When large amounts of matter fall into a massive black hole in a gravitational collapse, a process similar to supernova explosion takes place, and it is subject to repulsive forces inside the extended horizon. After reaching the central core of the black hole, the repulsive force acts upon to the collapsed matter. This results in an expansion of a heat bath, the surface of which plays the role of emission of particles, proton, electrons, neutrinos and any other particles. Only the rule of statistics decides the nature of composition of emitted particles. It is similar to the universe expansion. It was shown that for the expansion rate of the heat bath surface [13] ,

one gets the energy spectrum for the emitted particle.

Then, the energy spectrum above the knee energy, E-3, can be derived from the expansion rate of radiation- dominated expansion 

This idea of cosmic ray generation from AGN was proposed in 1985 by the present author [14] . Then, the author utilized the fact that quantum effects of fields on gravity gives a repulsive force at the center. This idea is replaced by a robust repulsive force of the physical metric. In the next section, the author applies the physical metric to cosmology and the repulsive force of the physical metric creates the acceleration of the universe ex- pansion. This cannot be achieved by the quantum effects on gravity in 1985. It is too small as an effect in cos- mology. One needs the robust repulsive force in the physical metric.
The transition from the radiation-dominated regime to the matter-dominated regime at energy at 3 PeV, as is observed in the cosmic ray energy spectrum, requires the existence of the new mass scale of 3 PeV. This indicates new physics at 3 PeV. Assuming supersymmetric theory of GLMR [15] -RS [16] (Giudice-Luty- Murayama-Ratazzi, Randall-Sandrum), the lowest mass is estimated as 8 TeV for the highest mass of 3 PeV. Adding 8 spectra of the HESS data [17] , the author found a 3s bump at 8 TeV [18] . A further collection of the gamma ray data is recommended. A search for 3 PeV particle as the new mass scale for dark matter particles will be the next target of high energy physics. A possible new particle at 3 PeV is named as Cion, cosmic inter- face particle [13] . (The Chinese word for knee is Xi, pronounced as shi.)
7. Acceleration of Universe Expansion
Applying the physical metric to the expanding universe, we are inside the extended horizon of the universe. Then, the repulsive force inside the extended horizon accelerates anybody inside the extended horizon. Of course, one has to make a coordinate transformation to make a connection to the Friedman-Robertson-Walker (FRW) metric [4] for the expanding universe. I will address this in a future paper. I emphasize that the reason for dark energy should lies in the use of the physical metric. Since all the metric functions of the physical metric and the FRW metric are positive definite, one has natural means for appropriate coordinate transformation. Only the difference between the explanation by the physical metric and the dark energy is that in the former the acceleration terminates outside the extended horizon, while in the latter the acceleration is eternal. The author will present this work in the next article.
8. Summary
From the introduction of the physical metric, one encounters a revolutionary change in the feature of compact objects, black holes and neutron stars. The extended horizon, 2.60 times of that of the Schwarzschild radius, is the size of compact objects. The gravitational red shift on the surface of compact objects is the universal value of 0.732 except for the effect of rotation. This universal prediction is valid for any mass and any species, black holes or neutron stars. It is important to test this prediction extensively.
Acknowledgements
It is a great pleasure to thank Peter K. Tomozawa and Donna LeDuc for reading the manuscript.
References
- Shapiro, I.I., Ash, M.E. and Tausner, M.J. (1966) Physical Review Letters, 17, 933. http://dx.doi.org/10.1103/PhysRevLett.17.933 Resenberg, R.D. and Shapiro, I.I. (1979) Astrophysical Journal, 234, L219-L221. http://dx.doi.org/10.1086/183144
- Bertotti, B., Iess, L. and Tortora, P. (2003) Nature, 425, 374-376. http://dx.doi.org/10.1038/nature01997
- Tomoawa, Y. (2015) Journal of Modern Physics, 6, 335-345. http://dx.doi.org/10.4236/jmp.2015.63036
- Misner, C.W., Thorne, K.S. and Wheeler, J.A. (1973) Gravitation. Freeman, San Francisco. Weinberg, S. (1972) Gravitation and Cosmology. Wiley and Sons, New York.
- Steiner, A.W., Lattimer, J.M. and Brown, E.F. (2010) The Astrophysical Journal, 722, 33. http://dx.doi.org/10.1088/0004-637X/722/1/33
- Villarreal, A.R. and Strohmayer, T.E. (2004) The Astrophysical Journal, 614, L121. http://dx.doi.org/10.1086/425737
- Galloway, D.K., et al. (2010) The Astrophysical Journal, 711, L148-L151.
- Dubey, A.K. and Sen, A.K. (2014) Journal of Physics, Conference Series, 481, Article ID: 012010. http://dx.doi.org/10.1088/1742-6596/481/1/012010
- Hessels, J.W.T., Ransom, S.M., Stairs, I.H., Freire, P.C.C., Kaspi, V.M. and Camilo, F. (2006) Science, 311, 1901- 1904. http://dx.doi.org/10.1126/science.1123430
- Gottam, J., Paerels, F. and Mendez, M. (2002) Nature, 420, 51-54.
- Rogers, A.E.E., Barvainis, R., Charpentier, P.J. and Corey, B.E. (1993) IEEE Transactions on Antennas and Propagation, 41, 77-84. http://dx.doi.org/10.1109/8.210118
- The Pierre Auger Collaboration, Abraham, J., Abreu, P., Aglietta, M., Aguirre, C., Allard, D., Allekotte, I., et al. (2007) Science, 318, 938-943. http://dx.doi.org/10.1126/science.1151124
- Tomozawa, Y. (2013) Journal of Modern Physics, 4, 385-389. http://dx.doi.org/10.4236/jmp.2013.43054
- Tomozawa, Y. (1985) Magnetic Monopoles, Cosmic Rays and Quantum Gravity. Proceedings of the INS International Symposium on Composite Models of Quarks and Leptons, Tokyo, 13-15 August 1985, 386. Rays, C. (1986) Quantum Effects of Gravity and Gravitational Collapse. Proceedings of the Second Workshop on Funda- mental Physics, Humacao, 24-28 March 1986. This Lecture Note Can Be Retrieved by KEK Kiss No. 200035789.
- Giudice, G.F., Luty, M.A., Murayama, H. and Ratazzi, H.R. (1998) Journal of High Energy Physics, 12, 27.
- Randall, L. and Suundrum, R. (1999) Nuclear Physics B, 557, 79-118. http://dx.doi.org/10.1016/S0550-3213(99)00359-4
- Aharonian, F., Akhperjanian, A.G., de Almeida, U.B., Bazer-Bachi, A.R., Behera, B., Beilicke, M., et al. (2008) Astronomy and Astrophysics, 477, 353-363. http://dx.doi.org/10.1051/0004-6361:20078516
- Tomozawa, Y. (2010) Evidence for a Dark Matter Particle. arXiv:1002.1938



 , as a function of
, as a function of  in the SSS physical metric.
in the SSS physical metric.