Journal of Modern Physics
Vol.06 No.04(2015), Article ID:55010,8 pages
10.4236/jmp.2015.64050
The Stable Wave Packet in the Foundations of Quantum Mechanics
Antony J. Bourdillon
UHRL, San Jose, USA
Email: bourdillona@sbcglobal.net
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 February 2015; accepted 22 March 2015; published 25 March 2015
ABSTRACT
The stable wave packet has been missing in quantum mechanics for a long time. A consistent argument finds, in antimatter, regular group and phase velocities, along with negative energy and negative mass. For this, a new wave function is derived for free antiparticles, consistent with the Feynman-Stueckelberg switching principle. The wave packet, expressing internal periodicity together with external confinement, is ubiquitous in physics. The stable wave packet has many consequences, a few of which are mentioned. They extend to the debate about what is measurable in physics and to localization of quantized properties in entangled particles.
Keywords:
Stable Wave Packet, Travelling Wave Group, Negative Mass, Antimatter, Negative Energy, Quantum Mechanics, Wave Mechanics

1. Introduction
Following Dirac [1] , the wave packet is generally supposed unstable. However, the following travelling wave group for a free particle or photon,
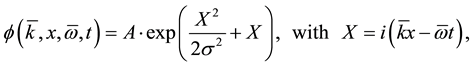 (1)
(1)
defined on values of mean wave vector
 and mean angular frequency
and mean angular frequency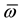 , is a stable wave packet. Those two variables are themselves stable not only because they are mean values in a symmetric wave function, but also because their stability is guaranteed by respective conservation of momentum and energy and triple guaranteed by symmetry in space-time. In one spatial dimension for simplicity, X is an imaginary variable that causes ϕ to oscillate. If the real part represents the electric field in an electromagnetic wave, the imaginary part represents its magnetic force field. The denominator σ is particular because it depends on initial conditions, but it is stable during propagation in free space as a consequence of Newton’s first law of motion. The normalizing amplitude A depends on σ and is therefore equally stable. The envelope, exp(X2/2σ2), depends on the square of imaginary X, a function of four variables. Two are already described, so we are left with the variables x and t that describe the profile. Since the other variables are all stable, this profile is also stable. With a stable wave group, we can progress to new physics. The one dimensional equation is easily extended to four space-time dimensions by appropriate substitution of the scalar product k×r for kx. Exceptional about this wave function is the fact that it is defined by mean values while also containing a continuous range of component energies and momenta that are accessible by Fourier transforms. The back transform on the Gaussian shows that these components are also stable (Appendix).
, is a stable wave packet. Those two variables are themselves stable not only because they are mean values in a symmetric wave function, but also because their stability is guaranteed by respective conservation of momentum and energy and triple guaranteed by symmetry in space-time. In one spatial dimension for simplicity, X is an imaginary variable that causes ϕ to oscillate. If the real part represents the electric field in an electromagnetic wave, the imaginary part represents its magnetic force field. The denominator σ is particular because it depends on initial conditions, but it is stable during propagation in free space as a consequence of Newton’s first law of motion. The normalizing amplitude A depends on σ and is therefore equally stable. The envelope, exp(X2/2σ2), depends on the square of imaginary X, a function of four variables. Two are already described, so we are left with the variables x and t that describe the profile. Since the other variables are all stable, this profile is also stable. With a stable wave group, we can progress to new physics. The one dimensional equation is easily extended to four space-time dimensions by appropriate substitution of the scalar product k×r for kx. Exceptional about this wave function is the fact that it is defined by mean values while also containing a continuous range of component energies and momenta that are accessible by Fourier transforms. The back transform on the Gaussian shows that these components are also stable (Appendix).
Some consequences are immediate; others require further input or supposition. We will consider them in antimatter, in mass, and in energy. In particular, we find a new interpretation for Dirac’s calculated negative energy states, which he modeled on hole behavior in semiconductor conduction bands. Those states are not universally favored [2] , but the new wave function offers a novel way for considering annihilation and creation in the context of negative energy and negative mass. The latter is not a new concept for elementary particles [3] , but with a new representation for the wave function of antiparticles, we also find a non-paradoxical explanation for the Feynman [4] -Stueckelburg [5] switching principle, “negative-energy objects travelling forward in time do not exist; any negative energy object P travelling backwards in time can and must be described as its anti object
 going in the opposite way in space, but endowed with positive energy and motion forward in time”. This principle, though stated to explain transition and scattering probabilities, seems to contradict cloud chamber and bubble chamber images of particle creation. The principle however can be shown consistent with our wave function for the antiparticle to the electron. There are further implications for symmetry, gravity, and yet wider reaches of physics. Some supporting detail has been previously described [6] - [8] . The summary examples are as follows: 1) simulations with Maxwell’s equations demonstrate that the group and phase velocities in a medium of refractive index n follow the relation
going in the opposite way in space, but endowed with positive energy and motion forward in time”. This principle, though stated to explain transition and scattering probabilities, seems to contradict cloud chamber and bubble chamber images of particle creation. The principle however can be shown consistent with our wave function for the antiparticle to the electron. There are further implications for symmetry, gravity, and yet wider reaches of physics. Some supporting detail has been previously described [6] - [8] . The summary examples are as follows: 1) simulations with Maxwell’s equations demonstrate that the group and phase velocities in a medium of refractive index n follow the relation
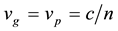 where n = 1 in vacuo where c is the speed of light; 2) locally, the wave packet travels faster than c in the deep X-ray spectral region where total external reflection occurs and is also near the fundamental edge in some ionic materials; 3) in electron-electron interactions, the phase can act as a hidden variable to determine the scattering angle and energy-loss in a single interaction; 4) in the stable wave packet, relativity implies a 5-dimesional space-time mass; 5) consistency requires the antiparticle to the electron to have negative mass with positive charge; 6) a graphic Hamiltonian to describe relativistic dynamics of an electron in magnetic fields is derived; 7) measurement of the stable wave packet is described as partly probabilistic and partly determined; 8) an inconsistency in the dynamics of Dirac’s positron is graphed, i.e. when his momentum k is equal to rest mass m0; 9) new conservation laws are described.
where n = 1 in vacuo where c is the speed of light; 2) locally, the wave packet travels faster than c in the deep X-ray spectral region where total external reflection occurs and is also near the fundamental edge in some ionic materials; 3) in electron-electron interactions, the phase can act as a hidden variable to determine the scattering angle and energy-loss in a single interaction; 4) in the stable wave packet, relativity implies a 5-dimesional space-time mass; 5) consistency requires the antiparticle to the electron to have negative mass with positive charge; 6) a graphic Hamiltonian to describe relativistic dynamics of an electron in magnetic fields is derived; 7) measurement of the stable wave packet is described as partly probabilistic and partly determined; 8) an inconsistency in the dynamics of Dirac’s positron is graphed, i.e. when his momentum k is equal to rest mass m0; 9) new conservation laws are described.
The stable wave group illustrates the fact that quantum mechanics is not just a series of microbangs or shrieks from Schroedinger’s cat, but the theory containing continuous transformations of wave functions where bound states are standing waves, and free particles are discussed. The travelling wave group is better suited to problems involving actions at a distance, including entanglement, than suited to close encounters where matrix methods are normally employed [9] . Meanwhile, both this theory and the Dirac theory are single particle models, but multi-particle collisions are made among single particles. So, the models remain relevant.
2. Immediate Consequences
Equation (1) is a solution to the wave equation (Appendix). The probability distributions
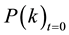 and
and
 are derived from Equation (1) by Fourier transforms. From them, the Uncertainty Principle is developed by using obvious, half-height-full-width definitions for the uncertainties
are derived from Equation (1) by Fourier transforms. From them, the Uncertainty Principle is developed by using obvious, half-height-full-width definitions for the uncertainties , where p represents momentum and v frequency. For the limited case of the free particle, quantum physics is therefore made a product of wave motion. From the equation are also derived for the case of the free particle, Planck’s law, the de Broglie hypothesis, and several conservation rules. Furthermore, operation of the relativistic Kline-Gordon equation on Equation (1) yields, as output for a particle in free space, an algebraic equation in second order:
, where p represents momentum and v frequency. For the limited case of the free particle, quantum physics is therefore made a product of wave motion. From the equation are also derived for the case of the free particle, Planck’s law, the de Broglie hypothesis, and several conservation rules. Furthermore, operation of the relativistic Kline-Gordon equation on Equation (1) yields, as output for a particle in free space, an algebraic equation in second order:
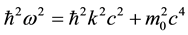 (2)
(2)
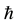 being the reduced Planck constant and c the speed of light. This is the same equation as is obtained from Einstein’s well known relativistic formula by substituting for energy
being the reduced Planck constant and c the speed of light. This is the same equation as is obtained from Einstein’s well known relativistic formula by substituting for energy
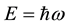 and for momentum
and for momentum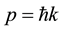 . The equation can be simplified with appropriate units
. The equation can be simplified with appropriate units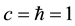 . Differentiation then gives a new result in relativity, for the product of group velocity1 vg and phase velocity vp:
. Differentiation then gives a new result in relativity, for the product of group velocity1 vg and phase velocity vp:
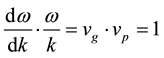 (3)
(3)
This result is plotted in the positive quadrants of Figure 1(b) for the case of rest mass m0 = 1. The group velocity is well behaved: it tends to zero at low k; to c at large k; and is relativistic elsewhere. It differs from Dirac’s calculation for the speed of the electron: he found it was equal to c. He knew this value to be unphysical but he “zitterbewegunged” in an unclear way. The speed of light is the geometric mean of the group and phase velocities. The phase velocity, w/k, brings clarity―what is it? It breaks the light barrier. Can it be measured? Yes, as the inverse of the group velocity. Again yes, as the ratio of energy to momentum. The operators for these two observables commute. But is the phase velocity real? No, it carries no energy; it is complex: it carries phase. Energy depends on the square of the wave modulus, the group profile. Notice that peaks in the carrier wave ? whether real or imaginary―appear, grow, pass through the wave group, and disappear, as though elastic.
Return to the algebraic Equation (2). Being second order, it has more than one solution. Dirac gave his negative eigenvalue to the positron and insisted that it has positive mass and positive kinetic energy. We suppose that the assignment of negative energy is correct because the opposite alternative is void as an explanation. However, when analyzing the velocities, a singularity appears when his k = m0, and this would give rise to unphysical results. In particular, the group velocity would break the light barrier and would extend to infinity; while the phase velocity would fall to zero [6] . Besides being unphysical in relativity, there is no experimental evidence for such features, so we return to basics. In first order, relativity gives E = mc2, where m is now relativistic mass. Therefore, E < 0 implies m0 < 0. Likewise, since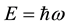 , then w < 0. Meanwhile, if w < 0 then k < 0, otherwise ϕ would decay, breaking conservation rules. These consequences are plotted consistently in the third quadrant in Figure 1(a). This shows how the representation―using positive and negative values for energy and momentum―can be used in new ways, notably in the center of mass frame. For example, vectorial subtraction of the two arrows shown, gives the net increase in absolute momentum that accompanies particle pair annihilation into two photons; while absolute energy is conserved in the vertical separation between the arrows. Moreover, in annihilation, two complex wave functions, representing a particle and its anti-particle, transform in the center of mass frame, to a real wave function, whose real and imaginary components are out of phase in the resultant electromagnetic wave: the superposition of the mass disturbances is consistent with the figure because
, then w < 0. Meanwhile, if w < 0 then k < 0, otherwise ϕ would decay, breaking conservation rules. These consequences are plotted consistently in the third quadrant in Figure 1(a). This shows how the representation―using positive and negative values for energy and momentum―can be used in new ways, notably in the center of mass frame. For example, vectorial subtraction of the two arrows shown, gives the net increase in absolute momentum that accompanies particle pair annihilation into two photons; while absolute energy is conserved in the vertical separation between the arrows. Moreover, in annihilation, two complex wave functions, representing a particle and its anti-particle, transform in the center of mass frame, to a real wave function, whose real and imaginary components are out of phase in the resultant electromagnetic wave: the superposition of the mass disturbances is consistent with the figure because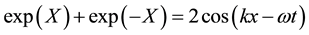 , a real value2.
, a real value2.
Further detail for the antiparticle is derived and listed in Table 1. Here chief novelties are those illustrated in Figure 1. The stable wave packet gives clarity to many opaque features in quantum mechanics: the rest mass energy of the positron is made negative, like its eigenvalue; the unphysical singularity at

1Since



2The photon electric field is a real wave function; the fermionic function is complex.
The stable wave packet has provided kinetics that contain, through application of negative mass, new symmetries―including the inversion symmetry about the origin in Figure 1(a)―and new conservation rules, listed in Table 1. Notice in particular the new symmetries that apply in pair annihilation and creation. We now examine the kinetics of particles accelerated in electromagnetic fields. The wave packet may then deform, but the general features in the free particle or antiparticle are retained by assumption. In particular, we seek a representation that conforms to the symmetries already described: for example, when an electric field is switched on, the absolute energy




Figure 1. (a) Solutions to Equation (2),

law of motion, since both would accelerate in the same direction, owing partly to the negative mass). The complication, involved in applying absolute mass to electromagnetic interactions in negatively massive antiparticles, may prove significant in future understanding of electronic charge.
A more significant consequence for the analysis displayed in Figure 1 is the negative energy states with w < 0. Dirac compared them to hole states in semiconductor conduction bands, where the holes exist as vacancies inside filled bands. These bands have normal gravitational properties in the semiconductor; but not in antiparticle space. They are therefore problematic. However the representation in the figure is consistent with the gravitation, while accounting for Dirac’s negative energy through the new combination of negative mass, negative kinetic energy, and negative momentum.
Table 1. Kinetics for the electron compared with the regular kinetics of the antiparticle a+, as derived from the stable wave packet; and with the singularity for Dirac’s positron, as described in the text. With the antiparticle a+, summed mass

“*m” is negative in antiparticles; **Feynman Stueckelberg principle; h' = h/2π; ***subscript i means sum over particles and antiparticles; **** e(−e) = −e2.
More generally, the wave packet that is newly described here is a common object in physics, especially wherever a particle is extracted from a Fermi sea or condensed phase. The wave packet describes, out of a great many examples, the photoelectron that resonates between neighboring atoms [10] in extended X-ray absorption fine structure; as it does the electrons or photons that are transmitted in the various kinds of microscope; and as it describes most interactions between particles or photons with matter. All are in fact energy quantized. The quantization is an additional extraneous constraint, because the concept of the wave packet does not necessarily imply quantization, though the packet is the necessary vehicle for the quantized photon or particle.
3. Further Consequences
3.1. Reasons for Reinterpreting Dirac Theory
Principal differences between consequences of the stable wave packet and Dirac’s theory are described in the previous paragraphs and summarized in the next. In contrast, the stable wave packet provides a consistent description for the kinetics of both the electron and its antiparticle.
・ He wrote mistakenly that the wave packet is unstable.
・ His calculation for the electron velocity, v = c, is unphysical: his result is the geometric mean of the group and phase velocities, as derived from the stable wave packet.
・ He ascribed negative energy with positive mass for the positron. This is contradictory for the kinetics of a slow antiparticle, though electromagnetic fields add a complication.
・ With positive kinetic energy, there is an unphysical singularity in vg and vp when k = m0. At this condition the positron passes through infinite relativistic mass.
There are many other inconsistencies and new applications that the stable wave packet can be used to resolve. Some are outlined in preliminary form in the following sections, to indicate both the broader view and as pointers to further research.
3.2. The Switching Principle
The packet allows a simple explanation for the Feynman-Stueckelburg switching principle, while being conventional in its general description of negative energy states. In Feynman diagrams, the principle corresponds to reversals of arrows that represent antiparticles. This is illustrated in a comparison of the Feynman diagrams in Figure 2(a) for electron Compton scattering [11] with Figure 2(b) for pair annihilation. Partial transition probabilities corresponding to these two channels are equivalent [12] . Likewise Figure 2(c) represents pair creation from a single gamma ray. This figure assumes the gamma ray has sufficient energy. These are all single channels that contribute to total scattering cross-sections. As is well known, corresponding laboratory frame diagrams are different. Figure 2(d) shows deflections through a magnetic field B, out of the plane. The electron and its antiparticle are deflected in opposing directions, having opposite charge. The laboratory frame diagrams in Figure 2(e) [2] and 2d compare respectively with Figure 2(b) and Figure 2(c). They illustrate the different purposes described for the Feynman diagrams, which are topological, and for scattering images, as observed in track images. The figure is consistent with our antiparticle wave function since the wave vector k for the antiparticle points in the opposite direction to its group velocity vg. Figure 1 shows that while the antiparticle momentum is negative; its group velocity is positive, as observed in cloud chamber and bubble chamber images. The arrows in the Feynman diagrams are charge conserving. Of course k is a vector and may be positive or negative, but


Figure 2. (a) The vertex for the Feynman diagram for electron Compton scattering [11] has the same scattering matrix element as the vertices in (b) for pair annihilation and (c) for pair creation. (e) and (f), in the laboratory frame, correspond to b and c respectively. Figure 2(d) illustrates deflections in a magnetic field with magnetic force field B directed out of the plane. The arrows in the Feynman diagrams signify phase properties; the laboratory frame group properties. They are both represented in the stable wave packet for an antiparticle.
3.3. Newtonian Time within a Wave Packet
Figure 1(b) showed how the particle phase velocity, which is always greater than c, tends to infinity as k tends to zero. This has special implications for a three (spatial) dimensional wave packet. In the plane normal to particle motion the crest of a wave front is continuous in Newtonian time. In consequence, a phase that is destroyed by interference at one point will be enhanced instantaneously at another and this peculiar type of information is transmitted at infinite speed. This is a startling proposition, but implicit in the fundamental equation of the stable wave packet. It also seems consistent with Bohr’s notion of the wholeness of a measurement [13] -[15] . But the proposition is limited to phase information within a wave group of matter3, in a frame where it has low kinetic energy. In the direction of propagation, time is relativisitic.
Likewise, in massless photons in free space, vp and vg have equal values c [8] . But the hitherto undiscovered stable wave packet is an undocumented feature in the analysis of entanglement at a distance, especially when experiments that use laser beams are involved. Then wave-vector line-widths can be narrow and packet lengths proportionately long. Each wave packet contains one particle or photon. Wave packets superpose
3.4. Entanglement at a Distance
The stable wave packet therefore provides new options for understanding entanglement at a distance. This has been demonstrated in many ways in both atomic and solid state physics [16] -[20] . The concept has been debated for a long time since Einstein, Podolski and Rosen claimed that their thought experiment proved quantum mechanics incomplete. Evidently, all information is not destroyed in measurement on the first particle, and some of it can be recovered elsewhere, at a later time, on the second particle. Notice that the description of entanglement by means of environmental factors has the same logic as the dispersion free, hidden variable that we find in the phase and velocity of the carrier wave. But the localization of information in a transported particle is now known to be consistent with experiment [17] -[19] and, contrary to Bohr’s view. The localization is also consistent with our concept of the carrier wave and stable wave packet.
4. Conclusion
Fundamental changes yield surprising results, here limited to free particles especially when viewed at a distance. The travelling wave group, based on mean values of a symmetric wave function, is shown to be a stable wave packet. Analysis of its kinetics is regular if the mass of the antiparticle is negative. Then the Feynman-Stueck- elberg switching principle is given a simple explanation. However, electromagnetic interactions are consistent if the effective mass (force/acceleration) is positive in both particles and antiparticles; but more generally, the kinetic implications of negative mass, as calculated in the free antiparticle, surely extend to the accelerated one where the wave packet deforms. The wave packet, newly described here in ideal, symmetric, and stable form, is the most common object that is observed in free particles. Since the stable wave packet contains information that is not present in the quantum mechanical wave function, this is incomplete. We conclude, with Einstein, Podolski and Rosen [20] that quantum mechanics is not complete.
References
- Dirac, P.A.M. (1958) The Principles of Quantum Mechanics. 4th Edition, OUP, Oxford.
- Charlton, M. and Humbertson, J.W. (2001) Positron Physics. CUP, Cambridge.
- Recami, E. and Ziino, G. (1976) Il Nuovo Cimento A series 11, 33, 205-215.
- Feynman, R.P. (1949) Physical Review, 76, 749-769. http://dx.doi.org/10.1103/PhysRev.76.749
- Stueckelberg, E.C.G. (1941) Helvetica Physica Acta, 14, 588-594.
- Bourdillon, A.J. (2014) Journal of Modern Physics, 5, 23-28. http://dx.doi.org/10.4236/jmp.2014.51004
- Bourdillon, A.J. (2013) Journal of Modern Physics, 4, 705-711. http://dx.doi.org/10.4236/jmp.2013.46097
- Bourdillon, A.J. (2012) Journal of Modern Physics, 3, 290-296. http://dx.doi.org/10.4236/jmp.2012.33041
- Feynman, R.P. (1949) Physical Review, 76, 769-789. http://dx.doi.org/10.1103/PhysRev.76.769
- Bourdillon, A.J., Pettifer, R.F. and Marseglia, E.A. (1979) Journal of Physics C, IOPP, 12, 3889-3897.
- Bourdillon, A.J., Brydson, R.D. and Williams, B.G. (1987) Journal of Microscopy, 145, 293-300.
- Ziman, J.M. (1969) Elements of Advanced Quantum Theory. CUP, Cambridge.
- As an Example of the Discussion, See Quantum Physics Entanglement Documentary―Atomic Physics Reality, 2014, Video by Ray Muon Published in Youtube, https://www.youtube.com/watch?v=BFvJOZ51tmc
- Pais, A. (1991) Niels Bohr’s Times in Physics, Philosophy and Polity. Clarendon, Oxford.
- Bohr, N. (1987) Philosophical Writings of Niels Bohr. Oxbow Press, Woodbridge, CT.
- Longdell, J. (2011) Nature, 469, 475-476. http://dx.doi.org/10.1038/469475a
- Aspect, A., Dalibard, J. and Roger, G. (1982) Physical Review Letters, 49, 1804-1807. http://dx.doi.org/10.1103/PhysRevLett.49.1804
- Aspect, A., Grangier, P. and Roger, G. (1982) Physical Review Letters, 49, 91-94.
- Aspect, A., Dalibard, J. and Roger, G. (1982) Physical Review Letters, 49, 1804-1807.
- Einstein, A., Podolski, B. and Rosen, N. (1935) Physical Review, 47, 777-780.
Appendix
A.1. Solution to the Wave Equation
The fact that the packet described in Equation (1) is stable followed from its dependence on the mean values


The former question is easily resolved, but the solution is enlightening and is given in outline. Begin by taking the second derivative of Equation (1) with respect to x at constant time t = 0:

Multiply by

Now compare this equation with


A.2. Fourier Transforms for the Uncertainty Principle
To express the variables w and k in the equation, find the Fourier transform F for the wave group, write:

Evaluating to:

where the back transform yields the original

In three spatial dimensions these equations are readily expanded. For example, since by normalization in one
dimension x,


NOTES
3For light in vacuo, phase velocities and group velocities have the same value, c [8] .





