Journal of Modern Physics
Vol.06 No.03(2015), Article ID:54306,10 pages
10.4236/jmp.2015.63036
Experimental Test of General Relativity and the Physical Metric
Yukio Tomozawa
Michigan Center for Theoretical Physics, Randall Laboratory of Physics, University of Michigan, Ann Arbor, USA
Email: tomozawa@umich.edu
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 February 2015; accepted 25 February 2015; published 28 February 2015
ABSTRACT
The author will show that neither the Schwarzschild metric nor the metric introduced in 1916 by Schwarzschild describes the data produced by the time delay experiment by Shapiro et al. The author will describe the physical metric that will explain the time delay experiment data correctly as a solution to Einstein Equation of General Relativity. Other tests of General Relativity, the bending of light, the advancement of perihelia, gravitational red shift and gravitational lensing are satisfied by both the Schwarzschild metric and author’s physical metric.
Keywords:
Time Delay Experiment, General Relativity, Physical Metric

1. Introduction
The Schwarzschild metric is the exact solution for the Einstein Equation of General Relativity. However, it will be shown that by analyzing the geodesic equation, the time delay experiment data, by Shapiro et al., is not completely explained by the Schwarzschild metric. The correction required to fit the data suggests a dramatic change in the direction of General Relativity and points to a new way of understanding the nature of gravity. The other tests of General Relativity, bending of light, advancement of perihelia, gravitational red shift and gravitational lensing, are well satisfied by the Schwarzschild metric as well as by author’s physical metric.
The structure of this article is as follows: First in Section 2, we derive the geodesic equation for the Spherically Symmetric and Static (SSS) metric. In Sections 3 and 4, we examine and apply the geodesic equation to the time delay experiment whereby one can conclude that the Schwarzschild metric does not fit the experiment. The author discusses the modification of the metric by a coordinate transformation which yields the physical metric that does fit the experiment in Sections 5 and 6. The physical metric dramatically changes the physical significance of gravity. The author expects that future experiments will further substantiate and differentiate the significance of the physical metric from that of the Schwarzschild metric. The implication of black holes based on the physical metric will be discussed in Section 7. The other tests of General Relativity are discussed in Section 8.
2. Asymptotic Form for the SSS Metric
The SSS metric is expressed as
 (1)
(1)
for a mass point M. From the fact that the transformation,  , leads to the Schwarzschild metric, one can deduce the expression for the metric,
, leads to the Schwarzschild metric, one can deduce the expression for the metric,
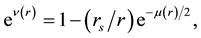 (2)
(2)
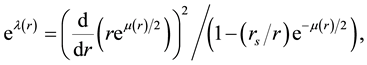 (3)
(3)
where  is the Schwarzschild radius. An asymptotic expansion for the metric functions can be obtained from Equation (2) and Equation (3), yielding
is the Schwarzschild radius. An asymptotic expansion for the metric functions can be obtained from Equation (2) and Equation (3), yielding
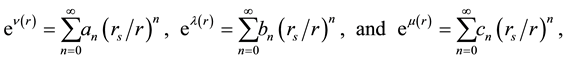 (4)
(4)
where
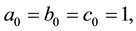 (5)
(5)
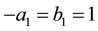 (6)
(6)
and
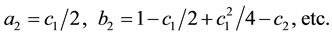 (7)
(7)
It is obvious that 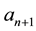 and
and 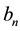 can be expressed as functions of
can be expressed as functions of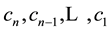 .
.
3. Geodesic Equations and Time Delay Experiment
The geodesic equations can be obtained from variations of the line integral over an invariant parameter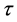 ,
,
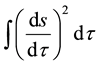 , and their integrals are given by [1] [2]
, and their integrals are given by [1] [2]
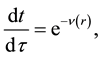 (8)
(8)
where the integration constant for the t variable is chosen to be 1 by fixing the normalization of the  variable. With the integration constant for the
variable. With the integration constant for the 


while with the integration constant for the total angular variables, 

Restricting the plane of motion to 


where E is a constant of integration for the s variable,

and

The constant E is 0 for light propagation.
From Equation (8) and Equation (11) with Equations (5) and (6), it follows that


for light propagation, where 


In fact, the observational data of Shapiro et al. [3] fit well with high degree of accuracy with the formula

The accuracy of the data is 1 in 1000 in the original data and 1 in 105 in more recent data [4] . This is the result also suggested by the PPN (the parametrized post-Newtonian Formalism) [1] . However, this is not a correct result from General Relativity with the Schwarzschild metric, since the geodesic equation yields Equation (16) with 

As a matter of fact, all experimental data fit with the formula of Equation (17). It is worthwhile to mention that the time delay experiment has been extended to a binary pulsar [6] .
We note that the parameter values

are coordinate independent and determined from the solution of the Einstein Equation and the physical boundary condition. Thus we conclude that Equation (18), along with Equation (16), is the condition for the correct metric.
4. The Schwarzschild Metric in 1916
In the so-called Schwarzschild metric,

or

This result, Equation (16), with
In the original form of 1916 article [5] , Schwarzschild proposed the condition

i.e., the same as in vacuum, or

From Equation (2) and Equation (3), one can get

For the asymptotic solution,

or rewriting this equation as

its solution can be expressed as

where 
5. Physical Condition That Fits the Time Delay Experiment
What is the physical condition that leads to the condition of Equation (18)? It comes out from the following ansatz.
Proposition 1 The speed of light in the angular direction in the SSS metric is the same as that of vacuum.
In other words,

in the first order of gravity. This ansatz implies that although gravity deforms the geometry of space-time, speed of light perpendicular to the gravity will not be affected. If this ansatz is extended to any order of gravity, then it will determine all the metric functions exactly and fix the geometry of the physical metric. Recently, time delay experiments were performed for binary pulsars, where an accompanying partner is a compact object such as a neutron star [6] . Obviously, one is coming to a regime of higher order effects of gravity. If one finds an observation of a binary pulsar, where an accompanying partner is a black hole, then one needs information of higher order effects of gravity. In the following sections, the author describes and performs such a task.
6. The Physical Metric in Higher Order
In order to determine the coefficients in higher order, 

Then one gets for the asymptotic solution,

Then one has

or

Differetiating Equation (32), one gets

From Equation (3), the metric function in the radial direction can be calculated

From Equation (31) or Equation (32), it is clear that one covers the range of

and

In order to cover the range of

one has to use non-asymptotic solution of the Schwarzschild solution. From Appendix, such a solution is given in the latter part of this section.
The asymptotic expansion of the metric functions can be calculated from Equation (32) and Equation (34) as

and

Successive expansion yields a determination of all the parameters, cn, for the physical metric. These are useful for testing observational data in higher order in gravity. Alternatively, the inverse function of Equation (31) or Equation (32) may be used.
From the Appendix, the Schwarzschild solution for non-asymptotic region can be written as

and

where A and D are constants. Then, the metric functions for the physical metric in the region

are expressed as

and

and hence

or

Differentiating Equation (45), one gets

and

Imposing the continuity of the asymptotic expression, Equation (31) and the non-asymptotic expression, Equation (45) at

one gets

The most appropriate region in the parameter space is

since the range of coordinate, r, is covered by the origin and the positivity of the metric functions are maintained.
Figure 1 showes the picture of 

In the region of Equation (51), the distance r can be reached at zero when 


Notice that there is an undecided one parameter which can be fixed for the physics inside the horizon at

Figure 1. The metric function, 

7. Time Delay Experiment by a Black Hole
If a time delay experiment of a binary pulsar is performed by a black hole companion, one needs a higher order correction of gravity. From Equation (31) and Equation (33), one gets

Then, using Equation (14) and Equation (34) one gets

and hence the time delay is expressed as

where 


and

Outside of the horizon,

and the time delay 


However, when one reaches at the horizon

one gets

and

Then, the integration of 
This divergence property may be related with the characteristic of the physical metric, in which the horizon,

is, at the same time, a circular radius. This is because the speed of light in the radial direction vanishes at the horizon,

while the speed of light in the spherical direction is that in vacuum for the physical metric.
8. The Other Experimental Tests of General Relativity
The other tests of General Relativity are shown to be insensitive to the presence of the 


Integrating this from a large distance, one gets the well-known expression for the bending of light [2] ,

The integration of the 

For the advancement of perihelia, one uses the formula


where 




Due to the relationship, Equation (7), 

It is remarkable that the 





and

one can see that the relationship

is automatically satisfied.
For the gravitational red shift and the gravitational lensing, one uses the first order of gravity in

Then, both metrics, the Schwarzschild metric and the physical metric, give the same prediction for the all experiments in this section at the present time. However, if future experiments find the higher order effects, such as the gravitational red shift near or inside black holes, then these observations will substantiate the difference between the both metrics. In fact, the gravitational shift inside the horizon in the physical metric is shown to be gravitationally blue shifted.
9. Summary and Discussion
The author has shown that the very accurate data of time delay experiments collected by Shapiro et al. are not explained by the Schwarzschild metric. The physical metric proposed by the author gives the correct description for the data. This changes the nature of gravity inside the horizon. The size of a black hole becomes 2.60 times bigger than the Schwarzschild radius and the gravity inside the horizon shows a repulsive force. Some of these properties will be tested by the observations of the MIT Haystack Observatory. The author has demonstrated that the change of the metric shows the direction of general relativity and points to a new way of understanding the nature of gravity.
Acknowledgements
It is a great pleasure to thank Peter K. Tomozawa, Malia M. Tomozawa and Tai N. Tomozawa for reading the manuscript.
References
- Misner, C.W., Thorne, K.S. and Wheeler, J.A. (1973) Gravitation. Freeman, San Francisco.
- Weinberg, S. (1972) Gravitation and Cosmology. Wiley and Sons, New York.
- Shapiro, I.I., et al. (1966) Physical Review Letters, 17, 933. http://dx.doi.org/10.1103/PhysRevLett.17.933 Resenberg, R.D. and Shapiro, I.I. (1979) Astrophysical Journal, 234, L219. http://dx.doi.org/10.1086/183144
- Bertotti, B., Iess, L. and Tortora, P. (2003) Nature, 425, 374. http://dx.doi.org/10.1038/nature01997
- Schwarzschild, K. (1916) Sitzungsber. Press. Skad. Wiss. Berlin Math. Phys, 189-196.
- Jacoby, B.A., et al. (2003) Astrophysical Journal, 599, L99. http://dx.doi.org/10.1086/381260 Demorest, P.B., et al. (2010) Nature, 467, 1087. http://dx.doi.org/10.1038/nature09466
- Duff, M.J. (1974) DRG, 5, 441. Newman, E. and Goldberg, J.N. (1959) Physical Review, 114, 1391.
Appendix: The Schwarzschild Solution
Setting

in Equation (1), and using the Maple program the Einstein Equation reads


and

From the sum of Equation (78) and Equation (79), one gets

Using this relation, Equation (80) becomes

or equivalently

On the other hand, Equation (78) can be written as

which solution is

and Equation (83) is satisfied, where B is an integration constant. The solution of Equation (81) reads

The asymptotic solution with the boundary condition is given by

On the other hand, the non-asymptotic solution is given by

where A and D are nondimensional integration constants.


