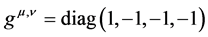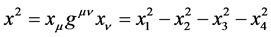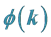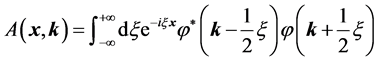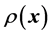Journal of Modern Physics
Vol.05 No.16(2014), Article ID:51066,13 pages
10.4236/jmp.2014.516168
Describe Quantum Mechanics in Dual 4 d Complex Space-Time and the Ontological Basis of Wave Function
Guoqiu Zhao1,2
1Huazhong University of Science & Technology, Wuhan, China
2China Institute of Basic Science of Hubei, Wuhan, China
Email: zhao66@126.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 September 2014; revised 29 September 2014; accepted 18 October 2014
ABSTRACT
Micro-object is both particle and wave, so the traditional Particle Model (mass point model) is actually not applicable for it. Here to describe its motion, we expand the definition of time and space and pick up the spatial degrees of freedom hidden by particle model. We say that micro-object is like a rolling field-matter-ball, which has four degrees of freedom including one surface curvature degree and three mapping degrees in the three-dimensional phenomenal space. All the degrees are described by four curvature coordinate components, namely “k1, k2, k3, k4”, which form the imaginary part of a complex phase space, respectively. While as to the real part, we use “x1, x2, x3, x4” to describe the micro object’s position in our real space. Consequently, we build a Dual 4-dimensional complex phase space whose imaginary part is 4-dimension k space and real part is 4-dimension x space to describe the micro-object’s motion. Furthermore, we say that wave function can describe the information of a field-matter-ball’s rotation & motion and also matter-wave can spread the information of micro-object’s spatial structure & density distribution. Matter-wave and probability-wave can transform to each other though matter-wave is a physical wave. The non-point property is the foundational source of the probability in Quantum Mechanics.
Keywords:
Field-Matter, Matter-Wave, Probability, Curvature, Curvature Coordinate

1. Introduction
De Broglie came up with his assumption that each object has its wave-like characteristics in 1923-1924 by mak- ing an analogy of the wave-particle duality of light, and it was later confirmed by experiments. To explain the wave-particle duality of a micro-object, Schrodinger supposed the motion of a micro-object is like the oscillation of “Elastic Fluid Limited in a Shell”. Using the solution of pressure equation of “Elastic Fluid”, we can get the wave function of a kinetic electron. Then putting it into the pressure equation of “Elastic Fluid”, we will get the Schrodinger wave equation [1] . Schrodinger thought the wave-like nature is more basic than the particle- like nature for a micro-object, and particle is a wave packet composed of waves. The wave function squared is the weight of partition function of the electric charge e. Schrodinger’s assumption was gave up by physicists because of its difficulty in multi-dimensions space and the diffusion of wave packet.
De Broglie assumption: a micro-object corresponds to a wave (vibration) [2] . This model is a mass point model, too. The motion of a mass point corresponds to a matter wave (phase wave) [3] . It can be described that particle is “riding on a wave” and lead by wave to go forward. Later, De Broglie persisted in the “Dual Solution Theory”, namely, the nonlinear solution was in the center and formed the particle, while the plane wave solution was in the outer and guided the particle. However, it’s difficult to understand “the motion of a mass point corresponds to a matter wave (phase wave)” and is too complex to get the nonlinear solution in math. So the De Broglie assumption was not accepted widely.
Then the Copenhagen School gave the uncertainly principle that position and momentum cannot be determined at the same time [4] . A single particle has its volatility, wave-function is a probability-function and the wave function squared equals to the distribution probability. The Copenhagen School is the mainstream thought now, though it has suffered the arguments between the Determinism and Indeterminism, Locality and Non-lo- cality, Realism and Anti-realism for many years until this century [4] .
To explain the determinism fact beyond the probability function, Bohm thought out the “Hidden Variable Theory”. He reformulated the Schrodinger wave equation and loaded it with new significance according with the classical Hamilton Jacobi theory while avoiding the “Von Neumann Argument” [4] . Bohm thought the micro-particle should be treated as a real particle with continuous movement. It can be affected by the classical potential U as well as the quantum potential Q which is related to the wave function and determined by the solution of Schrodinger Equation [5] . Quantum Potential is the main difference between classical theory and quantum theory. Though Bohm had received many agreements, he failed to challenge the predominant Copenhagen School in Quantum Mechanics because of the unclear of the quantum potential in physics.
Many-worlds interpretation: different measurements correspond to different world. We step into a different parallel world when we measure it once, twice and so on. The world we are in now is the result we have stepped into before. World has infinitely many sliders. However, we can only in one at a time. The real world can never collapse and the real collapse is the many worlds in our mind collapse into the real world we are in. In fact, the Many-worlds interpretation cannot eliminate the collapse, it just shift the place of collapse. So it is more like a category in philosophy.
Sakata Shyoichi (Japanese), yukawa hideki (Japanese) and Tohm (French) both think the main difficulty in Quantum Mechanics comes from the unreasonable mass point model [5] [6] . String theory is a beautiful non- point theory which has satisfying results in the combination of general relativity and quantum mechanics. But it is really an unverifiable conjecture that string is the basic cell for the whole world. What we need is verifiable. Considering of the success in combination of unifying gravity and quantum mechanics, the Ring theory is another wonderful theory who can match the String theory. However, it is even more difficult to be understood because of its nets and conjunctions are really hard.
The fowling rotating flied-matter-ball model may be able to solve the difficulties in Quantum Mechanics. For example, we can know the ontological foundations of the matter-wave by deducing the wave function [7] . Field- matter is the basic form of matter. The structure of field-matter-ball consists of the rotation radius, frequency, and matter density distribution. We argue the field-matter-ball model is a proper model for micro-object and can satisfy the wave-particle dualism at the same time. But it must be pointed that the matter-field-ball is not the same as the classical ball we see in our world, and it is a “quantum ball” which has its only intrinsic quantities.
Each model is based on its original assumption. Point, String, Ring and Field-Matter-Ball model are the same on this point. They are all based on its foundational assumption and they are equal to some degree because there is no priority level among the models. When we judge a model is good or not, the key point is whether the model is handy to help us to well understand something or not. Concise is the basic requirement in Physics. The main defect in Physics now is not the short of methods in math, actually is the over excess of math.
Smolin (One of the founder of the Ring theory) had said in “The trouble with Physics” like this: there is an insurmountable difficulty in Point modeling, String theory and Ring theory. He expected a combination of the Quantum mechanics and general relativity by some new thought on the intrinsic quality of the space-time [8] . Complex number is used in space-time is exactly a new breakthrough. On one hand, it is convenience we use a field-matter-ball model to describe the quantum phenomenon. On the other hand, we are talking a Dual 4-di- mensional complex space not an 11-dimensions or 26-dimensions space or even higher dimensions space which are unimaginative.
The Dual 4-dimensional complex space description can cover all quantum phenomena now, and it can have a clear connection with Gravitational Field. The flowing work is to integrate the Quantum Mechanics, Space-time and Gravitation. We expect we can offer a new direction to make breakthrough in Physics.
2. Some Physical Concepts
2.1. Micro-Object
To avoid the trouble caused by mass point model, we call the micro particle as micro-object.
2.2. Some Concepts
1) Static micro-object Compton momentum: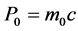 , where m0 is the static mass;
, where m0 is the static mass;
2) Kinetic micro-object Compton momentum: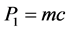 , where m is the kinetic mass;
, where m is the kinetic mass;
3) The relativistic momentum:  (i = 2, 3, 4), where c is the light velocity;
(i = 2, 3, 4), where c is the light velocity;
4) Static micro-object Compton wavelength: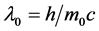 , where h is the Planck constant;
, where h is the Planck constant;
5) Kinetic micro-object Compton wavelength: ;
;
6) Micro-object De Broglie wavelength: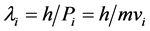 ;
;
7) Eigen Radius of static micro-object: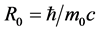 ; Eigen Curvature of static micro-object:
; Eigen Curvature of static micro-object: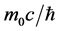
 ;
;
8) Eigen Radius of kinetic micro-object: ; Eigen Curvature of kinetic micro-object:
; Eigen Curvature of kinetic micro-object: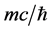
 ;
;
9) Radius 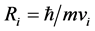 and Curvature
and Curvature . These two are the mapping of micro-object R0 in three dimension phenomenon space. They are the main study objects in Quantum Mechanics.
. These two are the mapping of micro-object R0 in three dimension phenomenon space. They are the main study objects in Quantum Mechanics.
Notes: the subscript “0’ represents the static micro-object’s property. The subscript “1, 2, 3, 4” represents the kinetic micro-object’s properties. The subscript “i” represents some physical quantity in the three-dimension phenomenon space.
2.3. The Relationship between the Relativistic Energy Momentum and Curvature
If m and m0 is the micro-object’s kinetic mass and static mass, using the relativistic energy equation 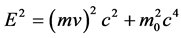 and
and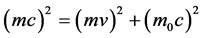 .
.
Then we can get 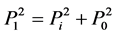


Here we have such vectors: p1, pi, P0, k1, ki, K0. k1 − ki = K0, k1 and ki can construct a 4-dimension Curvature coordinate associated with kinetic micro-object’s motion.
3. Geometry of a Micro-Object
3.1. Micro-Object Is Like a “Rolling Field-Matter-Ball”
1) For static state,
Curvature Radius:
which represents the field extension in a micro-object.
Curvature: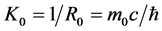
which represents the camber of micro-object’s surface.
2) For kinetic state,
Curvature Radius: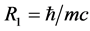

Curvature:
where m is the kinetic mass. And the faster the object is moving, the larger the kinetic mass is, the smaller the Radius is and the larger the Curvature is [9] . It is easy to know:

3) For mapping in three-dimension phenomenon space,
Radius:
where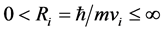
Curvature: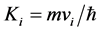
where 
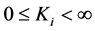
4) For rotational frequency,
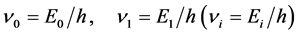
where


5) For density of the field-matter,

where V is the volume of the field-matter-ball. V is function of Curvature K because of

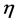


3.2. The Hidden Degrees of Freedom by Particle Model
The curvature components K1 and 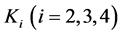


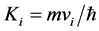
The Radius and Curvature of a micro-object represent the state of its motion. R0 and K0 are not observable in our 3-dimension phenomenon space. It is the ontology of itself. While Ri and Ki is visible. R1 and K1 is like a bridge between noumenal world and phenomenon world (the same as light cone). If R0 and K0 do not exist, Ri and Ki, R1 and K1 won’t exist, too. R0 and K0 is the foundational source of every physical phenomenon.
The change of Radius R (or Curvature K) will surely bring the change of distribution in field-matter-ball, thus will help us to deeply understand the ontology of wave function.
3.3. Describe of the Field-Matter-Ball
1) In coordinate complex space,
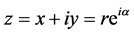
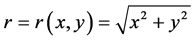
If the modulus of the complex number r is defined by Curvature Radius R, then the above-mentioned coordinate becomes into a field-matter-ball’s spherical coordinate,

For static micro-object: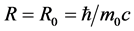
For kinetic micro-object:
For mapping in three-dimension space
2) In curvature complex space,
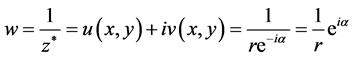
where w is mapping space of z, describing a spherical coordinate whose modulus is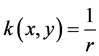

For static micro-object: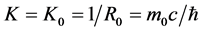
For kinetic micro-object:
For mapping in three-dimension space
In z space, matter-wave-field is in, and the outer in empty, thus it can be simply treated as a mass point under the large scale. In mapping space w, matter-wave-field is out of the ball by mapping, and the inner is empty. For field-matter-ball, z space and w space are mapping to each other, describing the same thing.
In real time and space, we describe the motion or the probability by mass point model. While in complex space, we use Curvature Radius or Curvature. And this is the physical significance why micro-object does not have orbital motion.
Curvature K is an expansion of the wave number k, geometry of a micro-object, indication of the hidden degrees of freedom by mass point model.
The movement of matter-wave-field has something to do with the interaction of a micro-object.
4. Matter-Wave and Phase Space
4.1. How to Generate the Matter-Wave and Wave Function
The rotation of field-matter can be written as
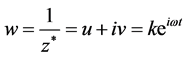
where 
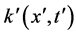

where
Suppose the 
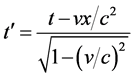

where 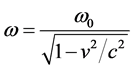
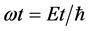
Function (16) is just the wave function in Quantum Mechanics. So the intrinsic property of matter-wave is field-matter’s rotation. For free micro-object, A is normalization constant.
The deduction of matter-wave can at least solve the following questions:
1) Can ensure that it is harmonic with traditional Quantum Mechanics, such as the assumption of energy, frequency, momentum and wavelength, without increasing any new assumption.
2) Can uncover the mysteries of Quantum Mechanics wave-function. Because we can see that matter-wave is the real propagation of physical wave, and it is not an assumption or a thought.
3) Can unify the Quantum Mechanics and the theory of relativity in logic foundation, also can support the assumption that wave function is continuous field in quantum field theory.
4) Prompt us to find the internal relation between matter-wave function and probability function.
4.2. Schrodinger Equation and Dirac Equation
If we treat Equation (16) as a complex description of field-matter-ball by observe system and take no account of its phase, phase space, the physical relationship between field-matter-ball and its motion ,and the physical significance, then we can get Dirac equation by using Dirac operator. Thereby, this theory system is conform to the
relativistic Quantum Mechanics’ rule. When 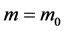
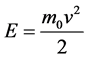
lativistic Quantum Mechanics, namely, the nonrelativistic Quantum Mechanics wave function. Using Schrodinger operator, we can get the Schrodinger equation, and it is conform to the nonrelativistic Quantum Mechanics’ rule [9] . Using the Klein-Gordon operator, we can get the Klein-Gordon equation. But now we take no consider of the rotation vector effect of the matter-field-ball, so it is a relativistic scalar matter-field. Consequently, Schrodinger equation and Dirac equation are not assumptions, but the motion equation generated by using mathematical methods in real matter-wave function.
5. Phase Space of Wave Function
In fact, the phase space of wave function has a specific physical significance when we take the field-matter-ball model into account. Wave function will present the change of a micro-object’s spatial structure in Dual 4-di- mension complex phase space
So
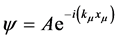
where 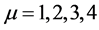
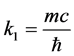

The phase angle is function of 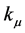


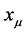
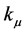
The phase space demonstrates that there are hidden degrees of freedom by Particle Model in traditional Quantum Mechanics. It has a direct relationship with the motion state of a field-matter-ball and the observer system, too.
1) 
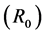
2) 
micro-object R0 on the Light Cone surface.
3) The rotation of itself and the motion all have reflections in the phase and the matter-wave 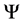
6. The Dual 4-Dimension Complex Phase Space
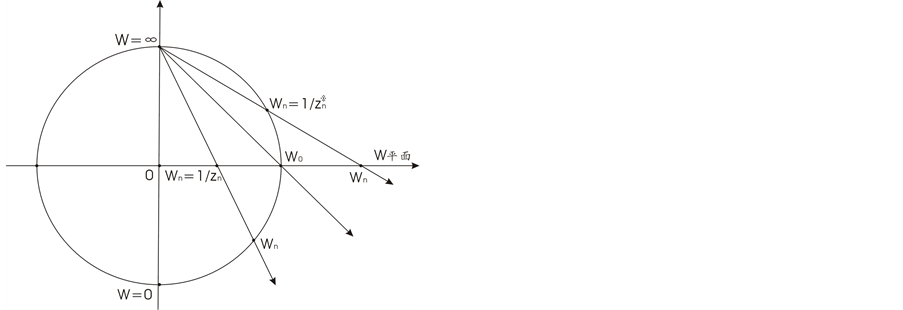
6.1. Sphere of Complex Numbers
The wave function is formed from the rotation and motion and is a function in Dual 4-dimension complex phase space. Plural can be defined on the plural ball [11] . See Figure 1.
Complex number can be defined by a sphere of complex numbers.


Figure 1. The plural ball-Riemannian ball.
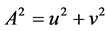
Suppose

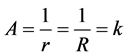
1) In complex number


when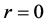
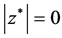
2) The curvature:
When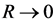

When
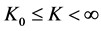
3) The significance of the mapping from internal to external.
From Dual 4-dimension complex phase space to the 4-dimension real time and space, a micro-object’s k- space will be compacted into zero-dimension space by
6.2. The Dual 4-Dimension Complex Phase Space
6.2.1. The Dual Quaternions Complex Space
Set 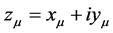
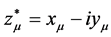
Wave function 
6.2.2. The Dual 4-Dimension Complex Phase Space
The Dual 4-dimension complex phase space comes from the Dual 4-dimension complex number 


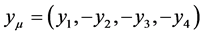

Wave function 
(21-2) is a function defined in a complex phase space. Though the function is completely the same as (21-1), 

6.2.3. Matter-Wave in Complex Phase Space
Set y = k, namely,



Wave function 
Actually, this is the Equation (17).
Using the position vector X and Curvature vector K, we get a Dual 4-dimension complex phase space

Generally we call a Quantum Mechanical wave function phase space mathematical space. We can differ that the micro-object is in a complex space. When we observe it, it will automatically come into being a real physical space we call Dual 4-dimension complex time and space.
It must be pointed that, the position complex space 
They can convert to each other by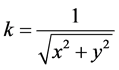
complex phase space 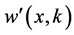
The metric tensor of 
k and 
7. The Matter-Wave Differential Function
In Dual 4-dimension complex space, the wave function must be analytic.
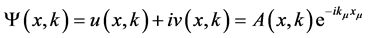
The real part and imaginary part should satisfy the Cauchy-Reimam conditions
The amplitude is
Set y = k, we can get the matter-wave-function described in Dual 4-dimension complex phase space:
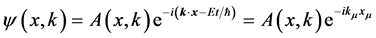




where 
Moyal product rule:
The average value of a physical quantity 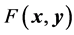

The wavelength of a system can be defined by general De Broglie wavelength.
8. The Relationship of Wave Function 
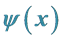
The point (x, k) in Dual 4-dimension complex phase space can be explained as follows: 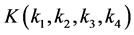

8.1.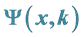

The micro-object described in Dual 4-dimension complex space, shows its extension in K space and position in x space. As to the wave-particle duality, it can be confirmed by the mapping from the wave function in Dual 4-dimension complex space to the probability in real 4-dimension space and time.
It has been proved that, the wave function
is a matter-wave function in Dual 4-dimension complex space. The amplitude 
The micro-object’s motion satisfies the Dirac equation (or Schrodinger equation). And it has a relationship with 
For the two integral operations
1) Eliminating the variable k, then the amplitude 

where the normalization is
2) Eliminating the variable x, then 

where the normalization is
3) 

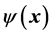
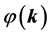
Now let us talk something about the point x (and its neighborhood):
1) when k is common: the larger ρ the larger η and the smaller ρ the smaller 


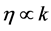
We can make an intuitive understanding that we get the information of the probability density distribution from the matter-field density distribution. Where there is a higher distribution of matter-field density, where there is a higher distribution of probability density .They have a positive correlation.
Based on this, the sphere model and the particle model or the η description and the ρ description can make sense: for a micro-object, when the volume is smaller, field-matter density η will become larger, so the probability of it can appear in the ball as a particle is larger. When the volume becomes larger, it goes to the opposite result. V = ∞, η = 0, ρ = 0, V = 0 (mass point), η = ∞, ρ = 1 (δ function). The η description and the ρ description are actually equivalent while η is small scale space description and ρ is large scale space description.
Discussion:
1) The matter-field density has a uniform distribution in large scale, so is the probability distribution of where the micro-object would occur. If the distribution was not uniform, the probability would be large in the places where the density is large.
2) For free micro-object, the density is uniform. The matter-field density η and the probability density ρ in unit volume are both an average value. If the scale was smaller than the Radius scale R, the average η and ρ had no definition. The reason why we define the η and ρ both in a sphere with a Radius R is that there is an equivalency between the matter-field density η and the probability density ρ.
3) When


the spinor wave function in Quantum Mechanics.
4) k0 is independent of position and existing in vacuum space. Also, it is described in Curvature space. k0 represents the high frequency vibration and is source of the probability [13] .
5) The uncertainly of position is because of the size of a micro-object (Compton wavelength)
8.2. Wave Function, Eigen State and Eigen Value
The wave function 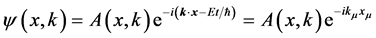
For stationary state wave function:
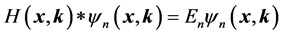
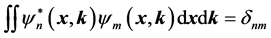
The modular square of the decomposition coefficient is the probability of finding an eigen state in some place. Before measuring, the wave function is in the Dual 4-dimension complex phase space .while after measuring, it is collapsed in real space. Measurement contains the transformation of space to describe and the corresponding experiment values. Measurement will have a new connotation in our new theory, and we will discuss it in another article.
The eigen states of an atom is non-continuous so that the energy band in E-k space will have corresponding energy states. With the decrease of the energy gap, the energy will become continuous. Then the Hilbert space will be useful.
Discussion:
1) When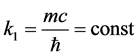

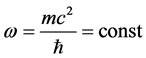
tude
2) When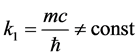

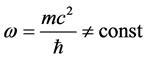
the spin and the energy will change, too.
a) To increase the frequency, the micro-object will speed up absorbing energy and transiting to higher energy state.
b) To decrease the frequency, the micro-object will slow down releasing energy and transiting to lower energy state
a) and b) are both breaking down to the stationary state, and we call them stimulated and de-stimulated, respectively. Wave function becomes a function of time. By absorbing or releasing energy, electron transit from one energy state to another. The generation or annihilation of a particle in quantum field theory is transition actually. The observe system we use in the derivation of the wave function is a corresponding quantum transition in Dual 4-dimension complex space. To solve the specific quantum transition and take the interaction time into account, we can use time-dependent Schrodinger equation or Heisenberg equation.
3) Every single static stable micro-object has standing wavelength. For uniform motion, the standing wavelength is. For non-uniform motion, the wavelength is changing and the original stable condition is broken down, thus causing the radiation, until the new stable state come into being.
4) There are no two different states at the same time and the electron energy emission in transition is one by one (photon). The change of energy is a sudden change and do not need time if neglecting the interaction process. This will provide a physical foundation of the discontinuity of eigenvalues or eigenstates which come from the wave function operated by an operator.
The confusing phenomenon that there are different probabilities in different eigen states of a micro-object is deeply hidden in the mathematical property. “Existing at the same time” is not a real physical process but a derivative feature from physics to math caused by the sudden change of energy state. The noumenon can never be observed, what we have seen is the phenomenon [9] [14] and what can “Existing at the same time” is phenomenon.
9. Experiments Evidence on Particle Radius
9.1. Hofstadter’s Particle Radius Experiments
Using the 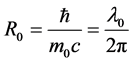

We can see the theoretical value and the experimental value are very close (Table 1).
The micro-object is not a mass point. It has its spatial distribution and the Radius will decrease when the velocity increases. It is reasonable we use Compton wavelength to describe as the micro-object’s Radius in extension.
9.2. The Landau Uncertain Property of a Single Mechanical Quantity
Actually, Landau had an explanation [16] on m0c in 1930. He said, when measuring a single mechanic quantity, the uncertainty of position is 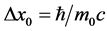
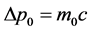

Electron is not a mass point, and it has its real Radius where it distributes in. If we treat an electron as a point, it must be in the size R0. The size of the electron R0 becomes the range an electron point can reach. We cannot have a clearer knowledge about where is the electron smaller than R0. So we have recognition of the uncertainty of position. This is an important theoretical foundation what Landau had provided for the non-point model.
10. Conclusions
1) When observing a micro-object in a macro large scale condition, the micro-object can be simply treated as a mass point (h ® 0, R ® 0). It has a certain geometric coordinate and can be described completely and clearly in 4-dimension real space. However, when observing it in a micro condition, the micro-object itself is a rotating field-matter-ball. We have to recover the hidden degrees of freedom and it would never be taken as a mass point.
2) We have known, the matter-wave carries the information of the structure and the field density of the micro- object. The rotation and motion of either charged particles or uncharged particles will spread the matter-wave. So people can use it in communication science.
3) We should have new understanding of the five basic assumptions in Quantum Mechanics. Matter-wave and probability-wave can convert to each other.
Table 1. Radius of electrons, protons and neutrons experimental value compared with the theoretical value Compton wavelengths (static—R0, move—R1).
4) We construct a Dual 4-dimension complex space for Quantum Mechanics from the vector (x, K) to describe the movement of a micro-object. The static ones are in coordinate complex space, while the kinetic or matter-waves are in Dual 4-dimension complex space.
5) Matter-wave may be the source of the whole Quantum Mechanics.
6) The field-matter-ball model is in keeping with the ring current model for electron by Dirac [17] . We will calculate the Bohr magneton, the spin magnetic moment of electron, the nuclear magneton, the proton magneton and the neutron magneton accurately in supplement
Acknowledgement
Thanks a lot for many scholars and professors domestic or abroad. They have given many concerns or guidance on this project for a long time. Some have participated in the conference discussion and some have cooperated in publishing papers. Here are our sincere thanks for all of you.
References
- Fan, D.N. and Hu, X.H. (2007) Schrodinger: Schrodinger’s Lectures. Peking University Press, Beijing, 8, 9, 12.
- (2004) L. de Broglie on the Theory of Quanta. Annales de Physique 10e serie t.3 (Janvier-Fevrier) 1925. Translated by A. F. Kraklauer.
- Huang, H.Q. (1979) Myth of Quantum Mechanics. Science Press, Beijing.
- Qin, K.C. (1989) The Philosophy of Quantum Mechanics. The Commercial Press, Beijing, 67-99.
- An, D. (2001) Sakata Shyoichi Proceedings of a Philosophy of Science. Shanghai Translation Publishing House, Shang- hai.
- Zhou, Z.L. (1989) Mutation Theory, Thoughts and Application. Shanghai Translation Publishing House, Shanghai.
- Zhao, G.Q. (2013) Curvature Interpretation of Quantum Mechanics on the Outline.
- Smolin, L. (2008) The Trouble with Physics. Translated by Yong Li. Hunan Science and Technology Press, Changsha.
- Zhao, G.Q. (2008) From the Interaction to the Newly Issued Curvature Interpretation of Quantum Mechanics.
- Bjorken, A.D., et al. (1984) Relativistic Quantum Mechanics. Beijing Science Press, Beijing.
- Cao, T.Y. (2012) Quantum Mechanics Foundation International Research and Curvature Explanation Workshop Report.
- Li, K., Wang, J.H., Dulat, S. and Ma, K. (2010) International Journal of Theoretical Physics, 49, 134-143.
- Quantum (2012) Cai Gen Tan. Tsinghua University Press, Beijing.
- Cao, T.Y. (2010) From Current Algebra to Quantum Chromodynamics: A Case for Structural Realism. Cambridge University Press, Cambridge, 202-241.
- Ye, Y. and He, X.S. (1981) Feynman Physics. Science Press, Beijing.
- Zhang, Z.J. (1997) Relativistic Physics. Central China Normal University Press, Wuhan.
- Yang, F.J. (1979) The Physics in 20th Century. Beijing Science Press, Beijing.
Supplement
1.1. Field-Matter-Ball Model for Electron
Spin radius:

Spin frequency:

Spin period:
Current:
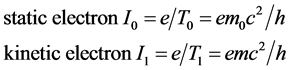
1.2. The Electron Magnetic Moment
1.2.1. Static Electron

The spin magnetic moment of electron is equal to Bohr Magnetron.
1.2.2. Kinetic Electron

So the kinetic electron magnetic moment will decrease as the velocity increase.
1.2.3. Nuclear Magneton and Proton Magneton
For nuclear magneton:

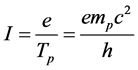
Set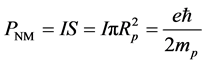



The spin magnetic moment of up quark is
The spin magnetic moment of down quark is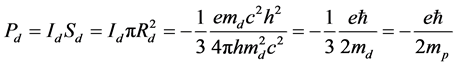
So the magnetic moment of proton: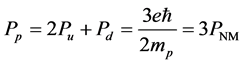
But this theory result is quite different from the experiment result. We can rewrite the magnetic moment of proton like that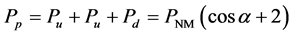

When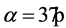

It must be pointed that, quark cannot be directly observed. So the magnetic angle assumption has no contradiction with the fact. And it is the result after we have considered all the interactions in micro field. In spite of the inequality of the mass between the up quark and the down quark, we can adjust the angle to make sense and make it equal to the experiment results. The magnetic angle assumption is general applicable. The correspondence between the angle and spin magnetic moment in experiment is just like the correspondence between eigenstate and eigenvalue.
1.2.4. Neutron Magneton
If the up quark is anti-parallel to the two down quarks, then
While in fact the magnetic moment of neutron is not 0, the condition is wrong.
Adjusting the angle
So the value is negative.
If the mass of up and down quark is not equal, by adjusting the angle, we can make the theory value and the experiment value exactly match.
We are looking forward to the experimental physicists’ work.